3.3有理数的乘方(1)

有理数的运算（3）——有理数的乘方（一）【教材解读】1、有理数的乘方的意义和法则2、有理数的乘方的运算及其混合运算 【知识点解释及题讲精讲】1、有理数的乘方的意义 口算222⨯⨯= (-3)(-3)(-3)(-3)⨯⨯⨯= ●1111144444⨯⨯⨯⨯= 归纳：若a a n aa ⋅=n 个读作a 的几次方乘方的意义：求几个相同因数积的运算叫乘方；乘方的结果叫做幂。

书写时注意： 1）、指数写在底数的右上角2）、当底数为负数或者是分数要加上括号如： 223(3)--与 223344⎛⎫ ⎪⎝⎭与它们的意义不同，读法也不同。

例1 填空 内容 数目意义 读作 底数 指数 幂 24（-2）4（-3）5 -34334⎛⎫- ⎪⎝⎭334-例2 填空、计算 内容 数目幂 底数的正负幂的正负2341()2（2×3）2（-3）2n a 底数指数 幂0321()4- 31()5-例3利用乘方的定义计算321(3)()2-⨯- 233228----+● 320(3)3(2)--÷⨯- ❍23211(2)(3)6⎡⎤--⨯-+-⎣⎦例4 已知420082008200820081(1)()(1)(2)()b o a b a++=--+-+a-2求3、科学记数法在目前所学的范围内例如：10(110,)n a a n ⨯≤<为正整数的形式表示数叫科学记数法 例5、 用科学记数法表示下列各数314160000= ，-1060000= 1050000000= ，-27010000= 例6、 求下列各数的原数107= 3×107= 3.14×102= -3.612×105= 观察原数Q 的整数位与n 之间有怎样的关系？ 【巩固练习】一、选择题1、下列各数中运算后的结果相等的是（ ）A 43与 34B 335(5)-⨯-与C 22(6)6-⨯-与D 225225⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭与2、 下列说法正确的是（ ）A 23表示 23⨯的积 B 任何一个有理数的偶数次幂是正数 C 223(3)--与互为相反数 D 负数的任何次幂都得负数 3、计算115()555⨯÷-⨯的质量（ ）A -1B -25C 25D 04、据报道2007年全国高考报名总人数约为9500000人，今年高考人数比2007增加5%用科学记数法可表示为（ ）A 0.9975×107B 9.9975×107C 9.9975×106D 99.975×106二、 填空题1、537⎛⎫- ⎪⎝⎭中，底数是 指数为2、若2007y 23x-3+(y+1)=0 则(-x)=3、003200412(1-)+(-)= 4223721⨯2-(-)-(-)=4、按下列程序进行计算，当输入值为20时，则输出结果为 三、计算22422326(1)(3)(1)3-⨯+-⨯- 2331313(-)2()2⨯-÷-【课外作业】一、选择题1、下各组数中，相等的有（ ）对-52有（-5）2-3）3与-33● (-0.3）5与0.35❍ 0100与0200⏹ （-17）3与（-1）2A 1B 2C 3D 42、已知 01,a <<⋅⋅21则-a -a -的大小关系是a（ ） A <-<21-a a -a B <-<21-a a -a C <-<21-a -a a D <<-21--a a a3、计算 2223(23)⨯--⨯-的值是（ ） A 0 B -54 C -27 D -184、 对（-3）4的说清正确的是( )A 读作负的3的四次方B 底数是3，指数是4C 底数是-3，幂是81D 底数是-3，4是幂 二、填空题 1、平方后等于49的数是 ，立方后等于-64的数是 2、我国幅员辽阔，南北相距约5500KM ，用科学记数法表示为 _____________ 3、若[]230(1)(2)(3)x y x y δδ+++-=+-+-1则= _________输入 12⨯211()2⎡⎤÷--⎢⎥⎣⎦100>是输出 传上否4、计算22(4)()7-⨯-= ______ 三、计算题223213(2)(2)-22-+---+ 32232112(3)28.5(2)(-)42⎡⎤-+--⨯--÷⎢⎥⎣⎦610四、 观察与探究：1、在数学活动中，小明为了求2341111122222+++++n的值，设计如图@所示的几何图形。

第3讲有理数的乘除及乘方中考内容中考要求A B C有理数的运算理解有理数的运算律；理解乘方的意义掌握有理数的加、减、乘、除、乘方及简单的混合运算（以三步以内为主）运用运算律简化运算；运用有理数的运算解决简单问题科学记数法和近似数会用科学记数法表示数；了解近似数；会按实际问题的要求对结果取近似值中考大纲知识网络图3.1有理数的乘法一． 有理数的乘法1. 有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘．任何数同0相乘，都得0．2. 有理数乘法的运算步骤：先确定积的符号，再确定积的绝对值．3. 有理数乘法的应用：要得到一个数的相反数，只要将它乘1-．4. 多个有理数相乘：（1）几个不是0的数相乘，负因数的个数是偶数时，积为正数；负因数的个数是奇数时，积为负数，即“奇负偶正”．（2）几个数相乘，如果其中有因数为0，那么积等于0． 5. 有理数乘法运算律：（1）乘法交换律：一般地，有理数乘法中，两个数相乘，交换因数的位置，积相等．ab ba =（2）乘法结合律：一般地，有理数乘法中，三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等．()()ab c a bc =（3）分配律：一般地，有理数乘法中，一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加．()a b c ab ac +=+二． 倒数1． 倒数的概念：乘积是1的两个数互为倒数． （1）倒数是成对出现的，单独一个数不能称为倒数．（2）互为倒数的两个数的乘积一定是1，即a ，b 互为倒数，则1a b ⨯=；反之亦然． （3）0没有倒数．2． 求一个非零有理数的倒数，把它的分子和分母颠倒位置即可． （1）非零整数可以看作分母为1的分数； （2）带分数一定要先化成假分数之后再求倒数．知识概述【例】（2017秋•顺义区期末）四个互不相等的整数的积为4，那么这四个数的和是（ ） A ．0 B ．6C ．﹣2D ．2【练习】（2017秋•蓬溪县期末）如果a +b ＜0，并且ab ＞0，那么（ ） A ．a ＜0，b ＜0 B ．a ＞0，b ＞0 C ．a ＜0，b ＞0 D ．a ＞0，b ＜0【例】（2016秋•芝罘区期末）已知abc ＞0，a ＞c ，ac ＜0，下列结论正确的是（ ） A ．a ＜0，b ＜0，c ＞0 B ．a ＞0，b ＞0，c ＜0 C ．a ＞0，b ＜0，c ＜0 D ．a ＜0，b ＞0，c ＞0【例】（2017秋•滨海新区期末）对于有理数a 、b ，如果ab ＜0，a +b ＜0．则下列各式成立的是（ ）A ．a ＜0，b ＜0B ．a ＞0，b ＜0且|b |＜aC ．a ＜0，b ＞0且|a |＜bD ．a ＞0，b ＜0且|b |＞a3.2有理数的除法一．有理数的除法1. 有理数除法法则：（1）除以一个不等于0的数，等于乘这个数的倒数．小试牛刀再接再厉总述思考：多个不是的数相乘，先做哪一步，再做哪一步？知识概述1a b a b÷=⋅，(0b ≠)（2）法则的另一说法：两数相除，同号得正，异号得负，并把绝对值相除．0除以任何一个不等于0的数，都得0．2. 有理数除法的运算步骤：先将除法换成乘法，然后确定积的符号，最后求出结果．3. 分数：分数可以理解为分子除以分母．二．有理数的乘除混合运算先将除法换成乘法，然后确定积的符号，最后求出结果． 注意：乘除混合运算要“从左到右”运算．【例】（2017秋•临沂月考）若x=（﹣1.125）×÷（﹣）×，则x 的倒数是（ ） A ．1 B ．﹣1 C ．±1 D ．2【练习】（2017秋•郯城县月考）÷（﹣10）×（﹣）÷（﹣）【例】（2017秋•昌平区期末）计算：（﹣3）×6÷（﹣2）×．【练习】（2017秋•安图县期末）÷（﹣1）×．【例】（2017秋•怀柔区期末）计算：3×（﹣）÷（﹣1）．5．（2017秋•城关区校级期中）计算： （1）﹣5÷（﹣1）；（2）（﹣）÷（﹣）÷（﹣1）．小试牛刀再接再厉3.3有理数的乘方一． 有理数的乘方1. 乘方的概念：求n 个相同因数的积的运算叫做乘方，乘方的结果叫做幂．（1）一般地，n 个相同的因数a 相乘，即n a a a a⋅⋅⋅⋅⋅⋅⋅个，记作，读作“a 的n 次方”；（2）在中，a 叫做底数，n 叫做指数；（3）当看作a 的n 次方的结果时，读作a 的n 次幂． 注意：()224-=，其底数为()2-，()()()22224-=-⨯-=；224-=-，其底数为2，()()222121224-=-⨯=-⨯⨯=-；239=749⎛⎫⎪⎝⎭，其底数为37，2333977749⎛⎫=⨯= ⎪⎝⎭； 239=77，其底数为3，23339777⨯==； 221391224⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，带分数的乘方运算，一定要先化成假分数后再运算．2. 一个数可以看作这个数本身的一次方，例如，5就是15，指数1通常省略不写．3. 幂的正负规律：（1）负数的奇次幂是负数，负数的偶次幂是正数，即“奇负偶正”； （2）正数的任何次幂都是正数； （3）0的任何正整数次幂都是0． 二． 科学记数法n a n a n a 总述思考：加减乘除混合运算的运算顺序是什么？知识概述1． 科学记数法：把一个大于10的数表示成10n a ⨯的形式（其中110a ≤<，n 是正整数）．2． 用科学记数法表示一个n 位整数，其中10的指数是1n -，10的指数比整数的位数少1． 3． 万410=，亿810= 三．近似数1． 准确数：表示实际数量的数．2． 近似数：在一定程度上反映被考察量的大小，能说明实际问题的意义，与准确数非常地接近．3． 精确度：表示近似数与准确数的接近程度． 4． 精确度的类型： （1）纯数字类按四舍五入法对圆周率π取近似数时 3π≈（精确到个位）3.1π≈（精确到十分位，或叫精确到0.1）3.14π≈（精确到百分位，或叫精确到0.01） 3.142π≈（精确到千分位，或叫精确到0.001）（2）带单位类近似数2.6万（精确到千位） （3）科学记数法类近似数43.5110⨯（精确到百位）【例】（2018•金牛区校级模拟）下列各数|﹣2|，﹣（﹣2）2，﹣（﹣2），（﹣2）3中，负数的个数有（）A ．1个B ．2个C ．3个D ．4个【练习】（2018•河北二模）下列各对数中，数值相等的是（ ） A ．+32与+22 B ．﹣23与（﹣2）3 C ．﹣32与（﹣3）2 D ．3×22与（3×2）2小试牛刀再接再厉【练习】（2018•绵阳）四川省公布了2017年经济数据GDP排行榜，绵阳市排名全省第二，GDP总量为2075亿元，将2075亿用科学记数法表示为（）A．0.2075×1012B．2.075×1011C．20.75×1010D．2.075×1012【例】（2018•绍兴）绿水青山就是金山银山，为了创造良好的生态生活环境，浙江省2017年清理河湖库塘淤泥约116 000 000方，数字116 000 000用科学记数法可以表示为（）A．1.16×109B．1.16×108C．1.16×107D．0.116×109【例】（2016秋•吴中区期末）阅读下列各式：（a•b）2=a2b2，（a•b）3=a3b3，（a•b）4=a4b4…回答下列三个问题：（1）验证：（2×）100=____，2100×（）100=_____；（2）通过上述验证，归纳得出：（a•b）n=_____；（abc）n=______．（3）请应用上述性质计算：（﹣0.125）2017×22016×42015．总述总结：“奇负偶正”你了解全了吗？3.4有理数的混合运算知识概述一．有理数混合运算顺序：1.先乘方，再乘除，最后加减；2. 同级运算，从左到右进行；3. 如有括号，先做括号内的运算，按小括号、中括号、大括号的顺序依次进行． 二． 进行有理数混合运算时的易错点：1. 乘方概念错误，如326=等．2. 底数错误，如2(2)4-=-，224-=等．3. 运算顺序发生错误，如1232123÷⨯=÷=等．4. 分配律运算错误，如112(2)22241522-⨯-=-⨯-⨯=--=-等．【例】（2017秋•招远市期末）形如的式子叫做二阶行列式，其运算法则用公式表示为=xn ﹣ym ，依此法则计算的结果为（ ）A ．17B ．﹣17C ．1D ．﹣1【练习】（2017秋•费县期末）现定义一种新运算“*”，规定a*b=ab +a ﹣b ，如1*3=1×3+1﹣3，则（﹣2*3）*5等于（ ） A ．71 B ．47 C ．﹣47 D ．﹣71【例】（2017秋•揭西县期末）计算：（﹣2）2÷×（﹣2）﹣=______．【练习】（2017秋•河口区期末）计算8﹣23÷的值为_____．【例】（2017秋•泸县期末）计算：﹣14﹣×[2﹣（﹣3）2]．小试牛刀再接再厉【例】（2018•杭州二模）计算：﹣23+6÷3×圆圆同学的计算过程如下：原式=﹣6+6÷2=0÷2=0请你判断圆圆的计算过程是否正确，若不正确，请你写出正确的计算过程．【练习】（2018•邵阳县模拟）计算：﹣14+16÷（﹣2）3×|﹣3﹣1|．【巩固】（2017秋•贵阳期末）计算：（1）1﹣43×（﹣）（2）7×2.6+7×1.5﹣4.1×8．。

浙教版数学七年级上册2.5《有理数的乘方》（第1课时）教学设计一. 教材分析《有理数的乘方》是浙教版数学七年级上册第2.5节的内容，主要介绍了有理数的乘方概念、性质及运算法则。

这部分内容是学生学习数学的基础，对于培养学生的逻辑思维和抽象思维能力具有重要意义。

本节内容与现实生活紧密相连，有利于激发学生的学习兴趣。

二. 学情分析七年级的学生已具备一定的数学基础，掌握了有理数的加减乘除运算。

但学生对于乘方的概念和性质可能较为抽象，需要通过具体的例子和实际操作来理解和掌握。

此外，学生的学习习惯和思维方式各有不同，需要教师在教学中善于引导和调动学生的积极性。

三. 教学目标1.理解有理数的乘方概念，掌握有理数乘方的性质和运算法则。

2.能够运用乘方知识解决实际问题，提高学生的数学应用能力。

3.培养学生的逻辑思维和抽象思维能力，提高学生的数学素养。

4.激发学生学习数学的兴趣，养成良好的学习习惯。

四. 教学重难点1.有理数的乘方概念和性质的理解。

2.有理数乘方的运算法则的掌握。

3.乘方知识在实际问题中的应用。

五. 教学方法1.情境教学法：通过生活实例引入乘方概念，激发学生学习兴趣。

2.引导发现法：教师引导学生发现乘方的性质和运算法则，培养学生的自主学习能力。

3.实践操作法：让学生通过实际操作，加深对乘方知识的理解和掌握。

4.巩固拓展法：通过课堂练习和课后作业，巩固所学知识，提高学生的应用能力。

六. 教学准备1.教学PPT：制作包含乘方概念、性质和运算法则的PPT，以便于课堂展示和讲解。

2.教学案例：准备一些与生活紧密相关的乘方实例，以便于引导学生学习和应用。

3.练习题：准备一些有针对性的练习题，以便于课堂练习和课后巩固。

七. 教学过程1.导入（5分钟）利用生活实例引入乘方概念，如“2的3次方表示3个2相乘，即2×2×2=8”。

通过实例让学生感受乘方的意义，激发学生的学习兴趣。

2.呈现（10分钟）呈现乘方的性质和运算法则，如“乘方的性质：a m×a n=a(m+n)；乘方的运算法则：a m÷a n=a(m-n)”。

一次二次8个2个4个《有理数的乘方》（一）教案一、教学目标。

1、知识与技能目标：理解并掌握乘方、幂、底数、指数的概念及意义；能够正确进行有理数的乘方运算。

2、过程与方法目标：在生动的情境中让学生获得有理数乘方运算的初步经验；给学生充分观察、分析、概括的机会,让学生以动脑、动手、动口的方式培养自己探索归纳的能力，并从中感受“类比”的研究方法和“化归”的数学思想。

3、情感与态度目标：学生通过观察、分析、概括，总结出有理数乘方运算中符号的确定方法，从而感受探索的乐趣，增强数学学习的信心。

二、教学重难点。

教学重点：正确理解乘方的意义，掌握乘方的运算；教学难点：熟练掌握负底数幂的乘方运算。

三、教学方法。

在教学活动中，以学生为主体，通过创设合理的问题情境，给学生提供讨论交流的平台，我采用启发诱导式与自主探究式相结合的教学方法。

四、教学过程。

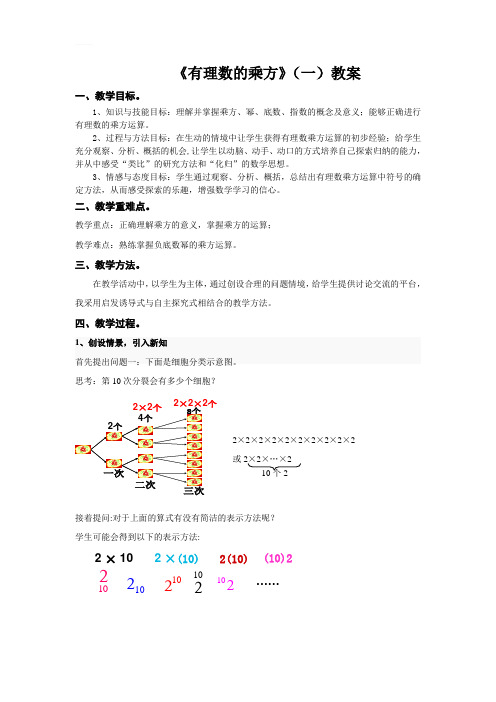
1、创设情景，引入新知首先提出问题一：下面是细胞分类示意图。

思考：第10次分裂会有多少个细胞？2×2×2×2×2×2×2×2×2×2或2×2×…×2 接着提问:对于上面的算式有没有简洁的表示方法呢？学生可能会得到以下的表示方法:2 ×102 ×(10)2(10)(10)2102102102102102……10个2n a 底数乘方的结果叫做幂然后提出问题二:边长为2的正方形面积以及边长为2的正方体体积分别是多少?22222×2=2222×2×2=3S=?V=?然后引导学生进行类比不难得到： 2×2×…×2 =102 紧接着再提出问题:2×2×…×2 = ?a ×a ×a …×a =? 学生不难得到结果如下：2×2×…×2 = 2na ×a ×a …×a =n a由此成功地引出乘方的定义，进入环节二的学习。

§3.3《有理数的乘方》教案山东省寿光市圣城街道第一初级中学孙冠美【教案背景】乘方运算对初二学生来说是一种新的运算，无论对本章的学习还是以后学习式的运算等都十分重要。

在此之前，学生已经学习了有理数的加、减、乘、除四则运算，具有相当的基础，在此基础上，通过有理数乘方运算，学生能体会转化思想，感知数学知识有普遍联系性、相互转化性。

同时，让学生经历和体验用所学的知识解决实际生活中问题的乐趣，感受到有理数运算的实用性和科学的探索方法，增强学好数学的信心。

【教学课题】有理数的乘方【教学目标】1、在现实背景中理解有理数乘方的意义。

2、总结、归纳出幂的符号规律3、合理的进行有理数的乘方运算【教学重点】有理数乘方的意义及幂的符号规律【教学难点】理解幂、指数、底数的概念【教学方法】师生互动、主动探索、合作交流【教具准备】多媒体课件【课前延伸】出示课件1、边长7厘米的正方形面积是多少？棱长5厘米的正方体体积是多少？2、一个正方形的边长为a，它的面积是，一个正方体的棱长是a，它的体积是。

【课内探究】（一）、请同学们拿出手中的纸，我们做个折叠游戏。

（二）、自主学习1、阅读课本61——62页上面三行，回答下列问题2、求几个的运算，叫做乘方，乘方的结果叫做，在a n中，a叫做幂的，n叫做幂的，a n读作 a n看作a的n次方的结果，也可读作【温馨提示】（1）一个数可以看作这个数本身的一次方，例如5就是51，a 就是a1指数是1通常省略不写。

（2）当底数是负数或分数时，要先用括号将底数括上，再在其右上角写上指数，指数要写得小些。

（三）、自我训练：1、13×13×13×13写成乘方的形式是（-2）×（-2）×（-2）写成乘方的形式是。

2、（-2）5中底数是，指数是，表示个-2相乘。

3、在-24中，底数是指数是结果是4、计算：53（-4）3 （-12）4 （-1）2011 -62从上面计算结果中你发现正数的乘方结果是什么数？负数的什么次幂是正数？负数的什么次幂是负数？你能得出一般结论吗？5、火眼金睛：不计算，判断下列运算结果的符号：（-3）13（-2）24 （-1.7）2011 （43）5（四）牛刀小试1、把-34x34x34写成乘方的形式是。

●课题有理数的乘方（一）●教学目标（一）教学知识点1．有理数乘方的意义．2．能进行有理数的乘方运算．（二）能力训练要求1．在现实背景中，理解有理数乘方的意义．2．能进行有理数的乘方运算．（三）情感与价值观要求通过师生共同交流，渗透利用数学知识解决实际问题的思想，以激发学生学习的兴趣，树立解决问题的信心．●教学重点有理数乘方的意义．●教学难点1．理解有理数乘方的意义上有困难．2．合理进行乘方运算．●教学方法讲练结合法●教具准备细胞分裂示意图投影片四张第一张：练习（记作§2．10．1 A）第二张：例1（记作§2．10．1 B）第三张：例2（记作§2．10．1 C）第四张：法则（记作§2．10．1 D）●教学过程Ⅰ．创设情景问题，引入课题［师］我们知道，每个生物体都是由细胞组成．动物由动物细胞组成，植物由植物细胞组成．活的细胞和生物体一样，也经过生长、衰老、死亡几个阶段．细胞本身的繁殖是以细胞分裂方式进行的．大家来观察一幅某种细胞分裂示意图：（出示“细胞分裂示意图”）这种细胞每过30分钟便由1个分裂成2个．想一想：经过5小时，这种细胞由1个能分裂成多少个？［生］1个细胞30分钟后分裂成2个，1个时分裂成4个，1．5小时后分裂成8个，2小时后分裂成16个，……，5小时后，这种细胞由1个能分裂成1024个．［师］对，1个细胞30分钟后分裂成2个，这是第一次分裂；1小时后分裂成4个，可以写成2×2，这是第二次分裂，1．5小时后分裂成8个，可写成2×2×2，这是第三次分裂，2小时后分裂成16个，也可写成2×2×2×2，这是第四次分裂，依次类推，想一想：5小时要分裂多少次？［生甲］5小时要分裂10次．［生乙］老师，我知道了，经过一次细胞分裂，1个可分裂成2个，经过二次分裂，1个可分裂成2×2个，经过三次分裂，1个可分裂成2×2×2个，这样依次类推，经过十次这样的分裂，1个便可分裂成［师］乙同学分析得很好，经过十次分裂后，1个细胞可以分裂成：个，但10个2相乘写起来挺麻烦的，为了简便，可将记为210，210表示有10个2相乘，我们把这种运算叫乘方．今天我们就来探讨有理数的乘方．Ⅱ．讲授新课［师］在小学中，我们把a×a记作a2，读作a的平方，或a的二次方．想一想：a×a 表示什么？［生］表示边长为a的正方形面积．［师］对，还把a×a×a记作a3，读作a的立方，或a的三次方．那a×a×a表示什么？［生］表示棱长为a的正方体的体积．［师］很好，刚才我们又把记作210．一般地，我们有：n个相同的因数a相乘，记作a n，即：这种求n个相同因数a的积的运算叫做乘方（Power）．乘方的结果叫做幂（Power）．在a n中，a叫做底数（base number）．n叫做指数（exponent）．a n读作a的n次方．a n看作是a的n 次方的结果时，也可读作a 的n 次幂．在这儿需要注意：乘方是一种运算，幂是乘方运算的结果．如：在94中，底数是9，指数是4，94读作9的4次方，或9的4次幂． 下面我们做一练习来熟悉这些概念（出示投影片§2．10 A ），口答： 1．填空： （1）（－1）12的底数是_____，指数是_____． （2）（－3）11表示_____个_____相乘． （3）（－21）5的指数是_____，底数是_____． （4）7．54的指数是_____，底数是_____． ［生］（－1）12的底数是－1，指数是12． （－3）11表示11个－3相乘． （－21）5的指数是5，底数是－21， 7．54的指数是4，底数是7．5．［师］很好．那5的底数是什么？指数是什么？ ［生］5的底数是5，没有指数． ［师］对吗？ ……［师］在这里需要注意：一个数可以看成这个数本身的一次方．如：5就是51，指数1通常省略不写．大家也可以这样理解：指数就是指相乘的因数的个数，指数是1，就是指只有一个因数．a n 就是n 个a 相乘，所以可以利用有理数的乘法运算来进行有理数的乘方运算． 下面通过例题来熟悉有理数的乘方运算．（出示投影片§2．10 B ）［例1］计算：（1）53； （2）（－3）4； （3）（－21）3解：（1）53=5×5×5=125． （2）（－3）4=（－3）·（－3）·（－3）·（－3）=81． （3）（－21）3=（－21）·（－21）·（－21）=－81注意：（1）当底数是负数或分数时，书写时一定要先用小括号将底数括上，再在其右上角写指数．如：（－3）4不能写成－34，（－21）3不能写成－213． （2）在不会引起误解的情况下，乘号也可以用“·”表示．例如：（－3）×（－3）×（－3）×（－3）×（－3） 可写成：（－3）·（－3）·（－3）·（－3）·（－3）接下来，我们做一练习来熟悉有理数的乘方运算（出示投影片§2．10 C ）1．计算： （1）（－1）10； （2）（－1）7； （3）83； （4）（－5）3； （5）（－0．1）3；（6）［生］解：（－1）10=1； （－1）7=－1；83=512；（－5）3=－125； （－0．1）3=－0．001；（－21）4=161； 102=100；103=1000；104=10000；（－10）2=100；（－10）3=－1000； （－10）4=10000［师］很好，大家都注意了底数是负数的乘方的表示．下面我们来观察刚才练习题的结果，你能发现什么规律？可互相交流．［生］正数的任何次幂都是正数；负数的偶次幂是正数，负数的奇次幂是负数． ［师］对．大家从计算结果中，归纳出乘方运算的符号法则：（出示投影片§2．10 D ）很好．大家再想一想：0的任何次幂等于多少？1的任何次幂等于多少？以10为底数的幂有何特点？［生］由有理数的乘法可以得到：0的任何非零次幂等于0，1的任何次幂等于1． 10的几次幂，在1的后面有几个0．［师］这位同学总结得非常正确．下面，我们通过课堂练习进一步熟悉有理数乘方的概念及其运算．Ⅲ．课堂练习 课本P 73 随堂练习 1．（1）在74中，底数是_____，指数是_____．（2）在（－31）5中，底数是_____，指数是_____． 答案：（1）7，4；（2）－31，52．计算：（1）（－3）3；（2）（－1．5）2；（3）（－71）2解：（1）（－3）3=（－3）·（－3）·（－3）=－27 （2）（－1．5）2=（－1．5）·（－1．5）=2．25 （3）（－71）2=（－71）·（－71）=4913．一个数的平方为16，这个数可能是几？一个数的平方可能是零吗？答案：一个数的平方为16，这个数是4或－4．一个数的平方可能是零．0的平方是0． 4．看课本P 72～73 5．试一试设n 为正整数，计算： （1）（－1）2n ． （2）（－1）2n +1．分析：n 为正整数时，2n 表示偶数，2n +1表示是奇数．所以由乘方的符号法则，即可得出．解：（－1）2n =1 （－1）2n +1=－1 Ⅳ．课时小结本节课主要学习了有理数的乘方的意义．有关概念及其有理数乘方运算．通过本节的学习，要明确乘方和加、减、乘、除一样，是一种运算，是求n 个相同因数的乘积的运算．乘方实质是一种特殊的乘法运算．幂与和、差、积、商一样，是乘方运算的结果．乘方运算与加减乘除的运算步骤一样，先确定符号，再计算绝对值．Ⅴ．课后作业（一）课本P 74习题2．13 １、2、3．3．1米长的小棒，第一次截去一半，第二次截去剩下的一半，如此截下去，第七次后剩下的小棒有多长？解：第七次后剩下的小棒有：（21）7=21×21×21×21×21×21×21=1281（米） （二）预习内容：课本P 75．准备一张白纸．Ⅵ．活动与探究1．如果｜a +1｜+（b －2）2=0，求（a +b ）39+a 34的值．过程：让学生通过讨论、探索知道：任何一个数的绝对值是一个非负数；任何一个数的平方也是一个非负数；两个非负数的和等于0，则这两个数都为0．这样：a 、b 即可解出．结果：因为｜a +1｜+（b －2）2=0 所以a +1=0，b －2=0 即a =－1，b =2因此（a +b ）39+a 34=［（－1）+2］39+（－1）34=1+1=2． 2．用计算器补充完整下表：31 32 33 34 35 36 37 38 392781从表中你发现3的方幂的个位数有何规律？3225的个位数是什么数字？为什么？过程：让学生用计算器填完表后，认真观察，找出规律，根据规律，确定3225的个位数字．结果：31 32 33 34 35 36 37 38 39278124372921876561从表中发现3的方幂的个位数呈周期性变化，变化周期是4． 因为225=56×4+1，所以3225的个位数是3．●板书设计§2．10．1 有理数的乘方（一）一、乘方：二、例1例2●备课资料 参考练习题 1．选择题：（1）109表示（ ）A ．10个9连乘B ．10乘以9C ．9个10连乘D ．9个10连加（2）一个数的平方是正数，那么这个有理数的立方是（ ） A ．正数 B ．负数 C ．正数或负数 D ．奇数 （3）一个数的平方等于它的倒数，这个数一定是（ ）A ．0B ．1C ．－1D ．2（4）计算（－1）2000+（－1）2001÷｜－1｜的值等于（ ）A ．0B ．1C ．－1D ．1或－1（5）关于（－3）4的正确说法是（ ） A ．－3是底数，4是幂B ．－3是底数，4是指数，－81是幂C ．3是底数，4是指数，81是幂D ．－3是底数，4是指数，81是幂 答案：（1）C （2）C （3）B （4）A （5）D2．把下列各式写成乘方运算的形式，并指出底数、指数各是什么？ （1）（－1．3）·（－1．3）·（－1．3）·（－1．3） （2）51×51×51×51×51×51 答案：（1）（－1．3）（－1．3）（－1．3）（－1．3）=（－1．3）4，其中，底数是－1．3．指数是4．（2）51×51×51×51×51×51=6)51(，其中：底数是51，指数是6． 3．计算：（1）（－5）2； （2）（－43）3；（3）（－101）4； （4）5×（－51)）3．答案：（1）25 （2）－6427) （3）100001) （4）－251。

青岛版数学七年级上册3.3《有理数的乘方》教学设计1一. 教材分析《青岛版数学七年级上册3.3《有理数的乘方》》这一节主要讲述有理数的乘方概念和性质。

学生在学习了有理数的乘除法和幂的定义基础上，进一步掌握有理数的乘方，有助于加深对数的概念的理解，为后续的代数运算和函数学习打下基础。

二. 学情分析七年级的学生已经掌握了有理数的加减乘除和幂的基本概念，具备了一定的逻辑思维能力。

但乘方作为幂的进一步延伸，其概念和性质较为抽象，学生可能难以理解。

因此，在教学过程中，需要结合实例，让学生通过观察、操作、思考，自主探索乘方的规律。

三. 教学目标1.理解有理数的乘方概念，掌握有理数乘方的运算方法。

2.理解有理数乘方的性质，能运用乘方解决实际问题。

3.培养学生的逻辑思维能力和自主学习能力。

四. 教学重难点1.有理数的乘方概念和性质。

2.有理数乘方的运算方法。

五. 教学方法采用“问题驱动”的教学方法，通过实例引入，引导学生观察、操作、思考，发现乘方的规律。

利用多媒体辅助教学，形象直观地展示乘方的过程，提高学生的学习兴趣。

同时，注重师生互动，鼓励学生提问、交流，提高学生的参与度。

六. 教学准备1.多媒体教学设备。

2.PPT课件。

3.练习题。

七. 教学过程1.导入（5分钟）利用多媒体展示一个实际问题：某商品打八折优惠，即原价的80%，求原价。

引导学生思考如何用数学方法表示这个问题，引出有理数的乘方概念。

2.呈现（10分钟）讲解有理数的乘方定义，引导学生通过观察、操作，发现有理数乘方的规律。

如：23表示2乘以自己3次，即2×2×2=8。

同时，讲解有理数乘方的运算方法，如：a m×a n=a(m+n)。

3.操练（10分钟）让学生进行一些有理数乘方的练习，巩固所学知识。

教师巡回指导，解答学生的疑问。

4.巩固（10分钟）讲解有理数乘方的性质，如：a m÷a n=a(m-n)；(a m)n=a(mn)。