混合多重图的边着色
- 格式:pdf
- 大小:93.80 KB
- 文档页数:3

离散数学着色基础知识离散数学是数学的一个重要分支,它关注离散的数学结构和对象。
在离散数学中,图论作为一个重要的研究领域,着色问题受到广泛的关注。
着色问题是指给定一个图的顶点或边,用不同的颜色给它们进行标记的问题。
本文将介绍离散数学中的着色基础知识,包括图的着色、四色定理以及一些常见的着色应用。
1. 图的着色在图的着色问题中,我们通常要求相邻的顶点或边不能使用相同的颜色。
对于给定的图,我们可以用一个函数来为每个顶点或边赋予一个颜色。
这个函数被称为着色函数。
如果对于每个相邻的顶点或边,它们被赋予了不同的颜色,那么这个着色函数就满足着色条件。
图的着色问题可以分为顶点着色和边着色两种情况。
在顶点着色中,我们使用不同的颜色为图中的每个顶点上色;而在边着色中,我们使用不同的颜色为图中的每条边上色。
通常情况下,我们更关注的是顶点着色问题。
2. 四色定理四色定理是图论中的一个著名的定理,它指出任意一个平面图都可以用四种颜色给其顶点进行着色,使得任意相邻的顶点使用不同的颜色。
具体地说,对于任意一个平面图,我们可以用四种颜色对其顶点进行着色,并且一定能够满足着色条件。
这个定理的证明非常复杂,涉及到大量的数学推理和计算。
它的证明分为两个步骤:首先,通过对所有可能的情况进行穷举和排除,证明了五种颜色是充分的;然后,通过反证法证明了四种颜色就足够了。
四色定理在实际应用中具有重要的意义。
它可以用来解决地图着色问题,即给定一幅地图,用尽可能少的颜色对每个行政区域进行着色,使得相邻的行政区域颜色不同。
四色定理的证明为解决这个问题提供了理论支持。
3. 着色的应用着色问题在现实生活中有许多应用。
除了地图着色问题外,还有课程表着色问题、时间表着色问题等等。
在课程表着色问题中,我们需要为学校的每个班级安排一个课程表,并且要求相邻时间段的课程使用不同的颜色。
这个问题可以转化为图的着色问题,其中图的每个顶点代表一个时间段,边代表时间段的相邻关系。
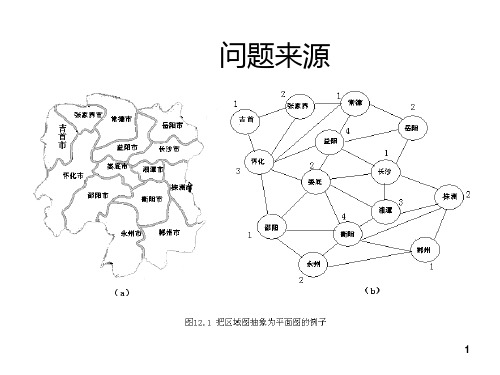

两类图的连续边着色的开题报告引言:图着色是图论中经典的问题之一,其中边着色问题是指给定一个无向图,对图中所有的边进行涂色,使得相邻的边颜色不同,并使用最少的颜色。
在图的连续边着色问题中,相邻的边按照一定顺序排列,需要求出至少需要涂多少种颜色才能满足相邻边颜色不同的条件。
本篇开题报告主要探讨两类图的连续边着色问题:树和圆方图。
首先介绍背景和意义,然后阐述问题描述和已有的相关研究,最后提出研究的主要目标和实现步骤。
背景:图着色问题是图论中的经典问题,是许多实际问题的抽象及其应用的基础,如地图着色、课表安排、调度问题等等。
边着色问题是应用领域中的经典问题之一,具有实际意义。
圆方图是一类特殊的图,在各种应用场景中都有着重要地位,如电路设计、图形表示、生物学等等。
研究意义:在实际应用中,能够有效地解决连续边着色问题可以提高工作效率和解决实际问题,如保证电路的正确设计和分析。
因此,研究连续边着色问题具有重要的理论和应用意义。
问题描述:树的连续边着色问题:给定一棵树,求其连续边着色数。
圆方图的连续边着色问题:给定一个圆方图,求其连续边着色数。
已有的相关研究:对于树的连续边着色问题,Gallian给出了一种线性时间求解方法,即一个树可由其一棵DFS树唯一确定,所以只需要对其DFS树进行边着色即可。
而对于圆方图的连续边着色问题,目前尚无明确的解决方法。
主要研究目标和实现步骤:树的连续边着色问题已有较为严谨的研究成果,因此本文的主要研究目标是解决圆方图连续边着色问题,具体的实现步骤如下:1. 对圆方图建模:选择合适的模型表示圆方图,便于对其进行求解。
2. 研究圆方图的特性:分析圆方图的特殊性质,探究其连续边着色问题的解决方法。
3. 设计算法并实现:在已有的研究基础上,设计一种有效的算法并进行实现,运用数学计算和计算机编程处理问题。
4. 对算法进行评价和应用:在实验数据下评价算法的效果,并将算法应用于实际问题,验证算法的实用性和有效性。


Nash-Williams定理是图论领域中的一个重要定理,它是由英国数学家C.St.J.A. Nash-Williams于1961年提出并证明的。
该定理在图的色彩问题中具有广泛的应用,对于解决复杂的图论问题具有重要意义。
下面我们将对Nash-Williams定理进行详细介绍。
Nash-Williams定理的内容主要包括以下几个方面:1. 定理内容Nash-Williams定理主要是关于图的边的着色的,它给出了一种特殊类型的边着色方法。
具体来说,对于任意给定的整数k,可以将一个图的所有边进行着色,使得从任意一个顶点出发,经过的所有边的颜色不超过k种。
2. 简单证明Nash-Williams定理的证明并不复杂,它可以通过归纳法来进行简单的推导。
首先可以证明当k=1时定理成立,然后可以假设当k=m时定理也成立,进而证明当k=m+1时定理同样成立。
在具体的证明过程中,需要利用一些图论中常用的技巧和方法,在适当的地方进行巧妙的转化和变换,最终得出结论。
3. 应用领域Nash-Williams定理在图的着色问题中具有广泛的应用。
在一些网络通信中,可以利用Nash-Williams定理进行信号的传输和编码,以保证通信信号的可靠性和稳定性。
在计算机科学中,Nash-Williams定理也可以应用于解决一些复杂的算法和优化问题。
4. 拓展与推广除了基本的Nash-Williams定理之外,在实际的应用和研究过程中可以对其进行一些拓展和推广。
例如可以考虑图的其他属性和特性,进一步探讨Nash-Williams定理在更一般情况下的成立条件和方法。
还可以将Nash-Williams定理与其他图论定理和算法相结合,形成更加完善和深入的理论体系。
Nash-Williams定理是图论中一个重要且有深远影响的定理,它在解决图的着色问题和相关领域具有重要的作用。
通过对Nash-Williams 定理的深入研究和应用,可以为图论领域的发展和实际问题的解决提供重要的理论支持和方法指导。

图论中的图的着色与染色问题图论是数学的一个分支,研究的是图的性质和图的应用。
在图论中,图的着色与染色问题是一个经典且重要的研究课题。
图的着色问题是指如何用有限的颜色对图的顶点或边进行染色,使得相邻的顶点或边具有不同的颜色。
本文将介绍图的着色与染色问题的基本概念和应用。
一、图的基本概念1. 无向图和有向图无向图由一些顶点和连接这些顶点的边组成,边没有方向性。
而有向图中,边是有方向性的,连接两个顶点的边有始点和终点之分。
2. 邻接矩阵和邻接表邻接矩阵是一种表示图的方法,用一个矩阵表示图中各个顶点之间的连接关系。
邻接表是另一种表示图的方法,用链表的形式表示图中各个顶点之间的连接关系。
二、图的着色问题图的着色问题是指如何用有限的颜色对图的顶点或边进行染色,使得相邻的顶点或边具有不同的颜色。
图的着色问题有以下两种情况:1. 顶点着色对于无向图或有向图的顶点,通过对每个顶点进行染色,使得图中任何相邻的顶点具有不同的颜色。
这里的相邻顶点指的是通过一条边相连的顶点。
2. 边着色对于无向图或有向图的边,通过对每条边进行染色,使得图中任何相邻的边具有不同的颜色。
这里的相邻边指的是有共同始点或终点的边。
三、图的染色算法对于图的着色问题,有不同的染色算法可以解决。
在这里我们介绍两种常用的染色算法:贪心算法和回溯算法。
1. 贪心算法贪心算法是一种基于局部最优策略的算法。
对于图的顶点着色问题,贪心算法的策略是从一个未染色的顶点开始,将其染上一个可用的颜色,并将该颜色标记为已占用,然后继续处理下一个未染色的顶点。
如果当前顶点没有可用的颜色可染,则需要增加一个新的颜色。
2. 回溯算法回溯算法是一种穷举所有可能性的算法。
对于图的着色问题,回溯算法的策略是从一个未染色的顶点开始,尝试不同的颜色进行染色,如果发现染色后与相邻顶点冲突,就回溯到上一个顶点重新尝试其他颜色,直到所有顶点都被染色。
四、图的着色问题的应用图的着色问题在实际中有广泛的应用。
四色定理证明方法全文共四篇示例,供读者参考第一篇示例:四色定理是数学上一个非常重要的定理,它指出任何一个地图都可以用四种颜色进行着色,使得相邻的区域彼此颜色不同。
这个定理虽然看似简单,但却是一个深奥的数学问题,其证明方法也非常复杂。
四色定理最早由英国数学家弗朗西斯·加思顿在1852年提出,并且在1976年由美国数学家凯尼思·阿普尔和沃夫冈·哈肯证明。
这个定理的证明方法主要是通过图论和逻辑推理来完成。
我们来介绍一下四色定理的一些基本概念。
在地图着色问题中,地图可以看作是由一些区域和它们之间的边界组成的。
而一个合法的地图着色方案就是给每个区域都分配一种颜色,使得相邻的区域颜色不同。
四色定理的证明方法涉及到很多复杂的数学理论,其中最主要的是图论。
图论是一门研究图和网络结构的数学学科,它在证明四色定理中起着至关重要的作用。
在证明四色定理时,数学家们首先将地图转化为一个特殊的图的形式,这个图被称为地图的双图。
地图的双图是在地图的基础上构造出来的一个图,在这个图中每个区域对应一个顶点,而边界对应一条连接这两个顶点的边。
这样一来,地图的问题就被转化为图的问题。
为了证明四色定理,数学家们需要证明对于任意一个地图的双图,我们都可以使用四种颜色进行着色。
证明的关键在于通过逻辑推理来排除一些特殊情况,使得我们只需要考虑一些简单的情况。
数学家们通过对图的结构和特性进行分析和归纳,最终找到了一种方法来证明四色定理的真实性。
除了图论,证明四色定理还涉及到概率论、逻辑推理和计算机算法等领域的知识。
数学家们通过将不同学科的知识相结合,从不同角度来审视这个问题,最终找到了证明四色定理的方法。
四色定理的证明方法是一个集合多种数学技巧和理论的综合性问题,它不仅考验数学家们的数学功底和逻辑思维能力,同时也展示了数学的复杂性和魅力。
四色定理虽然已经被证明,但它依然是数学领域中一个重要而且有趣的问题,相信在未来会有更多数学家对这个问题进行深入的研究和探索。
1、正常模式(Normal模式)——这是图层混合模式的默认方式,较为常用。
不和其他图层发生任何混合。
使用时用当前图层像素的颜色覆盖下层颜色。
因为在PhotoShop中颜色是当作光线处理的(而不是物理颜料),在Normal模式下形成的合成或着色作品中不会用到颜色的相减属性。
例如,在Normal模式下,在100%不透明红色选择上面的50%不透明蓝色选择产生一种淡紫色,而不是混合物理颜料时所期望得上到的深紫色。
当增大蓝色选择的不透明度时,结果颜色变得更蓝而不太红,直到100%不透明度时蓝色变成了组合颜色的颜色。
用Paintbrush I具以50%的不透明度把蓝色涂在红色区域上结果相同;在红色区域上描划得越多,就有更多的蓝色前景色变成区域内最终的颜色。
于是,在Normal 模式下,永远也不可能得到一种比混合的两种颜色成分中最暗的那个更暗的混合色了。
正常模式是Photoshop默认的模式。
这种模式的特点是混合色图层(当前图层)的不透明度及填充都是100%的时候,我们看不到基色图层(背景图层)。
我们需要降低混合色图层的不透明度才能显示基色图层,这时候混合色就会与基色混合形成结果色。
结果色跟混合色的不透明度有很多关系,她们的换算关系:结果色=混合色* 混合色不透明度值+ 基色* (100% - 混合色不透明度值)。
2、溶解模式(Dissolve模式)——溶解模式产生的像素颜色来源于上下混合颜色的一个随机置换值,与像素的不透明度有关。
将目标层图像以散乱的点状形式叠加到底层图像上时,对图像的色彩不产生任何的影响。
通过调节不透明度,可增加或减少目标层散点的密度。
其结果通常是画面呈现颗粒状或线条边缘粗糙化。
s4s R8D#f X| K j,CDissolve模式当定义为层的混合模式时,将产生不可须知的结果。
因此,这个模式最好是同Photoshop中的着色应用程序工具一同使用。
U1ssQlve模式采用100%不透明的前景色(或采样的像素,当与Rubber Stamp工具一起使用时),同底层的原始颜色交替以创建一种类似扩散抖动的效果。