17,18平面图及图的着色

图解塑料着色用有机颜料品种和性能(二)陈信华上海金泰色母粒有限公司201800中图分类号:TQ619.6文献标识码:C文章编号:DOI10.3969/j.issn.1008-1348.2015.06.008 1.2有机颜料十七系列产品品种和性能1.2.1双偶氮颜料双偶氮颜料是指颜料分子中含有两个偶氮基的颜料，一般是以二芳胺的重氮盐（3，3二氯联苯胺）与偶合组份（乙酰乙酰苯胺及其衍生物或双吡唑啉酮及其衍生物）偶合，就是著名的联苯胺系列颜料。

其色谱在强绿光黄色（颜料黄81，颜料黄17），中黄色（颜料黄14，颜料黄13）与红光黄色（颜料黄83）及橙色（颜料橙13，颜料橙34），几乎遍及黄色到橙色全色谱，见图2。

图2联苯胺系双偶氮颜料色度图双偶氮联苯胺颜料以着色力高，色泽鲜艳，价格经济而大量用于塑料着色，但性能一般,见表4，位于有机颜料结构和性能图最左边。

表4联苯胺系双偶氮有机颜料品种和性能联苯胺黄橙颜料用于聚合物加工温度超过200℃时会发生热分解，分解的产物是双氯联苯胺，双氯联苯胺是属于对动物有致癌性、对人体可能有致癌性的芳香胺.需注意颜料对人体和环境影响。

1.2.2单偶氮金属色淀黄为了改进单偶氮黄类颜料的耐热性和耐迁移性，在分子上引入磺酸基，再转化成色淀类颜料，其性能要比非色淀颜料要高得多。

单偶氮金属色淀黄类产品从绿光黄（颜料黄168）,中黄（颜料黄62）到红光黄（颜料黄191，颜料黄191：1，颜料黄183）见图3。

单偶氮金属色淀黄颜料位于有机颜料结构和性能图左偏中，性能也要比联苯胺系列颜料好的多，有些品种耐热性达280-300℃，耐候性达到3级以上见表5，是双偶氮联苯胺系列颜料代用品。

但该类颜料缺点着色力较低，有严重水渗性，价格也要比双偶氮系列颜料高。

图3单偶氮金属色淀黄颜料色度图表5单偶氮金属色淀黄色颜料性能1.2.3β类萘酚色淀红β类萘酚色淀颜料就是著名金光红C，是个鲜明黄光红，较优良耐热性，较经济价格，大量应用在塑料上，但耐光性，耐迁移性就差强人意，见表6表6β类萘酚色淀红颜料性能1.2.42B色淀红以磺酸基芳胺（俗称2B酸）重氮盐与2羟基-3萘甲酸（俗称2,3酸）偶合组份反应后金属色淀化，可有多种红色谱颜料，就是在塑料中大量应用的著名的2B红,以及宝红4B红颜料。

17.1 平面图的基本概念一、平面图及平面嵌入定义17.1如果图G能以这样的方式画在曲面S上，即除顶点处外无边相交，则称G可嵌入曲面S.若G可嵌入平面，则称G是可平面图或平面图。

画出的无边相交的图称为G的平面嵌入。

无平面嵌入的图称为非平面图。

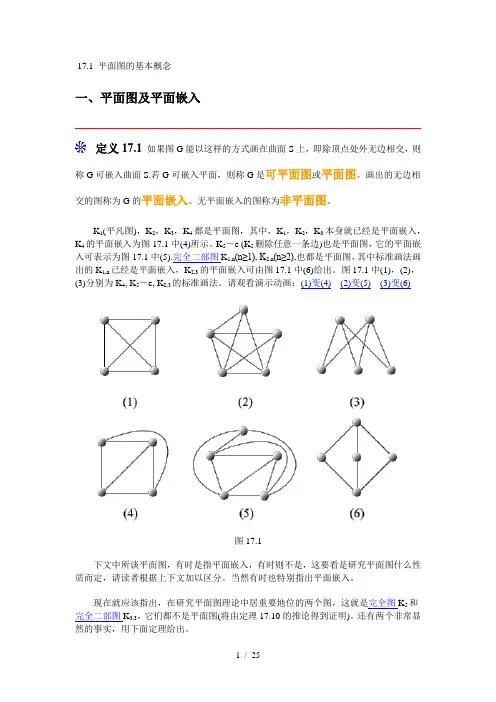
K1(平凡图)，K2，K3，K4都是平面图，其中，K1，K2，K3本身就已经是平面嵌入，K4的平面嵌入为图17.1中(4)所示。

K5－e (K5删除任意一条边)也是平面图，它的平面嵌入可表示为图17.1中(5).完全二部图K1,n(n≥1), K2,n(n≥2),也都是平面图，其中标准画法画出的K1,n已经是平面嵌入，K2,3的平面嵌入可由图17.1中(6)给出。

图17.1中(1)，(2)，(3)分别为K4, K5－e, K2,3的标准画法。

请观看演示动画：(1)变(4)(2)变(5)(3)变(6)图17.1下文中所谈平面图，有时是指平面嵌入，有时则不是，这要看是研究平面图什么性质而定，请读者根据上下文加以区分。

当然有时也特别指出平面嵌入。

现在就应该指出，在研究平面图理论中居重要地位的两个图，这就是完全图K5和完全二部图K3,3，它们都不是平面图(将由定理17.10的推论得到证明)。

还有两个非常显然的事实，用下面定理给出。

定理17.1若图G是平面图，则G的任何子图都是平面图。

由定理17.1立刻可知，K n(n≤4)和K1,n(n≥1)的所有子图都是平面图。

定理17.2若图G是非平面图，则G的任何母图也都是非平面图。

推论K(n≥5)和K3,n(n≥3)都是非平面图。

n本推论由K5，K3,3不是平面图及定理17.2得证。

还有一个明显的事实也用定理给出。

定理17.3设G是平面图，则在G中加平行边或环后所得图还是平面图。

本定理说明平行边和环不影响图的平面性，因而在研究一个图是否为平面图时可不考虑平行边和环。

二、平面图的面与次数定义17.2设G是平面图(且已是平面嵌入)，由G的边将G所在的平面划分成若干个区域，每个区域都称为G的一个面。

离散数学着色基础知识离散数学是数学的一个重要分支，它关注离散的数学结构和对象。

在离散数学中，图论作为一个重要的研究领域，着色问题受到广泛的关注。

着色问题是指给定一个图的顶点或边，用不同的颜色给它们进行标记的问题。

本文将介绍离散数学中的着色基础知识，包括图的着色、四色定理以及一些常见的着色应用。

1. 图的着色在图的着色问题中，我们通常要求相邻的顶点或边不能使用相同的颜色。

对于给定的图，我们可以用一个函数来为每个顶点或边赋予一个颜色。

这个函数被称为着色函数。

如果对于每个相邻的顶点或边，它们被赋予了不同的颜色，那么这个着色函数就满足着色条件。

图的着色问题可以分为顶点着色和边着色两种情况。

在顶点着色中，我们使用不同的颜色为图中的每个顶点上色；而在边着色中，我们使用不同的颜色为图中的每条边上色。

通常情况下，我们更关注的是顶点着色问题。

2. 四色定理四色定理是图论中的一个著名的定理，它指出任意一个平面图都可以用四种颜色给其顶点进行着色，使得任意相邻的顶点使用不同的颜色。

具体地说，对于任意一个平面图，我们可以用四种颜色对其顶点进行着色，并且一定能够满足着色条件。

这个定理的证明非常复杂，涉及到大量的数学推理和计算。

它的证明分为两个步骤：首先，通过对所有可能的情况进行穷举和排除，证明了五种颜色是充分的；然后，通过反证法证明了四种颜色就足够了。

四色定理在实际应用中具有重要的意义。

它可以用来解决地图着色问题，即给定一幅地图，用尽可能少的颜色对每个行政区域进行着色，使得相邻的行政区域颜色不同。

四色定理的证明为解决这个问题提供了理论支持。

3. 着色的应用着色问题在现实生活中有许多应用。

除了地图着色问题外，还有课程表着色问题、时间表着色问题等等。

在课程表着色问题中，我们需要为学校的每个班级安排一个课程表，并且要求相邻时间段的课程使用不同的颜色。

这个问题可以转化为图的着色问题，其中图的每个顶点代表一个时间段，边代表时间段的相邻关系。

平面图染色问题的研究引言平面图染色问题是一个经典的组合优化问题，它在图论中具有重要地位。

平面图染色问题旨在寻找一种给定的平面图的一种可行染色方案，使得相邻的顶点都获得不同的颜色。

自从1973年Gerhard Reinelt提出平面图染色问题以来，该问题一直是图论研究的热点之一。

本文旨在深入探讨平面图染色问题的研究现状和进展，以期为相关研究提供参考和启示。

正文部分1、平面图染色问题的概念平面图染色问题是指对于给定的平面图G，寻找一种映射f: V(G) →C，其中V(G)表示图的顶点集合，C表示颜色集合，使得对于任意相邻的顶点u和v，都有f(u) ≠ f(v)。

换句话说，平面图染色问题要求将图的顶点染上颜色，使得相邻顶点的颜色不同。

2、平面图染色模型及其应用平面图染色模型在诸多领域都有广泛的应用，如电路设计、蛋白质结构预测、印刷电路板设计、网页排版等。

例如，在电路设计中，通过将电路元件染上不同的颜色，可以避免电路短路和断路，提高电路的可靠性和稳定性。

在蛋白质结构预测中，通过将不同的氨基酸单元染上不同的颜色，可以帮助科学家们理解蛋白质的三维结构。

3、平面图染色问题的研究深入探讨自Reinelt提出平面图染色问题以来，大量的研究者致力于该问题的研究。

根据染色的方法和要求的不同，平面图染色问题可以分为多种类型，如k-染色、列表染色、反色数等问题。

其中，k-染色是最为常见的一种染色问题，它要求将图的顶点染上k种颜色，使得相邻顶点的颜色不同。

列表染色则要求对于每个顶点，都给出一个可行的颜色列表，使得该顶点的所有相邻顶点都不在其颜色列表中。

反色数则研究的是给定一个图，如何找到最少颜色数的染色方案。

结论部分本文对平面图染色问题进行了深入研究，总结了前人在该领域取得的研究成果，并指出了该领域存在的不足之处以及未来可能的研究方向。

虽然平面图染色问题已经被广泛研究了几十年，但是仍然有许多问题需要进一步探讨。

例如，对于特定类型的图，如何设计高效的染色算法？如何理解不同染色问题的最优解？此外，将平面图染色问题的研究成果应用于实际问题中，也是未来值得的方向之一。

[设计心得]彩色总平面制作扫盲总平填色（一）——制作概述总平填色的制作需要使用的软件主要是AutoCAD和PhotoShop这两个软件。

AutoCAD主要的作用是：前期对图纸整理并通过虚拟打印来打印输出TIFF格式文件，后期整个制作流程中对图纸的观察。

PhotoShop 主要的作用是：对AutoCAD输出的TIFF格式文件进行色彩的填充、材质的赋予、光影的分布、环境的美化等一系列的操作。

其中图01是AutoCAD格式的规划图，图02是经过PhotoShop处理后的总平填色图。

总平填色的制作流程：一、图纸的整理。

通常图纸的整理是将图纸整理分为整体框架层和文字说明层两层，遇到较为复杂的图纸我们可以根据需要把图层划分的更加细致，如建筑层、停车位层、铺装层、水系层等。

（使用软件：AutoCAD）二、图纸的打印与输出。

我们常用的输出格式是TIFF不压缩格式，但AutoCAD中默认的打印输出设置中没有TIFF不压缩格式，需要我们另行添加。

（使用软件：AutoCAD）三、整体大环境的处理。

在这个环节中我们主要是将AutoCAD输出的整体框架层和文字说明层合并到一个画布里，要把规划内部和外部的绿地划分开，主干道和小区内部道路划分开，以及对水系的基本色彩填充。

（使用软件：PhotoShop）四、建筑的处理。

在这个环节中我们要将建筑的部分制作出来，包括主体建筑部分的制作、女儿墙的制作、光影关系的处理、坡屋顶的处理、玻璃顶的处理等。

在有的规划中需要对已有建筑和拟建进行区分，对住宅和公建、商业进行区分。

（使用软件：PhotoShop）五、水系的处理。

在这个环节中我们要将水系的光感、色感、质感处理到位，有些规划中小区中央景观组团中还有喷泉和瀑布的制作。

（使用软件：PhotoShop）六、铺装的添加。

在这个环节中我们要将规划中的硬质铺装根据AutoCAD中规划的变化来分别添加。

（使用软件：PhotoShop）七、绿化的处理。

数学中的图的着色问题与四色定理数学中的图论是一门研究图及其性质的学科，其中一个重要的问题就是图的着色问题。

图的着色问题是指如何用有限种颜色给图的顶点或边进行染色，使得相邻的顶点或边不具有相同的颜色。

这个问题在实际应用中有着广泛的应用，比如地图着色、时间表的安排等。

在图的着色问题中，最著名的就是四色定理。

四色定理是指任何平面图都可以用四种颜色进行着色，使得相邻的区域不具有相同的颜色。

这个定理在1852年被英国数学家弗朗西斯·格思·韦尔斯顿和威廉·哈姆顿·伯奇证明，被认为是图论中的一个里程碑。

证明四色定理的过程非常复杂，需要运用大量的数学知识和技巧。

其中一个重要的思想就是通过对图进行适当的分割，将大问题转化为小问题，然后逐步解决。

这种分割的方法被称为“规约法”，即将一个复杂的问题规约为一系列简单的子问题。

通过这种方法，韦尔斯顿和伯奇最终证明了四色定理的正确性。

四色定理的证明引起了广泛的关注和讨论。

人们对于这个问题的兴趣不仅在于它的应用价值，更在于它背后的数学原理和思维方式。

四色定理的证明过程中，涉及到了众多的数学概念和定理，如图的平面性、图的连通性、图的染色等。

这些概念和定理的研究不仅推动了图论的发展，也对其他领域的数学研究产生了重要影响。

除了四色定理，图的着色问题还有其他一些重要的结果。

比如，五色定理指出任何平面图都可以用五种颜色进行着色，六色定理指出任何平面图都可以用六种颜色进行着色。

这些定理的证明过程和四色定理类似，都需要运用复杂的数学技巧和方法。

图的着色问题不仅在理论上有着重要的意义，也在实际应用中发挥着重要的作用。

比如，在地图着色中，我们可以用不同的颜色表示不同的国家或地区，以便更好地区分它们。

在时间表的安排中，我们可以用不同的颜色表示不同的活动或任务，以便更好地组织和管理。

这些应用都离不开图的着色问题的研究和应用。

总之，图的着色问题是数学中一个重要且有趣的问题。

《集合论与图论》课程教学大纲课程编号：N1030010课程名称：集合论与图论课程英文名称：Set Theory and Graph Theory总学时：48 讲课学时：48实验学时：0 习题课学时：0上机学时：0学分：3开课单位：计算机科学与技术学院授课对象：计算机科学与技术、信息安全、生物信息技术专业先修课程：工科数学分析、线性代数课程要求：必修课课程分类：专业基础课一、课程教学目的本课程为后继的专业基础课及专业课提供必要的数学工具，为描述离散模型提供了数学语言。

该课程的设置主要是为了培养学生的抽象思维和逻辑推理能力，提高学生分析问题和解决问题的能力，提高学生的数学修养及计算机科学素质。

要想用计算机解决问题就要为它建立数学模型，即描述研究对象及对象与对象之间的联系，并通过事物之间的联系找出事物的运动规律。

集合论与图论为此提供了强有力的描述工具与推理理论。

二、教学内容及学时安排本课程的内容分为两部分，即集合论与图论。

集合论是整个数学的基础之一，图论虽然可以看作是一个独立的数学分支，但在本课中可视为集合论的一个应用，它研究在一个有限集合上定义了一个二元关系所组成的系统。

教学内容包括：1．集合及其运算（4学时）集合、子集、集合的相等、集族、幂集；集合并、交、差、对称差、余集、笛卡尔乘积运算，各运算的性质及相互联系；有穷集合的基数、基本计数法则、容斥原理及应用。

2．映射（7学时）映射的基本定义及特殊性质、抽屉原理、映射的一般性质、映射的合成、逆映射、置换、二（n）元运算、特征函数。

3．关系（9学时）二（n）元关系、几个特殊二元关系、二元关系的表示、关系的合成运算、传递闭包、等价关系与集合的划分、偏序关系。

4．无穷集合及其基数（4学时）可数集及其性质、不可数集的存在—对角线法，基数及其比较、连续统。

5．图的基本概念（8学时）图、路、圈、连通图、偶图、补图、欧拉图、哈密顿图、图的邻接矩阵、最短路径问题。

6．树和割集（4学时）树及其性质、生成树、割点和桥及其特征性质，最小生成树问题。

图论中的图的着色与染色问题在图论中，图的着色与染色问题是一类经典的问题。

图的着色是指给图的每个顶点赋予一个颜色，要求相邻的顶点不能有相同的颜色；而图的染色是指给图的边赋予一个颜色，要求相邻的边不能有相同的颜色。

一、图的顶点着色图的顶点着色问题是图论中的经典问题之一。

给定一个无向图，要求为每个顶点分配一个颜色，使得任意两个相邻的顶点颜色不同。

这个问题的本质是将相邻的顶点划分到不同的颜色集合中。

解决图的顶点着色问题有多种算法，其中较为简单和常用的是贪心算法。

贪心算法按照某种规则为图的顶点逐个着色，每次着色时选择当前可用颜色的最小编号。

贪心算法的时间复杂度为O(n^2)，其中n 为图的顶点数。

二、图的边染色图的边染色问题是另一个经典的图论问题。

给定一个无向图，要求给每条边分配一个颜色，使得任意两条相邻的边颜色不同。

这个问题的目标是将相邻的边划分到不同的颜色集合中。

解决图的边染色问题的算法有多种，其中常用的是基于回溯法和深度优先搜索的算法。

回溯法通过递归地尝试为每条边分配颜色，并根据约束条件进行回溯，直到找到可行的解或者穷尽所有可能。

深度优先搜索则通过遍历图的边，逐个给边染色，当发现某条边与相邻边颜色相同时，回溯到前一条边重新选择颜色。

三、特殊图的着色与染色问题除了一般的图的着色与染色问题，还存在一些特殊类型的图，对应着特殊的着色与染色问题。

1. 树的着色与染色：在树中，任意两个顶点之间都只有一条路径，因此树的着色与染色问题可以简化为树的边染色问题。

树的边染色问题可以使用贪心算法解决，每次为某条边选择一个未使用的颜色，直到所有边都被染色。

2. 平面图的着色与染色：平面图是指可以画在平面上，且任意两条边最多只有一个公共顶点的图。

平面图的着色与染色问题是在满足平面图约束条件下对图进行着色或染色。

对于平面图的着色与染色问题，使用四色定理可以得到解，即任何平面图最多只需要四种颜色来着色或染色。

四、应用领域图的着色与染色问题在实际应用中具有广泛的应用。

§5.6 平面图与图地着色 习题5.61． 假定一个连通平面图有8个顶点,每个顶点地度数都为3。

请问,这个图地平面嵌入将平面分成多少个面？解 根据条件有8=p ,122/83=⨯=q ,从而根据欧拉定理有62=+-=p q f 。

2．设G 是具有k 个连通分图地)(q p ，平面图地一个平面嵌入,其面数为f ,证明：1+=+-k f g p解 下面用数学归纳法证明如下：（1）1=k 时即为欧拉公式,所以成立。

（2）假设m k ≤时公式成立。

（3）当1+=m 时,将图G 看成两个图1G 与2G 地并,其中1G 为一个连通分图, 2G 为其余m 个连通分图地并,根据上面地假设,对图1G 与2G 有：11111+=+-f q p ,1222+=+-m f q p ,将上两式相加得： 1)1()1()()(212121++=-+++-+m f f q q p p注意到图1G 与2G 共用一个外部面,我们即得1+=+-k f g p 。

3.假定一个)(q p ，图是连通地平面二部图,且p ≥3,则q ≤42-p 。

证;由于二部图中每个回路地长度都是偶数。

当p ≥3时,即每个面地围数至少是4。

据定理,2q ≥4f=4(2-p+q) 从而q ≤42-p 。

4．图5.42地4个图是平面图吗？如果是,给出一个平面嵌入;如果不是,找出与5K 或K 3,3同胚地子图。

图5.42 习题4地图解 图（1）,（2）,（4）改画如下：从而知图（1）,（2）是可平面图,图（4）是5阶完全图5K ,从而是非可平面图。

图（3）也是一个非可平面图,可用库拉托斯基定理证明如下：5．一个简单图地交叉数是指在平面里画这个图且不允许任何三条边在同一点交叉时,各边交叉地最少次数。

求以下非平面图地交叉数：3,3K , 5K , 6K , 7K , 4,3K , 4,4K , 5,5K解：3,3K 地交叉次数是15K 地交叉次数是56K 地交叉次数是107K 地交叉次数是184,3K 地交叉次数是84,4K 地交叉次数是115,5K 地交叉次数是166．下面地算法可以用来为简单图点着色。

图论中的图的着色与染色问题图是图论中的基本概念之一，是由顶点和边构成的数学结构。

在图的理论中，图的着色与染色问题是一个非常重要且有趣的研究领域。

本文将介绍图的着色与染色问题的基本概念、定理和算法，希望能够为读者深入了解图论领域提供一些帮助。

一、基本概念在图的理论中，图的着色与染色问题是指将图的顶点或边用不同颜色标记的过程。

着色是指给图的顶点或边分配颜色，使得相邻的顶点或边颜色不相同；而染色是指给图的顶点或边分配颜色，使得相邻的顶点或边颜色可以相同。

定理1：图的顶点着色问题对于一个简单图，顶点着色问题是指如何用最少的颜色将图的所有顶点着色，使得相邻的顶点颜色不同。

根据四色定理，任何一个平面图都可以只用四种颜色进行顶点着色。

定理2：图的边着色问题对于一个简单图，边着色问题是指如何用最少的颜色将图的所有边着色，使得任意两条依附于同一顶点的边颜色不同。

根据维茨定理，任何简单无向图都可以用最大度数加一种颜色进行边着色。

二、算法与实践在解决图的着色与染色问题时，常用的算法包括贪心算法、回溯算法、图染色算法等。

其中，Welsh-Powell算法是用来解决无向图的顶点着色问题的一种有效算法，其基本思想是优先考虑度数最大的顶点进行着色。

而在解决边着色问题时，常用的算法包括Vizing定理、边染色算法等。

三、应用与拓展图的着色与染色问题在实际生活中有着广泛的应用，如地图着色、时间表着色、调度问题等。

同时，在拓展领域中，图的着色与染色问题也与其他数学领域有着密切的联系，如组合数学、离散数学等，在各个领域都有着深入的研究与应用。

总结：图的着色与染色问题是图论领域中的一个重要研究方向，具有丰富的理论内涵和实际应用。

通过本文对图的着色与染色问题的介绍，希望读者能够对该领域有一个初步的了解，进一步深入研究与探讨。

愿本文能够为读者在图论领域的学习与研究提供一些帮助与启发。