统计作业(假设检验)

(第二版) (原假设与备择假设旳拟定)
1. 属于决策中旳假设检验
2. 不论是拒绝H0还是不拒绝H0，都必需采用 相应旳行动措施
3. 例如，某种零件旳尺寸，要求其平均长度为 10cm，不小于或不不小于10cm均属于不合 格
我们想要证明(检验)不小于或不不小于这两种 可能性中旳任何一种是否成立
4. 建立旳原假设与备择假设应为
H0: = 5
H1: 5
= 0.05
df = 10 - 1 = 9 临界值(s):
拒绝 H0
拒绝 H0
.025
.025
-2.262 0 2.262 t
8 - 20
检验统计量:
t = x 0 = 5.3 5 = 3.16
s n 0.6 10
决策：
在 = 0.05旳水平上拒绝H0
结论：
阐明该机器旳性能不好
符？( = 0.05)
统计学
(第二版)
均值旳单尾 t 检验
(计算成果)
H0: 40000 H1: < 40000 = 0.05 df = 20 - 1 = 19 临界值(s):
拒绝域
.05
-1.7291 0
t
8 - 23
检验统计量:
t = x 0
sn
= 41000 40000 = 0.894 5000 20
8 - 12
双侧检验
统计学
(第二版)
H0: = 0.081
H1: 0.081
= 0.05
n = 200
临界值(s):
拒绝 H0
拒绝 H0
.025
.025
-1.96 0 1.96 Z
8 - 13
检验统计量:

第三章 假设检验P1313.2 一种元件，要求其使用寿命不得低于1000（小时）。

现在从一批这种元件中随机抽取25件，测得其寿命平均值为950（小时）。

已知该种元件寿命服从标准差100σ=（小时）的正态分布，试在显著水平0.05下确定这批元件是否合格。

解：本题需检验0H ：0μμ≥，1H ：0μμ<.元件寿命服从正态分布，0σ已知，∴当0H成立时，选取统计量X u μ-=，其拒绝域为{}V u u α=<.其中950X =，01000μ=，25n =，0100σ=.则 2.5u ==-.查表得0.05 1.645u =-，得0.05u u <，落在拒绝域中，拒绝0H ，即认为这批元件不合格。

3.3 某厂生产的某种钢索的断裂强度服从正态分布()2N μσ，，其中40σ=（kg / cm 2）。

现从一批这种钢索的容量为9的一个子样测得断裂强度平均值为X ，与以往正常生产时的μ相比，X 较μ大20（kg / cm 2）。

设总体方差不变，问在0.01α=下能否认为这批钢索质量有显著提高？解：本题需检验0H ：0μμ=，1H ：0μμ>.钢索的断裂强度服从正态分布，0σ已知，∴当0H成立时，选取统计量u =，其拒绝域为{}1V u u α-=>.其中040σ=，9n =，020X μ-=，0.01α=.则 1.5u ==.查表得10.990.01 2.33u u u u αα-==-=-=，得0.99u u <，未落在拒绝域中，接受0H ，即认为这批钢索质量没有显著提高。

3.5 测定某种溶液中的水分。

它的10个测定值给出0.452%X =，0.035%S =。

设总体为正态分布()2N μσ，，试在水平5%检验假设：（i ）0H ：0.5%μ>； 1H ：0.5%μ<. （ii ）0H ：0.04%σ≥； 1H ：0.04%σ<. 解：（i ）总体服从正态分布，0σ未知，当0H成立时，选取统计量t =(){}1V t t n α=<-.查表得()()0.050.9599 1.8331t t =-=-.而()4.114 1.83311t t n α==-<-=-.落在拒绝域中，拒绝0H .（ii ）总体服从正态分布，μ未知， 当0H 成立时，选取统计量222nSχσ=，其拒绝域为(){}221V n αχχ=<-.查表得()20.059 3.325χ=.而()()()2222100.035%7.65610.04%n αχχ⨯==>-.未落在拒绝域中，接受0H .3.6 使用A （电学法）与B （混合法）两种方法来研究冰的潜热，样品都是－0.72℃的冰块，下列数据是每克冰从－0.72℃变成0℃水的过程中的吸热量（卡 / 克）：方法A ：79.98，80.04，80.02，80.04，80.03，80.03，80.04，79.97，80.05，80.03，80.02，80.00，80.02方法B ：80.02，79.94，79.97，79.98，79.97，80.03，79.95，79.97假定用每种方法测得的数据都服从正态分布，且它们的方差相等。

单组样本数据的t检验样本均数与总体均数标准值比较两组样本数据比较的t检验1成对数据配对设计均数的比较成组数据不配对两个均数的比较单样本t检验onesamplettest即比较抽样的单个样本均数与已知总体均数为理论值标准值的差别
统计假设检验
一、假设检验的概念与分类
假设检验(hypothesis test) 亦称显著 性检验(significance test)，是利用 样本信息，根据一定的概率水准，推断 指标(统计量) 与总体指标(参数)、不 同样本指标间的差别有无意义的统计分 析方法。
(3)确定P 值，作出推断结论
t 7.925 t0.05/ 2,9 2.262, p 0.05
同理 t=7.925＞t0.001/2,9=4.781,P＜0.001 结论；按 =0.05水准，拒绝 H0 ，p＜0.001， 差别有统计学意义。两种方法对脂肪含量的测 定结果不同，哥特里－罗紫法测定结果高于脂 肪酸水解法。
2．选择检验方法、计算统计量
根据：①研究目的， ②资料的类型和分布， ③设计方案， ④统计方法的应用条件， ⑤样本含量大小等， 选择适宜的统计方法并计算出相应 的统计量。
3．确定Ｐ值、做出推论
假设检验中的Ｐ值是指在由无效假设所 规定的总体作随机抽样，获得等于及大 于(和/或等于及小于)现有统计量的概 率。 即各样本统计量的差异来自抽样误差的 概率，它是判断H０成立与否的依据。
差值 d (4)=23 0.260 0.082 0.174 0.316 0.350 0.461 0.296 0.218 0.203 0.364 2.724
配对数据检验的统计量t，公式
d 0 d0 t Sd Sd / n
(3-16)
n -1

统计学中的假设检验（Hypothesis Testing in Statistics）统计学中的假设检验是一种统计推断方法，用于验证对总体参数或某个结论提出的假设是否是合理的。

它可以用来评估样本数据是否可以支持或反驳特定的假设，从而对研究问题进行分析和决策。

在假设检验中，我们通常提出一个零假设（null hypothesis）和一个备择假设（alternative hypothesis）。

零假设是一种无效假设，即我们认为没有关联或没有差异存在。

备择假设是一种我们希望证明的假设，即存在某种关联或差异。

在进行假设检验时，我们首先收集样本数据。

然后，我们基于这些数据计算一个统计量，该统计量可以用于判断是否可以拒绝零假设。

统计学家们使用最常见的统计量是p值（P-value）。

p值是在给定零假设成立的条件下，观察到结果或更极端结果的概率。

如果p值小于预先设定的显著性水平α（通常为0.05），我们可以拒绝零假设，并接受备择假设。

举例来说，假设我们想要研究某药物对某种疾病的治疗效果。

零假设可以是该药物对治疗效果没有明显影响，备择假设可以是该药物对治疗效果有显著影响。

我们收集了一组患有该疾病的患者，并将其随机分为两组，对其中一组使用药物进行治疗，另一组使用安慰剂进行治疗。

然后，我们比较两组的治疗效果。

通过对比两组的数据，我们可以计算出一个p值。

如果p值小于我们设定的显著性水平α，我们可以拒绝零假设，即药物对治疗效果具有显著影响。

反之，如果p值大于α，我们无法拒绝零假设，即药物对治疗效果没有明显影响。

在假设检验中，还有两种错误可能性：第一类错误和第二类错误。

第一类错误是当真实情况下零假设正确时，我们错误地拒绝了它。

第二类错误是当真实情况下备择假设正确时，我们错误地接受了零假设。

通常，我们在设计假设检验时将第一类错误的概率控制在一个较小的水平上（如0.05），而第二类错误的概率则可能较大。

在实际应用中，假设检验是一种重要的工具，被广泛用于各种领域和学科，如医学研究、社会科学、工程等。

10
即 z 拒绝域，没有落入接受域，所以没有足够理由接受原假设H0, 同
时，说明该类型电子元件的使用寿命确实有了显著的提高。
第六章 假设检验
1. 正态总体均值的假设检验
(2) 总体方差 2 未知的情形
双侧举例：【例 6-6】某厂用生产线上自动包装的产品重量服从正态
分布，每包标准重量为1000克。现随机抽查9包，测得样本平均重量为
100个该类型的元件，测得平均寿命为102(小时), 给定显著水平α=0.05,
问，该类型的电子元件的使用寿命是否有明显的提高？
解：该检验的假设为右单侧检验 H0: u≤100, H1: u>100
已知 z z0.05 1.645
zˆ x u0 n 100 (102 100 ) 2 1.645
986克，样本标准差是24克。问在α=0.05的显著水平下,能否认为生产线
工作正常？ 解：该检验的假设为双侧检验 H0: u=0.5, H1: u≠0.5
已知 t /2 (n 1) t0.025 (9 1) 2.306， 而 tˆ x u 986 1000 1.75 可见 tˆ 1.75 2.306
设H0, 同时，说明该包装机生产正常。
其中 P( Z 1.8) 1 P( Z 1.8) 1 0.9281 0.0719 0.05。
第六章 假设检验
单侧举例：【例 6-4】某电子产品的平均寿命达到5000小时才算合格，
现从一批产品中随机抽出12件进行试验，产品的寿命分别为
5059, 3897, 3631, 5050, 7474, 5077, 4545, 6279, 3532, 2773, 7419, 5116
的显著性水平=0.05，试测算该日生产的螺丝钉的方差是否正常？

0.025
决策： ∵Z值落入接受域， ∴在α=0.05的显著水平上接受 H 0 。
结论：有证据表明现在生产的铁水平均含碳量与以前没有显著差 异，可以认为现在生产的铁水平均含碳量为4.55。
8.2 一种元件，要求其使用寿命不得低于700小时。现从一批这种 元件中随机抽取36件，测得其平均寿命为680小时。已知该元件寿 命服从正态分布，σ=60小时，试在显著性水平0.05下确定这批元 件是否合格。
甲法：31 34 29 32 35 38 34 30 29 32 31 26 乙法：26 24 28 29 30 29 32 26 31 29 32 28 两总体为正态总体，且方差相同。问两种方法的装配时 间有无显著差别(α =0.05)？ 解： 正态总体，小样本，σ²未知但相同，独立样本t检验 H 0 : 甲 -乙 = 0 H1 : 甲 - 乙 ≠ 0
由Excel制表得：
由图可知：
已知：α = 0.05，n1 = n2=12 2 2 x甲 =31.75 x乙 =28.67 S甲=10.20 S乙 =6.06 t=1.72 t∈(-1.72,1.72)接受，否则拒绝。 t=(31.75-28.67)/(8.08* 0.41)=0.93 0.93∈(-1.72,1.72) 决策：在α = 0.05的水平上接受H 0 。 结论: 两种方法的装配时间无显著不同。
σ²≤100 H 1 : σ²＞100 α= 0.05，n=9，自由度= 9 - 1 = 8， S² =215.75， x =63 采用χ²检验 临界值(s): χ² =15.5 ）S 2 (9 - 1) * 215.75 2 （n - 1 17.26 15.5 检验统计量： 2 100 决策：在 a = 0.05的水平上拒绝 H 0 结论: σ²＞100

一、单选题1、在假设检验中，我们认为（）。

A.原假设是不容置疑的B.拒绝域总是位于检验统计量分布的两边C.小概率事件在一次抽样中实际上不会发生D.检验统计量落入拒绝域是不可能的正确答案：C2、在假设检验中，显著性水平确定后（）。

A.双边检验的拒绝域小于单边检验的拒绝域B.双边检验的拒绝域大于单边检验的拒绝域C.双边检验的拒绝域与单边检验的拒绝域不可简单直接对比D.双边检验的拒绝域等于单边检验的拒绝域正确答案：C3、单个正态总体均值的检验时若总体方差已知，（）。

A.设计的检验统计量服从卡方分布B.设计的检验统计量服从F分布C.设计的检验统计量服从标准正态分布D.设计的检验统计量服从t分布正确答案：C4、总体成数的假设检验（）。

A.设计的检验统计量服从标准正态分布B.设计的检验统计量服从卡方分布C.设计的检验统计量近似服从卡方分布D.设计的检验统计量近似服从标准正态分布正确答案：D5、两个正态总体均值之差的检验中，如果两个总体方差未知但相等，检验统计量t的自由度是（）。

A.两样本容量之和B.两样本容量之和减2C.两样本容量之积D.两样本容量之和减1正确答案：B6、假设检验是检验（）的假设值是否成立。

A.总体均值B.总体指标C.样本方差D.样本指标正确答案：B7、在大样本条件下，样本成数的抽样分布近似为（）。

A.均匀分布B.卡方分布C.二项分布D.正态分布正确答案：D8、下列关于假设检验的说法，不正确的是（）。

A.作出“拒绝原假设”决策时可能会犯第一类错误B.作出“不能拒绝原假设”决策时意味着原假设正确C.作出“不能拒绝原假设”决策时可能会犯第二类错误D.作出“接受原假设”决策时意味着没有充分的理由认为原假设是错误的正确答案：B9、将由显著性水平所规定的拒绝域平分为两部分，置于概率分布的两，每边占显著性水平的二分之一，这是（）。

A.右侧检验B.单侧检验C.左侧检验D.双侧检验正确答案：D10、如果使用者偏重于担心出现纳伪错误而造成的损失，则应把显著性水平定得（）。

第三章 假设检验课后作业参考答案3.1 某电器元件平均电阻值一直保持2.64Ω，今测得采用新工艺生产36个元件的平均电阻值为2.61Ω。

假设在正常条件下，电阻值服从正态分布，而且新工艺不改变电阻值的标准偏差。

已知改变工艺前的标准差为0.06Ω，问新工艺对产品的电阻值是否有显著影响？(01.0=α)解：(1)提出假设64.2:64.2:10≠=μμH H ， (2)构造统计量36/06.064.261.2/u 00-=-=-=nX σμ(3)否定域⎭⎬⎫⎩⎨⎧>=⎭⎬⎫⎩⎨⎧>⋃⎭⎬⎫⎩⎨⎧<=--21212αααu u uu u u V (4)给定显著性水平01.0=α时，临界值575.2575.2212=-=-ααuu ，(5) 2αu u <，落入否定域，故拒绝原假设，认为新工艺对电阻值有显著性影响。

3.2 一种元件,要求其使用寿命不低于1000（小时）,现在从一批这种元件中随机抽取25件,测得其寿命平均值为950（小时）。

已知这种元件寿命服从标准差100σ=（小时）的正态分布，试在显著水平0.05下确定这批元件是否合格。

解：{}01001:1000, H :1000X 950 100 n=25 10002.5V=u 0.05H x u αμμσμα-≥<====->=提出假设：构造统计量：此问题情形属于u 检验，故用统计量：此题中：代入上式得：拒绝域：本题中：0.950.950u 1.64u 0.0u H =>∴即，拒绝原假设认为在置信水平5下这批元件不合格。

3.3某厂生产的某种钢索的断裂强度服从正态分布()2,σμN ，其中()2/40cm kg =σ。

现从一批这种钢索的容量为9的一个子样测得断裂强度平均值为X ，与以往正常生产时的μ相比，X 较μ大20(2/cm kg )。

设总体方差不变，问在01.0=α下能否认为这批钢索质量显著提高？ 解：(1)提出假设0100::μμμμ>=H H ， (2)构造统计量5.13/4020/u 00==-=nX σμ (3)否定域{}α->=1u u V(4)给定显著性水平01.0=α时，临界值33.21=-αu(5) α-<1u u ，在否定域之外，故接受原假设，认为这批钢索质量没有显著提高。

1．假设某产品的重量服从正态分布，现在从一批产品中随机抽取16件，测得平均重量为820克，标准差为60克，试以显著性水平α=0.01与α=0.05，分别检验这批产品的平均重量是否是800克。

解：假设检验为800:,800:0100≠=μμH H (产品重量应该使用双侧 检验)。

采用t 分布的检验统计量nx t /0σμ-=。

查出α＝0.05和0.01两个水平下的临界值(df=n-1=15)为2.131和2.947。

667.116/60800820=-=t 。

因为t <2.131<2.947，所以在两个水平下都接受原假设。

2．某牌号彩电规定无故障时间为10 000小时，厂家采取改进措施，现在从新批量彩电中抽取100台，测得平均无故障时间为10 150小时，标准差为500小时，能否据此判断该彩电无故障时间有显著增加(α=0.01)？解：假设检验为10000:,10000:0100>=μμH H （使用寿命有无显著增加，应该使用右侧检验）。

n=100可近似采用正态分布的检验统计量nx z /0σμ-=。

查出α＝0.01水平下的反查正态概率表得到临界值2.32到2.34之间（因为表中给出的是双侧检验的接受域临界值，因此本题的单侧检验显著性水平应先乘以2，再查到对应的临界值）。

计算统计量值3100/5001000010150=-=z 。

因为z=3>2.34(>2.32)，所以拒绝原假设，无故障时间有显著增加。

3.设某产品的指标服从正态分布，它的标准差σ已知为150，今抽了一个容量为26的样本，计算得平均值为1637。

问在5％的显著水平下，能否认为这批产品的指标的期望值μ为1600?解: 01:1600, :1600,H H μμ=≠标准差σ已知,拒绝域为2Z z α>,取0.05,α=26,n =0.0250.9752 1.96z z z α===,由检验统计量1.25 1.96Z ===<,接受0:1600H μ=, 即,以95%的把握认为这批产品的指标的期望值μ为1600.4.某电器零件的平均电阻一直保持在2.64Ω，改变加工工艺后，测得100个零件的平均电阻为2.62Ω，如改变工艺前后电阻的标准差保持在O.06Ω，问新工艺对此零件的电阻有无显著影响(α=0.05)?解: 01: 2.64, : 2.64,H H μμ=≠已知标准差σ=0.16,拒绝域为2Z z α>,取0.02520.05, 1.96z z αα===,100,n =由检验统计量3.33 1.96Z ===>,接受1: 2.64H μ≠, 即, 以95%的把握认为新工艺对此零件的电阻有显著影响.5．某食品厂用自动装罐机装罐头食品，每罐标准重量为500克，每隔一定时间需要检查机器工作情况。

第 8 章
假设检验
雪儿·海蒂(Shere Hite)在1987年出版的《女性与爱情:前进中的文化之旅》一书中给
出了大量数据:
● 84%的女性“在情感上对两性关系不满意”(804页)。
● 95%的女性“在恋爱时会因男友而产生情感及心理上的烦恼”(810页)。
● 84%的女性“在与男友的恋爱中有屈尊感”(809页)。
他对这个问题很感兴趣。他兴奋地说道：“让我
们来检验这个命题吧！”并开始策划一个实验。
在实验中，坚持茶有不同味道的那位女士被奉上
一连串的已经调制好的茶，其中，有的是先加茶
后加奶制成的，有的则是先加奶后加茶制成的。
Hypothesis Testing
接下来，在场的许多人都热心地加入到实验中来。
几分钟内，他们在那位女士看不见的地方调制出
Hypothesis Testing
同样，即便这位女士能做出区分，她仍然有猜错的
可能。或者是其中的一杯与奶没有充分地混合，或
者是泡制时茶水不够热。即便这位女士能做出区分
，也很有可能是奉上了10杯茶，她却只是猜对了
其中的9杯。
Hypothesis Testing
是奶加到茶里，还是茶加到奶里？
假设：她没有这种分辨能力，是碰巧猜对的！
假设其中真有99个白球，摸出
红球的概率只有1/100，这是
小概率事件。
小概率事件在一次试验中竟然发生了，不能不
使人怀疑所作的假设。
这个例子中所使用的推理方法，可以称为
带概率性质的反证法
它不同于一般的反证法
一般的反证法要求在原假设成立的条件
下导出的结论是绝对成立的，如果事实与之
矛盾，则完全绝对地否定原假设。
…99个

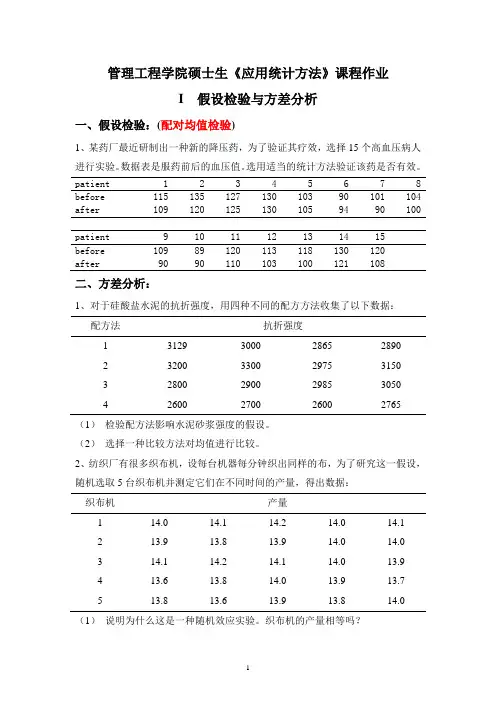
管理工程学院硕士生《应用统计方法》课程作业I 假设检验与方差分析一、假设检验：(配对均值检验)1、某药厂最近研制出一种新的降压药，为了验证其疗效，选择15个高血压病人进行实验。

数据表是服药前后的血压值。

选用适当的统计方法验证该药是否有效。

patient 1 2 3 4 5 6 7 8 before 115 135 127 130 103 90 101 104 after 109 120 125 130 105 94 90 100patient 9 10 11 12 13 14 15before 109 89 120 113 118 130 120after 90 90 110 103 100 121 108二、方差分析：1、对于硅酸盐水泥的抗折强度，用四种不同的配方方法收集了以下数据：配方法抗折强度1 3129 3000 2865 28902 3200 3300 2975 31503 2800 2900 2985 30504 2600 2700 2600 2765（1）检验配方法影响水泥砂浆强度的假设。

（2）选择一种比较方法对均值进行比较。

2、纺织厂有很多织布机，设每台机器每分钟织出同样的布，为了研究这一假设，随机选取5台织布机并测定它们在不同时间的产量，得出数据：织布机产量1 14.0 14.1 14.2 14.0 14.12 13.9 13.8 13.9 14.0 14.03 14.1 14.2 14.1 14.0 13.94 13.6 13.8 14.0 13.9 13.75 13.8 13.6 13.9 13.8 14.0（1）说明为什么这是一种随机效应实验。

织布机的产量相等吗？（2）估计织布机间的变异。

（3）估计实验的误差方差。

3、电视机厂感兴趣于对彩色显像管四种不同的涂层对显像管的电导率是否有影响。

测得电导率的数据如下：涂层电导率1 143 141 150 1462 152 149 137 1433 134 136 132 1274 129 127 132 129 （1）涂层使电导率有差异吗？（2）估计总均值与处理效应。

假设检验：1. （卢淑华课后练习）根据某公司的上报，平均每天的营业额为55万元。

经过6天的普查，其营业额为（设营业额满足正态分布）：592000元683000元578000元565000元637000元573000元。

问：原摊贩上报的数字是否可信？（显著性水平=0.05）解题：（1）原假设H0：u = 55万元即经普查所得的平均每天的营业额与55万元无显著差异。

备择假设H1 : u 不等于55万元即经普查所得的平均每天的营业额与55万元存在显著差异。

（2）选择的检验统计量为t统计量（3）（4）分析：单样本t检验的t统计量的观测值为2.904，对应的概率p-值（sig.）为0.031。

给定的显著性水平a=0.05, 由于概率p-值小于显著性水平a，因此应该拒绝原假设，认为经普查所得的平均每天的营业额与55万元存在显著差异。

同时55万元没有在相应的95%的置信区间，也证实了上述结论。

2、工作人员宣称水样中钙的均值为每立方米20.7克，现用某方法重复测定该水样11次，分别测得每立方米钙的含量为：20.99 20.41 20.10 20.00 20.91 22.60 20.99 20.41 23.00 22.00 20.00 。

问该方法测得的均值是否偏高？（0.05）解题：（1）（单样本t检验）原假设：用此方法测得的均值与20.7克无显著差异。

备择假设（2）选择的检验统计量为t 统计量分析：t统计量的观测值为1.064，对应的概率p-值为3.312。

给定的显著性水平为a=0.05，由概率p-值大于0.05，因此接受原假设，认为用此方法测得的均值与20.7克无显著差异。

同时20.7克在相应的95%的置信区间内也证实了这点。

3、长春市政府官员宣称，长春市居民的生活水平已经明显提高，平均居民月收入已经达到1200元。

现以抽样调查方法来验证该官员的说法是否正确，随机抽样15名居民，他们的月收入分别为：1350 1300 1100 1200 1250 1000 1100 1350 1200 1150 1050 1100 1150 1200 1250 ，根据这个调查结果，如何评价该官员的说法？解题：（单总体t检验）（1）原假设：居民平均收入与1200无显著差异（2）选择检验统计量为t统计量4. 对两种不同的水稻品种A和B分别统计了8个地区的单位面积产量（公斤），得到下面数据：A品种：86 87 56 93 84 93 75 79B品种：80 79 58 91 77 82 76 66要求检验两个水稻品种的单位面积产量之间是否有显著。

实验三假设检验
一、实验目的
通过本次实验，了解如何进行各种类型参数检验和非参数检验。

二、实验性质
必修，基础层次
三、主要仪器及试材
计算机及SPSS软件
四、实验内容
1.单一样本T检验
2.独立样本T检验
3.配对样本T检验
4.非参数卡方检验
五、实验学时
4学时
六、上机作业
（2）学生的体重是否等于45公斤？
2.双样本T 检验（Independent-Samples T Test 过程）
分别测得14例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇
某单位研究饲料中缺乏维生素E 与肝中维生素A 含量的关系，将大白鼠按性别、体重等配为8对，每对中两只大白鼠分别喂给正常饲料和维生素E 缺乏饲料，一段时期后将之宰杀，测定其肝中维生素A 含量（μmol/L ）如下，问饲料
4.如下表
5.某工厂生产一批产品,质量检查规定:其次品率05.00≤p ,则这批产品可以出厂,否则不能出厂. 现从这批产品中抽查50件产品,发现有4件次品,试问这批产品能否出厂?(提示:用非参数的二项分布检验05.00≤p 是否可接受)。

左侧检验：
×
抽样分布
Region of Rejection
拒绝H0
置信水平
1 -
Region of Non rejection
临界值
H0
观察到的样本统计量
【例3】一家研究机构估计，某城市中家庭拥有汽车的比例超 过30%。为验证这一估计是否正确，该研究机构随机抽取 了一个样本进行检验。试陈述用于检验的原假设与备择 假设。
36.6
36.9
36.7
37.2
36.3
37.1
36.7
36.8
37.0
37.0
36.1
37.0
根据样本数据，计算的平均值为36.8oC，标准差为0.36oC 根据参数估计方法，健康成年人平均体温的95%的置信区
间为(36.7，36.9) 研究人员发现这个区间内并没有包括37oC！ 因此，提出了“不应该再把37oC作为正常人体温的一个有
解：研究者抽检的意图是倾向于证实这种洗涤剂的平均
净含量并不符合说明书中的陈述。
建立的原假设和备择假设为：
H0 ： 500 H1 ： < 500
<提出假设>
【例3】一家研究机构估计，某城市中家庭拥有汽车的比例超 过30%。为验证这一估计是否正确，该研究机构随机抽取 了一个样本进行检验。试陈述用于检验的原假设与备择 假设。
传统上，做出决策所依据的是样本统 计量，现代检验中人们直接使用由统计量
算出的犯第一类错误的概率，即所谓的P
值。
注：假设检验不能证明原假设正确。
① 假设检验只提供不利于原假设的证据。当拒绝原假设时， 表明样本提供的证据证明它是错误的；当没有拒绝原假设时 ，我们也不说“接受原假设”，因为没法证明原假设是正确 的

假设检验作业1. 一种罐装饮料采用自动生产线生产，每罐的容量是255ml （总体的均值 ），标准差为5ml （总体的标准差）。

为检验每罐容量是否符合要求，质检人员在某天生产的饮料中随机抽取了40罐进行检验，测得每罐平均容量为255.8ml （样本的均值）。

取显著性水平=0.05 ，检验该天生产的饮料容量是否符合标准要求？ 解：正态，总体方差已经，大样本，Z 检验统计量，双侧检验 96.105.040/52558.255)1,0(~n /2552552010==-=-=≠=αασμμμZ N X Z H H ：： 若计算的Z 值在（-1.96，1.96）之间，不能拒绝原假设，认为符合标准；反之，拒绝原假设，即产品不符合标准。

2. 某一小麦品种的平均产量为5200kg/hm2 。

一家研究机构对小麦品种进行了改良以期提高产量。

为检验改良后的新品种产量是否有显著提高，随机抽取了36个地块进行试种，得到的样本平均产量为5275kg/hm2，标准差为120/hm2 。

试检验改良后的新品种产量是否有显著提高？ (a=0.05)解：不知是否正态总体，总体标准差未知，但因是大样本，可用Z 分布检验统计量，右侧检验（注意临界值或拒绝域的确定，用图形表示更清楚）645.105.036/12052005275)1,0(~n /52005200010==-=-=≤ααμμμZ N s X Z H H ：：计算出的Z 值，若Z 值大于1.645则拒绝原假设；反之，不能拒绝原假设。

3. 一种以休闲和娱乐为主题的杂志，声称其读者群中有80%为女性。

为验证这一说法是否属实，某研究部门抽取了由200人组成的一个随机样本，发现有146个女性经常阅读该杂志。

分别取显著性水平 a=0.05和a=0.01 ，检验该杂志读者群中女性的比率是否为80%？注意：（1)有些书，用大写的π表示总体比例。

（2) 不同的显著性水平，可能得出不同的结论。

统计学中的假设检验方法统计学是一门研究数据收集、分析和解释的科学领域。

在统计学中，假设检验方法是一种常用的数据分析技术，用于对研究假设进行验证。

通过对样本数据进行分析和推断，假设检验方法可以帮助研究人员判断某种假设在总体中是否成立，从而对问题进行科学的解答。

一、假设检验的基本概念假设检验是基于样本数据的统计推断方法，其基本思想是通过对样本数据进行统计分析，以便对总体参数进行推断和判断。

在假设检验中，我们通常会提出一个原假设（H0）和一个备择假设（H1或Ha），并通过计算统计量的方法来判断是否拒绝原假设。

原假设（H0）通常是一种无足够证据反驳的假设，研究人员试图通过数据分析来证明其成立。

备择假设（H1或Ha）则是原假设的对立假设，即研究人员试图证明原假设不成立。

二、假设检验的步骤在进行假设检验时，通常需要经过以下步骤：1. 建立假设：明确原假设（H0）和备择假设（H1或Ha），并确定显著性水平。

2. 选择合适的检验统计量和分布：根据数据类型和假设条件选择合适的检验统计量，并明确其分布情况（如正态分布、t分布、卡方分布等）。

3. 计算检验统计量的值：利用收集到的样本数据，计算出具体的检验统计量的值。

4. 计算P值：根据检验统计量的值和对应的分布情况，计算出P值（即在原假设成立的情况下，观察到的统计量或更极端情况出现的概率）。

5. 判断拒绝或接受原假设：比较P值与事先设定的显著性水平（通常为0.05或0.01），如果P值小于显著性水平，则拒绝原假设，否则接受原假设。

三、常见的假设检验方法在统计学中，有多种假设检验方法可供选择，下面介绍几种常见的方法：1. 单样本t检验：用于检验一个总体均值是否等于某个给定值。

2. 双样本t检验：用于检验两个总体均值是否相等。

3. 方差分析（ANOVA）：用于检验多个样本的均值是否相等。

4. 卡方检验：用于检验观察频数与期望频数之间的拟合程度。

5. 相关分析：用于检验两个变量之间是否存在线性关系。

（4）计算检测统计量的值
2
n 1 S 2 30 1 2 103.11
02
0.752
（5）作出决策
2 103.11 42.557 ，落入拒绝域，故在 0.05 的显著性水平上拒绝 H 0 。
结论：有证据表明电视的使用寿命的方差显著大于视频录像设备的使用寿命的方差。
2
n=30, S =2, s0 = 0.75 = 0.5625 （1）提出假设
2 2 H0 : 2 0 ; H1 : 2 0
2
2
2
（2）构造检测统计量
n 1 S 2 2 n 1 2
2
0
（3）给定显著性水平 0.05 29 42.557 ，其拒绝域为 42.557, 。
（3）给定显著性水平 0.01 ，确定拒绝域。
0.01 ， z0.01 2.33 ，其拒绝域为 2.33, 。
（4）计算检测统计量的值
z
x 0 7.25 6.70 3.11 s / n 2.5 / 200
（5）作出决策
z 3.11 2.33 ，落入拒绝域，故在 0.01 的显著性水平上拒绝 H 0 。
np 356 0.879 313 5 ， np 1 p 356 0.879 1 0.879 37.81 5 。
本题为大样本下总体比例的双侧检验问题，应采取 Z 检验法。 （1）已知本题假设为
H 0 : 0.75; H1 : 0.75
n
p 0

0.879 0.75 0.75 1 0.75 356
5.63
（5）作出决策