下载文档原格式
数理统计基本概念与假设检验(doc 77页)数理统计与Matlab讲义宋向东目录第1章数理统计基本概念 (1)1.1 总体与样本 (1)1.1.1 简单随机样本 (1)1.1.2 有限总体的无放回样本 (3)1.2 统计量 (3)1.2.1 样本k阶矩 (3)1.2.2 顺序统计量 (4)1.2.3 经验分布函数 (4)1.3 三个常用分布 (6)1.3.1 2 分布 (6)1.3.2 t分布 (7)1.3.3 F分布 (8)第2章参数估计 (10)2.1 点估计 (10)2.1.1 无偏性 (10)2.1.2 有效性 (12)2.1.3 相合性 (12)2.2 区间估计 (13)2.2.1 单正态总体均值的置信区间 (13)2.2.2 单正态总体方差的置信区间 (14)2.2.3 两正态总体均值差的置信区间 (15)2.2.4 两正态总体方差比的置信区间 (15)第3章假设检验 (17)3.1 假设检验的基本概念 (17)3.2 正态总体参数的假设检验 (19)3.2.1 单正态总体均值的假设检验 (19)3.2.2 单正态总体方差的假设检验 (20)3.2.3 两正态总体均值的假设检验 (21)3.2.4 两正态总体方差的假设检验 (21)3.2.5 大样本非正态总体均值的假设检验 (22)3.3 三个常用的非参数检验 (23)3.3.1 符号检验 (23)3.3.2 Wilcoxon秩和检验 (25)3.3.3 Wilcoxon符号秩检验 (30)3.4 检验的功效函数 (32)3.5 总体分布的假设检验 (37)3.5.1 2 检验 (37)3.5.2 Kolmogorov检验 (40)第4章回归分析 (44)4.1 一元回归分析 (44)4.1.1 回归方程的计算 (44)4.1.2 回归方程的显著性检验 (45)4.2 多元回归分析 (48)4.2.1 多元回归方程的计算 (48)4.2.2 显著性检验 (49)4.2.3 逐步回归分析 (52)第5章方差分析 (57)5.1 单因素方差分析 (57)5.1.1 方差分析的基本概念 (57)5.1.2 单因素方差分析的计算 (60)5.1.3 单因素方差分析的多重比较 (65)5.2 双因素方差分析 (67)5.2.1 有重复实验的双因素方差分析 (67)5.2.2 无重复实验的双因素方差分析 (72)参考文献 (76)第1章 数理统计基本概念1.1 总体与样本总体：研究对象的全体。
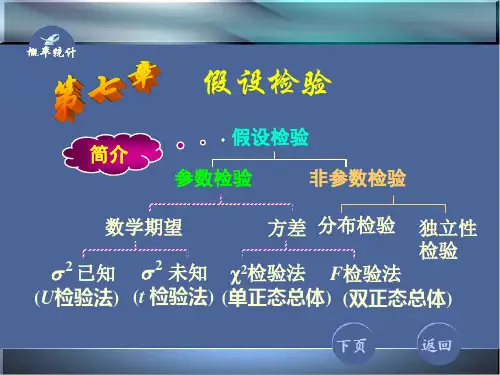
假设检验假设检验(Hypothesis Testing)是数理统计学中根据一定假设条件由样本推断总体的一种方法。
具体作法是：根据问题的需要对所研究的总体作某种假设，记作H0；选取合适的统计量，这个统计量的选取要使得在假设H0成立时，其分布为已知；由实测的样本，计算出统计量的值，并根据预先给定的显著性水平进行检验，作出拒绝或接受假设H0的判断。
常用的假设检验方法有u—检验法、t检验法、χ2检验法(卡方检验)、F—检验法，秩和检验等。
中文名假设检验外文名 hypothesis test提出者 K.Pearson 提出时间 20世纪初1、简介假设检验又称统计假设检验（注：显著性检验只是假设检验中最常用的一种方法），是一种基本的统计推断形式，也是数理统计学的一个重要的分支，用来判断样本与样本，样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。
其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。
[1]2、基本思想假设检验的基本思想是小概率反证法思想。
小概率思想是指小概率事件（P<0.01或P<0.05）在一次试验中基本上不会发生。
反证法思想是先提出假设(检验假设H0)，再用适当的统计方法确定假设成立的可能性大小，如可能性小，则认为假设不成立，若可能性大，则还不能认为假设成立。
[2] 假设是否正确，要用从总体中抽出的样本进行检验，与此有关的理论和方法，构成假设检验的内容。
设A是关于总体分布的一项命题，所有使命题A成立的总体分布构成一个集合h0，称为原假设(常简称假设)。
使命题A不成立的所有总体分布构成另一个集合h1，称为备择假设。
如果h0可以通过有限个实参数来描述，则称为参数假设，否则称为非参数假设(见非参数统计)。
如果h0(或h1)只包含一个分布，则称原假设(或备择假设)为简单假设，否则为复合假设。
对一个假设h0进行检验，就是要制定一个规则，使得有了样本以后，根据这规则可以决定是接受它（承认命题A正确），还是拒绝它（否认命题A正确）。
