吉林省舒兰市第一中学高中数学 2.3.3空间中的角导学案 新人教A版必修2

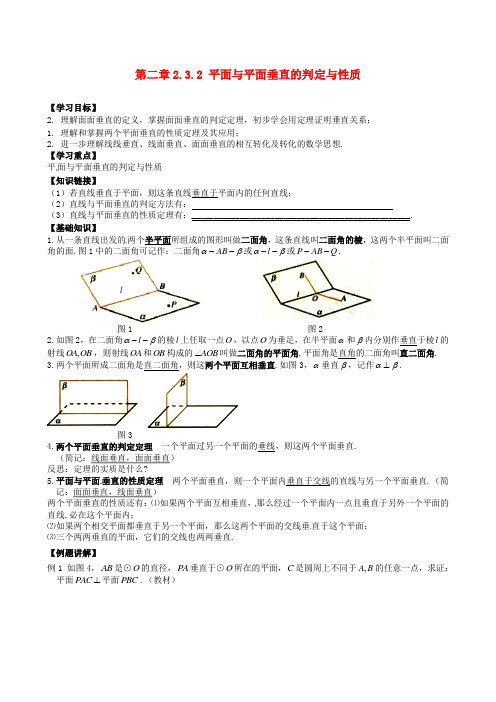
第二章2.3.2 平面与平面垂直的判定与性质【学习目标】2. 理解面面垂直的定义，掌握面面垂直的判定定理，初步学会用定理证明垂直关系； 1. 理解和掌握两个平面垂直的性质定理及其应用；2. 进一步理解线线垂直、线面垂直、面面垂直的相互转化及转化的数学思想. 【学习重点】平面与平面垂直的判定与性质 【知识链接】（1）若直线垂直于平面，则这条直线垂直于平面内的任何直线；（2）直线与平面垂直的判定方法有：（3）直线与平面垂直的性质定理有：__________________________________________________. 【基础知识】1.从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫二面角的棱，这两个半平面叫二面角的面.图1中的二面角可记作：二面角AB αβ--或l αβ--或P AB Q --.图1 图22.如图2，在二面角l αβ--的棱l 上任取一点O ，以点O 为垂足，在半平面α和β内分别作垂直于棱l 的射线,OA OB ，则射线OA 和OB 构成的AOB ∠叫做二面角的平面角.平面角是直角的二面角叫直二面角.3.两个平面所成二面角是直二面角，则这两个平面互相垂直.如图3，α垂直β，记作αβ⊥.图34.两个平面垂直的判定定理 一个平面过另一个平面的垂线，则这两个平面垂直. （简记：线面垂直，面面垂直） 反思：定理的实质是什么?5.平面与平面垂直的性质定理 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直.（简记：面面垂直，线面垂直）两个平面垂直的性质还有：⑴如果两个平面互相垂直，那么经过一个平面内一点且垂直于另外一个平面的直线,必在这个平面内；⑵如果两个相交平面都垂直于另一个平面，那么这两个平面的交线垂直于这个平面； ⑶三个两两垂直的平面，它们的交线也两两垂直. 【例题讲解】例1 如图4，AB 是⊙O 的直径，PA 垂直于⊙O 所在的平面，C 是圆周上不同于,A B 的任意一点，求证：平面PAC ⊥平面PBC .（教材）l图4例2如图5，已知平面,αβ，αβ⊥，直线a 满足a β⊥，a α⊄，求证：a ∥面α.图5例3 如图6，平面α⊥平面γ，βγ⊥平面平面，l αβ=I ，求证：l γ⊥.（教材73页5题）图6【达标检测】1. 对于直线,m n ,平面,αβ,能得出αβ⊥的一个条件是（ C ）. A.,//,//m n m n αβ⊥ B.,,m n m n αβα⊥=⊂I C.//,,m n n m βα⊥⊂ D.//,,m n m n αβ⊥⊥2. 下列命题错误的是（ A ）.A.αβ⊥⇒α内所有直线都垂直于βB.αβ⊥⇒α内一定存在直线平行于βC.α不垂直β⇒α内不存在直线垂直βD.α不垂直β⇒α内一定存在直线平行于β3. 已知αβ⊥，下列命题正确个数有（ C ）. ①αβ内的已知直线必垂直于内的任意直线②αβ内的已知直线必垂直于内的无数条直线 ③α内的任一直线必垂直于βA.3B.2C.1D.04. 已知αβ⊥，,a b αβ⊂⊂，b 是α的斜线，a ⊥b ，则a 与β的位置关系是（ C ）. A.a ∥β B. a 与β相交不垂直 C. a β⊥ D.不能确定5. 若平面αβ⊥平面，直线a α⊂，则a 与β的位置关系为相交或平行或在面内.6. 直线m 、n 和平面α、β满足m n ⊥，m α⊥,αβ⊥，则n 和β的位置关系为相交或平行或在面内.7. 如图8，,,CD CD AB αββ⊥⊂⊥，CE ,EF ⊂α，90FEC ∠=°，求证：面EFD ⊥面DCE .图88. 如图9，AC ⊥面BCD ，BD CD ⊥，设ABC ∠=1θ，2CBD θ∠=，3ABD θ∠=，求证：312cos cos cos θθθ=图9βαD F EC B A。

第三章 3.1.2 两条直线平行与垂直的判定 【学习目标】理解并掌握由直线斜率判断直线位置关系的方法。

【学习重点】通过直线斜率，判断两条直线的位置关系【知识链接】直线的倾斜角为α，则此直线的斜率=k αtan .当α______时，k>0； 当α______时，k=0；当α______时，k<0； 当α______时，k 不存在【基础知识】21//l l 时，21k k 与满足什么关系？21k k =时，21l l 与位置关系如何？21l l 与垂直，则21k k 与满足什么关系？121-=k k 时，21l l 与位置关系如何？【例题讲解】例1 已知A （2，3），B （－4，0），P （－3，１），Q （－1，2），判断直线BA 与P Ｑ的位置关系，并证明你的结论.变式迁移1 若A( -2,3),B(3,-2),C(21,m)三点共线，则m 的值为( )A.21 B.-21 C.-2 D.2 分析：k AB =k BC ,32122332-+=+--m ,m=21. 答案：A例2 已知四边形ABCD 的四个顶点分别为A （0，0），B （2，-1），C(4,2),D(2,3),试判断四边形ABCD 的形状，并给出证明.变式迁移2直线1l ：ax+3y+1=0，2l ：x+(a-2)y+a=0，它们的倾斜角及斜率依次分别为21,αα，21,k k （1）a=_____________时， 1α=150°；（2）a=_____________时，2l ⊥x 轴；（3）a=_____________时，21//l l ；（4）a=_____________时，21,l l 重合；（5）a=_____________时，21l l ⊥ 答案：（1）3 （2）2 （3）3 （4）-1 （5）1.5 例3．判断以A (－1,1)，B (2，－1)，C (1,4)为顶点的三角形的形状.k AB ＝－1－12－－1＝－23. k AC ＝4－11－－1＝32， 由k AB ·k AC ＝－1知三角形是以A 点为直角顶点的直角三角形．【达标检测】1．下列说法正确的有(A )①若两条直线的斜率相等，则这两条直线平行；②若l 1∥l 2.则k 1＝k 2；③若两条直线中有一条直线的斜率不存在，另一条直线的斜率存在，则这两条直线垂直；④若两条直线的斜率都不存在且两直线不重合，则这两条直线平行．A ．1个B ．2个C ．3个D ．4个2．过点A (1,2)和点B (－3,2)的直线与x 轴的位置关系是( B )A ．相交B ．平行C ．重合D ．以上都不对3．经过(m,3)与(2，m )两点的直线l 与斜率为－4的直线互相垂直，则m 的值为(D )A ．－75 B.75C ．－145 D.1454．设点P (－4,2)，Q (6，－4)，R (12,6)，S (2,12)，下面四个结论：①PQ∥SR ；②PQ ⊥PS ；③PS∥QS ；④RP ⊥QS .正确的个数是( C )A ．1B ．2C ．3D ．45．过点A (0，73)，B (7,0)的直线l 1与过点C (2,1)，D (3，k ＋1)的直线l 2和两坐标轴围成的四边形内接于一个圆，则实数k 等于( B )A ．－3B ．3C ．－6D ．66．已知直线l 1的斜率为3，直线l 2过点A (1,2)，B (2，a )．若l 1∥l 2，则a 值为____5 ____；若l 1⊥l 2，则a 值为___53_____． 7．已知M (1，－3)，N (1,2)，P (5，y )，且∠NMP ＝90°，则log 8(7＋y )＝___23_____. 8．已知A (2,3)，B (1，－1)，C (－1，－2)，点D 在x 轴上，则当点D 坐标为(－9,0) 时，AB ⊥CD .9．(12分)当m 为何值时，过两点A (1,1)，B (2m 2＋1，m －2)的直线：(1)倾斜角为135°；(2)与过两点(3,2)，(0，－7)的直线垂直；(3)与过两点(2，－3)，(－4,9)的直线平行．解：(1)由k AB ＝m －32m2＝tan135°＝－1. 解得m ＝－32，或m ＝1. (2)由k AB ＝m －32m 2，且－7－20－3＝3， 则m －32m 2＝－13，解得m ＝32，或m ＝－3. (3)令m －32m 2＝9＋3－4－2＝－2， 解得m ＝34，或m ＝－1. 10．(13分)已知在▱ABCD 中，A (1,2)，B (5,0)，C (3,4)．(1)求点D 的坐标；(2)试判断▱ABCD 是否为菱形？解：(1)设D (a ，b )，由▱ABCD ，得k AB ＝k CD ，k AD ＝k BC ，即⎩⎪⎨⎪⎧ 0－25－1＝b －4a －3，b －2a －1＝4－03－5，解得⎩⎪⎨⎪⎧ a ＝－1，b ＝6，所以D (－1,6)．(2)∵k AC ＝4－23－1＝1，k BD ＝6－0－1－5＝－1， ∴k AC ·k BD ＝－1，∴AC ⊥BD .∴▱ABCD 为菱形．【问题与收获】。

第四章 4.1 圆的方程 编号041【学习目标】１．把握圆的标准方程的特点，能依据所给有关圆心、半径的具体条件精确 地写出圆的标准方程，能运用圆的标准方程正确地求出其圆心和半径，解决一些简洁的实际问题．２．通过圆的标准方程的推导，培育同学利用求曲线的方程的一般步骤解决一些实际问题的力量．３．通过圆的标准方程，解决一些如圆拱桥的实际问题，说明理论既来源于实践，又服务于实践，可以适时进行辩证唯物主义思想训练．【学习重点】(1)圆的标准方程的推导步骤；(2)依据具体条件正确写出圆的标准方程． 【学问链接】（1）圆的定义；（2）直线方程的定义，直线上点的坐标与直线方程解得关系。

【基础学问】探究一：如何建立圆的标准方程呢？1．建系设点： 2．写点集： 3．列方程： 4．化简方程：探究二：圆的方程形式有什么特点？当圆心在原点时，圆的方程是什么？【例题讲解】例1： 写出下列各圆的方程：(1)圆心在原点，半径是3； （2）圆心在C(3,4),半径为5 (3)经过点P(5，1)，圆心在点C(8，-3)； 变式训练１： 说出下列圆的圆心和半径：(1)5)2()3(22=-+-y x ；(2)7)3()4(22=+++y x ；(3)4)2(22=+-y x例２： (1)已知两点P (4，9)和P (6， 3)，求以PP 为直径的圆的方程；(2)试推断点M(6，9)、N(3，3)、Q(5，3)是在圆上，在圆内，还是在圆外？【基础学问】问题1．方程222410x y x y +-++=表示什么图形？方程222460x y x y +-++=表示什么图形？问题2．方程220x y Dx Ey F ++++=在什么条件下表示圆？新知：方程220x y Dx Ey F ++++=表示的轨迹. ⑴当2240D E F +->时，表示以(,)22D E --为圆心,22142D E F +-为半径的圆；⑵当2240D E F +-=时，方程只有实数解2D x =-，2E y =-，即只表示一个点（-2D ，-2E ）;（3）当2240D E F +-<时，方程没有实数解，因而它不表示任何图形小结：方程220x y Dx Ey F ++++=表示的曲线不肯定是圆只有当2240D E F +->时，它表示的曲线才是圆，形如220x y Dx Ey F ++++=的方程称为圆的一般方程思考：1．圆的一般方程的特点？2．圆的标准方程与一般方程的区分？例3：推断下列二元二次方程是否表示圆的方程？假如是，恳求出圆的圆心及半径.⑴224441290x y x y +-++=； ⑵2244412110x y x y +-++=例4 ：已知线段AB 的端点B 的坐标是(4,3)，端点A 在圆上()2214x y ++=运动，求线段AB 的中点M 的轨迹方程.【达标检测】１．圆(x ＋1)2+(y －2)2=4的圆心、半径是 （ D ）A ．(1,－2),4B ．(1,－2),2C ．(－1,2),4D ．(－1,2),2２．过点A(4,1)的圆C 与直线10x y --=相切于点B(2,1)，则圆C 的方程为2)3(22=+-y x 3．一个等腰三角形底边上的高等于5，底边两端点的坐标是(-4，0)和(4，0)，求它的外接圆的方程．4．圆2)1()1(22=++-y x 的周长是（ C ） Ａ．π2 Ｂ．π2 Ｃ．２π2 Ｄ．π45．点Ｐ（5,2m ）与圆2422=+y x 的位置关系是( A ) Ａ．在圆外 Ｂ．在圆内 Ｃ．在圆上 Ｄ．不确定6．已知圆Ｃ与圆1)1(22=+-y x 关于直线x y -=对称，则圆Ｃ的方程为（ C ） Ａ1)1(22=++y x Ｂ．122=+y x Ｃ．1)1(22=++y x Ｄ．1)1(22=-+y x 7．已知圆C 的圆心是直线x-y+1=0与x 轴的交点，且圆C 与直线x+y+3=0相切，求圆C 的方程.2)1(22=++y x8.已知圆心在x的圆O 位于y 轴左侧，且与直线x+y=0相切，求圆O 的方程.2)2(22=++y x9．方程x 2＋y 2－2(m ＋3)x ＋2(1－4m 2)y ＋16m 4+9=0表示圆，则实数m 的取值范围是（ A ）Ａ．－71＜m ＜1 Ｂ．－1＜m ＜71 Ｃ．m ＜－71或m ＞1 Ｄ．m ＜－1或m ＞7110．方程x 2＋y 2＋Dx ＋Ey ＋F =0（D 2＋E 2－4F ＞0）表示的曲线关于直线x ＋y =0对称，则有（ A ） Ａ．D ＋E =0 Ｂ．D ＋F =0 Ｃ．E ＋F =0 Ｄ．D ＋E ＋F =0 11．经过三点A (0，0)、B (1，0)、C (2，1)的圆的方程为（ D ） Ａ．x 2＋y 2＋x －3y －2=0 Ｂ． x 2＋y 2＋3x ＋y －2=0 Ｃ． x 2＋y 2＋x ＋3y =0 Ｄ． x 2＋y 2－x －3y =0 12．方程220x y x y k +-++=表示一个圆，则实数k 的取值范围是21<k .13．过点A （－2，0），圆心在（3，－2）的圆的一般方程为0164622=-+-+y x y x . 14．等腰三角形的顶点是A(4，2)，底边一个端点是B(3，5)，求另一个端点的轨迹方程，并说明它的轨迹是什么．轨迹方程是)5,3(0104822≠≠=+--+x x y x y x 轨迹是以A 为圆心10为半径的圆但除去两点【问题与收获】。

第二章 2.1.1 平面【学习目标】(1 )正确理解平面的几何概念 ,利用生活中的实物对平面进行描述 ,掌握平面的性质 .(2 )熟练掌握三种语言的转换 ,会用三个公理证明共点共线共面的问题 .(3 )掌握平面的表示法及水平放置的直观图；培养学生的空间想象能力 .【学习重点】理解平面的几何概念 ,掌握平面的性质 ,会用三个公理证明共点共线共面的问题【根底知识】无限延展的____的 ,我们通常把水平的平面画成一个_ 平行四边形___ .2.常用符号的记法：(1 )点A 在平面α内 ,记作__α∈A ____；点B 在平面α外 ,记作__α∉B ____ . (2 )点P 在直线上 ,记作____l P ∈___；点P 在直线l 外 ,记作_____l P ∉_____ .(3 )直线l 在平面α内 ,记作__α⊂l ___；直线l 不在平面α内 ,记作___α⊄l ____ .3.公理1:如果_一条直线上的两点在一个平面内__ ,那么这条直线在此平面内 .用符号表示为____________________ ,图形为________________,其作用是_证明直线在平面内____ .4.公理2:__过不在一条直线上的__的三点 ,_有且只有_____一个平面 .图形为_________________________ ,其作用是___确定平面___________ .推论1.经过一条直线和这条直线外一点,有且只有一个平面.推论2.经过两条相交直线,有且只有一个平面.推论3.经过两条平行直线,有且只有一个平面.5.公理3:如果两个不重合的平面 有一个公共点 ,那么它们_有且只有一条过该点____的公共直线 .用符号表示为_________________________ ,图形为___________________ ,其作用是___做两个平面的交线_____ .注意： (1 )公理中 "有且只有一个〞的含义是： "有〞 ,是说图形存在 , "只有一个〞 ,是说图形唯一 ,"有且只有一个平面〞的意思是说 "经过不在同一直线上的三个点的平面是有的 ,而且只有一个〞 ,也即不共线的三点确定一个平面. "有且只有一个平面〞也可以说成 "确定一个平面.〞(2 )过A 、B 、C 三点的平面可记作 "平面ABC 〞【例题讲解】例1：用符号表示以下图形中点、直线、平面之间的关系 .变式迁移1：用符号表示以下语句 ,并画出相应的图形 .(1 )点A 在平面α内 ,但点B 在平面α外； (2 )直线a 经过平面α外的一点M ；α β A B a l P α β l a b(3 )直线a 既在平面α内 ,又在平面β .例2 以下命题正确的选项是( C )A ．画一个平面 ,使它的长为 14 cm ,宽为 5 cmB ．一个平面的面积可以是 16 2mC ．平面内的一条直线把这个平面分成两局部 ,一个平面把空间分成两局部D ．10 个平面重叠起来 ,要比 2 个平面重叠起来厚例3 以下命题正确的选项是( D )A ．经过三点确定一个平面B ．经过一条直线和一个点确定一个平面C ．四边形确定一个平面D ．两两相交且不共点的三条直线确定一个平面例4 判断以下命题是否正确A ．平面α与平面β相交 ,它们只有有限个公共点 . ( × )B ．经过一条直线和这条直线外的一点 ,有且只有一个平面 ( √ )C ．经过两条相交直线 ,有且只有一个平面 ( √ )D ．如果两个平面有三个不共线的公共点 ,那么这两个平面重合 ( √ )【达标检测】1. 三条不同的直线a,b,c 两个不同的点A ,B 及面α ,如果a B b l A a l b a =⋂=⋂⊂⊂,,,α 那么以下关系成立的是 ( A )A ．α⊂l B.α⊄l C.A l =⋂α D.B l =⋂α 2.空间四点A ,B ,C ,D 共面但不共线 ,那么这四点中 ( B )A.必有三点共线3.互不重合的三个平面最|多可以把空间分成的局部是 ( D )A. 4B. 5C. 7D. 84.下面给出了四个条件： (1 )空间三个点 (2 )一条直线和一个点 (3 )和直线a 都相交的两条直线； (4 )两两相交的三条直线.其中 ,能确定一个平面的条件有 ( A )A ．0个 B. 1个 C. 2个 D. 3个四边形ABCD 的边AB ,BC ,CD ,DA 上分别取E ,F ,G ,H 四点 ,如果EF 与HG 交于点M ,那么 ( A )A ．C ．M 可能在直线AC 上 ,也可能在直线BD 上D ．M 既不在直线AC 上 ,也不在直线BD 上6.A ,B ,C 表示不同的点 ,l a ,表示不同的直线 ,βα,表示不同的平面 ,以下推理不正确的选项是 ( C )A ．ααα⊂⇒∈∈∈∈lB l B A l A ,,,B ．=⋂⇒∈∈∈∈βαβαβαB B A A ,,,直线ABC ．αα∉⇒∈⊄A l A l ,D ．A ,B ,C βα∈∈C B A ,,,且A ,B ,C 不共线βα与⇒重合7. 以下命题正确的选项是( C )A ．因为直线向两方无限延伸 ,所以直线不可能在平面内B ．如果线段的中点在平面内 ,那么线段在平面内C ．如果线段上有一个点不在平面内 ,那么线段不在平面内D ．当平面经过直线时 ,直线上可以有不在平面内的点8.在空间 ,以下命题中不正确的选项是 ( B )A.如果两个平面有一个公共点 ,那么它们还有其他公共点B.假设四个点不共面 ,那么其中任意三个点也不共面平面α内又在平面β内 ,那么点A 在平面α与平面β的交线上D.假设两点A ,B 既在直线l 上又在平面α内 ,那么l 在平面α内9.假设直线上有两个点在平面外 ,那么 ( D )A.直线上至|少有一个点在平面内D.直线上至|多有一个点在平面内10.给出以下说法： (1 )梯形的四个顶点共面； (2 )三条平行直线共面 (3 )有三个公共点的两个平面重合 (4 )每两条都相交并且交点全部不同的四条直线共面 ,其中说法正确的序号是 ( ( 1)(.4 ) )11.M ,N ,P ,Q 分别是正方体ABCD -1111D C B A 中棱AB ,BC ,C C D C 111,的中点 ,证明：M ,N ,P ,Q 四点共面 .。

第二章 2.2. 2 平面与平面平行的判定与性质【学习目标】1.能借助于长方体模型讨论直线与平面、平面与平面的平行问题；2.理解和掌握两个平面平行的判定定理及其运用；3.掌握两个平面平行的性质定理；4.灵活运用面面平行的判定定理和性质定理，掌握“线线、线面、面面”平行的转化.【学习重点】平面与平面平行的判定与性质【知识链接】1：直线与平面平行的判定定理是 平面外一条直线与此平面内的一条直线平行 ，则该直线与此平面平行. 2：两个平面的位置关系有 两 种，分别为_平行_和_相交_.【基础知识】1.两个平面平行的判定定理 一个平面内的两条相交直线与另一个平面平行，则这两个平面平行. （简记：线面平行，面面平行）反思：⑴定理的实质是什么?⑵用符号语言把定理表示出来.⑶如果要证明定理，该怎么证明呢？ 2.判定平面与平面平行通常有5种方法⑴根据两平面平行的定义(常用反证法)；⑵根据两平面平行的判定定理；⑶垂直于同一条直线的两个平面平行(以后学习)；⑷两个平面同时平行于第三个平面，则这两个平面平行(平行的传递性)；⑸一个平面内的两条相交直线分别平行于另外一个平面内的两条相交直线，则这两个平面平行(判定定理的推论. 简记：线线平行，面面平行).3.两个平面平行的性质定理 如果两个平行平面同时和第三个平面相交，那么它们的交线平行. （简记：面面平行，线线平行）反思：⑴定理的实质是什么?⑵用符号语言把定理表示出来.⑶如果要证明定理，该怎么证明呢？4.两个平面平行，还有如下结论：⑴如果两个平面平行，则一个平面内的任何直线都平行于另外一个平面（简记：面面平行，线面平行）；⑵夹在两个平行平面内的所有平行线段的长度都相等；⑶如果一条直线垂直于两个平行平面中的一个，那么这条直线也垂直于另一个平面.⑷如果一条直线和两个平行平面中的一个相交,那么它和另一个也相交.【例题讲解】例1 如图，已知正方体1111ABCD A B C D ，求证：平面11AB D ∥D BC 1.（教材）例2 如图，已知,a b 是两条异面直线，平面α过a ，与b 平行，平面β过b ，与a 平行，求证：平面α∥平面β变式训练1 如图，正方体中，,,,M N E F 分别是棱A B ''，A D ''，B C ''C D ''求证：平面AMN ∥平面EFDB .例3 如图，α∥β，AB ∥CD ，且A α∈，C α∈B β∈，D β∈.求证：AB CD =.【达标检测】1. 平面α与平面β平行的条件可以是（ D ）.A.α内有无穷多条直线都与β平行B.直线a 与,αβ都平行，且不在α和β内C.直线a α⊂,直线b β⊂,且a ∥β,b ∥αD.α内的任何直线都与β平行2. 下列命题错误的是（ D ）.A.平行于同一条直线的两个平面平行或相交B.平行于同一个平面的两个平面平行C.平行于同一条直线的两条直线平行D.平行于同一个平面的两条直线平行或相交3. 经过平面α外的一条直线a 且与平面α平行的平面（ C ）.A.有且只有一个B.不存在C.至多有一个D.至少有一个4. 设有不同的直线,a b ，及不同的平面α、β，给出的三个命题中正确命题的个数是（ B ）. ①若a ∥α,b ∥α,则a ∥b ②若a ∥α,α∥β,则a ∥β③若,a αα⊂∥β,则a ∥β.A.0个B.1个C.2个D.3个5. ,m n 是不重合的直线，,αβ是不重合的平面：①m α⊂，n ∥α，则m ∥n ②m α⊂，m ∥β，则α∥β③n αβ=I ，m ∥n ，则m ∥α且m ∥β 上面结论正确的有（ A ）.βαb a F E M N B 'C ' A 'D C B A D ' D C B A βαA.0个B.1个C.2个D.3个6. 3个平面把空间分成6个部分，则（ D ）.A.三平面共线B.三平面两两相交C.有两平面平行且都与第三平面相交D.三平面共线或者有两平面平行且都与第三平面相交 7. 直线与两个平行平面中的一个平行，则它与另一平面平行或在面内. 8. 一个平面上有不同三点到另一个平面的距离相等，则这两个平面平行或者相交.9. 如果两个平面分别经过两条平行线中的一条，则这两个平面的位置关系是平行或者相交.10. 若两个平面都平行于两条异面直线中的每一条,则这两平面的位置关系是平行.11.如图，在几何体ABC A B C '''-中，1∠+2180∠=°,34180∠+∠=°,求证：平面ABC ∥平面A B C '''.12. 如图，A '、B '、C '分别是PBC ∆、PCA ∆、PAB ∆的重心.求证：面A B C '''∥ABC 面.13. 如图，设,P Q 是单位正方体1AC 的面11AA D D 、面1111A B C D 的中心，证明：⑴PQ ∥平面11AA B B ；⑵面1D PQ ∥面1C DB .【问题与收获】。

吉林省舒兰市第一中学高中地理第二章第一节城市内部空间结构导学案新人教版必修2【学习目标】1、理解城市土地利用方式及功能分区2、掌握影响城市地域结构的主要因素3、科学地看待城市地域结构的发展【教学重点】城市的空间结构及其形成原因【教学难点】1、城市的空间结构及其形成原因2、科学地看待城市地域结构的发展【知识链接】（一）城市土地利用和功能分区1、城市土地利用方式有哪些？2、同一种土地利用方式对用地空间和位置需求往往是_________，这就会导致同一类活动在城市空间上的________，形成各种_________。

3、功能区特点：（1）之间无___________________；（2）内部兼有_____________________。

4、住宅区（1）最广泛的土地利用方式，占据城市空间的_____________。

（2）出现了_____________和______________的分化。

5、商业区（1）位置：________________________________________，主要为状分布。

（2）CBD 多分布在大城市和特大城市的市中心。

6、工业区工业布局位置：____________________________________。

7、其他功能区如：，多分布在大城市。

（二）、城市内部空间结构的形成和变化1、什么是城市地域结构？2、城市地域结构三种模式：【自主预习】1、城市地域结构、城市功能区与城市形态的区别：城市地域结构是指在经济、社会、历史和政策等因素作用下，城市功能分区在空间上的分布组合；而城市地域功能分区是指城市中各种经济活动之间发生空间竞争，会导致同类活动在空间上的高度集聚所形成的商业区，工业区和住宅区等；城市形态是指整个城市的外部形态。

其关系如下图所示：分布组合外部形态城市功能区城市地域结构城市形态城市形态成都合肥华盛顿重庆市兰州市、洛阳西宁、宜昌延安市类型团块状组团状条带状放射式影响因素位于平坦开阔的平原地区受山丘、河流或交通线的分割沿着河流、山谷或交通线向两头延伸位于多条河流或交通线的交汇处优点便于集中设置完善的服务设施，便于行政管理，节省建设投资分散生产，分散管理，环境污染较小各个部分接近郊区，亲近自然，环境污染较小各个部分接近郊区，亲近自然，环境污染较小缺点集中分布容易产生生产和生活污染等环境问题，不利于扩建用地比较分散，联系不方便，市政工程设施投资相对要高集中于两个方向，两头运距很长，不便于行政管理，建设投资较大集中于三个方向，三投运距很长，不便于行政管理，建设投资较大。

第二章 2.1.2 空间中直线与直线之间的位置关系编号030【学习目标】1.理解异面直线的概念；了解空间中两条直线的三种位置关系，知道异面直线、异面直线的夹角以及直线垂直的概念；2.能正确理解平行公理和等角定理，并会运用进行相关的推理证明。

3.通过对比空间和平面两直线间的位置关系之间异同和联系，逐步提高将立体图形转为平面图形的能力以及空间想象能力、观察归纳能力、类比推理能力．【学习重点】重点：异面直线的概念及异面直线所成的角的概念及异面直线所成的角求法难点：理解异面直线概念，作异面直线所成的角.【知识链接】以长方体为载体，使学生在直观感知的基础上，认识空间中两直线的位置关系；通过“直观感知——操作确认——思维辩证”的认知过程展开，得到平行公理和等角定理．【基础知识】复习1：平面的特点是______、_______ 、_______.复习2：平面性质(三公理)公理1_________________________________________________________________；公理2_________________________________________________________________；公理3_________________________________________________________________.探究1：异面直线及直线间的位置关系问题：平面内两条直线要么平行要么相交（重合不考虑）,空间两条直线呢?观察：如图在长方体中，线段A1B所在直线与线段CC1所在直线的位置关系如何？结论：直线与既不相交，也不平行.新知1：像直线A1B与CC1这样不同在任何一个平面内的两条直线叫做异面直线试试：请在上图的长方体中，再找出3对异面直线.问题：作图时，怎样才能表示两条直线是异面的？新知2：异面直线的画法有如下几种(异面)：理解选择合适的异面直线的定义：不同在任何一个平面内的两条直线叫做异面直线。

第二章 空间中的角【学习目标】掌握空间中的三种角的概念及范围；能够在图形中找出或者做出所求角 ,并能在三角形中进行计算.【学习重点】空间中的角度的计算【知识链接】1. 异面直线：不同在任何一个平面内的两条直线叫做异面直线2.等角定理：空间中如果两个角的两边分别对应平行 ,那么这两个角相等或互补.【根底知识】图11.如图1,两条异面直线,a b ,经过空间任一点O 作直线 a '∥a ,b '∥b ,把a '与b '所成的锐角(或直角)叫做异面直线,a b 所成的角(夹角).如果两条异面直线所成的角是直角 ,就说这两条直线互相垂直 ,记作a b ⊥.反思：思考以下问题.(1 )作异面直线夹角时 ,夹角的大小与点O 的位置有关吗?点O 的位置怎样取才比拟简便?(2 )异面直线所成的角的范围是多少?(3 )两条互相垂直的直线一定在同一平面上吗?(4 )异面直线的夹角是通过什么样的方法作出来的?它表达了什么样的数学思想?(5 )异面直线的判定定理：过平面外一点与平面内一点的直线 ,和平面内不经过该点的直线是异面直线.2. 直线PA 和平面α相交但不垂直 ,PA 叫做平面的斜线 ,PA 和平面的交点A 叫斜足；PO α⊥ ,AO 叫做斜线PA 在平面α上的射影.平面的一条斜线和它在平面上的射影所成的锐角 ,叫这条直线和平面所成的角.直线垂直于平面 ,那么它们所成的角是直角；直线和平面平行或在平面内 ,那么它们所成的角是0°角. 反思：求直线与平面所成的角关键是：在斜线上选出一特殊点 ,做出其在平面内的射影.确定点的射影位置的方法有①斜线上任意一点在平面上的射影必在斜线在平面内的射影上②一个点到一个角的两边距离相等 ,那么这个点的射影在这个角的角平分线上 (射影在角分线定理 ) ③假设两个面垂直 ,那么一个面上的点在另一面上的射影必在两个平面的交线上.④面面垂直的性质定理.半平面所组成的图形叫做二面角 ,这条直线叫二面角的棱 ,这两个半平面叫二面角的面.图1中的二面角可记作：二面角AB αβ--或l αβ--或P AB Q --.图1 图2如图2 ,在二面角l αβ--的棱l 上任取一点O ,以点O 为垂足 ,在半平面α和β内分别作垂直于棱l 的射O A P αl线,OA OB ,那么射线OA 和OB 构成的AOB ∠叫做二面角的平面角.平面角是直角的二面角叫直二面角. 反思：⑴两个平面相交 ,构成几个二面角?它们的平面角的大小有什么关系 ?⑵你觉的二面角的大小范围是多少 ?⑶二面角平面角的大小和O 点的选择有关吗 ?除了以上的作法 ,二面角的平面角还能怎么作 ? 小结：求二面角的关键是作出二面角的平面角. 二面角的平面角的一个常用作法：如图过平面α内一点A ,作AB β⊥于点B ,再作BO l ⊥于O ,连接OA ,那么AOB ∠即为所求平面角.(为什么?)【例题讲解】例1 如图 ,在正方体中 ,求以下异面直线所成的角.⑴BA '和CC ' ⑵B D ''和C A '(1 )045 (2 )090例2 如图 ,在正方体中 ,求直线A B '和平面A B CD ''所成的角. 030变式训练1：如图 ,在Rt BMC ∆中 ,斜边5BM = ,其射影4AB = ,60MBC ∠=°090=∠MCB ,求MC 与平面CAB所成角的正弦值.(532)例3 在三棱锥P -ABC 中 ,PA ⊥底面ABC,PA =AB,∠ABC =060,∠BCA =090,点D 、E 分别在棱PB 、PC上 ,且DE//BC. D B 'C 'A ' C B A D '(1) 求证：BC ⊥底面PAC ；(2) 当D 是PB 的中点时 ,求AD 与平面PAC 所成角的正弦值；42 (3) 是否存在点E 使得二面角A -DE -P 为直二面角 ?并说明理由. (存在 ,PC AE ⊥ )【达标检测】1. 以下四个命题 ,正确的选项是 ( D ).C.二面角的平面角是这两个面中直线所成的角中最|小的一个无关2. 在正方体1111ABCD A B C D -中 ,过,,A C D 的平面与过1,,D B B 的平面的位置关系是 ( C ). °角3. 二面角的大小范围是]1800[00，.4. 假设平面内的一条直线和这个平面的一条斜线在平面内的的射影垂直 ,那么它和这条斜线垂直 (三垂线定理 ).5. 假设平面内的一条直线和这个平面的一条斜线垂直 ,那么它和这条斜线在平面内的的射影垂直 (三垂线定理的逆定理 )6. 两条直线和一个平面所成的角相等 ,那么这两条直线的位置关系是 相交、平行或异面 .7. 棱长都相等的正三棱柱ABC -A 1B 1C 1 ,D 是BB 1的中点 , ,求面A 1DC 与面A 1B 1C 1所成的锐二面角的大小为045.8.如图 ,四棱锥P ABCD -的底面是个矩形 ,2,2AB BC == ,侧面PAB 是等边三角形 ,且侧面PAB 垂直于底面ABCD .⑴证明：侧面PAB ⊥侧面PBC ； ⑵求侧棱PC 与底面ABCD 所成的角. (045 )D C BA P9.在四棱锥P -ABCD中 ,底面ABCD为平行四边形 ,∠ADC =045 ,AD =AC =1 ,O为AC的中点 ,PO⊥平面ABCD,PO =2 ,M为PD的中点.(1)求证：PB//平面ACM;(2)证明AD⊥平面PAC;(3)求直线AM与平面ABCD所成角的正切值.(554) 【问题与收获】。

第二章直线与平面平面与平面的位置关系【学习目标】, ,平面与平面之间的位置关系.2.进一步熟悉文字语言、图形语言、符号语言的相互转换.3.进一步培养学生的空间想象能力.【学习重点】1.正确判定直线与平面的位置关系.2.平面与平面的相交和平行.【知识链接】1.什么叫做直线在平面内?直线与平面相交?直线与平面平行?2.直线在平面外包括哪几种情况?3.什么叫做两个平面平行 ?两个平面相交?4.两个平面平行的画法.【根底知识】直线与平面：1.如果直线与平面有无数个公共点叫做直线在平面内.2.如果直线与平面有且只有一个公共点叫做直线与平面相交.3.如果直线与平面没有公共点叫做直线与平面平行.4.直线与平面相交或平行的情况统称为直线在平面外.直线在平面内a α直线与平面相交a∩α =A直线与平面平行a∥α平面与平面：1.两个平面平行 - -没有公共点.2.两个平面相交 - -有一条公共直线.【例题讲解】例1 以下命题中正确的个数是( B )①假设直线l上有无数个点不在平面α内 ,那么l∥α②假设直线l与平面α平行 ,那么l与平面α内的任意一条直线都平行③如果两条平行直线中的一条与一个平面平行 ,那么另一条也与这个平面平行④假设直线l与平面α平行 ,那么l与平面α内的任意一条直线都没有公共点A.0B.1 C例2 α∩β =l,a⊂α,b⊂β,试判断直线a、b的位置关系,并画图表示.解：如下图,直线a、b的位置关系是平行、相交、异面.例3 一条直线与三条平行直线都相交 ,求证：这四条直线共面.直线a∥b∥c ,直线l∩a =A ,l∩b =B ,l∩c =C.求证：l与a、b、c共面.证明：如图1,∵a∥b,图1∴a、b确定一个平面 ,设为α.∵l∩a =A ,l∩b =B,∴A∈α ,B∈α.又∵A∈l ,B∈l,∴AB⊂α ,即l⊂α.同理b、c确定一个平面β ,l⊂β,∴平面α与β都过两相交直线b与l.∵两条相交直线确定一个平面,∴α与β重合.故l与a、b、c共面.例4 三个平面α ,β ,γ.如果α∥β ,γ∩α＝a ,γ∩β＝b ,且直线c⊂β ,c∥b.(1)判断c与α的位置关系 ,并说明理由；(2)判断c与a的位置关系 ,并说明理由．解：(1)c∥α.因为α∥β ,所以α与β没有公共点 ,又c⊂β ,所以c与α无公共点 ,那么c∥α.(2)c∥a.因为α∥β,所以α与β没有公共点 ,又γ∩α＝a,γ∩β＝b,那么a⊂α,b⊂β,且a,b ⊂γ ,所以a ,b没有公共点．由于a ,b都在平面γ内 ,因此a∥b ,又c∥b ,所以c∥a.【达标检测】1.a、b两直线平行于平面α ,那么a、b的位置关系是( D )B.相D.可能平行、可能相交、可能异面2.三条不同的直线a ,b ,c两个不同的点A ,B及面α ,如果a⊂α ,b⊂α ,l∩a＝A ,l∩b＝B ,那么以下关系成立的是(A)A．l⊂α B．l⊄αC．l∩α＝A D．l∩α＝B3.直线a∥b ,b⊂α ,那么a与α的位置关系是( C )A.a∥α⊂α4．a ,b为异面直线是指( D )①a ∩b ＝Ø ,且a 不平行于b ；②a ⊂平面α ,b ⊄平面α ,且a ∩b ＝Ø；③a ⊂平面α ,b ⊂平面β ,且α∩β＝Ø；④不存在平面α能使a ⊂α ,且b ⊂α成立．A ．①②③B ．①③④C ．②③D ．①④5.直线m 与平面α平行的充分条件是( B )A. n ⊂α、m∥nB. m ⊄α、n ⊂α、m∥nC. n ⊂α ,l∥α ,m∥n、m∥lD. n ⊂α ,M∈m 、P ∈m 、N ∈n 、Q ∈n 且MN =P Q6.假设直线a 不平行于平面α,且a ⊄α,那么以下结论成立的是( D )A. α内的所有直线与a 异面B. α内的直线与a 都相交C. α内存在唯一的直线与a 平行D. α内不存在与a 平行的直线7．长方体的12条棱所能确定的平面个数为( C )A ．8B ．10C ．12D ．148．假设P 是两条异面直线l ,m 外的任意一点 ,那么( B )A ．过点P 有且仅有一条直线与l ,m 都平行B ．过点P 有且仅有一条直线与l ,m 都垂直C ．过点P 有且仅有一条直线与l ,m 都相交D ．过点P 有且仅有一条直线与l ,m 都异面9.不在同一条直线上的三点A 、B 、C 到平面α的距离相等 ,且A ∉α,给出以下三个命题：①△ABC 中至|少有一条边平行于α;②△ABC 中至|多有两边平行于α；③△ABC 中只可能有一条边与α相交. 其中真命题是___①__. 10.两个平面把空间分为3或4局部 ,三个平面可以把空间分为 4、6、7、8 局部11.△ABC 的三边或延长线与平面α分别相交于点P ,Q ,R ,那么P ,Q ,R 的位置关系是P ,Q ,R 三点共线．12.a ⊂α,b ⊂α,a∩b =A,P∈b,PQ∥a ,求证：PQ ⊂α.证明：∵PQ∥a ,∴PQ、a 确定一个平面 ,设为β.∴P∈β ,a ⊂β ,P ∉∈α ,a ⊂α ,P ∉a,由推论1：过P 、a 有且只有一个平面,∴α、β重合.∴PQ ⊂α.∴PB 1 =A 1B 1－A 1P =a a a 4341=-. 13.点A 是△BCD 所在平面外一点 ,AD ＝BC ,E ,F 分别是AB ,CD 的中点 ,且EF ＝22AD ,求异面直线AD 和BC 所成的角．解：如图 ,设G 是AC 的中点 ,连接EG ,FG .因E ,F 分别是AB ,CD 的中点 ,故EG∥BC ,且EG ＝12BC ,FG ∥AD ,且FG ＝12AD .由异面直线所成角定义可知EG 与FG 所成锐角或直角为异面直线AD ,BC 所成的角 ,即∠EGF 为所求的角．由BC ＝AD 知EG ＝GF ＝12AD ,又EF ＝22AD, 由勾股定理可得∠EGF ＝90° ,即异面直线AD 和BC 所成的角为90°.【问题与收获】。

其次章2.3.1 直线与平面垂直的判定与性质（老师版） 编号034【学习目标】1. 理解直线与平面垂直的定义；把握直线与平面垂直的判定定理及其应用；2. 理解和把握直线与平面垂直的性质定理及其应用；3.了解反证法证题的思路和步骤；4. 把握平行与垂直关系的转化. 【学习重点】直线与平面垂直的判定定理及性质定理 【学问链接】当两条直线的夹角为090，这两条直线相互垂直；它们的位置关系是相交或异面. 【基础学问】1.假如直线l 与平面α内的任意一条直线都垂直，就说直线l 与平面α相互垂直，记做l α⊥.l 叫做垂线，α叫垂面，它们的交点P 叫垂足.如图所示.2.直线与平面垂直的判定定理 一条线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直（简记：线线垂直，线面垂直）. 判定方法还有：（1）定义法（2）两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面.（3）一条直线垂直于两个平行平面中的一个，那么这条直线也垂直于另一个平面. 3.直线与平面垂直的性质定理（1）一条直线垂直一个平面，那么这条直线垂直于这个平面内的任意直线. （简记：线面垂直，线线垂直）（2）垂直于同一个平面的两条直线平行. （3）过一点仅有一条直线垂直于已知平面 （4）过一点仅有一个平面垂直于已知直线【例题讲解】例1 推断下列命题是否正确，并说明理由.⑴两条平行线中的一条垂直于某条直线，则另一条也垂直于这条直线；（√） ⑵两条平行线中的一条垂直于某个平面，则另一条也垂直于这个平面；（√） ⑶两个平行平面中的一个垂直于某个平面，则另一个也垂直与这个平面；（√） ⑷垂直于同一条直线的两条直线相互平行；（√） ⑸垂直于同一条直线的两个平面相互平行；（√） ⑹垂直于同一个平面的两个平面相互平行. （×） 例2 已知a ∥b ，a α⊥，求证：α⊥b .例3 已知直线a ⊥平面α，直线b ⊥平面α，求证：a ∥b .变式训练1：在三棱锥V-ABC 中，,VA VC AB BC ==，求证：VB AC ⊥.【达标检测】1. 直线l 和平面α内两条直线都垂直，则l 与平面α的位置关系是（ D ）.A.垂直B.平行C.相交但不垂直D.都有可能 2. 下列四个命题中错误的是（ D ）.A.,a b a αα⊥⊥⇒∥bB.,a a α⊥∥b b α⇒⊥C.,a b α⊥∥,a b α⇒⊥D.,a a b b α⊥⊥⇒∥α3. 已知直线,a b 和平面α，下列错误的是（ D ）. A.a ab b αα⊥⎫⇒⊥⎬⊂⎭B.//a b b a αα⎫⇒⊥⎬⊥⎭C.a b b α⊥⎫⇒⎬⊥⎭a ∥α或a α⊂ D.//a b αα⎫⇒⎬⊂⎭a ∥b 4. ,a b 是异面直线,那么经过b 的全部平面（ A ）.A.只有一个平面与a 平行B.有很多个平面与a 平行C.只有一个平面与a 垂直D.有很多个平面与a 垂直5. 平面α外不共线的三点,,A B C 到α的距离都相等，则正确的结论是（ D ）. A.平面ABC 必平行于α B.平面ABC 必垂直于αC.平面ABC 必与α相交D.存在ABC ∆的一条中位线平行于α或在α内 6. 已知平面α和平面β相交,a 是α内一条直线，则有（ B ）.A.在β内必存在与a 平行的直线B.在β内必存在与a 垂直的直线C.在β内不存在与a 平行的直线D.在β内不肯定存在与a 垂直的直线 7. 若平面α∥平面β,直线a ⊥α,则a 与β_垂直_.8. 直线a α⊥，直线b β⊥，且α∥β，则a _//_b .9. 如图，在正方体中，O 是底面的中心，B H D O ''⊥，H 为垂足，求证：B H '⊥面AD C '.10求证：三棱锥有两组对棱垂直，第三组对棱肯定垂直，顶点在底面的摄影是底面三角形的垂心.【问题与收获】。