下载文档原格式
第四章图形的初步认识
§4.2画立体图形
课时一由视图到立体图形
【学习目标】1.会由物体的三视图描绘出物体的形状。
【课前导习】
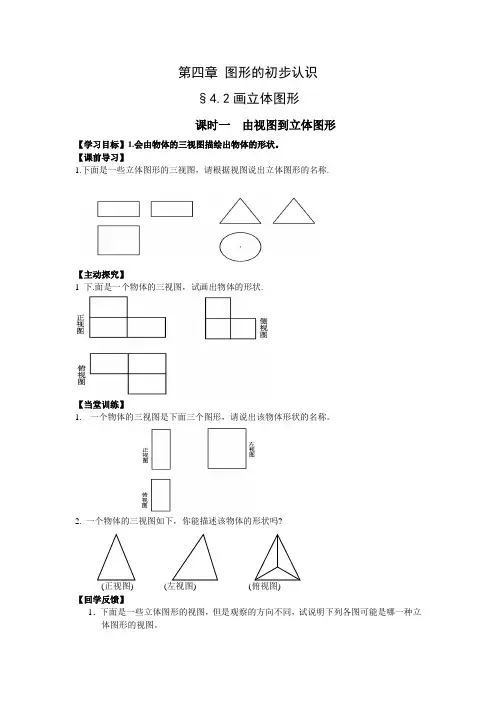
1.下面是一些立体图形的三视图，请根据视图说出立体图形的名称.
【主动探究】
1 下.面是一个物体的三视图，试画出物体的形状.
【当堂训练】
1.一个物体的三视图是下面三个图形，请说出该物体形状的名称。
2.一个物体的三视图如下，你能描述该物体的形状吗?
(正视图) (左视图) (俯视图)
【回学反馈】
1．下面是一些立体图形的视图，但是观察的方向不同，试说明下列各图可能是哪一种立体图形的视图。
2．下面是一物体的三视图，试描述该物体的形状。
怎样将几何的三视图还原为立体几何图形
三视图还原立体几何简单与否因人而异，空间想象力强的人，一眼便能看出是什么样的图形。
我就觉得这种题目还是挺简单的，哈哈。
首先我给你几个最常见的例子。
1.三面都是长方，就是长方体；2.上面看圆，两个侧面看长方，就是圆柱；3.上面看圆，两侧面看三角，就是圆锥；4.上面看多边形，两侧面看三角，就是棱锥；5.上面看多边形，两侧看长方，就是棱柱；6.上面看圆，两侧看梯形，就是圆台；7.三面都是圆，就是球。
其次要注意的是，三视图显示了图形的长宽高，从上方看的图显示了长宽或者直径之类的东西，从侧面看的图显示了长和高，或者宽和高，或者直径和高之类的。
第三要是你空间想象力不强，那么就得多练习。
至于方法，我觉得多锻炼逆向思维能力是最好的。
你可以随便想象出一个立体图形，然后自己给那个图形画三视图，然后再只看你的三视图想象你刚才想的图形，反复练习，多总结，我想你会有启发、收获的。
最后说说三视图的作用。
要是你单看三视图，这个东西高考也不会考，看似没有用，实际上它是很有用的。
它为你以后的立体几何题的分析打下了一定的基础，是一个融入于解题思路中的方法。
综上所述，建议你好好练习三视图。
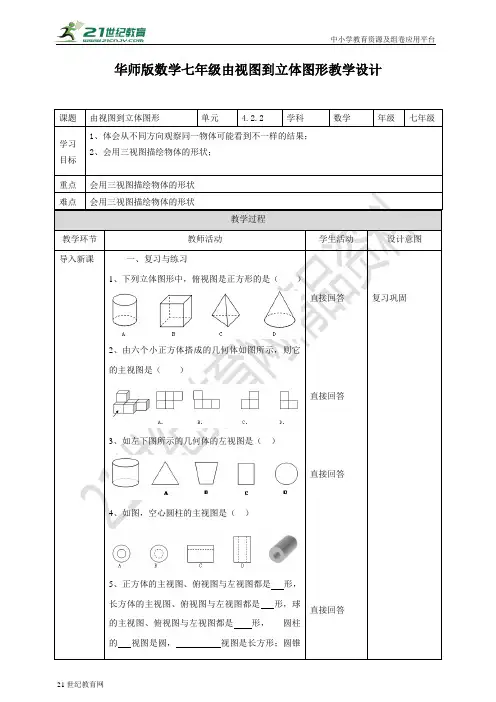
华师版数学七年级由视图到立体图形教学设计课题由视图到立体图形单元 4.2.2 学科数学年级七年级学习目标1、体会从不同方向观察同一物体可能看到不一样的结果；2、会用三视图描绘物体的形状；重点会用三视图描绘物体的形状难点会用三视图描绘物体的形状教学过程教学环节教师活动学生活动设计意图导入新课一、复习与练习1、下列立体图形中，俯视图是正方形的是（）2、由六个小正方体搭成的几何体如图所示，则它的主视图是（）3、如左下图所示的几何体的左视图是（）4、如图，空心圆柱的主视图是（）5、正方体的主视图、俯视图与左视图都是形，长方体的主视图、俯视图与左视图都是形，球的主视图、俯视图与左视图都是形，圆柱的视图是圆，视图是长方形；圆锥直接回答直接回答直接回答直接回答复习巩固的视图是圆，视图是三角形；二、提出问题我们可以画出物体的三视图，那么，我们能不能根据视图来想象物体的形状呢？思考引出新课讲授新课一、例题讲解例1、下图所示的是一些立体图形的三视图，请根据视图说出立体图形的名称。
分析：1、正方体、长方体的三视图有什么特点？2、圆柱和圆锥的三视图有什么特点？解：（1）该立体图形是长方体，如下图所示：（2）该立体图形是圆锥，如下图所示：例2、下图是一个物体的三视图，试想象该物体的形状。
交流讨论直接回答引导学生观察、思考、想象逆向思考分析：1、从府视图可以知道每层最多几个正方体？2、从主视图能看出层数是几，每层的大致左右排面情况？3、从左视图可以明确每层前后排面情况？解：由俯视图得，正方体有2行2列，第一行第一列为空；由主视图得，正方体排有2层，第2层右边为空；由左视图得，正方体第二层前边为空。
想象出的物体的形状如下图所示：例3、如图是某几何体的三视图，根据图中所标的数据求得该几何体的体积为（ ） A. 236π B. 136π C. 132π D. 120π分析：1、这是一个怎样的几何体？2、体积怎么算？ 解：这个几何体是由2个圆柱构成的，它的体积为：224822ππ⨯⨯+⨯⨯136π=交流 讨论 直接回答交流 讨论 直接回答逆向思考充分想象几何的形状与计算体积综合故选B。
高考在考查三视图方面出题有两个方向，一是给出三视图及相关数据，求几何体的体积、表面积、内切球体积或外接球体积等；二是给出几何体，确定其中一个视图的图形.由于第二点比较简单，所以高考中考查的较少.高考中对给出三视图求相关体积、面积等题型考查较多，一般以小题形式出现，分值为5分，该类型题的本质是考查三视图还原几何体，所以能快速准确的将三视图还原几何体，是解决这类问题的关键.王康民老师给大家介绍几种快速还原几何体的方法.先来复习一下三视图的相关知识：位置主在上，俯在下，左在右大小长对正，高平齐，宽相等虚实看的见的为实线，看不见的为虚线我来介绍两种快速又好用的三视图还原方法.当然，我默认大家已经掌握了基本几何体的三视图形状，这一点很重要，没有掌握的同学请麻利的自己去翻课本或者小册子.一．升点升线法1.升点法题目特征：当主视图和侧视图的顶部都是点时，采用升点法.如：还原如图所示的三视图的直观图.分析：观察三视图知主视图和侧视图的顶部都是点，则该图形可由俯视图的一个点升高形成，升的高度为主、侧视图的高2.用斜二测法画出俯视图，如下图所示：再根据其主视图为直角三角形，且直角在左侧，所以确定上升的点只能是点A，上升高度为2，三视图还原为下图所示.方法总结主、侧视图顶为点，上升点法1、俯视画图；2、主、侧找最高点；3、在俯视图上将找到的点上升（上升高度为主视图的高）2.升线法当主视图和侧视图的顶部为一点一线时，采用升线法.如：分析观察三视图知主视图和侧视图的顶部为一点一线，则该图形可由俯视图的一条线升高形成，升的高度为主、侧视图的高.用斜二测法画出俯视图，如下图所示.根据其主视图为正方形，左视图为直角三角形，且顶点在其左侧，所以确定上升的直线为线段AB，上升高度为主视图的高，如下图（左）所示.连接上顶点和下底面对应点，三视图还原为上图（右）所示.方法总结主、侧视图顶为一点一线，以点为基准升线.1、俯视画图；2、主、侧找升高线；3、升高直线（上升高度为主视图的高），连接对应点即可二．长方体中找点找面法我们所学的立体图形中，有锥、柱、台、球及组合体，像柱体和球的三视图还原就靠你自己了，简单到我都不想说.好，那就不说吧.我们通过研究锥体和台体的三视图还原来介绍这种方法.1.锥体的三视图还原锥体的三视图的特点是三个视图中有两个三角形.也就是说，我们在看到三视图的时候，如果其中有两个是三角形，我们能确定其为锥体.并且你要去还原它的主观图，这两个三角形就是关键！如：三视图如图所示.分析:首先三视图中有三个三角形，所以可以确定该几何体是一个椎体.俯视图就是该椎体的底面，大家要知道，一个椎体，如果底面确定了，再确定了顶点，则这个锥体就确定了.这个顶点是由主视图和侧视图的上顶点确定的，确定这个点是关键.第一步，我们取三个视图的长、宽、高分别为长、宽、高做出一个长方体，本题画出的正好是一个正方体，如图1所示.图1 图2 图3第二步：把主视图放到立方体正对着我们的这个面上，如图2所示.主视图的上顶点为图2中的顶点A，但该点不一定是锥体的顶点，由于主视图是由正前方看过去的，所以锥体的顶点应该在直线AA1上；再把侧视图放到立方体的右侧面上，如图3所示（注意侧视图是从左往右看的，不要画反了哦）侧视图的上顶点为图3中的顶点B，同理，锥体的顶点应该在直线AB上.所以直线AA1与直线AB的交点A即为锥体的顶点.第三步：将俯视图画在立方体中，由确定的底面和顶点，连接顶点与底面的各个顶点，锥体就确定了，如下图所示.直观图还原完成.步骤:1.三视图中有两个视图为三角形，确定该几何体为锥体，剩下的视图为该锥体的底面.2.将主视图和侧视图画在对应的立方体中，根据各自上顶点的投影线找其交点，确定锥体的顶点.3.俯视图作为底面，连接各顶点，锥体便还原出来了.方法:两个三角形→锥体.1、确定底面；2、确定顶点（主、侧视图上顶点的投影线交点）.3、各顶点连线.【变式训练】三视图如图所示，还原几何体的主观图.【提示】将侧视图作为锥体的底面，利用主视图和俯视图寻找顶点即可.【答案】如下图所示.2.台体的三视图还原台的特点是三视图中有两个梯形，剩下的视图作为台的下底面，还原时找上底面是关键。
