由视图到立体图形

《三视图》知识清单一、三视图的定义三视图是指能够正确反映物体长、宽、高尺寸的正投影工程图，分别是主视图、俯视图和左视图。

主视图是从物体的前面向后面投射所得的视图，能反映物体的前面形状；俯视图是从物体的上面向下面投射所得的视图，能反映物体的上面形状；左视图是从物体的左面向右面投射所得的视图，能反映物体的左面形状。

二、三视图的投影规律1、主视图和俯视图的长对正：也就是说，主视图和俯视图在水平方向上的长度是相等的。

2、主视图和左视图的高平齐：主视图和左视图在垂直方向上的高度是相等的。

3、俯视图和左视图的宽相等：俯视图和左视图在宽度方向上的尺寸是一致的。

这三个投影规律是绘制和阅读三视图的重要依据，必须牢记。

三、三视图的绘制步骤1、分析物体的结构形状：首先要仔细观察物体，了解其组成部分和各部分之间的相对位置关系。

2、确定主视图的方向：通常选择能最清晰地反映物体主要形状特征的方向作为主视图的投射方向。

3、绘制主视图：根据物体的实际尺寸和形状，按照投影规律画出主视图。

4、绘制俯视图：在主视图的下方，根据长对正的原则，画出俯视图。

5、绘制左视图：在主视图的右方，根据高平齐、宽相等的原则，画出左视图。

6、检查和修饰：完成三视图的绘制后，要仔细检查各视图之间的投影关系是否正确，尺寸是否标注完整，线条是否清晰等，并进行必要的修饰和整理。

四、三视图中的线条类型1、可见轮廓线：用粗实线绘制，表示物体的可见部分的轮廓。

2、不可见轮廓线：用虚线绘制，表示物体被遮挡的部分的轮廓。

3、中心线：用细点画线绘制，例如对称物体的对称中心线等。

五、由三视图还原立体图形这是三视图的一个重要应用，需要根据三视图所提供的信息，想象出物体的空间形状。

1、先从主视图入手，结合俯视图和左视图，确定物体的大致形状和结构。

2、分析各视图中线条的含义，特别是虚线所表示的不可见部分。

3、逐步构建物体的各个部分，注意它们之间的连接关系和相对位置。

六、三视图在实际生活中的应用1、机械制造：在设计和制造机械零件时，三视图是必不可少的工具，能够准确地表达零件的形状和尺寸，便于加工和装配。

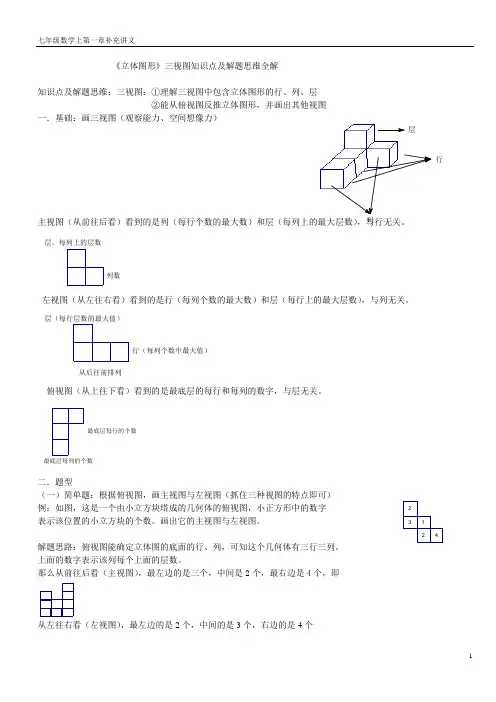
《立体图形》三视图知识点及解题思维全解知识点及解题思维：三视图：①理解三视图中包含立体图形的行、列、层②能从俯视图反推立体图形，并画出其他视图一．基础：画三视图（观察能力、空间想像力）主视图（从前往后看）看到的是列（每行个数的最大数）和层（每列上的最大层数），与行无关。

层，每列上的层数列数左视图（从左往右看）看到的是行（每列个数的最大数）和层（每行上的最大层数），与列无关。

从后往前排列层（每行层数的最大值）行（每列个数中最大值）俯视图（从上往下看）看到的是最底层的每行和每列的数字，与层无关。

最底层每行的个数最底层每列的个数二．题型（一）简单题：根据俯视图，画主视图与左视图（抓住三种视图的特点即可） 例：如图，这是一个由小立方块塔成的几何体的俯视图，小正方形中的数字 表示该位置的小立方块的个数。

画出它的主视图与左视图。

解题思路：俯视图能确定立体图的底面的行、列，可知这个几何体有三行三列。

上面的数字表示该列每个上面的层数。

那么从前往后看（主视图），最左边的是三个，中间是2个，最右边是4个，即从左往右看（左视图），最左边的是2个，中间的是3个，右边的是4个层行列24132（二）根据两种视图，判别立体图形的形状及组成数目。

1.中等题（空间想像力+逆向推理能力）：题目告诉俯视图。

解题思路：在俯视图上标上表示每个方块位置上的层数的数字。

例：下面是几何体的主视图和俯视图，请求出这个几何体最多要向个小立方体块？最少要几个小立方体块？俯视图主视图11131131133333最多块数最少块数解题思路：从俯视图开始分析，可以几何体最底层有三行三列；结合主视图看，第一列的层数最多是3层，第二列的层数最多是3层，最三列的层数最多是1层。

所以要想组成的小方块数最多，可以让每列中的任一层数都是最大值；要想组成的小方块数最少，必须让每一列层数中最多出现一个最大值，而其余每列上的层数都为1。

即：2.高难题（空间想像力+逆向推理能力+分类讨论）：题目未告诉俯视图 解题思路：先根据其它两种视图，画出俯视图，再标上表示层数的数字。

听课记录三视图
本节课的主要任务是引导学生完成由立体图形到视图，再由视图想到立体图形的复杂过程。

这对于刚刚接触几何的初一学生而言，无疑是一次较大的挑战，顺利地完成教学，对今后学习兴趣、信心的培养都是至关重要的，因此，我针对学生的心理特点及接受能力对教材做如下设计：首先我用苏轼的《题西林壁》巧妙地唤起学生的生活感受，让他们认识到视图的知识在生活中我们早有亲身体验，只是还没有形成概念，然后我再用“粉笔”这一简单的教具，让学生再次体会，加深认识，这样，教学与生活紧密相连，既有自然地导入课题，又消除学生对新知识的恐惧，同时还激发了学生浓厚的学习兴趣。

然后，我不适时地出示“三视图”这一概念，通过实验，让学生认识到视图就是由立体图形转化成的平面图形，并不断地训练、讨论、总结，得出画三视图的正确方法。

这时教师要巧妙点拨，学生如何从正面、上面、侧面三个角度来观察，既体现了学生的主体地位，又突出了教师的主导作用，锻炼了学生的动手操能力。

由视图到立体图形与上面的过程恰恰相反，需要学生根据视图进行想象，在大脑中构建一个立体形象。

我引导学生利用直观形象与生活中的实物进行联系，通过归纳、总结、对比的方法，有效的突破这一难点。

为了进一步地激发学生的学习兴趣，培养学生的想象能力和思维能力，可以让学生用一些小立方体随意摆出几种组合并描绘出它的视图，再由视图到立体图形的课堂训练。

最后，让学生归纳所学知识，进一步锻炼学生的概括能力，使知识系统化。

以上设计如有不妥之处，望老师们不吝赐教，我不胜感激。

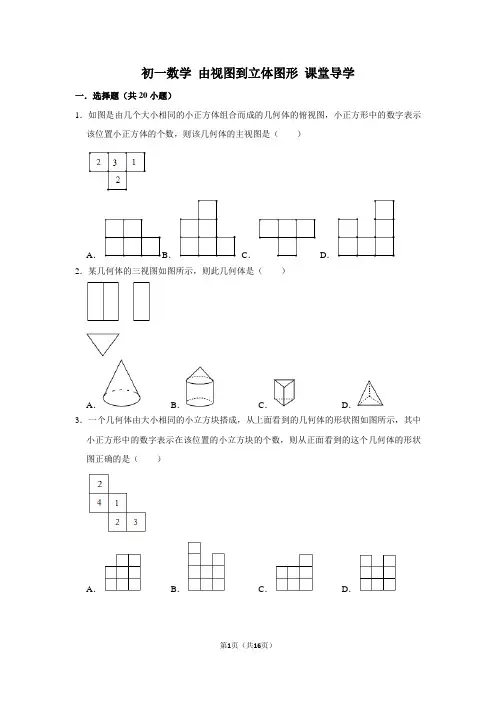
初一数学由视图到立体图形课堂导学一．选择题（共20小题）1．如图是由几个大小相同的小正方体组合而成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，则该几何体的主视图是（）A．B．C．D．2．某几何体的三视图如图所示，则此几何体是（）A．B．C．D．3．一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到的这个几何体的形状图正确的是（）A．B．C．D．4．某几何体的三视图如图所示，这个几何体是（）A．三棱柱B．球体C．圆锥体D．圆柱体5．如图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该方块的个数，则这个几何体的左视图为（）A．B．C．D．6．一个几何体的三视图如图所示，该几何体是（）A．正方体B．圆锥C．三棱柱D．四棱柱7．如图三视图所对应的直观图是下面的（）A．B．C．D．8．某几何体由一些大小相同的小正方体组成，如图是它的俯视图和主视图，那么组成该几何体的小正方体的个数最少为（）A．4个B．5个C．6个D．7个9．如图所示是由几个小立方块搭成的几何体的俯视图，则这个几何体左视图是（）A．B．C．D．10．如图是由5个立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方块的个数，则这个几何体的左视图是（）A．B．C．D．11．一个几何体由若干个相同的正方体组成，其主视图和左视图如图所示，则这个几何体中正方体最多有（）个．A．3B．4C．5D．612．若图是由几个相同的小正方体搭成的几何体的主视图和俯视图，则搭成这个几何体的小正方体的个数最少是（）A．6B．8C．10D．1213．从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图，那么构成这个几何体的小正方体有（）A．4个B．5个C．6个D．7个14．由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示，则搭成该几何体的小正方体的个数最多为（）A．7个B．8个C．9个D．10个15．某几何体的三视图如图所示，则此几何体是（）A．圆锥B．长方体C．圆柱D．四棱柱16．如图，是一个由多个相同小正方体搭成的几何体的俯视图，图中所标的数字为该位置小正方体的个数，则这个几何体的左视图是（）A．B．C．D．17．由几个大小相同的小正方体搭建而成的几何体的主视图和俯视图如图所示，则搭建这个几何体所需要的小正方体的个数至少为（）A．5B．6C．7D．818．如图是由6个立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方块的个数，则这个几何体的主视图是（）A．B．C．D．19．一个几何体由大小相同的小立方块搭成，它的俯视图如图所示，其中小正方形中的数字表示在该位置小立方块的个数，则该几何体的左视图为（）A．B．C．D．20．一个由若干个相同的小正方体组成的几何体的主视图和俯视图如图所示，则小正方体的最少个数为（）A．5个B．6个C．7个D．8个二．填空题（共30小题）21．由若干个小正方体组成的几何体的三视图如图所示，则组成这个几何体的小正方体的个数为．22．小颖同学到学校领来n盒粉笔，整齐地摞在讲桌上，从三面看到的平面图形如图所示，则n的值是．23．一个几何体由若干大小相同的小立方块搭成，如图分别是从它的正面、上面看到的形状图，那么搭成该几何体至少需用小立方块个．24．如图，是由几个边长为1的小立方体所组成的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数，则这个几何体的表面积为．25．由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示，则搭成该几何体的小正方体的个数最少是．26．若一个几何体由若干个完全相同的小正方体构成，并且该几何体从正面和上面看到的形状图如图所示．则构成这个几何体的小正方体的个数最少是．27．如图是由一些相同的小正方体构成的立体图形的三种视图，则构成这个立体图形的小正方体的个数是个．28．已知：如图是由若干个大小相同的小正方体所搭成的几何体从正面、左面和上面看到的形状图，则搭成这个几何体的小正方体的个数是．29．一个几何体由几个大小相同的小立方块搭成，从正面和上面看到的这个几何体的形状图如图所示，则该几何体最少是用个小立方块搭成的．30．如图是由几个相同的小正方体分别从上面、左面看到的形状图，这样的几何体最多需要个小立方体块，最少需要个小立方体块．31．用小立方块搭一个几何体，使得它从正面看和从上面看到的形状图如图所示，它最少要m个小立方块，最多要n个小立方块，则m+n的值为．32．用小立方体搭一个几何体，从它的正面、上面看到的形状图如图所示，则搭这样的几何体最多需要个小立方体，最少需要个小立方体．33．如图所示，是由一些相同的小立方体搭成的几何体分别从正面、左面、上面看到的该几何体的形状图，那么构成这个立体图形的小正方形有个．34．一个几何体由若干个相同的正方体组成，其主视图和俯视图如图所示，则这个几何体中正方体的个数最多是．35．如图所示是若干个大小相同的小正方体搭成的几何体从三个不同方向看到的图形，则搭成这个几何体的小正方体的个数是．36．一个几何体从正面和上面看到的图形如图所示，若这个几何体最多有a个小正方体组成，最少有b个小正方体组成，则a+b＝．37．用小立方块搭一几何体，它的主视图和俯视图如图所示，这个几何体最少要个立方块，最多要个立方块．38．一个几何体是由一些大小相同的小正方块摆成的，从正面看与从上面看得到的形状图如图所示，则组成这个几何体的小正方体的个数n的所有可能值的和是．39．用小立方体搭一个几何体，分别从它的正面、上面看到的形状如图所示．这样的几何体最少需要个小立方体；最多需要个小立方体．40．在桌子上摆有一些大小相同的正方体木块组成一个几何体，如图分别是从正面和从上面看到的形状图，组成这个几何体的小立方块个数最多需要块．41．一个几何体由多个完全相同的小正方体组成，它的三视图如图所示，那么组成这个几何体的小正方体的个数为个．42．由一些完全相同的小正方体搭成的几何体，分别从它正面和左面看到的几何体的形状图如图所示，组成这个几何体的小正方体的个数最少是，最多是．43．用小立方块指一个几何体，使它的从正面和从上面看到的这个几何体的形状图如图所示，这个几何体最少要a个小立方块，最多要b个小立方块，则a+b＝．44．由若干个相同的小正方形达搭成一个几何体，分别从正面和左面看，所得的形状如图所示，则搭建这个几何体所需的小正方体的个数最少是．45．一个几何体由若干大小相同的小立方块搭成，如图分别是从它的正面、上面看到的形状图，若该几何体所用小立方块的个数为n，则n的最大值和最小值之和为．46．一个几何体由若干大小相同的小立方块搭成的，如图分别是从它的左面，上面看到的平面图形，则组成这个几何体的小立方块最多有个．47．由若干个相同的小正方体搭成的一个几何体从正面和从左面看到的形状用如图所示，则所需的小正方体的个数最多是个．48．由一些大小相同的小正方体搭成的几何体从正面和从左面看到的图形如图，则搭成这个几何体的小正方体的个数最多为，最少为．49．用若干个相同的小正方体搭一个几何体，该几何体的主视图、俯视图如图所示．若小正方体的棱长为1，则搭成的几何体的表面积是．50．由几个小正方体组成的几何组合体的主视图、左视图如图所示，那么这几何组合体至少由个小正方体组成．三．解答题（共10小题）51．用若干个完全相同的小正方体搭成一个几何体，当从正面、上面看这个几何体时，得到的图形如图所示．问：在这个几何体中，小正方体的个数最多是多少？最少是多少？52．用小立方块搭成一个几何体，使它从正面和上面看到的形状图如图所示．搭建这样的几何体，最多要几个小立方块？最少要几个小立方块？53．一个几何体从正面和从上面看到的图形如图所示，若这个几何体最多有a个小正方体组成，最少有b个小正方体组成，求a+b的值．54．根据如图所给出的几何体从三个方向看得到的形状图，试确定几何体中小正方体的数目的范围．55．一个几何体由几块相同的小正方体叠成，它的三视图如下图所示．请回答下列问题：（1）填空：①该物体有层高；②该物体由个小正方体搭成；（2）该物体的最高部分位于俯视图的什么地方？（注：在俯视图上标注，并有相应的文字说明）56．一个物体是由棱长为3cm的正方体模型堆砌而成的，其视图如图：（1）请在俯视图上标出小正方体的个数（2）求出该物体的体积是多少．（3）该物体的表面积是多少？57．一个几何体是由若干个棱长为3cm的小正方体搭成的，从正面、左面、上面看到的几何体的形状图如图所示：（1）在“从上面看”的图中标出各个位置上小正方体的个数；（2）求该几何体的体积．58．用小正方体搭一个几何体，使它的主视图和俯视图如图所示，这样的几何体需要小正方体最多几块？最少几块？答：最多块；最少块．59．一个立体图形是由若干个小正方体堆积而成的，其三视图如图，则组成这个立体图形的小正方体有多少个．60．下面的图形是一个物体的三视图，请画出这个物体的形状．。