()两因素方差分析

双因素方差的定义和使用条件
双因素方差分析（Two-way ANOVA）是一种统计方法，用于分析两个因
素对实验结果的影响。

该方法主要用来检验两个因子对因变量的交互作用。

双因素方差分析特别适用于那些同时受到两个或更多因素影响的因变量研究。

使用双因素方差分析时，需要满足以下条件：
1. 独立性：各个观测值之间必须相互独立，这意味着每个观测值都不受其他观测值的干扰。

2. 正态性：样本必须来自正态分布总体。

3. 方差齐性：各个总体的方差必须相等，即抽样的总体必须是等方差的。

4. 样本容量：每个组中的观测值数量应该足够多，这样才能保证估计的参数接近真实值。

5. 满足其他假设：例如，误差项应该是随机的，并且服从均值为0的正态分布。

双因素方差分析的步骤如下：
1. 提出假设：包括主效应和交互效应的假设。

2. 方差分析表：列出观测值的数量、各组的均值和方差以及总均值和总方差。

3. F检验：通过F检验来检验主效应和交互效应的显著性。

4. 结果解释：如果F检验的结果显著，则说明主效应或交互效应对因变量有影响；否则，说明没有影响。

以上信息仅供参考，如需获取更多详细信息，建议咨询统计学专家或查阅统计学相关书籍。

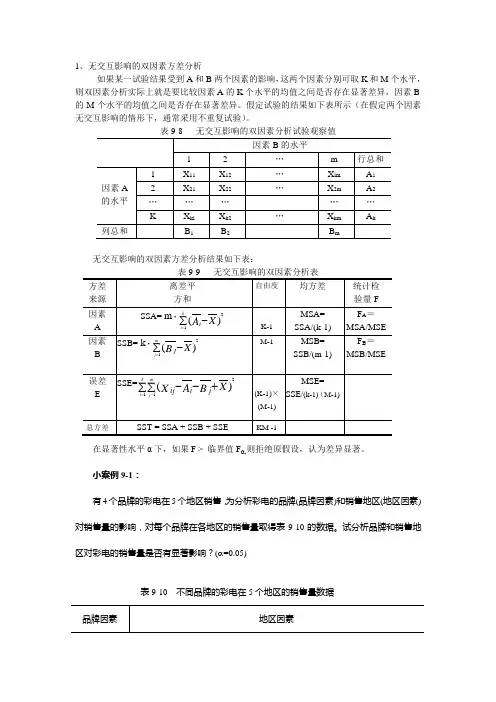
1、无交互影响的双因素方差分析如果某一试验结果受到A和B两个因素的影响，这两个因素分别可取K和M个水平，则双因素分析实际上就是要比较因素A的K个水平的均值之间是否存在显著差异，因素B 的M个水平的均值之间是否存在显著差异。

假定试验的结果如下表所示（在假定两个因素无交互影响的情形下，通常采用不重复试验）。

表9-8 无交互影响的双因素分析试验观察值无交互影响的双因素方差分析结果如下表：表9-9 无交互影响的双因素分析表在显著性水平α下，如果F > 临界值Fα,则拒绝原假设，认为差异显著。

小案例9-1：有4个品牌的彩电在5个地区销售，为分析彩电的品牌(品牌因素)和销售地区(地区因素)对销售量的影响，对每个品牌在各地区的销售量取得表9-10的数据。

试分析品牌和销售地区对彩电的销售量是否有显著影响？(α=0.05)表9-10 不同品牌的彩电在5个地区的销售量数据提出假设：对品牌因素提出的假设为：H0：m1=m2=m3=m4 (品牌对销售量无显著影响)H1：mi (i =1,2, …, 4) 不全相等(有显著影响)对地区因素提出的假设为：H0：m1=m2=m3=m4=m5 (地区对销售量无显著影响)H1：mj (j =1,2,…,5) 不全相等(有显著影响)表9-11 方差分析表结论：F品牌＝18.10777>Fα＝3.4903，拒绝原假设H0，说明彩电的品牌对销售量有显著影响。

F地区＝2.100846<Fα＝3.2592，不拒绝原假设H0，无证据表明销售地区对彩电的销售量有显著影响。

资料来源：贾俊平、何晓群、金勇进，《统计学》[M].北京: 中国人民大学出版社,2004.10第2版。

双因素方差分析结果解读双因素方差分析（Two-wayANOVA）是一种分析数据的统计方法，它可以检验同一总体的两个或多个变量之间的差异。

双因素方差分析的一个重要特点是它可以检验基于不同组别、不同资源或者不同情况下同一个总体上的差异。

它可以检验在多个组别之间存在差异、或者在不同组别之间存在偏差的情况。

本文将通过介绍双因素方差分析的原理、分析方法、结果解读方法，帮助读者更好地解读双因素方差分析的结果。

首先，双因素方差分析的原理是涉及两个不同的自变量，即因变量和一个或多个自变量。

因变量是一个连续的响应变量，而自变量则分为定类的自变量和定序的自变量，根据不同的实验需求采用不同的变量。

例如，定类的自变量可以用于比较基于性别或不同药物治疗后被试者的反应，定序的自变量则可用于比较基于疗程的不同反应。

其次，双因素方差分析需要构建一个双因素的实验单元，即一个自变量和一个因变量的实验设计，它可以确定每个组别之间的比较，比如在不同性别和不同处方药物治疗下被试者的反应。

双因素方差分析可以检验两个或多个因变量是否相对独立，以及独立或不独立的因变量是否存在差异。

最后，双因素方差分析的结果解读是比较重要的一步，它可以有效地解释出双因素实验单元下的差异或偏差，帮助研究者更好地做出他们的决策。

通常，根据双因素方差分析的结果可以检测出两个或多个自变量的差异，以及基于性别、时间、处方药物治疗等不同情况下的被试者的反应等。

只有当双因素方差分析的F值超过某一显著性水平的时候（通常为0.05或0.01），双因素方差分析的结果才被认为是显著的，可以通过结果解释和决策。

综上所述，双因素方差分析是一种非常有用的统计方法，可以检验同一总体的两个或多个变量之间的差异。

其中双因素方差分析原理，分析方法，以及结果解读方法都非常重要，有助于我们在解决实际问题时更好地解读双因素方差分析的结果，识别出不同组别，或者在不同组别之间存在的差异，从而发现新的实验结果，增加研究的学术价值。

两因素重复方差测量结果解读重复方差分析（RFA）是统计学中常用的一种分析方法，用于研究两种或多种因素变量之间的相互作用效果。

近年来，重复方差分析的应用越来越广泛，已成为社会科学研究领域中最常用的分析方法之一。

本文将针对重复方差分析中两因素的情形，对重复方差分析的概念、意义以及其在社会科学研究中的应用进行深入分析，最终提供一种有效的解释方案。

一、重复方差分析概述重复方差分析（RFA）是一种统计学方法，用于研究两个因素或多个因素之间的相互作用效果，常用来检验一个因素对另一个因素的影响程度，或者多个因素是否同时影响一个结果。

重复方差分析的基本原理是，将可以解释总变差的部分拆解成各个自变量和共同变量，以便研究它们之间的关系。

重复方差分析关注的是总变差的分配，以及那些变差是由自变量引起而不是其他因素引起。

二、两因素重复方差分析原理两因素重复分析（RFA）是其中一种重复分析方法，被认为是社会科学研究中最常用的分析方法之一。

两因素重复方差分析是指将总变差分解成自变量和共同变量的影响，仅使用两个因素：一个主要因素和一个控制变量，来检验假设模型的差异。

两因素重复方差分析可以用来检验主要变量对被观察变量的影响，以及它们之间的交互作用效果是否具有显著性。

三、两因素重复方差分析在社会科学研究中的应用重复方差分析不仅可以检验参与者之间的因素和变量之间的关系，也可以检验因素和变量之间的交互作用是否对结果有重要影响。

由于重复方差分析方法具有完整性和便捷性，因此在社会科学研究中被广泛用于各种社会和心理学概念的研究，以进一步了解影响变量的影响力以及它们之间的关系。

四、解释重复方差分析的措施重复方差分析的解释依赖于该研究的实际意义和研究设计，以利用上述因素和变量之间的关系提供准确的解释。

重复方差分析的解释包括以下几个方面：（1）检验双方变量；（2）检验主要变量的影响；（3）验双方变量的交互作用；（4）使用多元分析确定变量的重要性。

双因素方差分析spss步骤双因素方差分析SPSS步骤导言：双因素方差分析是一种常用的统计分析方法，用于分析两个或两个以上因素对于研究对象的影响是否存在差异。

在实际研究中，我们通常使用SPSS软件来进行双因素方差分析的计算和结果呈现。

本文将介绍使用SPSS软件进行双因素方差分析的步骤和注意事项。

一、准备数据在进行双因素方差分析之前，我们首先需要准备好所需的数据。

数据应该是一个二维矩阵，其中行代表不同的观测对象，列代表不同的变量。

变量可以分为两个因素，分别是因素A和因素B。

确保数据的格式正确，并且每一列都应该有对应的变量名称。

二、导入数据到SPSS打开SPSS软件，选择“文件”-“打开”-“数据”，然后选择包含你准备好的数据的文件。

在打开数据之后，你将看到数据被加载到SPSS软件的数据编辑器中。

三、设置变量属性在SPSS软件的数据编辑器中，右键点击每个变量的列，然后选择“变量视图”。

在变量视图中，你可以设置每个变量的属性，包括变量的名称、标签、测量尺度等。

对于因素A和因素B，你可以将它们设为分类变量。

四、进行双因素方差分析在SPSS软件中，选择“分析”-“一般线性模型”-“单因素”。

在对话框中，将因变量添加到“因变量”框中，将因素A和因素B 添加到“因子”框中。

确保选择双因素方差分析选项，并点击“确定”按钮。

五、检查假设条件在进行双因素方差分析之前，我们需要确保满足一些假设条件。

首先，各个观测值是彼此独立的，且满足正态分布假设。

其次，各个因子水平的方差相等。

可以使用一些统计方法，如Shapiro-Wilk 检验和Levene检验，来验证这些假设条件。

六、解读结果SPSS软件将为我们提供双因素方差分析的结果。

主要包括因素A 和因素B的主效应、交互效应以及误差项。

对于主效应，我们可以通过检查P值来决定该因素是否对因变量有显著影响。

对于交互效应，我们可以通过检查因素A和因素B的交互作用项的P值来判断是否存在显著交互效应。

第三节随机区组设计的两因素方差分析（two-way ANOVA）1、用途：用于随机区组设计的多个样本均数比较，其统计推断是推断各样本所代表的各总体均数是否相等。

随机区组设计考虑了个体差异的影响，可分析处理因素和个体差异对实验效应的影响，所以又称两因素实验设计，比完全随机设计的检验效率高。

该设计是将受试对象先按配比条件配成配伍组（如动物实验时，可按同窝别、同性别、体重相近进行配伍），每个配伍组有三个或三个以上受试对象，再按随机化原则分别将各配伍组中的受试对象分配到各个处理组。

值得注意的是，同一受试对象不同时间（或部位）重复多次测量所得到的资料称为重复测量数据（repeated measurement data），对该类资料不能应用随机区组设计的两因素方差分析进行处理，需用重复测量数据的方差分析。

2、计算公式：随机区组设计的两因素方差分析是把总变异中的离均差平方和SS 与自由度分别分解成处理间、区组间和误差三部分，其计算公式见表5.4。

表5.4两因素方差分析的计算公式变异来源离均差平方和自由度均方总N-1处理间k-1区组间b-1误差* # b区组数3、分析步骤（以例说明）：例5.2某医师研究A、B和C三种药物治疗肝炎的效果，将32只大白鼠感染肝炎后，按性别相同、体重接近的条件配成8个配伍组，然后将各配伍组中4只大白鼠随机分配到各组：对照组不给药物，其余三组分别给予A、B和C药物治疗。

一定时间后，测定大白鼠血清谷丙转氨酶浓度（IU/L），如表5.5。

问四组大白鼠的血清谷丙转氨酶是否相同。

表5.5 四组大白鼠血清谷丙转氨酶浓度（IU/L）区组对照组试验组合计A药组B药组C药组1 845.1 652.4 624.3 445.1 2566.92 834.7 741.3 772.3 432.5 2780.83 826.5 675.6 632.5 362.7 2497.34 812.8 582.8 473.6 348.7 2217.95 782.8 491.8 462.8 345.9 2083.36 745.6 412.2 431.8 312.8 1902.47 730.4 494.6 484.9 296.3 2006.28 684.3 379.5 380.7 228.4 1672.96262.2 4430.2 4262.9 2772.4 17727.7 ()782.78 553.78 532.86 346.55 553.99()4925110.04 2571668.14 2391246.57 995764.14 10883788.89 ()本研究的主要目的在于比较不同治疗方法的效果，同时还可以比较不同区组间大鼠血清谷丙转氨酶浓度是否相同。

专题研究 ZHUANT IYANJ I U92　数学学习与研究　201017单因素及双因素方差分析及检验的原理及统计应用◎张　玲　(辽宁丹东地质工程职业学院　118008)　 【摘要】本文主要介绍了方差分析的基本原理及其统计应用,并总结出进行方差分析的计算步骤、计算公式汇总、离差的分解,同时利用单因素及双因素的方差分析的原理对生产中的实际问题做了比较详实的剖析,以便对学生在学习这一理论的过程中能深入浅出,加深理解.【关键词】单因素方差分析;双因素方差分析;离差分解;F 检验方差分析是研究一个(或多个)自变量对一个(或多个)因变量影响的方法.在科学试验和生产实践中,影响一事物的因素往往是很多的.例如,在化工生产中,在原料成分、原料剂量、催化剂、反应温度、压力、溶液浓度、反应时间、机器设备操作人员的水平等因素,每一因素的改变都有可能影响产品的数量和质量,有些因素影响较大,有些较小,为了使生产过程得以稳定,保证优质、高产,就有必要找出对产品质量有显著影响的那些因素.为此,我们需要进行试验.方差分析就是根据试验结果进行分析,鉴别各个有关因素对试验结果的影响的有效方法.我们称自变量为因素,单个表现形式为因素分组.可根据因素个数划分方差分析的类型.若只有1个自变量和1个因变量,则称为单因素方差分析;相应的,若有2个自变量,则称为双因素方差分析,以此类推.若因变量多于一个,则称为多维方差分析.进行方差分析的过程我将其总结为三个步骤:(1)表述问题.(2)分析离差平方和.(3)检验统计独立性.一、单因素方差分析11表述问题为了找出方差分析的核心,我们先看下面这个问题:为了考察某种化工产品收率(%)的影响,选择了四种不同的温度.在同一温度下,各做五次试验.测得的结果如下表所示:表1:试验结果表 试验号温　度 12345平均收率60℃84908793818765℃97899688959370℃92878287828675℃817989908184 总平均收率x =8715.我们的目的是考察温度这个因素对产品收率的影响,所以在做试验时,除了温度外,其他条件如工人的技术水平、原材料、试验器械等都要尽可能地相同.从平均收率来看,好像温度对收率有一定的影响.但仔细观察一下又不是那样直观.表现在:(1)同一温度下的收率并不完全一样.所以产生这种差异,是由于试验过程中存在着各种偶然因素的干扰和测量误差等因素所致.这一类误差统称为试验误差或随机误差.(2)存在着不同温度的影响.这种由于条件变更引起的差异,称为条件变差.现在的问题为:试验误差和条件变差哪一个是主要的.如果条件变差是主要的,那么应选择较好的工艺条件进行生产或确定进一步的试验方向.为了叙述方便,我们把不同条件称为水平,上面的例子中,温度分为四个水平,机器分为m 个水平.这里我们引入如下记号:x ij =观察值.其中:i:作为自变量表现形式的因素分组标号(i =1,2,3,…);j :因素分组内观察值的标号(j =1,2,3,…);x i :因素分组观察值的平均值;x:所有观察值的总均值.21分析离差平方和我们可以这样理解,若温度对收率无影响,则某化工产品收率的预测值是x .若假设温度对收率有影响,则应根据温度,化工产品的预测值分别为x 1,x 2,x 3,x 4.观察值与预测值的偏差(x ij -x i )归因于随机外部影响,因而未被解释.于是,总离差可分解为两部分(所谓的离差分解):总离差=已解释离差+未解释离差.在方差分析中,可将上述单个观察值的总离差分解推广到所有观察的离差平方和.即总离差平方和=因素分组间离差平方和+因素分组内离差平方和.现将方差分析计算公式总结如下表二所示:表2:一个因素的方差分析表偏差来源偏差平方和自由度均　方组　间Q 1=n∑ni =1(x i -x )2m -1S 21=Q 1m -1组　内Q 2=∑mi =1∑nj =1(x ij -x i )2m n -mS 22=Q 2m n -m 总　和Q =∑mi =1∑nj =1(x ij -x )2m n -1S 2=Q 2m n -1 ZHUANT IYANJ I U 专题研究93数学学习与研究　201017 我们把数据按表二计算如下:表3:离差平方的计算偏差来源偏差平方和自由度均　方组　间Q1=n∑ni=1(xi-x)2=195m-1=3S21=Q1m-1=65组　内Q2=∑mi=1∑nj=1(xij-x i)2=334m n-m=16S22=Q2m n-m=201875总　和Q=∑mi=1∑nj=1(xij-x)2=546m n-1=191S2=Q2m n-1=281737 31检验统计独立性我们认为求出的因素分组间和因素分组内方差表明,可猜测因子“温度”对产品的收率没有影响,为了能在统计上检验此猜测,我们用S21比S22:F实际=S21S22,其中F实际表示实际F值.根据表四有F实际=S21S22=65201875=311138.实际F值的评价标准取决于F分布的状况.检验的出发点是零假设(H):不同的温度对产品收率相同;备选假设H1为:不同的温度对产品的收率的影响不同.F检验提出的问题用公式表示为:H0:α1=α2=α3=0.H1:至少有一个α值≠0.通过比较F值与查表所得的理论F值进行检验,理论F值表对各信任概率给出的一个检验值,如果给定的显著水平为α=0105,则F0105(3116)=3124,由于311138<3124,所以认为温度对产品的收率没有显著影响.二、双因素方差分析我们上面讨论的是单因素的方差分析,但是影响产品质量和数量的重要因素往往不只一个,例如,机器、工人的技术水平、原料等都是重要因素.这就需要讨论多因素的方差分析.为了方便起见,我们对于两个因素的方差分析也可以总结成下表所示的形式,便于同学们计算及记忆和理解.表4:两个因素的方差分析表偏差来源平方和自由度均　方F值A的影响Q1=n∑ni=1(xi-x)2m-1S21F A=S21S23B的影响Q2=m∑nj=1(xj-x)2n-1S22F B=S22S23交互影响A×BQ3=c∑mi=1∑nj=1(xij-x i-x j+x)2(m-1)·(n-1)S23=Q3(n-1)(m-1)F A×B=S23S24误差Q4=∑mi=1∑nj=1(xij-x i-x j+x)2m n(c-1)S24=Q4m n(c-1)总和Q=∑mi=1∑nj=1(xij-x)2m nc-1 那么我们还是按照上面所论述的因素方差分析的步骤进行两个因素的方差分析.11表述问题要试验8台同类机器性能是否相同,4名工人的技术是否有显著差异,使每位工人在每台机器上操作一个工作日得到产量如表五所示:表5:某种橡胶各种不同配方试样的拉力 氧化锌(B)拉伸力 促进剂(A) 一二三四131.3334.3635.3639.38233.3436.3737.3938.41335.3737.3839.4042.44 21分析离差平方和根据方差分析基本原理(离差分解)我们以如下树形图为基础.根据上图有如下关系式:总偏差=因素A造成的偏差+因素B造成的偏差+因素A和B的交互作用造成的偏差+组内偏差.将其结果计算如下表六所示:表6:某种橡胶不同配方拉伸力的方差分析表偏差来源平方和自由度均　方F　值A56.6228.319.4B132.2344.130.2A×B4.760.80.55误　差17.5121.46总　和211.023 31检验统计独立性在双因素方差分析中,比较所有的均值可以检验两个因素的不同效应.若所有的均值相等,则可假设两个因素的各因素分组对因变量的影响相同(零假设).否则,可假设至少一个因素分组与其他因素分组产生的影响不同(备选假设).其他问题的解决涉及各因素及交互效应的单独分析.此时的零假设为:各因素分组及交互效应的平均值相等.根据计算的方差分析表,对α=0101,F0101(2112)=619,F0101(2112)=6,F0101(0112)=4182,因1914>619,3012>6,0155<4182,所以促进剂和氧化锌的影响都是显著的,而它们的交互作用则可以忽略.三、方差分析的推广在以上的论述中,我们都认为每个单元格中的观察值个数相同,方差分析的第一个推广是引入数据个数不等的单元格,由此须调整标准差分解分式,但标准差分解的原理不变,只是增加对每个观察值的加权.另一个推广是在分析引入两个以上的因素,标准差分解的原理同样保持不变.例如,三因素方差分析与双因素方专题研究 ZHUANT IYANJ I U 94　数学学习与研究　201017差分析的原理相同,加入第三个因素仅使标准差分解略微发生变化.总离差平方和分解如下图所示:三因素设计的总离差平方和分解与双因素方差分析相比,三因素方差分析的特点在于,可能的交互效应有两个层面:一是因素间两两的交互效应,二是所有的三个因素的交互效应.分析中引入三个以上的因素,则因素交互效应的分析层面相应增多,但此时交互作用的实际意义就会降低或减少.若根据F 检验,拒绝所有的因素分组影响相同的零假设,则必然会产生这样的问题:哪些因素分组的影响不同于其他?对此,可运用所谓的我维检验(均值检验).该检验实现了成对均值的比较或均值线性组合间的比较.四、方差分析的应用建议要应用方差分析,必须满足一些前提条件,这涉及调查数据特征和数据的评价.从科学理论角度看,必须提出关于自变量(如温度)与因变量(如收率)间影响关系的假设,要由方差分析解答的理论问题不能先从数据中得出.除了得出统计上显著的结果,还能否得出具有重要实际意义的论断取决于影响关系假设的质量.统计方法对数据的选择提出了一定要求.在研究中,自变量可能具有任意的测试标准(名义、序数及基数的尺度),但因变量必须是基数测度的.因素间必须具有明显的区别,就是说,它们的必须是完全不同的因变量影响量.若从两个假定不同因素中得出相同的关系,则因变量的波动不再明确地归因于其中一个因素.【参考文献】[1]盛骤.概率与数理统计.北京:高等教育出版社,2001(12).[2]李志伟.统计分析概论.北京:对外贸易出版社,1984(10).[3][德]克劳斯·巴克毫斯.多元统计分析方法.上海:上海人民出版社,2008(10).[4][美]P .L.Meyer .概率引论及统计应用.北京:高等教育出版社,1986(8).[5]薛毅.最优化原理和方法.北京:北京工业大学出版社,2001(1).[6]孙文瑜,徐成贤,朱德通.最优化方法[M ].北京:高等教育出版社,2004(1).[7]吴乙申.应用统计学.北京:机械工业出版社,1986(11).(上接91页)52z 5x 5y=-sec 2x sec 2y tan (x +y )-　sec 2x tan y sec 2(x +y )-tan x sec 2y sec 2(x +y ),µ∼52z 5y2=-2tan x sec 2y sec 2(x +y )-2tan x tan y tan (x +y )[sec 2y +sec 2(x +y )].νυ联立组成方程组5z 5x=-sec 2x tan y tan (x +y )-tan x tan y sec 2(x +y )=0,5z 5y=-tan x sec 2y tan (x +y )-tan x tan y sec 2(x +y )=0,解之得x =π3,y =π3.∴x =y =p =π3.将x =y =p =π3分别代入 µ} µ∼ νυ,得A =123,B =83,C =123,Δ=B 2-AC =(83)2-123·123=-240<0,且A =123>0,∴由命题1知:z =tan x tan y tan p 在x =y =p =π3时取得极小值,极小值为z 极小=tanπ3tan π3tan π3=33.由这个问题的实际意义知该极小值就是所求最小值.解法2(利用拉格朗日乘数法)　略.推广6　在三角形ABC 中,x,y,p 分别是它的三个内角,求tanx m tan y m tanpm(m 是不小于1的实数)的最值.总之,有了导数这一有力的武器,三角形中同名三角函数的最值就转化成了简单的求导运算,有了这种普遍适应的方法,学生也就不再需要刻意的去记一些特殊的技巧和方法,就能方便、快捷地求出最值.但是使用导数方法一定要检验问题是否只有满足命题1或命题2的条件,在满足命题1或命题2的条件下,才能应用该方法.【参考文献】[1]曾庆柏.大学数学应用基础(下).长沙:湖南教育出版社,2004:70.[2]同济大学数学系.高等数学(下).北京:高等教育出版社,2007:115.。