当前位置：文档之家 › 双因素和多因素方差分析

双因素和多因素方差分析

  • 格式：ppt
  • 大小：950.50 KB
  • 文档页数：57

下载文档原格式

  / 57

合集下载

方差分析(包括三因素)讲解

方差分析(包括三因素)讲解

2、CLASS 变量表；
CLASS必须的MODEL之前。
3、MODEL 因变量表=效应；
输出因变量均数，对主效应均数间的检
4、MEANS 效应[/选择项]；
验。
5、ALPHA=p 显著性水平（缺省值为0.05）
是指因变量与自变量效应，模型如下：
1、主效应模型 MODEL y=a b c; (a b c是主效应，y是因变量）
计判断，得出结论。
5
方差分析的基本思想：把全部数据关于总均值的离差平方和 分解成几部分，每一部分表示某因素诸水平交互作用所产生 的效应，将各部分均方与误差均方相比较，从而确认或否认 某些因素或交互作用的重要性。
用公式概括为：
各因素引起
由个体差异 引起（误差）
总变异=组间变异+组内变异
种类：常用方差分析法有以下4种 1、完全随机设计资料的方差分析（单因素方差分析） 2、随机区组设计资料的方差分析（二因素方差分析） 3、拉丁方设计资料的方差分析（三因素方差分析） 4、R*C析因设计资料的方差分析（有交互因素方差分析）
3
第一节 概述
因素（因子）—— 可以控制的试验条件 因素的水平 —— 因素所处的状态或等级 单（双）因素方差分析——讨论一个（两个） 因素对试验结果有没有显著影响。
4
例如：某厂对某种晴棉漂白工艺中酸液浓度（g/k）进 行试验，以观察酸液浓度对汗布冲击强力有无显著影 响。
冲击强力 序号
1
浓度
2 3 4 56
计算出F值：
QA
4217.3
(3 1) 2 28.38
QE
1114.7
(3(6 1))
5
15
列表：
方差来源 因素A 试验误差 总误差

方差分析2（双因素方差分析、多元方差分析、可视化）

方差分析2（双因素方差分析、多元方差分析、可视化）

⽅差分析2（双因素⽅差分析、多元⽅差分析、可视化）1 双因素⽅差分析1.1 双因素⽅差分析的实战dat<-ToothGrowthdatattach(dat)table(dat$supp,dat$dose)aggregate(len,by=list(dat$supp,dat$dose),FUN=mean)解释：根据投⽅式（橙汁OJ，维C素VC）supp和剂量dose来对⽛齿的长度len进⾏求均值dose<-factor(dose)解释：为了避免把dose变量认为是数值变量，⽽是把dose认为成分组变量，所以设置成因⼦类型factorfit<-aov(dat$len~dat$supp*dat$dose)解释：aov()做⽅差分析，把 + 换成了 * ，这两项dat$supp和dat$dosee就变成了交互项summary(fit)结果分析：可以看出P值很⼩，三个P值都⼩于0.05，说明不同的投喂⽅式supp对⽛齿的⽣长长度len是有显著影响的；说明不同的剂量dose对⽛齿的⽣长长度len是有显著影响的；说明在两种投喂⽅式下，不同的投喂⽅式supp和剂量dose的交互效应对⽛齿的⽣长长度len是有显著影响的1.2 可视化⽅法1interaction.plot(dat$dose,dat$supp,dat$len,type = "b",col=c("red","blue"),pch=c(16,18),main="XX")1.3 可视化⽅法2library(gplots)plotmeans(dat$len~interaction(dat$supp,dat$dose,sep=" "),connect=list(c(1,3,5),c(2,4,6)),col=c("red","blue"),main="XX",xlab="xlab")1.4 可视化⽅法3library(HH)interaction2wt(dat$len~dat$supp*dat$dose)2 重复测量⽅差分析dat<-CO2CO2$conc<-factor(CO2$conc)w1b1<-subset(CO2,Treatment=="chilled")uptake是植物光合作⽤对⼆氧化碳的吸收量，是因变量y，type是组间因⼦，是互斥的，表⽰的是两个不同地区的植物类型，要么是加拿⼤的植物，要么是美国的植物，不可能两个地⽅都是，conc是不同的⼆氧化碳的浓度，每⼀种植物都在所有的⼆氧化碳浓度下，所以conc是组内因⼦研究不同地区的植物作⽤，在某种⼆氧化碳的浓度作⽤下，对植物的光合作⽤效果有没有影响2.1 含有单个组内因⼦w和单个组间因⼦B的重复测量ANOVAfit<-aov(uptake~conc*Type+Error(Plant/(conc)),w1b1)summary(fit)结果分析：⼆氧化碳浓度和类型对植物光合作⽤都有显著影响2.2 可视化图形呈现（1）⽅式⼀par(las=2)par(mar=c(10,4,4,2))with(w1b1,interaction.plot(conc,Type,uptake,type = "b",col=c("red","blue"),pch=c(16,18)))（2）⽅式⼆boxplot(uptake~Type*conc,data=w1b1,col=c("red","blue"))3 多元⽅差分析library(MASS)attach(UScereal)dat<-UScerealshelf<-factor(shelf)y<-cbind(calories,fat,sugars)fit<-manova(y~shelf)summary(fit)结果分析：不同的货架shelf上，⾷物的热量calories，脂肪含量fat和含糖量sugars是⾮常显著不同的3.1 多元正态性center<-colMeans(y)n<-nrow(y) #⾏数p<-ncol(y) #列数cov<-cov(y) #计算⽅差d<-mahalanobis(y,center,cov)coord<-qqplot(qchisq(ppoints(n),df=p),d) #画图abline(a=0,b=1) #画参考线identify(coord$x,coord$y,labels = s(UScereal)) #给出交互式标出离群点3.2 稳健多元⽅差分析install.packages("rrcov")library(rrcov)wilks.test(y,shelf,method="mcd")结果分析：P值⼩于0.05，说明结果是显著性的，即不同货架上⾷物的热量calories，脂肪含量fat和含糖量sugars是⾮常显著不同的4 ⽤回归来做ANOVAlibrary(multcomp)dat<-cholesterollevels(dat$trt)fit.aov<-aov(response~trt,data=dat)summary(fit.aov)结果分析：aov⽅差分析，trt对response的影响⾮常显著fit.lm<-lm(response~trt,data=dat)summary(fit.lm)结果分析：lm回归分析，trt对response的影响⾮常显著，并且trt的每⼀项都显⽰出来了。

第九章双因素和多因素方差分析

第九章双因素和多因素方差分析

第九章双因素和多因素方差分析引言方差分析是一种常用的统计方法，用于比较两个或多个组之间的差异。

双因素和多因素方差分析是方差分析的扩展，允许考虑两个或多个自变量对因变量的影响。

本文将介绍双因素和多因素方差分析的概念、假设检验、模型构建等内容。

双因素方差分析双因素方差分析主要用于对两个自变量对因变量的影响进行分析。

其中一个自变量称为因子A，另一个自变量称为因子B。

通过双因素方差分析，我们可以了解到两个自变量对因变量的主效应以及交互效应。

假设检验进行双因素方差分析时，我们需要对两个自变量的主效应和交互效应进行假设检验。

主效应是指每个因子对因变量的影响，交互效应是指两个因子之间是否存在相互影响。

在进行双因素方差分析时，我们需要提出以下假设：•零假设H0: 两个因子对因变量没有主效应和交互效应•备择假设H1: 至少一个因子对因变量有主效应或交互效应然后，我们可以通过方差分析结果的显著性检验来判断是否拒绝零假设。

模型构建双因素方差分析可以通过构建线性模型来进行。

通常，我们使用以下模型进行双因素方差分析：Y = μ + α + β + (αβ) + ε其中，Y表示因变量，μ表示总体均值，α表示因子A的主效应，β表示因子B的主效应，(αβ)表示交互效应，ε表示误差。

通过对数据进行拟合并计算模型中的各个参数，我们可以得到双因素方差分析的结果。

多因素方差分析多因素方差分析是对多个自变量对因变量的影响进行分析。

多因素方差分析可以包含两个以上的自变量，并且可以考虑每个自变量的主效应和交互效应。

假设检验进行多因素方差分析时，我们同样需要对每个自变量的主效应和交互效应进行假设检验。

假设检验的步骤与双因素方差分析类似。

模型构建多因素方差分析的模型构建与双因素方差分析类似，但是需要考虑多个自变量的影响。

Y = μ + α1 + α2 + … + αn + β + (αβ) + ε其中，Y表示因变量，μ表示总体均值，α1, α2, …, αn表示各个自变量的主效应，β表示交互效应，(αβ)表示两个或多个自变量之间的交互效应，ε表示误差。

论文—双因素试验的方差分析

论文—双因素试验的方差分析

X ijk ~ N (ij , 2 ) （ ij 和 2 未 知 ）， 记 X ijk i = ijk ， 即 有
ijk X ij ijk ~ N (0, 2 ), 故 X ijk ijk 可视为随机误差. 从而得到如下数学模型
X ijk ij ijk， ijk ~ N（0， 2）， 各 ijk 相互独立， i 1, , r; j 1, , s; k 1, , t;
1 st
1 rt
X
j 1 k 1
r t
s
t
ijk
，i=1，2， ，r，
X
j =
X
i 1 k 1
类似地，引入记号： ， i , j , i , j , 易见

i 1
r
i 0 ，

j 1
s
j
0.
为水平 B j 的效应. 这样可以将
仍称 为总平均，称 i 为水平 A i 的效应，称 成
ij
j
ij
表示
= + i + j +
ij
（ i 1, , r; j 1, , s ） ，
(3)
与无重复试验的情况类似，此类问题的检验方法也是建立在偏差平方和的分解上的。 2. 偏差平方和及其分解 引入记号： X =
1 rst
X
i 1 j 1 k 1
r
s
t
ijk
，
X
ij =
1 X ijk ，i=1，2， ，r，j=1，2， ，s， t k 1

t
X
i =
试 验 结 因 素 果 A 因 素 B

方差分析与回归分析

方差分析与回归分析

方差分析与回归分析在统计学中，方差分析（ANOVA）和回归分析（Regression Analysis）都是常见的统计分析方法。

它们广泛应用于数据分析和实证研究中，有助于揭示变量之间的关系和影响。

本文将对方差分析和回归分析进行介绍和比较，让读者更好地理解它们的应用和区别。

一、方差分析方差分析是一种统计方法，用于比较两个或更多组别的均值是否存在显著差异。

它通过计算组内变异和组间变异的比值来判断不同组别间的差异是否具有统计显著性。

在方差分析中，通常有三种不同的情形：单因素方差分析、双因素方差分析和多因素方差分析。

单因素方差分析适用于只有一个自变量的情况。

例如，我们想要比较不同教育水平对收入的影响，可以将教育水平作为自变量分为高中、本科和研究生三个组别，然后进行方差分析来检验组别之间的收入差异是否显著。

双因素方差分析适用于有两个自变量的情况。

例如，我们想要比较不同教育水平和不同工作经验对收入的影响，可以将教育水平和工作经验作为自变量，进行方差分析来研究其对收入的影响程度和相互作用效应。

多因素方差分析适用于有多个自变量的情况。

例如，我们想要比较不同教育水平、工作经验和职位对收入的影响，可以将教育水平、工作经验和职位作为自变量，进行方差分析来探究它们对收入的联合影响。

方差分析的基本原理是计算组内变异和组间变异之间的比值，即F 值。

通过与临界F值比较，可以确定差异是否显著。

方差分析的结果通常会报告组间平均差异的显著性水平，以及可能存在的交互作用。

二、回归分析回归分析是一种统计方法，用于研究自变量与因变量之间的关系。

它通过建立一个数学模型来描述自变量对因变量的影响程度和方向。

回归分析分为简单线性回归和多元线性回归两种类型。

简单线性回归适用于只有一个自变量和一个因变量的情况。

例如，我们想要研究体重与身高之间的关系，可以将身高作为自变量、体重作为因变量，通过拟合一条直线来描述二者之间的关系。

多元线性回归适用于有多个自变量和一个因变量的情况。

统计学第九章 双因素和多因素方差分析

统计学第九章 双因素和多因素方差分析
2 （ y ijk − y ij•） ∑∑∑ i =1 j =1 k =1 a b n
2、平方和的分解
与平方和相应的自由度分别为： 总自由度：df =abn-1
T
A因素处理间自由度：df =a-1
A
B因素处理间自由度：df =b-1
B
交互作用自由度：df =(a-1)(b-1)
AB
处理内自由度：dfe=ab(n-1) df =df +df +df +dfe
a b i=1 j =1
n
2
SSe= ∑∑∑yijk
i=1 j =1 k =1
a
b
2
1 a b 2 − ∑∑yij• = SST − SSA − SSB − SSAB n i=1 j=1
（五）各项均方的计算
MS
T
SS T SS T = = df T abn − 1
MS
A
SS A SS A = = a -1 df A
x9
x1 x2 x3 x4 x5 x6 x7 x8 33.5** 30.5** 29.75** 22** 19** 11.5 2.75 2.5
x8
31** 28** 27.25** 19.5** 16.5** 9 0.25
x7
30.75** 27.75** 27** 19.25** 16.25** 8.75
A因素误差平方和
SSA = bn∑(yi•• − y••• )
i=1
a
2
B因素误差平方和 SSB = an∑(y• j• − y••• )
b j=1
2
AB交互作用误差平方和
SSAB = n∑∑(yij• − yi•• − y• j• + y••• )

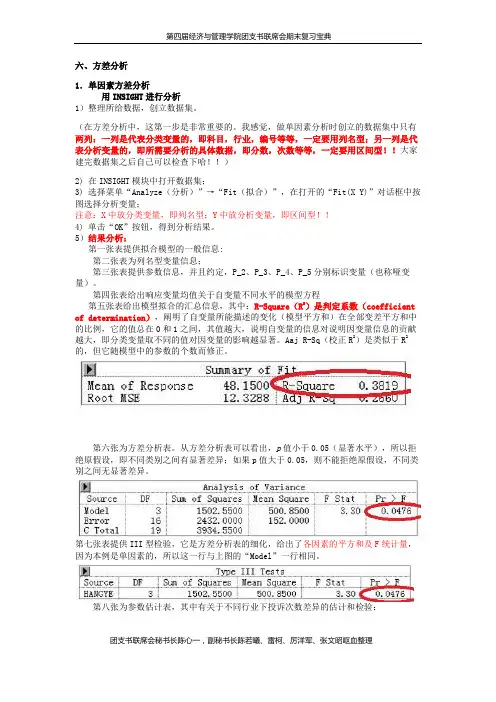
SAS整理下之方差分析

SAS整理下之方差分析

六、方差分析1．单因素方差分析用INSIGHT进行分析1）整理所给数据，创立数据集。

（在方差分析中，这第一步是非常重要的。

我感觉，做单因素分析时创立的数据集中只有两列：一列是代表分类变量的，即科目，行业，编号等等，一定要用列名型；另一列是代表分析变量的，即所需要分析的具体数据，即分数，次数等等，一定要用区间型！！大家建完数据集之后自己可以检查下哈！！）2) 在INSIGHT模块中打开数据集；3) 选择菜单“Analyze（分析）”→“Fit（拟合）”，在打开的“Fit(X Y)”对话框中按图选择分析变量；注意：X中放分类变量，即列名型；Y中放分析变量，即区间型！！4) 单击“OK”按钮，得到分析结果。

5）结果分析：第一张表提供拟合模型的一般信息:第二张表为列名型变量信息；第三张表提供参数信息，并且约定，P_2、P_3、P_4、P_5分别标识变量（也称哑变量）。

第四张表给出响应变量均值关于自变量不同水平的模型方程第五张表给出模型拟合的汇总信息，其中：R-Square（R2）是判定系数（coefficient of determination），阐明了自变量所能描述的变化（模型平方和）在全部变差平方和中的比例，它的值总在0和1之间，其值越大，说明自变量的信息对说明因变量信息的贡献越大，即分类变量取不同的值对因变量的影响越显著。

Aaj R-Sq（校正R2）是类似于R2的，但它随模型中的参数的个数而修正。

第六张为方差分析表。

从方差分析表可以看出，p值小于0.05（显著水平），所以拒绝原假设，即不同类别之间有显著差异；如果p值大于0.05，则不能拒绝原假设，不同类别之间无显著差异。

第七张表提供III型检验，它是方差分析表的细化，给出了各因素的平方和及F统计量，因为本例是单因素的，所以这一行与上图的“Model”一行相同。

第八张为参数估计表，其中有关于不同行业下投诉次数差异的估计和检验：1) 根据标识变量的定义，Intercept后的估计47.4是对应于旅游业投诉次数的均值，其后的t检验是检验这一均值是否为0。

方差分析的若干模型

方差分析的若干模型

方差分析的若干模型方差分析（Analysis of variance，简称ANOVA）是一种常用的统计方法，用于比较两个或多个样本的平均差异是否显著。

它的基本原理是将总体方差分解为组内方差和组间方差，然后通过比较组间方差与组内方差的大小以判断组间差异的显著性。

在实际应用中，根据具体情况可以选择多种不同的ANOVA模型进行分析。

一元方差分析模型：一元方差分析适用于只有一个自变量的情况，用于比较不同水平之间的平均差异是否显著。

该模型的方程可以表示为：Y=μ+αi+ε，其中Y为观测值，μ为总体均值，αi为第i个水平的效应，ε为误差项。

一元方差分析的前提是误差项满足独立同分布的正态分布假设。

双因素方差分析模型：双因素方差分析适用于有两个自变量的情况，用于比较两个自变量的不同水平和水平间的交互效应对因变量的影响是否显著。

该模型的方程可以表示为：Y = μ + αi + βj + (αβ)ij + ε，其中Y为观测值，μ为总体均值，αi和βj分别表示第i个和第j个自变量的水平效应，(αβ)ij表示自变量i和自变量j的交互效应，ε为误差项。

双因素方差分析的前提是误差项满足独立同分布的正态分布假设。

多因素方差分析模型：多因素方差分析适用于有多个自变量的情况，用于比较多个自变量的不同水平和水平间的交互效应对因变量的影响是否显著。

该模型的方程可以表示为：Y = μ + αi + βj + γk +(αβ)ij + (αγ)ik + (βγ)jk + (αβγ)ijk + ε，其中Y为观测值，μ为总体均值，αi、βj和γk分别表示第i个、第j个和第k个自变量的水平效应，(αβ)ij、(αγ)ik和(βγ)jk表示自变量i与自变量j、自变量i与自变量k以及自变量j与自变量k的交互效应，(αβγ)ijk表示三个自变量的交互效应，ε为误差项。

重复测量方差分析模型：重复测量方差分析适用于在同一组个体上进行多次测量的情况，用于比较不同时间点或处理条件对因变量的影响是否显著。

生物统计第8章两因素及多因素方差分析

生物统计第8章两因素及多因素方差分析
生物统计第8章两因素及多因素方 差分析
目录
• 引言 • 两因素方差分析 • 多因素方差分析 • 案例研究 • 总结与展望
01 引言
主题简介
两因素及多因素方差分析
在生物统计中，两因素及多因素方差分析是用来比较不同组之间的 平均值是否存在显著差异的统计方法。
适用场景
适用于研究两个或多个因子对响应变量的影响，例如药物剂量和治 疗效果、不同品种和产量等。
详细描述
例如，比较不同饲料类型和不同饲养环境下 猪的增重效果。将猪随机分为不同的组，每 组给予一种饲料并处于一种饲养环境，然后 比较各组的平均增重。
多因素方差分析案例
总结词
多因素方差分析用于比较多个分类变量对数值型变量的影响。
详细描述
例如，比较不同饲料类型、不同饲养环境以及不同品种的猪的增重效果。将猪随机分为 不同的组，每组给予一种饲料、处于一种饲养环境并属于一个品种，然后比较各组的平
基本思想
通过比较各组间的方差与误差方差，判断不同组间是否存在显著差 异。
课程目标和意义
掌握两因素及多因素方差分析的基本原理和步骤
通过学习，学生应能够理解两因素及多因素方差分析的基本概念、原理和实施步骤，为进一步应用和拓展打下基础。
培养解决实际问题的能力
学习两因素及多因素方差分析的目的是为了解决实际问题，如探究不同处理对实验结果的影响、比较不同组间的差异 等。通过学习和实践，学生应能够运用该方法解决实际问题。
03
研究方差分析在不同领域的应用，如医学、生物学、经济学和社会科 学等。
04
开发更高效的算法和软件，以方便用户进行方差分析和相关统计计算。
THANKS FOR WATCHING
感谢您的观看
均增重。

SPSS超详细操作：两因素多元方差分析(Two

SPSS超详细操作：两因素多元方差分析(Two

SPSS超详细操作：两因素多元方差分析(Two医咖会在之前的推文中，推送过多篇方差分析相关的文章，包括：单因素方差分析(One-Way ANOVA)双因素方差分析(Two-way ANOVA)三因素方差分析(Three-way ANOVA)单因素重复测量方差分析两因素重复测量方差分析三因素重复测量方差分析单因素多元方差分析(One-way MANOVA)每种方差分析的应用场景，以及该如何进行SPSS操作和解读结果，各位伙伴请点击相应的文章链接查看~~今天，我们再来介绍一种统计方法：两因素多元方差分析(Two-way Manova)。

一、问题与数据某研究者想研究三种干预方式（regular—常规干预；rote—死记硬背式干预；reasoning—推理式干预）对学生学习成绩的影响。

研究者记录了学生两门考试的成绩：文科成绩（humanities_score）和理科成绩（science_score）。

另外，基于之前的知识，研究者假设干预方式对男女两种性别学生的效果可能不同。

换言之，研究者想知道不同干预方式对学习成绩的影响在男女学生中是否不同。

也就是说，干预方式和性别两个自变量之间是否存在交互作用（interaction effect）。

注：交互作用是指某一自变量对因变量的效应在另一个自变量的不同水平会不同。

在本例中，就是要比较①男性中干预方式对学习成绩的影响和②女性中干预方式对学习成绩的影响。

这两个效应就成为单独效应（simple main effects），也就是说，单独效应是指在一个自变量的某一水平，另一个自变量对因变量的影响。

因此，交互作用也可以看做是对单独效应间是否存在差异的检验。

在本研究中，共有三个效应：性别的主效应；干预方式的主效应；性别和干预方式的交互作用。

研究者选取30名男学生和30名女学生，并将其随机分配到三个干预组中，每个干预组中共有10名男学生和10名女学生。

部分数据如下：二、对问题的分析使用两因素多元方差分析法进行分析时，需要考虑10个假设。

双因素试验方差分析

双因素试验方差分析

SS E df E
SST
注意
df E dfT df A f B , SSE SST SSA SSB
各因素离差平方和的自由度为水平数减一，总平方 和的自由度为试验总次数减一。
双因素（无交互作用）试验的方差分析表
简便计算式：
SS A DA p, SSB DB p
双因素试验的方差分析
在实际应用中，一个试验结果（试验指标）往往 受多个因素的影响。不仅这些因素会影响试验结果， 而且这些因素的不同水平的搭配也会影响试验结果。 例如：某些合金，当单独加入元素A或元素B时， 性能变化不大，但当同时加入元素A和B时，合金性 能的变化就特别显著。 统计学上把多因素不同水平搭配对试验指标的 影响称为交互作用。交互作用在多因素的方差分析 中，把它当成一个新因素来处理。 我们只学习两个因素的方差分析，更多因素的 问题，用正交试验法比较方便。
双因素无重复（无交互作用）试验资料表
因素 B 因素 A
B1
X 11 ... X a1
B2
X 12 ... X a2
... Bb
... ... ... X 1b ... X ab
Ti. X ij X i. T b i.
j 1
b
A1 ... Aa
a b i 1 j 1
1 b i ij i 水平Ai对试验结果的效应 a j 1 1 a j ij j 水平Bj对试验结果的效应 b i 1 试验误差 ij X ij ij
特性：

i 1
a
i
0;

j 1
b
j
0; ij ~ N 0,

anova方差分析

anova方差分析

anova方差分析ANOVA（Analysis of Variance，方差分析）是一种用于综合分析实验数据的方法。

它包括单因素（one-way ANOVA）、双因素（two-way ANOVA）和多因素（multi-factor ANOVA）等类型，多用于处理多组数据之间的比较。

在实验过程中，ANOVA通常用于确定影响结果的协变因素，即那些可能影响样本测量的其他条件。

它通过将样本分为不同的组，并检查这些组之间差异的大小来识别这些因素。

统计学家通常会使用“方差”这个度量值，估算组之间的差异。

以下是ANOVA方差分析的详细介绍：一、单因素ANOVA单因素ANOVA适用于只有一个因素（例如不同药物治疗方式）对样本产生影响的情况。

其假设组内方差相等，呈正态分布，且每个组之间的观测值互相独立。

所得的P值表示每个组是否具有显著差异。

二、双因素ANOVA双因素ANOVA适用于要比较两个或以上的因素对结果有影响的场景，例如，限制草料供应量和肉质品质等。

这时需要考虑组内和组间的方差，以确定实验结果是否受到影响。

并且还需要考虑这些因素之间是否有交互作用。

例如，在研究不同药物及剂量对人体的影响时，可能存在一定的相互作用。

三、多因素ANOVA多因素ANOVA指三个及以上的因素对样本测量结果的影响，常常用于生物医学领域、社会科学、市场营销等问题的研究中。

在进行多因素方差分析时，通常会同时分析主效应和相互作用效应。

四、如何解释ANOVA分析结果？ANOVA分析产生的主要输出是总体平均数和方差共享数据之间的显著性。

通过计算F值，ANOVA可以给出基于样本的判断，我们可以决定差异的可靠程度。

如果发现具有显著性，则意味着有些因素比其他因素更可能对实验结果产生影响，并且根据相关假设，可以推导出某一特定因素是关键因素。

如果发现因素之间存在交互作用，则意味着在控制每个因素的效应时，其余因素对实验结果产生了额外的影响。

二因素分析知识点总结

二因素分析知识点总结

二因素分析知识点总结在进行二因素分析时，我们通常会考虑两个变量之间的关系。

这两个变量可以是不同的事物、事件或者现象，我们希望通过研究它们之间的关系来获取更深层次的理解。

二因素分析能够帮助我们确定这两个变量之间是否存在相关性，以及这种相关性的强度和方向。

在进行二因素分析时，有一些重要的知识点需要了解和掌握。

在这篇文章中，我们将对二因素分析的一些关键知识点进行总结和梳理，以便更好地理解和应用这一统计方法。

一、二因素分析的基本概念1. 因素：在二因素分析中，我们所考虑的两个变量就是我们研究的因素。

这两个因素可以是任何可以被测量和观察的变量，比如温度和湿度、产品质量和产品价格、广告投入和销售额等。

2. 可变因素和控制因素：在进行二因素分析时，我们需要区分出两个因素中的哪一个是自变量，哪一个是因变量。

自变量称为可变因素，它是我们想要观察和操纵的或被操作的变量；而因变量称为控制因素，它是由自变量影响的或者是需要预测的变量。

3. 相关性：在进行二因素分析时，我们通常希望确定两个因素之间是否存在相关性。

相关性指的是两个变量之间的关联程度，通常用相关系数（Correlation Coefficient）来表示。

相关系数的取值范围在-1和1之间，0表示没有相关性，1表示完全正相关，-1表示完全负相关。

4. 方差分析：在进行二因素分析时，我们通常会使用方差分析来确定两个因素之间是否存在显著的差异。

方差分析是一种统计方法，用于比较两个或多个组之间的均值是否存在显著差异，以判断因素是否会对结果产生影响。

5. 交互作用：在进行二因素分析时，我们还需要考虑两个因素之间是否存在交互作用。

交互作用指的是两个因素之间关系的变化是否受到另一个因素的影响。

在分析交互作用时，我们通常需要通过相交的效应图（Interaction Plot）或者交互效应检验（Interaction Effect Test）来确定。

二、二因素分析的常见方法1. 双因素方差分析：双因素方差分析是一种常见的二因素分析方法，用于比较两个或多个组之间的均值是否存在显著差异。

第九章两因素及多因素方差分析

第九章两因素及多因素方差分析

ab
x..k
xijk
i1 j1
abn
x...
xijk
i1 j1 k 1
i 1, 2,..., a j 1, 2,...,b k 1, 2,..., n
离差平方和的分解
aa
SSSSTT
bb
nn ((xxiijjkk xx...... ))22
ii11 jj11 kk 11
4 -149
-10
131
153
解：
根据经验，密度与施肥量之间不存在交互作用
C x.2. 3922 9604.0 ab 16
ab
SST
xi2j C 246868 9604.0 237264.0
i1 j1
SS A
1 b
a i 1
xi2.
C
74862 4
9604.0
9111.5
SSB
HA : 1，2， ，b不全为0
第二步：提出零假设和备择假设
要说明两个因素的交互作用是否显著：
H0 : ( )11 12 ( )ab 0 HA : ( )11，( )12， ，( )ab不全为0
第三步：计算统计量
平方和的简易计算法：
SST
a i 1
bn
SST
j1 k 1
a
xi2jk i 1
发酵实验方差分析表
变差来源 原料 A 温度 B
AB 误差 总和
平方和 1554.17 3150.58 808.75 1656.50 7170.00
自由度 2 2 4
27 35
均方 777.09 1575.29 202.19 61.35
F 12.67** 25.68** 3.30*

Stata软件操作教程 (9)

Stata软件操作教程 (9)
令语句，sales是将要分析的变量，color是分类变量， 也就是水平变量，tabulate选项的作用是产生有关数据 的汇总表。显示结果如图4.1所示。
实验4.2双因素或多因素方差分析
一、实验基本原理 在现实研究中，一个事件不可能仅受一个因素的影响，
恰恰相反，一个事件是受多个因素综合作用的结果， 所以多因素方差分析相比单因素方差分析有更广泛的 应用空间。下面以双因素方差分析中无交互作用的情 况为例，介绍一下多因素方差分析的基本原理。
例如，利用sales.dta数据做方差分析的练习，在这个 数据中，反映了一种饮料的销售情况，这种饮料有4种 颜色，在5家超市进行销售，除颜色之外其他条件全部 相同，分析一下饮料的颜色是否对销售量有影响。
对此问题进行差分析的命令语句为：
oneway sales color, tabulate 这个命令语句中，oneway是进行单因素方差分析的命
一般情况下，双因素方差分析的数据如表4.3所示排列， 影响因素有A和B两个。
二、实验数据和实验内容 实验数据来源于对某国女性工作情况的调查，
其中变量married是代表是否结婚的分类变 量，children是代表是否拥有子女的分类变 量，wage代表工资水平。完整的数据在本 书附带光盘的data文件夹的“wwork.dta” 工作文件中。
习题
1.利用usaauto.dta数据进行单因素方差分析，分析内 容为美国汽车的价格price是否受进口还是国产的影响， 即以price为因变量，以foreign为分类变量进行单因素 分析，并且进行结果的解读。
2.利用womenwork.dta数据进行多因素方差分析，分 析内容为妇女受教育水平education是否受结婚 married和是否有子女children以及二者交互项的影响， 即以education为因变量，以married、children和 married*children为自变量进行多因素分析，并且进行 结果的解读。

双因素方差分析方法

双因素方差分析方法

(
)
dfT , df A , df B , df E ,则
SS A df A MS A = ~ F ( ( a 1) , ( a 1)( b 1) ) FA = SS E df E MS E
SS B df B MS B = ~ F ( ( b 1) , ( a 1)( b 1) ) FB = SS E df E MS E
结论:工人对产品的产量有显著影响, 结论:工人对产品的产量有显著影响, 机器对产品的产量有极显著影响. 机器对产品的产量有极显著影响.
例1的上机操作 的上机操作
原始数据,行因素水平, 原始数据,行因素水平,列因素水平
对应例1 对应例 的数据输入方式
工人对产品产量有显著影响,而机器对产品产量的影响极显著. 工人对产品产量有显著影响,而机器对产品产量的影响极显著.
1 b 水平A α i = ∑ ij = i i 水平 i对试验结果的效应 a j =1 1 a 水平 β j = ∑ ij = i j 水平Bj对试验结果的效应 b i =1 试验误差 ε ij = X ij ij
特性: 特性:
∑ α i = 0;
i =1
a
β j = 0; ε ij ~ N ( 0, σ 2 ) ∑
SST = ∑∑ X ij X
i =1 j =1
a
b
(
)
2
可分解为: 可分解为:SST = SS A + SS B + SS E
SS A = b∑ X i. X
SS B = a ∑ X . j X
j =1 a b
a
i =1 b
(
)
2
称为因素A的离差平方和, 称为因素 的离差平方和, 的离差平方和 对试验指标的影响. 反映因素 A 对试验指标的影响. 称为因素B的离差平方和, 称为因素 的离差平方和, 的离差平方和 对试验指标的影响. 反映因素 B 对试验指标的影响.

10.3(双因素方差分析)

10.3(双因素方差分析)

10.3.1 无交互作用的双因素方差分析
计算F统计量 在单元格G15中输入公式： 中输入公式： 计算 统计量FB，在单元格 统计量 中输入公式 =F15/F16 计算F 中输入公式： 计算 A的P值，在单元格 值 在单元格H14中输入公式： 中输入公式 =FDIST(G14,D14,D16) 计算FB的P值，在单元格 中输入公式： 计算 值 在单元格H15中输入公式： 中输入公式 =FDIST(G15,D15,D16) 如图10.9所示． 所示． 如图 所示
平均值
x1..
x2..
xl..
10.3 双因素方差分析
10. 10.3.1 无交互作用的双因素方差分析
无交互作用的双因素方差分析的数学模型可以表示 为： xijk= µ + αi + τj + εijk
ε ijk ~ N (0, σ 2 ) , 且相互独立. 1≤i≤l, 1≤j≤m, 1≤k≤n 且相互独立
10.3.1 无交互作用的双因素方差分析
( 2) 计算 xi ..，在单元格 在单元格C10中输入公式： 中输入公式： 中输入公式 =AVERAGE(C4:C9) 并将单元格C10中公式复制到单元格区域 中公式复制到单元格区域D10:F10． 并将单元格 中公式复制到单元格区域 ． 在单元格G4中输入公式 中输入公式： 计算x. j . ，在单元格 中输入公式： =AVERAGE(C4:F5) 并将单元格G4中公式复制到单元格 、 中 并将单元格 中公式复制到单元格G6、G8中． 中公式复制到单元格 如图所示． 如图所示．
10.3 双因素方差分析 对于两因素问题，通常考虑等重复观测的情形， 对于两因素问题 ，通常考虑等重复观测的情形，若 第一个因素A有 个水平 第二个因素B有 个水平 个水平， 个水平． 第一个因素 有l个水平，第二个因素 有m个水平．在 因素A的第 个水平和因素B的第 个水平下均进行了n次 因素 的第i个水平和因素 的第j个水平下均进行了 次 的第 个水平和因素 的第 个水平下均进行了 观测，记为{x 观测，记为 ijk，1≤i≤l，1≤j≤m，1≤k≤n}． ， ， ． 其数据结构如表所示． 其数据结构如表所示．

双因素试验的方差分析

双因素试验的方差分析

设：
X ijk ~ N ij , 2 , i 1,2,, r, j 1,2,, s, k 1,2,, t ,
各


X ijk
独立， ij , 2 均为未知参数。或写成：
2 ijk ~ N 0, , 各 ijk 独立 i 1,2,, r , j 1,2,, s, k 1,2,, t.
双因素试验的方差分析
影响试验结果的因素不止一个，要用双因素
或 多因素的方差分析；
确定哪些因素是主要的，它们对试验结果的
影响是否显著； 它们之间是否有交互作用。
（一）双因素等重复试验（有交互作用）的方差分析设有两个因
素A，B作用于试验的指标。 因素A有r个水平
因素B有s个水平
A1 , A2 ,, Ar
X . j.
1 r t X ijk , j 1,2,, s. rt i 1 k 1
总偏差平方和（称为总变差）
ST X ijk X .
2 i 1 j 1 k 1 r s t


ST写成：
S T X ijk X
i 1 j 1 k 1 s t r


1 1319 .82 2 2 2 S A B 110.8 91.9 90.1 2 24 S A S B 1768 .69250 , S E ST S A S B S A B 236.95000 .


得方差分析表如下：
表9.11 例1的方差分析表 方差来源 平方和 自由度 均 方 F 值
A1 A2
X 121 , X 122, , X 12t
…
X 211 , X 212, X 221 , X 222, , X 21t , X 22t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a
2
A因素误差平方和 SSA bn yi y
i 1
B因素误差平方和
b
SSB an
2
y j y
j1
AB交互作用误差平方和
a b
SSAB n
yij yi y j y 2
i1 j1
2、提出假设
H01：i 0, H A1：i 0 H02：i 0, H A2：i 0 H03：（ ）ij 0，HA3：（ ）ij 0，其中i 1,2，...,a; j 1,2，...,b
3、检验统计量的计算
在F检验时，A因素、B因素和互作效应的检验统计量均以 MSe做分母：FA=MSA/MSe FB=MSB/MSe FAB=MSAB/MSe
其中表示所有观测值的总平均数
i 表示因素A第i水平的处理效应

表示
j
因素B第j水平的处理效应
ij 表示因素A的第i水平和因素B第i水平的交互效应
ijk表示随机误差
（三）平方和与自由度的分解
1、平方和的分解
总平方和SST被分解为A因素所引起的平方和SSA、 B因素所引起的平方和SSB、AB交互作用所引起 的平方和SSAB、误差平方和SSe
4、有交互作用的双因素方差分析或可重复双因素方 差分析 (Two-factor with replication)：如果两个因 素对试验数据的单独影响外，两个因素的搭配还 会对结果产生一种新的影响。
二、双因素交叉分组试验设计的描述
（一）双因素试验的数据描述 （二）观测值的描述 （三）平方和与自由度的分解 （四）平方和的简便计算公式 （五）各项均方的计算
3、检验统计量的计算
MS AB

SS AB df A

SS AB
a -1b -1
MSe

SSe dfe

SSe ab（n -1）
第二节 不同实验类型的双因素方差分析
一、固定模型
（一）重复试验时的双因素方差分析 1、观察值的线性统计模型 yijk i j i j i jk，其中i 1,2，...a; j 1,2，...b;k 1,2，...n;
┆
…
┆
Aa 和
ya11 ya12 ┆ ya1n
y.1.
ya21 ya22 ┆ ya2n
y.2.
… …
yab1 yab2 ┆ yabn
y.b.
和 y1..
y2.. ┆ ya.. y…
（二）观测值的描述
对于上表中的每一个观测值可用线性统计模型描述
yijk i j ij ijk
（四）平方和的简便计算方式
abn
SST
y2 ij k

C
i1 j1 k 1
a
SS A

1 bn
y2 i

C
i1
b
SS B

1 an
y2 j

C
j1
a b
SSAB n
yij yi y j y 2
i1 j1
SSe
随机误差项平方和
a bn
SSe
（y ij k

y
）2
ij
i1 j 1 k 1
2、平方和的分解
与平方和相应的自由度分别为： 总自由度：dfT=abn-1 A因素处理间自由度：dfA=a-1 B因素处理间自由度：dfB=b-1 交互作用自由度：dfAB=(a-1)(b-1) 处理内自由度：dfe=ab(n-1) dfT=dfA+dfB+dfAB+dfe
第一节 双因素方差分析概述
一、双因素试验汇中的几个基本概念
1、主效应（main effect）：各实验因素相对独立的 效应，该效应水平的改变会造成因素效应的改变， 如包装方式对果汁销售量的影响。
2、互作效应（interaction）：两个或多个实验因素的 相互作用而产生的效应。
3、无交互作用的双因素方差分析或无重复双因素方 差分析(Two-factor without replication)：两个因素 对试验结果。两个因素对试验数据的影响。
第九章 双因素和多因素方差分析
学习目标
掌握：两因素交叉分组（有重复观察值、 无重复观察值）资料的方差分析方法。
熟悉：多因素试验线性模型和不同变异来 源期望均方构成。
了解：缺失数据的估计原理及方差分析方 法。
讲授内容
第一节 双因素方差分析概述 第二节 不同实验类型的双因素方差分析 第三节 多因素试验的方差分析 第四节 缺失数据的估计 第五节 数据变换
（一）试验数据的描述
A1
因素A
A2
i=1.，
2,3…，a
┆
B1 y111 y112 ┆ y11n
因素B j=1.，2,3…，b
B2
…
y121
…
y122
┆
y12n
Bb y1b1 y1b2 ┆ y1bn
y211 y212 ┆ y21n
y221 y222 ┆ y22n
…
y2b1 y2b2 ┆ y2bn
┆

a i 1
bn
y2 ij k j1 k 1

1 n
a i 1
b
y2 ij j 1
SST
SSA
SSB
SSAB
（五）各项均方的计算
MS T
SST dfT
SST abn 1
MS A

SS A B

SSB df B

SSB b 1
用F分布的上尾检验，拒绝域为F>Fα
4、均方期望
E(MSe ) 2
E(MS
A
)


2＋ bn a 1
a i 1

2 i
E (MS B
)


2＋
an b 1
a i1

2 j
E(MS AB )


2＋ （a
n 1)(b
1)
a i 1

2 ij
（二）无重复实验时的双因素方差分析
1、观测值的描述
yijk i j i j，其中i 1,2，...a; j 1,2，...b;
a
b
i 0； j 0； i j为相互独立且服从正态分布N 0， 2 的随机变量
i1
j1
2、提出假设
H01：i 0, HA1：i 0 H02：i 0, HA2：i 0