普氏理论

普氏理论1. 普氏理论的基本假定普氏理论在自然平衡拱理论的基础上，作了如下的假设：（1） 岩体由于节理的切割，经开挖后形成松散岩体，但仍具有一定的粘结力；（2） 硐室开挖后，硐顶岩体将形成一自然平衡拱。

在硐室的侧壁处，沿与侧壁夹角为45-2φ︒的方向产生两个滑动面，其计算简图如图1所示。

而作用在硐顶的围岩压力仅是自然平衡拱内的岩体自重。

1e 2图1 普氏围岩压力计算模型（3） 采用坚固系数f 来表征岩体的强度。

其物理意为：tan c f σφτσ==+但在实际应用中，普氏采用了一个经验计算公式，可方便地求得f 值。

即10c R f = 式中 Rc ——单轴抗压强度（MPa ）。

f —— 一个量纲为1的经验系数，在实际应用中，还得同时考虑岩体的完整性和地下水的影响。

（4） 形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2. 普氏理论的计算公式（1） 自然平衡拱拱轴线方程的确定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱内岩体的自重。

先假设拱周线是一条二次曲线，如图2所示。

在拱轴线上任取一点M （x,y ），根据拱轴线不能承受拉力的条件，则所有外力对M 点的弯矩应为零。

即202qx Ty -= （a ） 式中 q ——拱轴线上部岩体的自重所产生的均布荷载； T ——平衡拱拱顶截面的水平推力；x ，y ——分别为M 点的x ，y 轴坐标。

上述方程中有两个未知数，还需建立一个方程才能求得其解。

由静力平衡方程可知，上述方程中的水平推力T 与作用在拱脚的水平推xOT图2 自然平衡拱计算简图力T ＇数值相等，方向相反。

即T=T ＇由于拱脚很容易产生水平位移而改变整个拱的内力分布，因此普氏认为拱脚的水平推力T ＇必须满足下列要求T ＇≤qa 1f （b ）即作用在拱脚处的水平推力必须小于或者等于垂直反力所产生的最大摩擦力，以便保持拱脚的稳定。

普氏理论和太沙基理论 Document serial number【LGGKGB-LGG98YT-LGGT8CB-LGUT-普氏理论1. 普氏理论的基本假定普氏理论在自然平衡拱理论的基础上，作了如下的假设：（1） 岩体由于节理的切割，经开挖后形成松散岩体，但仍具有一定的粘结力； （2） 硐室开挖后，硐顶岩体将形成一自然平衡拱。

在硐室的侧壁处，沿与侧壁夹角为45-2φ︒的方向产生两个滑动面，其计算简图如图1所示。

而作用在硐顶的围岩压力仅是自然平衡拱内的岩体自重。

图1 普氏围岩压力计算模型（3） 采用坚固系数f 来表征岩体的强度。

其物理意为：但在实际应用中，普氏采用了一个经验计算公式，可方便地求得f 值。

即 式中 Rc ——单轴抗压强度（MPa ）。

f —— 一个量纲为1的经验系数，在实际应用中，还得同时考虑岩体的完整性和地下水的影响。

（4） 形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2. 普氏理论的计算公式（1） 自然平衡拱拱轴线方程的确定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱内岩体的自重。

先假设拱周线是一条二次曲线，如图2所示。

在拱轴线上任取一点M （x,y ），根据拱轴线不能承受拉力的条件，则所有外力对M 点的弯矩应为零。

即202qx Ty -= （a ） 式中 q ——拱轴线上部岩体的自重所产生的均布荷载；T ——平衡拱拱顶截面的水平推力；x ，y ——分别为M 点的x ，y 轴坐标。

上述方程中有两个未知数，还需建立一个方程才能求得其解。

由静力平衡方程可知，上述方程中的水平推力T 与作用在拱脚的水平推图2 自然平衡拱计算简图力T ＇数值相等，方向相反。

即T=T ＇由于拱脚很容易产生水平位移而改变整个拱的内力分布，因此普氏认为拱脚的水平推力T ＇必须满足下列要求T ＇≤qa 1f （b ）即作用在拱脚处的水平推力必须小于或者等于垂直反力所产生的最大摩擦力，以便保持拱脚的稳定。

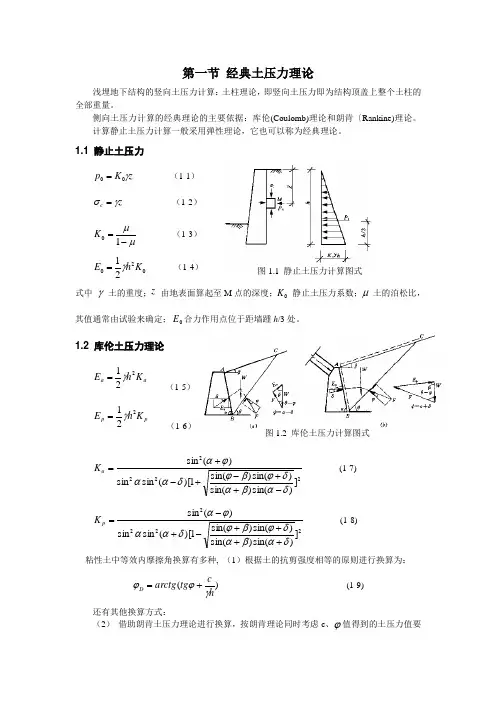
第一节 经典土压力理论浅埋地下结构的竖向土压力计算：土柱理论，即竖向土压力即为结构顶盖上整个土柱的全部重量。

侧向土压力计算的经典理论的主要依据：库伦(Coulomb)理论和朗肯〔Rankine)理论。

计算静止土压力计算一般采用弹性理论，它也可以称为经典理论。

1.1 静止土压力z K p γ00= （1-1）z c γσ= （1-2）μμ-=10K （1-3）02021K h E γ= （1-4）式中 γ-土的重度；z -由地表面算起至M 点的深度；0K -静止土压力系数；μ-土的泊松比，其值通常由试验来确定；0E 合力作用点位于距墙踵h /3处。

1.2 库伦土压力理论aa K h E 221γ= （1-5） p p K h E 221γ=（1-6）2222])sin()sin()sin()sin(1)[(sin sin )(sin δαβαδϕβϕδααϕα-++-+-+=a K (1-7) 2222])sin()sin()sin()sin(1)[(sin sin )(sin δαβαδϕβϕδααϕα++++-+-=p K (1-8) 粘性土中等效内摩擦角换算有多种, （1）根据土的抗剪强度相等的原则进行换算为：)(hctg arctg D γϕϕ+= (1-9) 还有其他换算方式：（2） 借助朗肯土压力理论进行换算，按朗肯理论同时考虑c 、ϕ值得到的土压力值要图1.1 静止土压力计算图式图1.2 库伦土压力计算图式和已换算成等效内摩擦角D ϕ后得到的土压力值相等，推算得到等效内摩擦角D ϕ。

（3）采用《建筑地基基础设计规范》计算。

1.3 朗肯土压力理论z z γσ= （1-10）z K x γσ0= （1-11）a a a K c zK p 2-=γ （1-12） P P P K c zK p 2+=γ （1-13）式中：)245(2ϕ-=tg K a ，)245(2ϕ+=tg K pγγ222221c K ch K h E a a a +-= （1-14） 图1.3 朗肯极限平衡状态第二节 地下结构的土层压力中南大学资源与安全学院 赵建平2.1 浅埋地下结构的竖向土层压力在软土地层中当地下结构物采用明挖法施工，埋置深度较浅(顶盖离地表面距离较近时)，称为浅埋地下结构。

普氏理论1. 普氏理论的基本假定普氏理论在自然平衡拱理论的基础上，作了如下的假设：（1） 岩体由于节理的切割，经开挖后形成松散岩体，但仍具有一定的粘结力；（2） 硐室开挖后，硐顶岩体将形成一自然平衡拱。

在硐室的侧壁处，沿与侧壁夹角为45-2φ︒的方向产生两个滑动面，其计算简图如图1所示。

而作用在硐顶的围岩压力仅是自然平衡拱内的岩体自重。

图1 普氏围岩压力计算模型（3） 采用坚固系数f 来表征岩体的强度。

其物理意为：但在实际应用中，普氏采用了一个经验计算公式，可方便地求得f 值。

即式中 Rc ——单轴抗压强度（MPa ）。

f —— 一个量纲为1的经验系数，在实际应用中，还得同时考虑岩体的完整性和地下水的影响。

（4） 形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2. 普氏理论的计算公式（1） 自然平衡拱拱轴线方程的确定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱内岩体的自重。

先假设拱周线是一条二次曲线，如图2所示。

在拱轴线上任取一点M （x,y ），根据拱轴线不能承受拉力的条件，则所有外力对M 点的弯矩应为零。

即202qx Ty -= （a ） 式中 q ——拱轴线上部岩体的自重所产生的均布荷载；T ——平衡拱拱顶截面的水平推力；x ，y ——分别为M 点的x ，y 轴坐标。

上述方程中有两个未知数，还需建立一个方程才能求得其解。

由静力平衡方程可知，上述方程中的水平推力T 与作用在拱脚的水平推图2 自然平衡拱计算简图力T ＇数值相等，方向相反。

即T=T ＇由于拱脚很容易产生水平位移而改变整个拱的内力分布，因此普氏认为拱脚的水平推力T ＇必须满足下列要求T ＇≤qa 1f （b ）即作用在拱脚处的水平推力必须小于或者等于垂直反力所产生的最大摩擦力，以便保持拱脚的稳定。

此外，普氏为了安全，又将水平推力降低一半后，令T= qa 1f/2，代入（a ）式可得拱轴线方程为显然，拱轴线方程是一条抛物线。

普氏天然拱理论
普氏天然拱理论是由美国科学家威廉·普氏于1879年提出的一种理论，它提出了一种新的拱形结构，可以更有效地支撑建筑物的重量。

普氏天然拱理论的基本思想是，建筑物的重量可以通过一种叫做“天然拱”的结构来支撑，而不是通过传统的拱形结构。

普氏天然拱理论的核心思想是，建筑物的重量可以通过一种叫做“天然拱”的结构来支撑，而不是通过传统的拱形结构。

这种结构的特点是，它的拱形结构是由一系列的支撑柱和拱顶组成的，支撑柱的位置和形状可以根据建筑物的重量和结构来调整，从而使建筑物更加稳定。

普氏天然拱理论的另一个优点是，它可以更有效地利用建筑物的空间，因为它可以更好地利用建筑物的空间，而不会影响建筑物的结构。

此外，普氏天然拱理论还可以更有效地利用建筑物的材料，因为它可以更好地利用建筑物的材料，而不会影响建筑物的结构。

普氏天然拱理论的应用非常广泛，它可以用于建筑物的支撑，也可以用于桥梁、隧道、港口等建筑物的支撑。

它的应用不仅可以提高建筑物的稳定性，还可以提高建筑物的使用寿命。

总之，普氏天然拱理论是一种非常有效的建筑支撑理论，它可以更有效地支撑建筑物的重量，更有效地利用建筑物的空间和材料，并且可以提高建筑物的稳定性和使用寿命。

普氏地压理论
普氏地压理论是简称“普氏理论”的古典物理学理论，是第一个解释重力力学的理论，由普鲁士物理学家施特劳斯·卡尔·普氏（Carl Friedrich Gauss）1809年发表，已有200多年历史。

普氏理论认为，地球表面受地球内部质量分布的作用，表面弯曲，可以用弧面刻画出一个低压弧，以此来解释地球各点处引力的强弱之分。

根据普氏理论，地球表面各点外向的重力是由地面处弯曲的地形所决定的，也就是说，当地面位于低压弧的段落的时候，地面的重力会受到抵消而减少，而在高压弧的段落里，地面的重力就会受到增加的影响。

从这个角度上说，地球表面的形状非常重要，它决定了重力的分布。

普氏理论是一个历史悠久且影响深远的理论，它极大地发展了我们进行地理测量，地形分析，重力场研究等相关领域的能力，而且也为地质圈、大气圈以及磁场的研究奠定了物理理论基础。

今天，普氏理论仍被用于地球测量，地形的解析，重力场的探测，磁场的探测等研究领域，被广泛采用。

总之，普氏理论始终是先进物理学理论中最重要的一部分，其研究结果也帮助我们更好地解释地球上发生的许多科学事件。

一、普氏系数的确定
二、硐室围岩压力
注:1、2、主要参考：肖树芳、杨淑碧编，1987，岩体力学，地质出版社，P125-133。

侧向压力P h 按朗金主动土压理论进行计算；
P 0为仅考虑硐室两侧岩体在较大压力作用下向硐内挤入时形成的底部围岩压力。

普氏理论计算围岩压力
适用条件:假设岩体为不具有内聚力的松散体,如断裂破碎带或强风化带内岩体.
f 值一般可根据岩石单轴抗压强度来确定，即f =σc /100；也可根据类比法与经验确定。

各种岩石 的f 值的经验数值列于下页附表1。

实际工作中可以根据前期塌腔形状反推该类围岩的f 值。

当岩石性质较差（例如当f <2时），硐室开挖后不但顶部要塌落，两侧也可能不稳定而出现向硐内的滑动，压力拱将继续扩大到以拱跨为2a 的新压力拱，此时新拱跨2a、硐顶垂直围岩压力、侧向围岩压力及由此产生的底部围岩压力按下表求取：。

一、名词解释：1、岩石力学：研究岩石的力学性状和岩石对各种物理环境的力场产生效应的一门理论科学，是力学的一个分支，同时它也是一门应用科学。

2、岩石：是由各种造岩矿物或岩屑在地质作用下按一定规律组合而成的多种矿物颗粒集合体，是组成地壳的基本物质。

3、岩体：是地质体，它的形成于漫长的地质年代有关，它是一定工程范围内的自然地质体，经过各种地质运动，内部含有构造和裂隙。

4、结构面：①指在地质历史发展过程中岩体内形成的具有一定的延伸方向和长度，厚度相对较小的宏观地质界面或带。

②又称弱面或地质界面，是指存在于岩体内部的各种地质界面，包括物质分异面和不连续面，如假整合、不整合、褶皱、断层、层面、节理和片理等。

5、岩石结构：结构面和结构体在岩体内的排列组合形式，称为岩体结构。

6、软化系数：指岩石试件的饱和抗压强度与干燥状态下的抗压强度的比值7、弹性模量：弹性范围内轴向应力与轴向应变之比。

8、变形模量：岩石在单轴压缩条件下，轴向应力与轴向应变之比。

9、泊松比：岩石在单向受压条件下，横向应变与纵向应变之比10、抗压强度：是指岩石试件在单轴压力下达到破坏的极限值。

11、抗拉强度：是指岩石试件在单向拉伸条件下试件达到破坏的极限值。

12、抗剪强度：是指岩石抵抗剪切破坏的能力13、流变性：指在外界条件不变时，岩石应变或应力随时间而变化的性质。

14、蠕变：在大小和方向都保持不变的外力作用下，变形随时间不断增长的现象。

15、准岩体强度：考虑裂隙发育程度，经过修正后的岩石强度称为准岩体强度。

16、完整性系数：是岩体中纵波速度和同种岩体的完整岩石中纵波速度之平方比。

17、普氏系数：岩石单轴抗压强度的十分之一。

18、RQD ：指大于10cm 的岩芯累计长度与钻孔进尺长度之比的百分数。

19、原岩应力：岩石是地球表层的物质，在漫长的地质年代里，由于地质构造运动等原因使地壳物质产生了内应力效应在，这种应力称为地应力或原岩应力。

20、自重应力：由于岩体自重而产生的天然应力叫自重应力。