泰沙基理论与公式

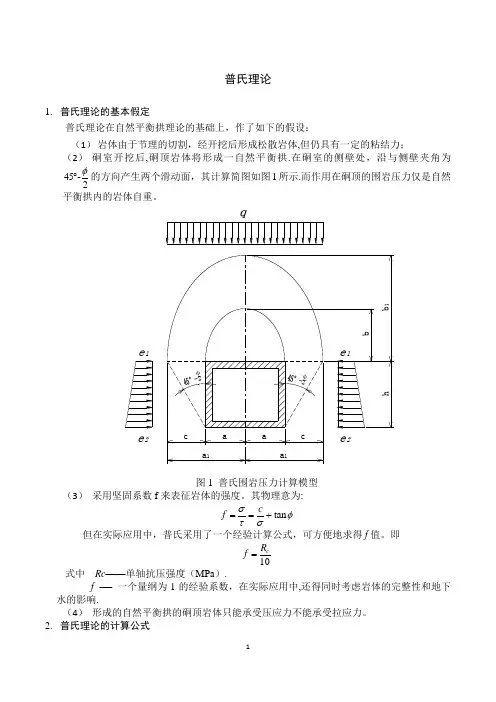
普氏理论1. 普氏理论的基本假定普氏理论在自然平衡拱理论的基础上，作了如下的假设：（1） 岩体由于节理的切割，经开挖后形成松散岩体,但仍具有一定的粘结力；（2） 硐室开挖后,硐顶岩体将形成一自然平衡拱.在硐室的侧壁处，沿与侧壁夹角为45-2φ︒的方向产生两个滑动面，其计算简图如图1所示.而作用在硐顶的围岩压力仅是自然平衡拱内的岩体自重。

1e 2图1 普氏围岩压力计算模型（3） 采用坚固系数f 来表征岩体的强度。

其物理意为:tan c f σφτσ==+ 但在实际应用中，普氏采用了一个经验计算公式，可方便地求得f 值。

即10c R f = 式中 Rc ——单轴抗压强度（MPa ）.f -— 一个量纲为1的经验系数，在实际应用中,还得同时考虑岩体的完整性和地下水的影响.（4） 形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2. 普氏理论的计算公式（1） 自然平衡拱拱轴线方程的确定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱内岩体的自重。

先假设拱周线是一条二次曲线，如图2所示。

在拱轴线上任取一点M （x ，y ），根据拱轴线不能承受拉力的条件，则所有外力对M 点的弯矩应为零。

即202qx Ty -= (a ） 式中 q ——拱轴线上部岩体的自重所产生的均布荷载；T-—平衡拱拱顶截面的水平推力；x,y ——分别为M 点的x ，y 轴坐标。

上述方程中有两个未知数,还需建立一个方程才能求得其解。

由静力平衡方程可知,上述方程中的水平推力T 与作用在拱脚的水平推xOT图2 自然平衡拱计算简图力T ＇数值相等，方向相反。

即T=T ＇由于拱脚很容易产生水平位移而改变整个拱的内力分布,因此普氏认为拱脚的水平推力T ＇必须满足下列要求T ＇≤qa 1f （b ）即作用在拱脚处的水平推力必须小于或者等于垂直反力所产生的最大摩擦力，以便保持拱脚的稳定。

地基承载力计算公式（附小桥涵地基承载力检测）【摘要】简明列出太沙基、汉森、魏锡克、梅耶霍夫、沈珠江、普兹列夫斯基、王长科等地基承载力理论计算公式。

下面用TXT文本简明列出太沙基、汉森、魏锡克、梅耶霍夫、沈珠江、普兹列夫斯基、王长科等地基承载力理论计算公式，供参考使用。

适于标准受压，只考虑基础宽度、超载影响，不考虑其他诸如倾斜等因素。

1、太沙基（Terzaghi）地基极限承载力qu公式qu=c*Nc+q*Nq+0.5*γ*B*Nγ其中Nc=(Nq-1)*cotφNq=exp(π*tanφ) * tan²(45+φ/2)Nγ= 6 * φ / (40 -φ)式中c、φ分别表示土的粘聚力、内摩擦角，B表示基础宽度。

以下同。

2、汉森（Hansen）地基极限承载力qu公式qu=c*Nc+q*Nq+0.5*γ*B*Nγ其中Nc=(Nq-1)*cotφNq=exp(π*tanφ) * tan²(π/4+φ/2)Nγ = 1.5 * Nc * tan²φ3、梅耶霍夫（Meyerhof）地基极限承载力qu公式qu=c*Nc+q*Nq+0.5*γ*B*Nγ其中Nc=(Nq-1) * cotφNq=exp(π*tanφ)*tan²(π/4+φ/2)Nγ = (Nq - 1) * tan(1.4 * φ)4、魏锡克（Vesic）地基极限承载力qu公式qu=c*Nc+q*Nq+0.5*γ*B*Nγ其中Nc=(Nq-1) * cotφNq=exp(π*tanφ) * tan²(π/4+φ/2)Nγ = 2 * (Nq + 1) * tanφ5、沈珠江地基极限承载力qu公式qu= (1 + d / B) ^ (1 / 3) * (c / tanφ * (Nq - 1) + 0.5 * γ * b * Nγ)其中Nq=exp(π*tanφ)*tan²(π/4+φ/2)Nγ = (Nq - 1) * sinφ6、普兹列夫斯基临塑荷载pcr和临界荷载p(1/4)pcr= Mc * c + Mq * qp(1/4)= Mc * c + Mq * q + (1 / 4) * Mγ* γ * B其中Mc = π/ tanφ / (1 / tanφ +φ- π/ 2)Mq = (1 / tanφ +φ+ π/ 2) / (1 / tanφ + φ- π/ 2)Mγ= π / (1 / tanφ +φ- π/ 2)经推导，广义临界荷载p(1/n)p(1/n)= Mc * c + Mq * q + (1 / n) * Mγ* γ * B7、王长科地基第一拐点承载力q1公式q1 = c * Nc + q * Nq + 0.5 * γ * B * Nγ其中Nc = 2 * tan³(45+φ/2)Nq = (tan(45+φ/2)) ^ 4Nγ = (Nq - 1) * tan(45+φ/2)小桥涵地基承载力检测《公路桥涵施工技术规范》JTJ041-2000（P28）“小桥涵的地基检验可采用直观法或触探方法，必要时可进行土质试验”。

普氏理论1.普氏理论的基本假定普氏理论在自然平衡拱理论的基础上，作了如下的假设：（1）岩体由于节理的切割，经开挖后形成松散岩体，但仍具有一定的粘结力；（2）硐室开挖后，硐顶岩体将形成一自然平衡拱。

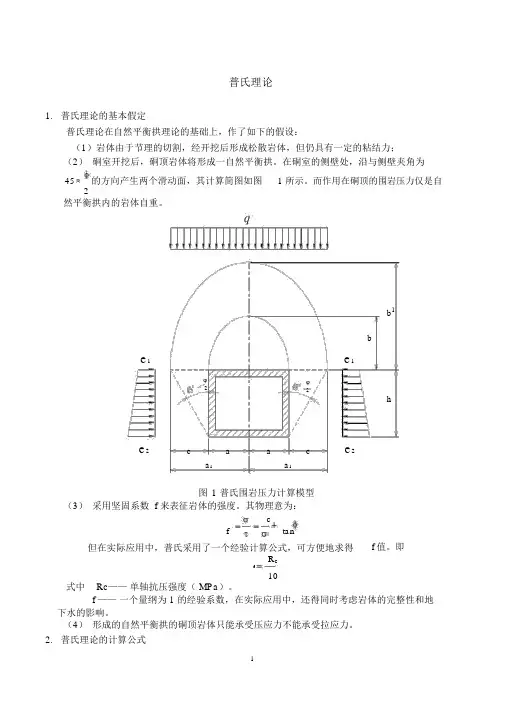
在硐室的侧壁处，沿与侧壁夹角为45 -的方向产生两个滑动面，其计算简图如图 1 所示。

而作用在硐顶的围岩压力仅是自2然平衡拱内的岩体自重。

b1be1e1φφ22he2c a a c e2a1a1图1 普氏围岩压力计算模型（3）采用坚固系数 f 来表征岩体的强度。

其物理意为：f ctan但在实际应用中，普氏采用了一个经验计算公式，可方便地求得 f 值。

即R cfRc——单轴抗压强度（ MPa）。

10式中f ——一个量纲为 1 的经验系数，在实际应用中，还得同时考虑岩体的完整性和地下水的影响。

（4）形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2.普氏理论的计算公式（1）自然平衡拱拱轴线方程的确定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱内岩体的自重。

先假设拱周线是一条二次曲线，如图 2 所示。

在拱轴线上任取一点 M（ x,y），根据拱轴线不能承受拉力的条件，则所有外力对 M 点的弯矩应为零。

即qx2（a）Ty02式中q——拱轴线上部岩体的自重所产生的均布荷载；T——平衡拱拱顶截面的水平推力；x，y——分别为 M 点的 x，y 轴坐标。

上述方程中有两个未知数，还需建立一个方程才能求得其解。

由静力平衡方程可知，上述方程中的水平推力 T 与作用在拱脚的水平推x OTyT＇φM b1xa1qa1y图 2 自然平衡拱计算简图力 T＇数值相等，方向相反。

即T=T ＇由于拱脚很容易产生水平位移而改变整个拱的内力分布，因此普氏认为拱脚的水平推力 T＇必须满足下列要求T＇≤ qa1f（b）即作用在拱脚处的水平推力必须小于或者等于垂直反力所产生的最大摩擦力，以便保持拱脚的稳定。

普氏理论和太沙基理论 Document serial number【LGGKGB-LGG98YT-LGGT8CB-LGUT-普氏理论1. 普氏理论的基本假定普氏理论在自然平衡拱理论的基础上，作了如下的假设：（1） 岩体由于节理的切割，经开挖后形成松散岩体，但仍具有一定的粘结力； （2） 硐室开挖后，硐顶岩体将形成一自然平衡拱。

在硐室的侧壁处，沿与侧壁夹角为45-2φ︒的方向产生两个滑动面，其计算简图如图1所示。

而作用在硐顶的围岩压力仅是自然平衡拱内的岩体自重。

图1 普氏围岩压力计算模型（3） 采用坚固系数f 来表征岩体的强度。

其物理意为：但在实际应用中，普氏采用了一个经验计算公式，可方便地求得f 值。

即 式中 Rc ——单轴抗压强度（MPa ）。

f —— 一个量纲为1的经验系数，在实际应用中，还得同时考虑岩体的完整性和地下水的影响。

（4） 形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2. 普氏理论的计算公式（1） 自然平衡拱拱轴线方程的确定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱内岩体的自重。

先假设拱周线是一条二次曲线，如图2所示。

在拱轴线上任取一点M （x,y ），根据拱轴线不能承受拉力的条件，则所有外力对M 点的弯矩应为零。

即202qx Ty -= （a ） 式中 q ——拱轴线上部岩体的自重所产生的均布荷载；T ——平衡拱拱顶截面的水平推力；x ，y ——分别为M 点的x ，y 轴坐标。

上述方程中有两个未知数，还需建立一个方程才能求得其解。

由静力平衡方程可知，上述方程中的水平推力T 与作用在拱脚的水平推图2 自然平衡拱计算简图力T ＇数值相等，方向相反。

即T=T ＇由于拱脚很容易产生水平位移而改变整个拱的内力分布，因此普氏认为拱脚的水平推力T ＇必须满足下列要求T ＇≤qa 1f （b ）即作用在拱脚处的水平推力必须小于或者等于垂直反力所产生的最大摩擦力，以便保持拱脚的稳定。

普氏理论1. 普氏理论的根本假定普氏理论在自然平衡拱理论的根底上，作了如下的假设：（1） 岩体由于节理的切割，经开挖后形成松散岩体，但仍具有一定的粘结力；（2） 硐室开挖后，硐顶岩体将形成一自然平衡拱。

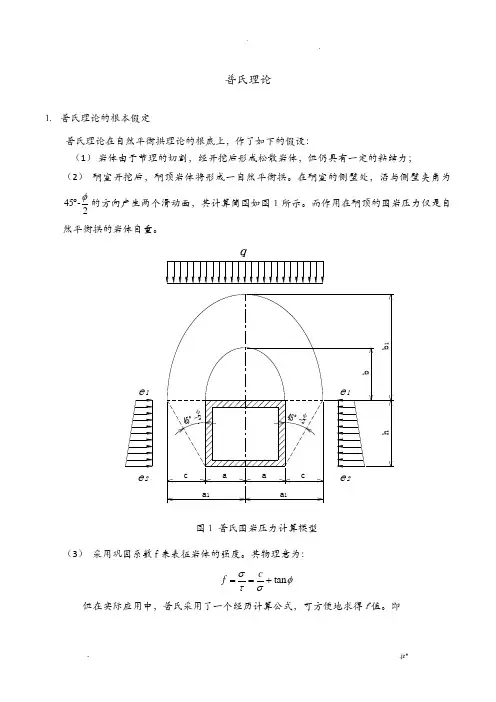
在硐室的侧壁处，沿与侧壁夹角为45-2φ︒的方向产生两个滑动面，其计算简图如图1所示。

而作用在硐顶的围岩压力仅是自然平衡拱的岩体自重。

1e 2图1 普氏围岩压力计算模型（3） 采用巩固系数f 来表征岩体的强度。

其物理意为：tan c f σφτσ==+但在实际应用中，普氏采用了一个经历计算公式，可方便地求得f 值。

即10c R f = 式中Rc ——单轴抗压强度〔MPa 〕。

f ——一个量纲为1的经历系数，在实际应用中，还得同时考虑岩体的完整性和地下水的影响。

（4） 形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2. 普氏理论的计算公式（1） 自然平衡拱拱轴线方程确实定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱岩体的自重。

先假设拱周线是一条二次曲线，如图2所示。

在拱轴线上任取一点M 〔x,y 〕，根据拱轴线不能承受拉力的条件，那么所有外力对M 点的弯矩应为零。

即202qx Ty -=〔a 〕 式中 q ——拱轴线上部岩体的自重所产生的均布荷载；T ——平衡拱拱顶截面的水平推力；x ，y ——分别为M 点的x ，y 轴坐标。

上述方程中有两个未知数，还需建立一个方程才能求得其解。

由静力平衡方程可知，上述方程中的水平推力T 与作用在拱脚的水平推xOT图2 自然平衡拱计算简图力T ＇数值相等，方向相反。

即T=T ＇由于拱脚很容易产生水平位移而改变整个拱的力分布，因此普氏认为拱脚的水平推力T ＇必须满足以下要求T ＇≤qa 1f 〔b 〕即作用在拱脚处的水平推力必须小于或者等于垂直反力所产生的最大摩擦力，以便保持拱脚的稳定。

此外，普氏为了平安，又将水平推力降低一半后，令T= qa 1f/2，代入〔a 〕式可得拱轴线方程为21x y a f= 显然，拱轴线方程是一条抛物线。

地基极限荷载是指地基土体完全发生剪切破坏时所承受的荷载，目前对于地基极限荷载的计算理论仅限于整体剪切破坏型式。

对于局部剪切破坏及刺入剪切破坏，尚无可靠的计算方法，通常是先按整体剪切破坏型式进行计算，再作某种修正。

极限荷载的求解有两类途径：一类是根据土体的极限平衡原理，另一类是根据模型试验。

先假定在极限荷载作用时土中滑动面的形状，然后根据滑动土体的静力平衡条件求解极限荷载。

这类方法又由于假设的滑动面形状不同，导出了多种形式的计算公式。

太沙基公式太沙基在1943年提出了确定条形浅基础的极限荷载公式。

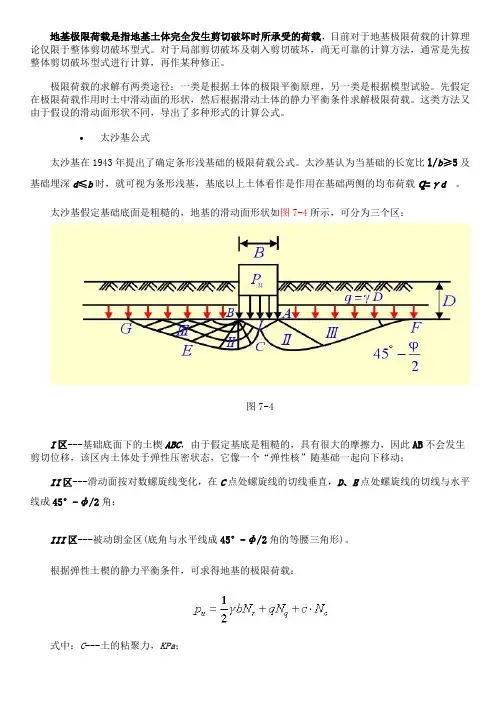
太沙基认为当基础的长宽比l/b≥5及基础埋深d≤b时，就可视为条形浅基，基底以上土体看作是作用在基础两侧的均布荷载q=γd。

太沙基假定基础底面是粗糙的，地基的滑动面形状如图7-4所示，可分为三个区：图7-4I区---基础底面下的土楔ABC，由于假定基底是粗糙的，具有很大的摩擦力，因此AB不会发生剪切位移，该区内土体处于弹性压密状态，它像一个“弹性核”随基础一起向下移动；II区---滑动面按对数螺旋线变化，在C点处螺旋线的切线垂直，D、E点处螺旋线的切线与水平线成45°-φ/2角；III区---被动朗金区(底角与水平线成45°-φ/2角的等腰三角形)。

根据弹性土楔的静力平衡条件，可求得地基的极限荷载：式中：C---土的粘聚力，KPa；q---基础两侧土压力q=γ0d，若地基土是均质，则基础两侧土压力q=γd；若地基土是非均质，则γ0是基底以上土的加权平均重度；d---基底埋深，m；b---基础宽度，m；N、N q、N c---无量纲承载力系数，可根据内摩擦角从表7-2查出。

r以上公式只适用于地基土整体剪切破坏情况，即地基土较密实，其P-S曲线有明显的转折点，破坏前沉降不大等情况。

对于松软土质，地基破坏是局部剪切破坏，沉降较大，其极限荷载较小。

太沙基建议采用较少的φ′，C′值代入公式计算极限荷载，即得：此时极限荷载公式为：式中N r′、N c′、N q′是相应于局部剪切破坏情况的承载力系数，根据降低后的摩擦角φ′查表7-2。

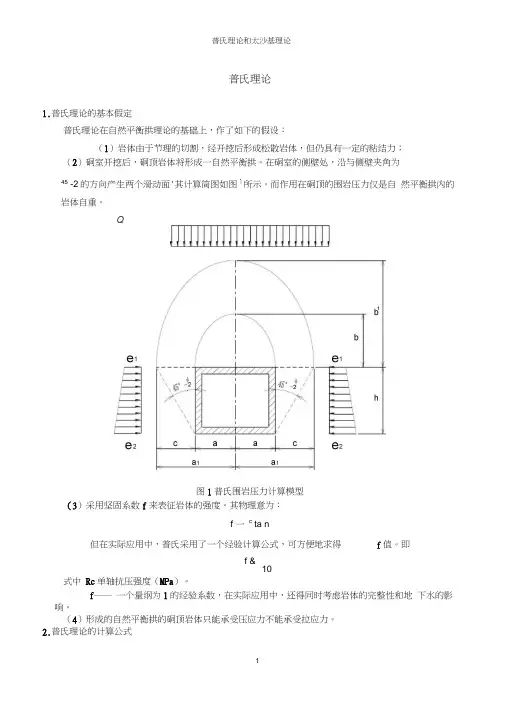
普氏理论1.普氏理论的基本假定普氏理论在自然平衡拱理论的基础上，作了如下的假设：（1）岩体由于节理的切割，经开挖后形成松散岩体，但仍具有一定的粘结力；（2）硐室开挖后，硐顶岩体将形成一自然平衡拱。

在硐室的侧壁处，沿与侧壁夹角为45 -2的方向产生两个滑动面'其计算简图如图1所示。

而作用在硐顶的围岩压力仅是自然平衡拱内的岩体自重。

Q图1普氏围岩压力计算模型（3）采用坚固系数f来表征岩体的强度。

其物理意为：f 一c ta n但在实际应用中，普氏采用了一个经验计算公式，可方便地求得f值。

即f &10式中Rc单轴抗压强度（MPa）。

f―― 一个量纲为1的经验系数，在实际应用中，还得同时考虑岩体的完整性和地下水的影响。

（4）形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2.普氏理论的计算公式(1)自然平衡拱拱轴线方程的确定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱内岩体的自重。

先假设拱周线是一条二次曲线，如图2所示。

在拱轴线上任取一点M( x,y)，根据拱轴线不能承受拉力的条件，则所有外力对M点的弯矩应为零。

即2Ty 坐0 ( a)2式中q――拱轴线上部岩体的自重所产生的均布荷载；T――平衡拱拱顶截面的水平推力；x，y ---- 分别为M点的x，y轴坐标。

上述方程中有两个未知数，还需建立一个方程才能求得其解。

由静力平衡方程可知，上述方程中的水平推力T与作用在拱脚的水平推qx O图2自然平衡拱计算简图力「数值相等，方向相反。

即T=T /由于拱脚很容易产生水平位移而改变整个拱的内力分布，因此普氏认为拱脚的水平推力T，必须满足下列要求T7< qd7(b)即作用在拱脚处的水平推力必须小于或者等于垂直反力所产生的最大摩擦力，以便保持拱脚的稳定。

此外，普氏为了安全，又将水平推力降低一半后，令T= qa i f/2，代入(a)式可得拱轴线方程为2xy df显然，拱轴线方程是一条抛物线。

问答题：
1.临塑荷载是塑性区发展深度是多少时的荷载？
2.中心受压基础，临界荷载是塑性区发展深度是
多少时的荷载？
3.偏心受压基础，临界荷载是塑性区发展深度是
多少时的荷载？

1212
临塑荷载与临界荷载-作业1
1.临塑荷载是塑性区发展最大深度为零时的荷载；
亦即地基即将发生塑性变形时的荷载。
2.中心受压基础，临界荷载是塑性区最大发展深
3.地基极限荷载的理论公式简介
太沙基公式
太沙基理论的Biblioteka 限承载力理论解1 = 1 + +
2
Nr、Nq、Nc均为承载力系数，均与有关，可
查太沙基公式的承载力系数曲线 ，见下页图
地基极限荷载的理论公式简介
太沙基公式的承载力系数曲线
局部剪切破坏时
地基极限承载力
1
2
= 1 ′ + ′ + ′
极限荷载
地基极限荷载的理论公式简介
太沙基公式
假定
底面粗糙，基底与土之间有较大
的摩擦力，能阻止基底土发生剪
切位移，基底以下土不会发生破
坏，处于弹性平衡状态；
基础两侧基底水平面以上土体可
以看做超载
Ⅰ区：弹性压密区(弹性核)
Ⅱ区：边界是对数螺线
Ⅲ区：被动朗肯区， 破裂面与水平面成45o- / 2
度zmax=b/4时的荷载。
3.偏心受压基础，临界荷载是塑性区最大发展深
度zmax=b/3时的荷载。
2
3
圆形基础
= 0.61 + 1.2 +
地基极限荷载的理论公式简介
太沙基公式的承载力系数曲线
方形基础

太沙基极限承载力公式
太沙基极限承载力公式是一种用于计算地基太沙基承载力的公式。

该公式基于史密斯和安德森（Smith and Anderson）于1952年提出的原始公式，经过多年的实验和改进，已经成为计算太沙基承载力的标准公式。

太沙基极限承载力公式的计算方法基于太沙基直径、太沙基长度、土壤强度参数和岩石强度参数等因素。

该公式的计算结果可以用于评估太沙基在不同地质和土壤条件下的承载力，并指导太沙基设计和施工。

太沙基极限承载力公式的基本形式为：
Qb = cNcAc + γDNqAq + 0.5γBfNγAg
其中，Qb表示太沙基的极限承载力；c、Nc、Ac表示土壤的可塑性指数、承载力增益系数和底面积；γ、D、Nq、Aq表示土壤的单位重量、太沙基直径、侧面土的修正系数和侧面积；Bf、Nγ、Ag表示太沙基底面上的摩擦系数、侧面土的修正系数和太沙基底面积。

太沙基极限承载力公式的计算需要通过实验和现场测量来确定土壤和太沙基的强度参数和几何参数。

同时，该公式只适用于特定的地质和土壤条件下的太沙基设计和施工，不能直接应用于其他地区和场合。

因此，在使用太沙基极限承载力公式时，需要结合实际情况进行综合考虑和分析，确保太沙基设计和施工的安全
和可靠性。

一、饱和土的渗流固结 二、太沙基一维固结理论
太沙基（K．Terzaghi，1925）一维固 结理论可用于求解一维有侧限应力状态下， 饱和粘性土地基受外荷载作用发生渗流固 结过程中任意时刻的土骨架及孔隙水的应 力分担量，如大面积均布荷载下薄压缩层 地基的渗流固结等。
1.基本假设
l）土是均质的、完全饱和的； 2）土粒和水是不可压缩的； 3）土层的压缩和土中水的渗流只沿竖 向发生，是单向（一维）的； 4）土中水的渗流服从达西定律，且土 的渗透系数k和压缩系数a在渗流过程 中保持不变； 5）外荷载是一次瞬时施加的。
饱和软粘土地基
沉降计算方法
初始沉降
固结沉降
次结沉降
次固结变形定义
次固结变形为主固结变形完成后，土体的变形在时
间上把主固结变形和次固结变形截然分开的意见在学术 界看法是不一致的。 将地基沉降分成三部分是从变形机理角度考虑，并 不是从时间角度划分的地基固结沉降和次固结沉降难以 在时间上分开。
由
Ut 1
8

2
e

2
4
Tv
0.5
得： 由
Tv 0.196
4cv t Tv 2 H
可得：
Tv H 2 t 181.6days 4cv
即 在181.6天内建筑物的固结沉降量为最终沉降量的一半。
试简述如何用固结理论求解下列两种课题的步骤：（1）已知历时求沉降量；（2） 估算达到某沉降量的历时。 答: (1) 已知历时求沉降量的步骤 a 估计该土层的最终沉降量S； b 计算该土层的竖向固结系数 c 计算竖向固结时间因数 Tv d 应用公式 U z 1
（2）根据达西定律：
q ki k
h z

太沙基方形基础极限承载力公式说到“太沙基方形基础极限承载力公式”，别急，别害怕，不是要给你讲什么枯燥的数学公式或是那些让人头大的理论，今天咱们就是聊聊这玩意儿，怎么回事，为什么它这么重要，咱们怎么能用它来做点实际的事情。

先说说这“太沙基方形基础”，大家都知道，建筑物在土壤上的“基础”就像是咱们站在地上的脚一样，得有个稳稳当当的支撑，才能让整个建筑物不发生倾斜或者沉降，对吧？说白了，就是得让建筑物不掉下来。

这时候，土壤就成了最关键的角色。

说到这里，大家肯定有个疑问：“那啥时候土壤会出问题？它究竟是怎么‘承受’的？”这就是我们要讨论的“极限承载力”。

极限承载力，简单来说，就是土壤能够承受的最大压力。

再往通俗点说，就是当你往土地上压，它能压到什么程度，不会让整个土地“崩溃”掉，或者说变成“软绵绵的糯米团”那种。

但这玩意儿也不是随便就能估算的，不是你随便扔个石头就知道它有多重，得考虑很多因素。

这时候，就要用到所谓的“极限承载力公式”了。

嘿，听着是不是有点高大上？其实就是一种数学公式，能帮助我们计算出来，假如土壤承受的压力达到某个极限值时，它会发生什么变化，能支撑多重的负荷。

你想啊，要是咱们不算清楚，万一这个基础设计出了问题，建筑物突然“压塌”了，后果可想而知。

所以，这个公式其实就是帮我们做个“保险”，确保土壤能撑得住，建筑物能稳稳当当地立在地上。

至于说方形基础，那是因为在实际建设中，很多建筑物的基础设计都采取了方形的设计。

你看，圆形、椭圆形都可以，但方形相对来说稳定性好，施工也简单，容易计算。

所以，一般来说，方形基础最常见，也最符合咱们的需求。

好了，扯这么多，总结下来，其实就俩字：“稳住”。

讲到这里，可能有的小伙伴会想：这些理论跟我有啥关系，能吃吗？不能！但这正是工程建设中的基础知识，要知道，咱们每次盖楼、修桥、做高速公路、建地铁的时候，背后都离不开这些看似抽象的公式和理论。

你站在一栋大楼下面，抬头看着那座雄伟的建筑，可能没想到的是，地下的基础可能已经计算了千百遍，确保它不会因为一个小小的设计错误就发生倾斜或倒塌。

泰沙基理论与公式太沙基理论是从应力传递原理出发推导竖向围岩压力的。

如图1所示，支护结构受到上覆地压作用时，支护结构发生挠曲变形，随之引起地块地移动。

当围岩的内摩擦角为时，滑移面从隧道底面以的角度倾斜，到硐顶后以适当的曲线AE和BI到达地表面。

但实际上推算AE和BI曲线是不容易的，即使推算出来，以后的计算也变得很复杂，故近似地假定为AD、BC两条垂直线。

此时，设从地表面到拱顶的滑动地块的宽度为2a1，其值等于：（1）式中 a——硐室半宽；H——开挖高度。

假定硐室顶壁衬砌顶部AB两端出现一直延伸到地表面的竖向破裂面AD及BC。

在ABCD所圈出的散体中，切取厚度为dz的薄层单元为分析对象。

该薄层单元受力情况如图1所示，共受以下五种力的作用：（1）单元体自重（2）（2）作用于单元体上表面的竖直向下的上覆岩体压力（3）（3）作用于单元体下表面的竖直向上的下伏岩体托力（4）（4）作用于单元体侧面的竖直向上的侧向围岩摩擦力（5）（5）作用于单元体侧面的水平方向的侧向围岩压力（6）式中 a1——开挖半宽；γ——岩体容重；σv——竖向初始地应力；k0——侧压力系数；dz——薄层单元体厚度；τf——岩体抗剪强度；初始水平地应力为（7）则岩体抗剪强度为（8）式中 c——岩体内聚力；——岩体内摩擦角。

将式（8）带入式（5）得（9）薄层单元体在竖向的平衡条件为(10)将式（2）、式（3）、式（4）及式（9）代入式（10）得（11）整理式（11）得(12)由式（12）解得（13）边界条件：当z=0时， =p0(地表面荷载)。

将该边界条件代入式（13）得(14)将（14）代入式（13）得：（15）式中 z——薄层单元体埋深。

将z=H代入式（15）时，可以得到硐室顶部的竖向围岩压力q为：（16）设为相对埋深系数，代入式（16）得：（17）式(17)对于深埋硐室及浅埋硐室均适用。

将代人式（17），可以得到埋深很大的硐室顶部竖向围岩压力q为：（18）由式(18)可以看出，对于埋深很大的深埋硐室来说，地表面的荷载P0对硐室顶部竖向围岩压力q已不产生影响。

（普朗特尔极限承载力公式）1.地基土是均匀，各向同性的无重量介质，即认为基底下土的容重等于零，而只具有c,φ的材料。

2.基础底面光滑，即基础底面与土之间无摩擦力存在。

因此，水平面为大主应力面，竖直面为小主应力面。

3.当地基处于极限（或塑性）平衡状态时，将出现连续的滑动面，其滑动区域即将由朗肯主动区Ⅰ，径向剪切区Ⅱ和朗肯被动区Ⅲ所组成，如图(a)所示。

其中滑动区Ⅰ的边界(或)为直线并与水平面成（）角；滑动区Ⅱ的边界(或)为对数螺旋曲线，其曲线方程为，为起始矢径()；滑动区Ⅲ的边界(或)为直线并与水平面成（）角。

4.当基础有埋置深度D时，将基础底面以上的两侧土体用当量均布超载q等于来代替，如图（b)所示1.基础底面粗糙，即它与土之间有摩擦力存在。

因此，虽然当地基达到破坏并出现连续滑动面时，其基底下有一部分将随着基础一起移动而处于弹性平衡状态，该部分土体称为弹性楔体，如图(a)中的aba所示。

弹性楔体的边界ab为滑动面的一部分，它与水平面的夹角为，角的具体数值与基底的粗糙程度有关。

当把基底看作完全粗糙时，由于弹性楔体内的土只有与基础一起竖直向下移动的可能性，这种移动必然要求通过b点的滑动面bc的开始段应是一根竖直线。

因ab也是滑动面，而在塑性区域内过每一点的一对滑动面彼此应交成()角，所以，由几何关系可知，等于，如图(b)所示；当把基底看作完全光滑时，则等于，如图(c)所示,一般情况，介于与之间。

2.当把基底看作完全粗糙时，则滑动区域由径向剪切区Ⅱ和朗肯被动区Ⅲ所组成，如图(b)所示，其中滑动区Ⅱ的边界bc为对数螺旋曲线。

朗肯被动区Ⅲ的边界cd为直线，它与水平面成角。

3.当基础埋置深度为D时，则基底以上两侧的土体用当量均布超载q（等于）来代替。

太沙基计算原理：dhtg k Cdh bd bdh v v ϕσσγ2222++=简化后写为 b tg k b C dh d v v ϕσγσ--= 并由边界条件h=0处，v σ=q 及h=h c 处，v σ=P ，解方程，即可获得隧洞顶部的围岩压力P 为⎪⎭⎫ ⎝⎛-+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛---=b khtg q b khtg ktg C b P ϕϕϕγexp exp 1 （2-119） ()⎪⎭⎫ ⎝⎛--+=245ϕ tg h h b b c t 式中：γ为容重；k 为静止侧压力系数，太沙基取k=1;q 为地面荷载。

式（2-119）表明，隧洞埋深较浅时，松动压力与埋深有关；埋深较大时，公式中指数项趋于零，即ϕγktg C b P -= 而与埋深无关。

普氏理论：这一计算方法是将破裂区内的岩体自重作为隧洞支护上的荷载。

为了确定破裂区的范围，必须首先对破裂区的边界线做出假定，如认为是抛物线、半椭圆形等，此外还有采用弹塑性区的分界面作为破裂区的边界线。

普氏压力拱理论、康姆瑞尔（O.Kommerell ）的岩体破碎理论，以及卡柯弹塑性理论都属于这一类计算方法。

其中以普氏压力拱理论在我国应用最广。

普氏认为，隧洞开挖后，顶部岩体失去稳定，产生坍塌，并形成自然拱。

随之，隧洞两侧由于应力集中而逐渐破坏。

因此，顶部坍塌进一步扩大形成塌落拱。

如图所示，如果隧洞开挖后及时支护，按照挡土墙原理，侧面岩石的破裂面与垂直轴的夹角为⎪⎭⎫ ⎝⎛-245ϕ ，顶部的破坏则介于自然拱和塌落拱之间，而破坏拱以内的岩石自重即为作用在隧洞支护上的围岩压力，因而普氏破坏拱又称压力拱。

普氏假定压力拱形状为二次抛物线形，压力拱高*h 按经验确定，它取决与隧洞跨度和岩石性质。

普氏采用下式确定压力拱高*h ftg h b f b h t t ⎪⎭⎫ ⎝⎛-+==245**ϕ 式中：f 为岩石坚固性系数，又称普氏系数。

普氏根据不同的岩性给出了相应的普氏系数，或按10c R （R c 为岩石抗压强度，MPa ）确定普氏系数。

普氏理论和太沙基理论普氏理论1.普氏理论的基本假设普氏理论在自然平衡拱理论的基础上，作了如下的假设：（1）由于节理的切割，开挖后岩体形成松散岩体，但仍有一定的粘结力；（2）硐室开挖后，硐顶岩体将形成一自然平衡拱。

在硐室的侧壁处，沿与侧壁夹角为? 45?- 在方向上生成两个滑动面，计算图如图1所示。

作用在隧道顶部的围岩压力仅为自身压力2然平衡拱内的岩体自重。

e1φ2φ2e1he2ca1aaa1ce2图1普氏围岩压力计算模型（3）坚固系数f用于表征岩体的强度。

它的物理意义是：?cf???tan???然而，在实际应用中，Proctor采用了一个经验计算公式，可以很容易地获得F的值rf?c式中RC——单轴抗压强度（MPA）。

f――一个量纲为1的经验系数，在实际应用中，还得同时考虑岩体的完整性和地水的影响。

（4）形成的自然平衡拱的硐顶岩体只能承受压应力不能承受拉应力。

2.普氏理论的计算公式一bb1（1）自然平衡拱拱轴线方程的确定为了求得硐顶的围岩压力，首先必须确定自然平衡拱拱轴线方程的表达式，然后求出硐顶到拱轴线的距离，以计算平衡拱内岩体的自重。

先假设拱周线是一条二次曲线，如图2所示。

在拱轴线上任取一点m（x,y），根据拱轴线不能承受拉力的条件，则所有外力对m点的弯矩应为零。

即qx2ty？？0（a）2式中q――拱轴线上部岩体的自重所产生的均布荷载；t――平衡拱拱顶截面的水平推力；x、 Y——点M的x轴和Y轴的坐标。

上述方程中有两个未知数，还需建立一个方程才能求得其解。

由静力平衡方程可知，上述方程中的水平推力t与作用在拱脚的水平推xyomxtb1t'a1φqa1y图2自然平衡拱计算简图力t’的值相等，方向相反。

即t=t＇由于拱脚容易产生水平位移并改变整个拱的内力分布，Proctor认为拱脚的水平推力t’必须满足以下要求t＇≤qa1f（b）也就是说，作用在拱脚上的水平推力必须小于或等于垂直反作用力产生的最大摩擦力，以保持拱脚的稳定性。

太沙基承载系数表(可以直接使用，可编辑实用优秀文档，欢迎下载）图7-4I区---基础底面下的土楔ABC，由于假定基底是粗糙的，具有很大的摩擦力，因此AB不会发生剪切位移区内土体处于弹性压密状态，它像一个“弹性核”随基础一起向下移动；II区---滑动面按对数螺旋线变化，在C点处螺旋线的切线垂直，D、E点处螺旋线的切线与水平线成45°角；III区---被动朗金区(底角与水平线成45°-φ/2角的等腰三角形)。

根据弹性土楔的静力平衡条件，可求得地基的极限荷载：式中：C---土的粘聚力，KPa；q---基础两侧土压力q=γ0d，若地基土是均质，则基础两侧土压力q=γd；若地基土是非均质，则γ0以上土的加权平均重度；d---基底埋深，m；b---基础宽度，m；N、N q、N c---无量纲承载力系数，可根据内摩擦角从表7-2查出。

r以上公式只适用于地基土整体剪切破坏情况，即地基土较密实，其P-S曲线有明显的转折点，破坏前沉等情况。

对于松软土质，地基破坏是局部剪切破坏，沉降较大，其极限荷载较小。

太沙基建议采用较少的φ′值代入公式计算极限荷载，即得：此时极限荷载公式为：式中N r′、N c′、N q′是相应于局部剪切破坏情况的承载力系数，根据降低后的摩擦角φ′查表7-2表7-2 太沙基公式承载力系数表φ0°5°10°15°20°25°30°35°40°45°N r0 0.51 1.20 1.80 4.0 11.0 21.8 45.4 125 326 N q 1.0 1.64 2.69 4.45 7.42 12.7 22.5 41.4 81.3 173 N c 5.71 7.32 9.58 12.9 17.6 25.1 37.2 57.7 95.7 172上述公式只适用于条形基础，对方形和圆形基础，太沙基建议按下列修正公式计算地基极限荷载：方形基础：整体剪切破坏：局部剪切破坏：圆形基础：整体剪切破坏：局部剪切破坏：式中r为圆形基础的半径，其余符号同前。