小学二年级奥数第12讲 画图解题(含答案)

二、探索发现授课［40分］［一］例题1：［13分］欧拉、阿派、卡尔三个人看比赛,三个人支持的队伍是红队、黄队和蓝队。

请问,他们三人分别支持什么队伍？［］［］［］师：我们在推理的过程中也是考验我们一些常识性的知识的时候,比如妈妈问你,作业做完了没有,你回答说,还有一题没有做,那你是做完了还是没做完？生：没有。

师：像这样的问题,就算没有直接告诉我们,我们也能够得到自己想要的信息, 这个思考过程就叫做推理。

接下来我们看看下面的这个问题,你能不能通过推理找到想要的结果呢？谁来读一读？生：［读题］［请三位同学扮演欧拉、阿派进行对话］师：这里最容易找到的信息是哪一句话？生：欧拉说的“我支持的队伍是大海的颜色。

”大海的颜色是蓝色,所以欧拉支持的是蓝队。

师：找得非常准确,开了一个好头,那么现在还有哪两个队不知道是谁支持的？生：红队和黄队！师：你们推出来了没有？生：推出来了,阿派支持的是黄队,卡尔支持的是红队。

师：说一说你是根据什么推出来的？生：阿派说他支持的不是红队,只有两个队,那么他支持的只能是黄队。

黄队有阿派支持,那么剩下的红队就一定是卡尔支持的。

师：你们的结果是不是一样的？生：是！师：前面是根据我们的常识推出来的,我们知道大海的颜色是蓝色,那欧拉支持的就是蓝队。

第二个我们用排除的方法,后面两个人,不是支持红队就是黄队,正好阿派说他支持的不是红队,那么就只有是黄队了。

你们除了这个思考方式,还有其他的方式吗？生：还可以先推出欧拉支持的是蓝队,阿派不支持红队,那么支持红队的就是卡尔,剩下的黄队就是阿派支持的。

师：非常棒！别看这么一个小小的推理题,里面也有多种思考方向,接下来咱们就小小地试一下。

做一做练习。

板书：欧拉：蓝队；阿派：黄队；卡尔：红队。

练习1：［6分］三个人考试成绩分别是96分、98分、100分。

［］［］［］分析：这里的分数只有3个,分别是96分,98分和100分,人也只有3个人,那么这里一定是一一对应的。

二年级奥数-画图法(总11页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第10课时用画图法解题一、教学目标1.培养学生根据题意画图的能力，使其初步掌握这种方法。

2.教会学生画图的方法，阿凡提和巴依老爷是邻居.阿凡提家有6只羊，巴依家有12只羊.一天，巴依把自己家的羊卖了6只，又偷来阿凡提家的6只羊，和自家剩下的6只羊混在一起，关在自家羊圈里，每边关3只(如图).但聪明的阿凡提把羊重新排了一下，牵回了被巴依偷的6只羊，而且每边仍是3只.你知道阿凡提是怎样排的羊吗本节课主要内容：我们在解决很多应用题的时候都需要通过画图来解决，学生根据题意画图的能力，也决定了他的解题能力，这种能力需要从小培养.那么在本节课中我们将通过一些典型例题来引导孩子学习画图的方法,让学生会用画直观图的方法来解决鸡兔同笼和排队问题.会用画线段图的方法来解决简单的倍数问题.【教学思路】首先老师要引导学生读故事，然后画出如左下图的简易图，开始的时候是12只羊，每边3只，中间是房子所以不放.阿凡提把自己家的6只羊都牵走了，这样就只剩下6只羊来重新排列，而且还必须每边3只.具体排法如右下图：在数学的海洋中，有时解决一些问题你是否发现只要我们多动手，动手摆一摆、动手画出直观图，就可以很轻松的解决问题呢！画图的方法有很多，如画线段图、画直观图等，究竟这些方法应该怎样应用呢？下面就让我们通过一些数学问题来体会画图法的妙用吧！很多数学问题，都可以用画图法小朋友们，我们所学习的排队问题一般可以通过画图来解决，我们不妨来试一试.二年级同学外出参观，二(1)班34人排成一行，从左向右数，小雪是第8个，从右向左数，小芹是第9个，那么从小雪数到小芹一共有多少个同学【教学思路】排队问题对于低年级孩子理解起来比较抽象，我们可以通过画图来引导学生理解.方法一：从图中看出，从左数小雪排第8个，也就是小雪的左边有7个人，从右数小芹排第9个，也就是小芹的右边有8个人，这样从小雪开始数到小芹只需要从总人数中把小雪左边的7个人和小芹右边的8个人减掉就可以了，列式：34-（8-1）-（9-1）=19（人）方法二：从图中看出，从左数小雪排在第8个，也就是从左边到小雪有8个人，从右数小芹排第9个，也就是从右到小芹有9个人，其余的人就排在小雪和小芹中间.中间有34-8-9=17（人），这样加上小雪和小芹一共有19人.列式：34-8-9=17（人）；17+2=19（人）答：从小雪数到小芹一共有19个同学.巩固练习在一次数学竞赛的颁奖大会上，同学们排成一队上台领奖，从排头数起李阳是第22个；从排尾数起，何平是第24个.已知李阳的前一个是何平.问一共有多少同学上台领奖【教学思路】右图可见，从排头数起的22人，把何平和李阳数了一次，由排尾数起的24人，又把李阳和何平数了一次，这样，把两人都多数了一次，所以，在计算总人数时，应该减去多数的2人.列式：22+24-2=44（人），这队共有同学44人.对于排队问题，我们在春季将进一步的来学习，到时候同学们就可以用画图的方法大显身手了.现在我们再来研究另一种有趣的问题——鸡兔同笼问题，这个问题一定要通过画图才能更好的理解.王大妈去市场上买回来了一些鸡和兔，她把鸡、兔关在同一个笼子里，数了数,共有10个头，26条腿，你知道王大妈买回来了几只鸡几只兔【教学思路】因为这道题只跟动物的头和腿有关，那么可以画出直观图进行分析.我们可以用“〇”表示头，画十个“〇”；用“|”表示一条腿，先把它们全部看作是腿较少.的动物，也就是全部画成鸡少画了26-20=6条腿，由于一只兔子比一只鸡多两条腿，6÷2=3（只），所以我们应该在三只鸡的图上再分别加上两条腿，使它们成为兔子，则鸡有10-.3=7（只）巩固练习一只蛐蛐6条腿，一只蜘蛛8条腿.有蛐蛐和蜘蛛共10只，共68条腿，蛐蛐和蜘蛛各有多少只?我们仍然可以用图来帮忙，“〇”表示头，但由于蛐蛐和蜘蛛的腿比较多，画“|”不方便，我们就用数字表示腿的条数.写在头的下面，先把它们看成是腿较少的动物——蛐蛐，然后再看差了几条腿，需要在几只蜘蛛上各添上2只，就达到68条腿，问题【教学思路】从图中可以看出：十只蛐蛐一共有六十条腿，比已知条件少了68-60=8（条）腿，而一只蜘蛛比一只蛐蛐多两条腿，8÷2=4（只）.只要在四只蛐蛐的图上再各添两条腿，使它们成为蜘蛛的表示图就行了.所以共有4只蜘蛛，10-4=6（只）蛐蛐.一辆自行车有2个轮子，一辆三轮车有3个轮子.车棚里放着自行车和三轮车共8辆，共20个轮子.自行车、三轮车各有多少辆【教学思路】通过画图进行分析，如果都堪称自行车，那么一共是2×8=16（个）轮子，还差20-16=4（个）轮子，自行车比三轮车少一个轮子，所以就有4辆三轮车.还剩下8-4=4（辆）就是自行车.一共有4辆三轮车和4辆自行车.还有一些应用题，我们不容易直接分出他们的数量关系，这时我们可以通过画线段图的方法来解决问题，画线段图可是我们解决应用题的法宝哦!奥数网图书采购员去西单图书大厦买《奥数课本》一书，他的钱若买4本还剩2元；若买5本，就差7元．问采购员带了有多少钱?【教学思路】这道题用画图法显示更容易分析.依题意画出线段图，由图可见一本的价钱是：2+7=9（元）所以采购员有的钱是9×4+2=38(元) 或9×5-7＝38(元).一筐鲜鱼，连筐共重56千克．先卖出鲜鱼的一半，再卖出剩下的一半，这时连筐还重17千克．原来这筐鲜鱼重多少千克【教学思路】由图可以看出总重减去最后剩下的(包括筐重和鱼)等于第一次和第二次卖出的鲜鱼总数．又知第一次卖出的是第二次卖出的2倍，即两次卖出的鲜鱼总数是第二次卖出的3倍，即得第二次卖出鱼的总量为(56－17)÷3＝13千克．原来鲜鱼总数为13×4＝52千克．小军、小方和小雄共有12本小人书，小军比小方多2本，小方比小雄多2本，问他们三人各几本?【教学思路】通过“小军比小方多2本，小方比小雄多2本”可知：小雄的小人书最少，然后是小方的，最后小军的小人书最多，这样我们可以画出线段图.这道题的解答方法很多.方法一：把小军多的2本，补在小雄少的位置，这样三人的小人书就跟小方一样多.我们可以先求出小方的本数：12÷3=4（本）；小军：4+2=6（本）；小雄：4-2=2（本）.方法二：采用添加差线段的方法可得：(12+2×3)÷3＝6(本)(小军)；6－2＝4(本)(小方)；4－2＝2(本)(小雄)；方法三：同样也可采用去掉差线段的方法得： (12－2×3)÷3＝2(本)(小雄)； 2+2＝4(本)(小方)； 4+2＝6(本)(小军)．【教学思路】绳子的总厂不变，根据题意我们可画出线段图：小秋第二次把绳子对折量，井外留1米长的双股绳相当实际绳长2米，比第一次单股绳测时，井外少了15－2＝13(米)，因为这段绳放到井里去了，所以得出井深为13米．附加题（老师可根据自己的课堂进度灵活处理讲义内容，附加题仅供老师参考使用.）拓展与提高小秋用一根绳子测量一口枯井的深．他把绳子放入井里，当绳子到达井底后，井外还留有15米；小秋又把这根绳子对折后再放入井里，井外还留有1米．请问，这口枯井有多少米深?小初、小美、小英三个人分糖块．小美比小英多3块，小初比小美多2块．已知糖块总数是50块，那么每人各分到多少块【教学思路】依题意画图，可以先画小英，见上图中①，再画小美，它比小英多3块，见上图中②，接着再画小初，它又比小美多2块，见上图中③，至此，图已画完，下面借助此图进行分析推理．由图可见，小初比小英多3+2＝5块，由图还可以看出，50－(3+5)＝42(块)就是小英糖数的3倍，所以小英的一份是：42÷3＝14(块)；由此可求出小美的一份是14+3＝17(块)；小初的一份是17+2＝19(块)．小玲家养了46只鸭子，24只鸡，养的鸡和鹅的总只数比养的鸭多5只.小玲家养了多少只鹅?【教学思路】将已知条件表示为上图：表示为算式是：24+?=46+5.由此可求得养鹅(46+5)-24=27(只).父亲今年40岁，小丽10岁．问几年以后父亲年龄是小丽年龄的2倍【教学思路】这道题我们用画格子的方法，学生更直观一些.先画阴影部分，小丽(10岁)占1格，父亲(40岁)占4格，年龄差(40－10=30(岁))是3格，再画图表示二人年龄的增长，注意应从上往下画．不难得出当二人年龄各增加2格时，即20年后(父亲是6格，小丽是3格)父亲年龄是小丽年龄的2倍．个小朋友排队，从前往后数红红站在第8个，从后往前数明明站在第8个，红红和明明之间有几个小朋友？【答案】20-8-8=4个，红红和明明之间有4个小朋友.2.鸡兔同笼共有14个头，38条腿，有几只鸡几只兔【答案】有5只兔子和9只鸡.3.蛐蛐和蜘蛛共8只，腿54条，蛐蛐和蜘蛛各几只？【答案】有3只蜘蛛和5只蛐蛐.4.王强和李明都想买一本《趣味数学》，但王强的钱少2元5角，李明的钱少3元1角．如果两个人的钱合在一起就刚够买这本书．问一本《趣味数学》多少钱王强和李明各有多少钱【答案】一本书的书价是： 2元5角+3元1角＝5元6角．王强有3元1角，李明有2元5角．5. 玻璃瓶里装着一些水，把水加到原来的2倍时，和瓶一起称重5千克；把水加到原来的4倍时，再称一称重为9千克，问原来水有多少千克【答案】由图可见，线段③－线段②＝2倍小线段，即一条小线段表示(9－5)÷2＝2(千克)，即原来瓶中水重是2千克．狗熊卖瓜一天，狗熊艾伦推着一辆车，沿街叫卖着：“卖瓜啰，又甜又脆的西瓜，甜滋滋的葡萄……”听到叫卖声，狐狸麦思跑了过来：“这鬼天气可真热啊，熊大哥，你这西瓜怎么卖啊？”“便宜着呢，5元一个.”艾伦说.“那就给我拿2个吧.”麦思接过递过来的西瓜，突然他一拍脑袋说：“瞧我这记性，我儿子是让我来买葡萄的，怎么买也西瓜呀.熊大哥，你这葡萄怎么卖啊？”“2元一串，包甜.”“这样吧，我拿这2个西瓜换5串葡萄行不？反正都是10元钱.”麦思说.艾伦想了想爽快地说：“没问题.”说着接过2个西瓜，换了5串葡萄给麦思.麦思拿着5串葡萄刚要转身离去，被艾伦叫住了：“哎，狐狸老弟，你记性可真够差的，还没付钱呢.”麦思一愣，疑惑地说：“熊大哥，我看你搞错了吧！我是用2个西瓜换的这5串葡萄啊，你怎么能再向我要钱呢？”听麦思这么一说，艾伦急了：“可这西瓜的钱你并没有付啊？”麦思的脸一沉说：“咦奇怪了，有你这么做生意的吗我把西瓜不是还给你了吗怎么还问我要西瓜的钱啊！”这下艾伦给弄糊涂了：“你的确没有吃我的西瓜，当然就不用付西瓜的钱，可你手上拎的那5串葡萄是我的，你得付葡萄的钱呀？”“我不是跟你说了吗这葡萄是我用西瓜换的呀这葡萄的钱你就更不应该收了呀.”“对！对！对！是我搞错了，对不起啊，欢迎下次再来买.”艾伦赔着笑脸说.看到这儿，聪明的小朋友，你们说说这钱究竟该不该付呢？。

第一讲速算与巧算习题1.计算：18+28+72 28+44+62+562.计算：100-68= 100-87= 1000-369= 500-47=3、计算：67+98 261-1974.计算：72-39+28 382-60+595.计算：99+98+97+96+95 * 9+99+9996.计算：436-（36+57）579-83-177.计算：1+2+3+4+3+2+1= 1+2+3+4+5+1+2+3+4+5+6=8.计算：5+6+7+8+9 1+4+7+10+13+16提高班第一讲速算与巧算习题1.计算：18+28+72 28+44+62+56-202.计算：100-68= 1000-587= 1000-69= 500-47=3、计算：67+98 261-1974.计算：72-39+28 382-60+595.计算：99+98+97+96+95 9+99+9996.计算：436-（136+157）579-83-177.计算：1+2+3+4+3+2+1= 1+2+3+4+5+1+2+3+4+5+6=8.计算：5+6+7+8+9 1+4+7+10+13+16基础班第二讲图形计数习题1．数一数，图4－１中共有多少条线段?2．数一数，图中有多少个三角形?3．图中有多少个正方形?4．数一数，图形中有几个长方形?5.数一数，下图中有多少个三角形？多少个正方形？*6.数一数，下图中共有多少条线段?有多少个三角形?*7.数一数，下图中共有多少个小于180°角?*8.数一数，下图中共有多少个三角形？习题答案1. 10条线段2. 5个6个6个5个12个3. 5个17个4. 7个（4+3+2+1）×（3+2+1）=60（个）5. 6个三角形7个正方形6. 30条线段10个三角形7. 30个小于180°角10+3+6=19（个）9.提高班第二讲图形计数习题1．数一数，图4－１中共有多少条线段?*2．数一数，图4—2中共有多少条线段?3．数一数，图中有多少个三角形?*4.***5．图中有多少个正方形?6．数一数，图形中有几个长方形?7.数一数，图中共有几个三角形?几个正方形?8.数一数，下图中共有多少条线段?**有多少个三角形?9.数一数，下图各图中各有多少个三角形?*10.数一数，下图中有多少个小于180°角?习题答案1.10条线段2.14条线段3.5个6个6个5个4.12个12个5.5个17个6.7个（4+3+2+1）×（3+2+1）=60（个）7. 6个三角形7个正方形8. 30条线段10个三角形9. 19个三角形10. 30个小于180°角秋季班第三讲基础班1．把一根粗细均匀的木头锯成6段，每锯一次需要3分钟，一共需要多少分钟？2．把一根粗细均匀的木头锯成5段需要20分钟，每锯一次要用多少分钟？3．一根木料长10米，要把它锯成一些2米长的小段，每锯一次要用4分钟，共要用多少分钟？4.公园的一条林荫大道长300米，在它的一侧每隔30米放一个垃圾桶，需多少个垃圾桶？5.学校有一条长60米的走道，计划在道路两旁栽树。

一、计算题。

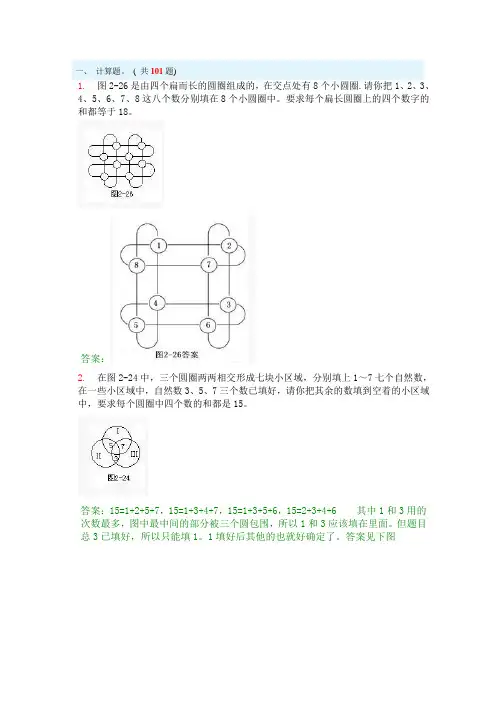
( 共101题)1.图2-26是由四个扁而长的圆圈组成的，在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。

要求每个扁长圆圈上的四个数字的和都等于18。

答案：2.在图2-24中，三个圆圈两两相交形成七块小区域，分别填上1～7七个自然数，在一些小区域中，自然数3、5、7三个数已填好，请你把其余的数填到空着的小区域中，要求每个圆圈中四个数的和都是15。

答案：15=1+2+5+7，15=1+3+4+7，15=1+3+5+6，15=2+3+4+6 其中1和3用的次数最多，图中最中间的部分被三个圆包围，所以1和3应该填在里面。

但题目总3已填好，所以只能填1。

1填好后其他的也就好确定了。

答案见下图3.图2-23中有三个大圆，在大圆的交点上有六个小圆圈。

请你把1、2、3、4、5、6六个数分别填在六个小圆圈里，要求每个大圆上的四个小圆圈中的数之和都是14。

答案：案把14拆成4个自然数的和，如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。

先把一个数填入，然后试一下确定其他数的位置。

答案如下图4.将2、4、6、8、10、12、14、16、18填在下面图表，使每一横行、竖行、斜行的三个数相加的和都相等。

答案：案九宫格填九数的方法，确定中间是10最关键了，然后我们对这些数加和除以3，就有了相等的和应该是30，图形如下(有很多种，但是中间那个肯定是10)5.仔细观察下面的图形，找出变化规律，猜猜在第3组的右框空白格内填一个什么样的图?答案：6.请看下图，共有多少个正方形?答案：30 个正方形。

小结小方格16 个，4 个小方格为一个正方形共 9 个，9 个小方格为一个正方形共 4 个，最大的(16 个小方格)是 1 个。

16+9+4+1=30(个)共计 30 个正方形。

7.仔细观察这些图案可以发现，他们是按照下面这5个图案为一组，循环往复排列的，请问第52个图形是什么?答案：8.把上面一排的立体图形剪开，可以剪成下面哪种图形的样子?动手试一试。

第一讲速算与巧算习题1。

计算:18+28+72 28+44+62+562。

计算：100—68= 100-87= 1000—369= 500-47=3、计算：67+98 261—1974.计算：72-39+28 382—60+595。

计算:99+98+97+96+95 * 9+99+9996。

计算：436—（36+57) 579—83-177.计算：1+2+3+4+3+2+1= 1+2+3+4+5+1+2+3+4+5+6= 8。

计算：5+6+7+8+9 1+4+7+10+13+16提高班第一讲速算与巧算习题1.计算：18+28+72 28+44+62+56—202。

计算:100-68= 1000-587= 1000—69= 500-47= 3、计算:67+98 261—1974。

计算：72—39+28 382-60+595。

计算：99+98+97+96+95 9+99+9996.计算：436-（136+157）579—83-177.计算：1+2+3+4+3+2+1= 1+2+3+4+5+1+2+3+4+5+6= 8。

计算:5+6+7+8+9 1+4+7+10+13+16基础班第二讲图形计数习题1．数一数，图4－１中共有多少条线段?2．数一数，图中有多少个三角形?3．图中有多少个正方形？4．数一数，图形中有几个长方形？5。

数一数,下图中有多少个三角形？多少个正方形？＊6。

数一数，下图中共有多少条线段?有多少个三角形？*7.数一数,下图中共有多少个小于180°角？＊8。

数一数，下图中共有多少个三角形？习题答案1。

10条线段2. 5个6个6个5个12个3. 5个17个4. 7个(4+3+2+1)×（3+2+1）=60(个）5。

6个三角形7个正方形6。

30条线段10个三角形7. 30个小于180°角10+3+6=19（个）9.提高班第二讲图形计数习题1．数一数，图4－１中共有多少条线段？＊2．数一数,图4—2中共有多少条线段？3．数一数，图中有多少个三角形？＊4.*＊*5．图中有多少个正方形？6．数一数，图形中有几个长方形？7。

二年级奥数教程第12讲：画图法解应用题在解应用题时，特别是一些技巧性比较大的题，如果不认真思考，是很容易做错的．这时你不妨先画一画图，用图来表示题目中的条件，能方便我们理解题意，正确思考解答．例1 16 名同学排成一队，在解应用题时，特别是一些技巧性比较大的题，如果不认真思考，是很容易做错的．这时你不妨先画一画图，用图来表示题目中的条件，能方便我们理解题意，正确思考解答．例1 16名同学排成一队，从前往后数，小小排在第7个，从后往前数，他排在第几个?解我们用下图来表示：通过画图，我们可以发现：从前往后数，小小排在第7个，也就是从最前面到小小共有7个人．由于一共有16个人，所以小小后面还有16-7=9(人)．从后面往前数的话，数到小小应该是第10人，即16-7+l=10(人)．答：从后往前数，小小排在第10个．随堂练习1 18个小朋友排成一队去看电影，从前往后数，胖胖排在第8个．如果从队伍的最后往前数，胖胖排在第几个？例2 朗诵小组的同学排成一排表演诗朗诵，从左边数起，玲玲是第8个，从右边数起，玲玲是第7个，有多少同学参加表演?解我们还是借助图来帮助分析、理解题意．从图中能够很清楚地看到，从左往右数时，把玲玲数了一次，从右往左数时，玲玲又被数了一次．把两次数出的人数相加时，玲玲被多加了一次．因此，把两次数出的人数相加后减去1就是实际的总人数，即8+7-1=14(个)．答：共有14个同学参加表演．随堂练习2 排排队，来报数，正着报数我报6，倒着报数我报9．请你算一算，一共有多少小朋友在报数?例3小明有10支铅笔，小红有4支铅笔，要使两人的铅笔同样多，小明要给小红几支铅笔?解我们用图表示：从图中我们可以清楚地看到，小明比小红多6支铅笔，把多出来的6支铅笔平均分成2份，即6÷2=3．答：小明给小红3支铅笔后，两人的铅笔同样多．随堂练习3 王老师有10本练习本，李老师有18本练习本，要使两人的练习本同样多，李老师要给王老师多少本练习本?例4一排有20个座位，其中有些座位已经有人，小明无论坐在哪一个座位上，旁边都有一个人与他相邻，那么原来至少有多少人已经就座?解通过分析，我们可以知道要使小明无论坐在哪一个座位上，旁边都有一个人与他相邻，也就是说两个人之间只允许有两个空位，且要考虑到如第一个座位为空位的话，第二个座位必须有人．依据以上条件，用★表示已经有人就座，用☆表示空位画图☆★☆☆★☆☆★☆☆★☆☆★☆☆★☆☆★通过画图，很快就可以找到答案了．答：原来至少有7个人已经就座．随堂练习4一排10个座位，其中有些座位已经有人，小明无论坐在哪一个座位上，旁边都有一个人与他相邻，那么原来至少有多少人已经就座?例5如图12—5，一条小街上顺次安装有10盏路灯，为了节约用电又不影响路面照明，要关闭除首末两灯以外的8盏灯中的4盎灯，但被关的灯不能相邻．一共有几种不同的关法?○○○○○○○○○○解我们把所有的情况通过画图12—6，全部列举出来：○●○●○●○●○○○●○●○●○○●○○●○●○○●○●○○●○○●○●○●○○○●○●○●○●○答：共有5种不同的关法．随堂练习5把4个一样的球放到两个相同的盒孑里，有多少种不同的方法?练习题1、二(1)班22个小朋友排成一队去操场做操，从最前面数到丁丁是第9个，君君排在丁丁的后面．从队伍的最后往前数，君君排在第几个?2、第一小队的同学排成一排，排在东东前面的有6个同学，排在东东后面的有4个同学，第一小队一共有几个同学？3、小朋友们排成一队参观博物馆，从排头数起牛牛是第10个，从排尾数起妞妞是第18个，排在牛牛前面的就是妞妞，一共有多少小朋友参观博物馆？4、在20米的校园小道一边种杨柳树，每隔4米种一颗，两端都种，想一想，一共要中几颗树？5、小明给小红4支铅笔后，两人的支数相同，问：小明比小红多几支铅笔？6、姐姐有4支铅笔，妹妹给姐姐3支铅笔后，两人的支数相同，妹妹原来有几支铅笔？7、一根16米长的木条，把它锯成4段，要锯几次？8、小丁从一楼走到四楼用了9分钟，照这样的速度，从一楼走到七楼要用多少分钟？9、妈妈到水果店买苹果，她带的钱若买3斤多1元，若买4斤少1元5角，问：妈妈带了多少钱去买苹果？10、体育小组有20个学生，排成两排队伍做早操，每两个学生之间相隔1米，每排队伍又多长？。

第十二讲图形竖式谜前续知识点：二年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲把里面的人物换成相应红字标明的人物．萱萱卡莉娅萱萱 卡莉娅卡莉娅卡莉娅，看我摆的小人，多漂亮啊！你摆的是什么啊？萱萱我不仅能摆出小人，还能摆出一头牛呢！厉害吧！哈哈~萱萱，竖式谜是一种有趣的数学问题．它的特点是给出运算式子，但式子中某些数字是用图形或者汉字来代表的，要求我们进行恰当的分析、判断和推理，从而确定这些图形或汉字所代表的数字．对于式子中的每一个位置，都可以从0至9这10个数字中选择一个，除非进行分析判断，否则想简单地直接通过试数的方法确定答案是极为费时费力的．因此，对于竖式谜必须以观察分析为基础，在此基础上才可以试数．这是竖式谜这类问题在思维顺序上的基本要求．【提示】从哪个数位入手呢？△＝（ ）☆＝（ ）△＝（ ）☆＝（ ） （1）（2）2 △ ＋△☆8 9☆ △ ＋△59 2下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？例题1（1） △＝（ ）☆＝（ ）（2）△＝（ ）☆＝（ ）△ 3 ＋ ☆ △88△ ☆ ＋ 3 △81下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？练习1【提示】相同的图形代表相同的数字哦！☆＝（ ）△＝（ ）☆＝（ ）（1）（2）☆ ☆ ＋ ☆6☆ △ ＋ △ △ 178下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？例题2☆＝（ ）△＝（ ） ☆＝（ ）（1）（2） ☆ ☆ ＋ ☆96☆ △ ＋ △ △ 1下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？练习2【提示】两个相同的数字相加得到的和是奇数还是偶数呢？△＝（ ） ☆＝（ ）△＝（ ） ☆＝（ ）（1）（2）☆ △ ＋ ☆ △86☆ △ ＋☆△7 4 下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？ 例题3△＝（ ） ☆＝（ ）△＝（ ） ☆＝（ ）（1）（2）☆ △ ＋ ☆ △ 128☆ △ ＋ ☆ △92下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？练习3【提示】个位和十位上的两个数字相同．练习4 下面加法竖式中的“★”、“◎”各代表什么数字？请你写出两种答案．★＝（ ） ◎＝（ ）★＝（ ） ◎＝（ ）★ ◎ ＋ ◎ ★88下面加法竖式中的“★”、“◎”各代表什么数字？请你写出两种答案．例题4★＝（ ） ◎＝（ ）★＝（ ） ◎＝（ ）★ ◎ ＋◎ ★66【提示】一个两位数加一个两位数，最多能得到一个多大的三位数呢？【提示】两个数字相加有进位时，最多进几？“★”、“△”和“◎”分别代表三个不同的数字．请找出它们分别代表的数字，把这个竖式补充完整．1 ＋ ★ ★ ◎ △ △★＝（ ） ◎＝（ ） △＝（ ）例题6“★”、“△”和“◎”分别代表三个不同的数字．请找出它们分别代表的数字，把这个竖式补充完整．例题5★＝（ ） ◎＝（ ） △＝（ ）★ ◎ ＋ ◎ ◎ ★★△课堂内外小知识——数字诗数字诗，一般指诗中句句或多句含数字．诗歌创作的技巧很多,数字入诗乃技巧之一．巧用数字入诗，在古代诗歌中屡见不鲜，给人以新奇、独特之感，颇具回味．宋朝邵雍（康节）有一首五言数字诗《山村咏怀》，清新简单，朴实自然，堪称经典．诗云：一去二三里，烟村四五家；门前六七树，八九十枝花．明朝吴承恩有七言诗《明月夜静图》，是包含一到十的数字诗，比较受推崇．诗云：十里长亭无客走，九重天上现星辰．八河船只皆收港，七千州县尽关门．六宫五府回官宅，四海三江罢钓纶．两山楼头钟鼓响，一轮明月满乾坤．作业1. 下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？2. 下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？3. 下面的加法竖式中，相同的图形代表相同的数字，不同的图形代表不同的数字．那么“△”、“☆”各代表什么数字？4. 下面加法竖式中的“★”、“◎”各代表什么数字？请你写出两种答案．△＝（ ） ☆＝（ ）（1）△＝（ ） ☆＝（ ）（2）☆ △ ＋ ☆ △38☆ △ ＋ ☆ △ 164☆ △＋ △ △ 166△＝（ ） ☆＝（ ）（2）☆＝（ ）☆ ☆＋ ☆84（1）6 △ ＋ △ ☆97（1）△＝（ ） ☆＝（ ）（2） △＝（ ） ☆＝（ ）△ ☆＋ 2 △515. “★”、“△”和“◎”分别代表三个不同的数字．找出它们分别代表的数字，把竖式补充完整．★＝（ ） ◎＝（ ） △＝（ ）◎★ ＋ ◎ △ ★ △ ◎★ ◎ ＋ ◎ ★ 7 7★＝（ ） ◎＝（ ）★＝（ ） ◎＝（ ）第十二讲 图形竖式谜1. 例题1答案：（1）△＝5，☆＝3；（2）△＝4，☆＝7详解：加法竖式谜，从已知数字较多的数位入手．（1）从个位来看：△835=-=，则十位无进位，所以☆853=-=．所以△＝5，☆＝3．（2）从十位看：因为加法竖式中可能有进位，但是两个数字相加，最多进“1”，所以△835=-=或△8314=--=．当△＝5时，说明个位没有向十位进位“1”，从个位判断☆51+=，☆没有合适数字，所以△＝5不符合题意；那么当△＝4时，说明个位向十位进位“1”，从个位判断☆41+=，所以☆1147=-=．所以△＝4，☆＝7．2. 例题2答案：（1）☆＝8；（2）△＝5，☆＝4详解：在给出的图形较多的竖式中，从相同图形较多的数位入手．（1）从个位入手，☆+☆＝6，则☆为3或8．如果☆为3，十位就不符合，那么☆为8，向十位进1，819+=．所以☆＝8．（2）从个位入手，△+△＝0，则△为0或5．如果△为0，则十位不符合，那么△为5，向十位进1，可以得出☆10154=--=．所以△＝5，☆＝4．3. 例题3答案：（1）△＝4，☆＝6；（2）△＝6，☆＝4详解：当竖式数位上出现的相同图形个数一样多时，尽量按照竖式的计算顺序解题，即从个位入手．（1）两个相同的数字相加，得数是8，那么可以考虑这个数字是4或9．如果个位是4，那么没有进位，十位得数是2，可以考虑是1和6，而百位有进位，所以排除了十位是1的情况，那么十位是6；个位还可能是9，如果是9的话，就有进位，那么十位原来的两个数相加的和就是1或11，而十位的两个数是相同的，不可能出现奇数的情况，所以个位只能是4．所以△＝4，☆＝6．（2）看个位，两个相同的数相加，得数是2，那么可以考虑这个数是1和6，如果个位是1，那么没有进位，十位得数是9，两个相同的数相加的和是偶数，不存在两个相同的数相加为9，所以个位是6，向十位进1，所以十位上的两个相同的数相加就为8，那么这个数是4．所以△＝6，☆＝4．4. 例题4答案：★＝1，◎＝5；★＝2，◎＝4详解：个位和十位都是一样的数，和相同，可以确定加法竖式中没有进位．那么可以从比6小的数字举例子，当◎＝1时，那么★＝5；当◎＝2时，那么★＝4……，依次列举．注意当◎＝3时，那么★＝3，这个结果是不符合题意的，因为，“★”和“◎”代表的数字不相同．答案不唯一．5. 例题5答案：★＝1，◎＝9，△＝8详解：从首位分析，因为两个数字相加最多进1，百位有一个进位，那么可知★＝1，代入原竖式，如下图．由于十位有进位，所以可知：◎＝9，这时候得到△＝8．注意，竖式中有进位一定要把进位标上，以防忘记．6. 例题6答案：★＝9，◎＝1，△＝0详解：从首位分析，因为两个数字相加最多进1，百位有一个进位，那么可知◎＝1，代入原竖式，如下图．由于十位有进位，所以可知：★＝9，这时候从个位得到△＝0．注意，竖式中有进位一定要把进位标上，以防忘记．7. 练习1答案：（1）△＝6，☆＝3；（2）△＝7，☆＝1简答：加法竖式谜，从已知数字较多的数位入手．（1）从十位看：因为加法竖式中可能有进位，但是两个数字相加，最多进“1”，所以△826=-=或△8215=--=．当△＝6时，说明个位没有向十位进位“1”，从个位判断6+☆＝9，☆963=-=；那么当△＝5时，说明个位向十位进位“1”，从个位判断5+☆＝9，☆19514=-=，因为☆表示的是一个数字，所以△＝5不符合题意．所以△＝6，☆＝3．（2）从个位看：△52+=，则个位一定向十位进位“1”，所以△1257=-=；从十位判断：☆719++=，☆9711=--=．所以△＝7，☆＝1．8. 练习2答案：（1）☆＝5；（2）△＝9，☆＝7简答：在给出的图形较多的竖式中，从相同图形较多的数位入手．（1）从个位入手，☆+☆＝0，则☆为0或5．如果☆为0，十位就不符合，那么☆为5，向十位进1，516+=．所以☆＝5．（2）从个位入手，△+△＝8，则△为4或9．如果△为4，则十位不符合，那么△为9，向十位进1，可以得出☆17197=--=．所以△＝9，☆＝7．1 ＋★ ★1 △△ 11 ◎ ＋◎ ◎1 1△ 1 19.练习3答案：（1）△＝3，☆＝4；（2）△＝8，☆＝2简答：两个相同的数字相加，得数是6，那么可以考虑这个数字是3或8．如果个位是3，那么没有进位，十位得数是8，那么☆＝4；个位还可能是8，如果是9的话，就有进位，那么十位原来的两个数相加的和就是7，而十位的两个数是相同的，不可能出现奇数的情况，所以个位只能是4．所以△＝3，☆＝4．（2）看个位，两个相同的数相加，得数是4，那么可以考虑这个数是2或7，如果个位是2，那么没有进位，十位得数是7，两个相同的数相加的和是偶数，不存在两个相同的数相加为7，所以个位是7，向十位进1，所以十位上的两个相同的数相加就为6，那么这个数是3．所以△＝7，☆＝3．10.练习4答案：◎＝1，★＝7；◎＝2，★＝6简答：个位和十位都是一样的数，和相同，可以确定加法竖式中没有进位，且“★”和“◎”代表的数字不相同．那么可以从比8小的数字举例子，当◎＝1时，那么★＝7；当◎＝2时，那么★＝6……，依次列举．注意：当◎＝4时，那么★＝4，这个结果不符合题意．答案不唯一．11.作业1答案：（1）△＝3，☆＝4；（2）△＝2，☆＝9简答：从已知数多数位的入手．12.作业2答案：（1）☆＝7；（2）△＝8，☆＝7简答：观察竖式谜的特点，（1）中三个数都是一样的，那么由个位分析，只能是 2 或者7，通过排除法就可以得到正确答案；同理可以判断（2）．13.作业3答案：（1）△＝2，☆＝8；（2）△＝9，☆＝1简答：两个相同的数相加和为偶数，由此可知，（1）中没有进位，（2）中有进位．14.作业4答案：（1）★＝1，◎＝6；（2）★＝2，◎＝5简答：个位和十位都是一样的数，和相同，可以确定加法竖式中没有进位，且“★”和“◎”代表的数字不相同．那么可以从比7小的数字举例子，当◎＝1时，那么★＝6；当◎＝2时，那么★＝5……，依次列举．答案不唯一．15.作业5答案：★＝1，◎＝9，△＝8简答：首先确定★是1，然后从个位开始推断，个位△不可能是9，就说明没有进位，那么△只能是偶数，而且◎要比5大，通过尝试得出答案．。

第十一讲移多补少【专题简析】在我们的日常生活中，有很多不相等的情况，如姐姐有10支铅笔，弟弟有8支铅笔，两人的支数不相等。

有时为需要，要把不相等转换成相等，应该怎么办呢？要把不相等转换成相等，就要移多补少，也就是把多出来的部分平均分成两份，其中一份补给少的，这样就一样多了。

要特别注意的是，不能把多出来的部分全部给少的，否则又不相等了。

【例题1】开心超人有14张纪念邮票，甜心超人有10张纪念邮票，要使两人的邮票张数同样多，开心超人应给甜心超人几张邮票？思路导航：根据题意，用下图表示题中的条件。

从图中可以看出，开心超人邮票的张数比甜心超人多14-10=4（张），将多出的4张邮票平均分成2份，4÷2＝2 （张），把开心超人的2张邮票给甜心超人，那么，他们两个人的邮票张数就同样多了。

解：14－10＝4（张）4÷2＝2（张）答：要使两人的邮票张数同样多，开心超人应给甜心超人2张邮票。

练习11.二（1）班有24个足球，二（2）班有16个足球，要使两个班的足球数量相同，二（1）班应给二（2）班几个足球？2.小红有10枝铅笔，小军有6枝铅笔，小红给小军几枝铅笔后，两人的铅笔数就一样多了？3.姐姐和妹妹做红五角星，姐姐做了22个，妹妹做了10个，姐姐给妹妹几个，两人的红五角可以一样多？【例题2】姐姐和妹妹各有一些糖块，姐姐比妹妹多8块，要使两人的糖块一样，姐姐应给妹妹几块糖？思路导航：根据题中条件“姐姐比妹妹多8块”，把“多的8块”平均分成2份，8÷2＝4（块），即把姐姐的4块给娃娃，两人就同样多了。

解：8÷2＝4（块）答：要使两人的糖块一样我，姐姐应给妹妹4块糖。

练习21.小红和小明各有一些铅笔，小红比小明多6枝，要使两人的铅笔一样多，小红应该给小明几枝？2.男同学和女同学排队，男同学比女同学少10名，要使两队人数同样多，应该调几名女同学到男同学的队里？3.小刚和小军各有一些纸风车，小刚比小军多6架，要使两人的纸风车一样多，小刚应给小军几架？【例题3】欢欢把自己的3枝铅笔给飞飞后，两人的铅笔枝数就同样多了。

第十二讲加减法竖式谜前续知识点：二年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲听说沙漠地区有一个鬼国，咱们要不要去看看？好啊好啊！好啊好啊！大家看，这就是进入鬼国的大门！真的吗？终于找到了，赶紧想办法进去吧！嘿嘿，想进去不是不可以，但必须和我对个暗号，对正确了才能进去，这是鬼国的规矩！天啊，门竟然会说话，太恐怖了，快跑呀！你们两个胆小鬼别跑！我能对出暗号啊！阿呆阿呆阿呆阿呆阿瓜阿瓜阿瓜阿瓜小高小高小高小高□□＋ 21 0 0把里面的人物换成相应红字标明的人物．竖式谜，就是把一个计算时列出的完整竖式，去掉几个数字后，让同学们来补全这个竖式的一类问题．在列竖式计算时，都是从个位开始依次向高位进行计算，并且在计算时要考虑进位．同样，同学们在处理竖式谜问题时也要注意这两点．解决竖式谜问题时，经常使用末位分析法，即从个位往前分析．在加法竖式谜中，先把能确定的位置填出来，再根据进位来判断剩下的空格．在处理进位时，要注意：两个数字相加，每一位最多进“1”；三个数字相加，每一位最多进“2”．例题1在下图空格里填入适当的数字，使竖式成立。

【提示】利用末位分析法解决简单的加法竖式谜，从个位分析，注意进位，有进位先标进位．练习1在下图空格里填入适当的数字，使竖式成立．当末位分析法不能解决问题时，可以考虑首位分析法，即从最高位分析．较特殊的是“黄金三角”类型的题，注意标进位．如下图所示，在下面的6个“□”中能确定的是百位为“1”，十位从上到下分别为“9”、“0”，这三个位置正好拼成了一个“三角形”，这就是我们说的“黄金三角”．6 □ □＋ □ 6 69 433 9 ＋□6□□ □ □3□ 6 □ ＋ 6 □ 69623＋□ □□ □2在碰到类似的竖式谜时，先找到“黄金三角”，然后在这三个“□”中依次填入“1”、“9”、“0”．例题2在下图空格里填入适当的数字，使竖式成立。

【提示】当从个位分析（即末位分析）行不通时，要从首位（即最高位）进行分析，因为两个数字相加最多进“1”，所以首位一定是“1”．练习2在下图空格里填入适当的数字，使竖式成立．除了最基本的竖式谜之外，有些竖式谜对于所填的空格还有特殊的要求，这就需要我们在解决这些问题时，不仅考虑到之前提到的那些要素，还要注意题目中的特殊要求．例题3如下图，用0、1、2、3、4、5、6、7、8、9这10个数字各一次，组成一个正确的加法竖式。

第十二讲加减法竖式谜前续知识点：二年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲听说沙漠地区有一个鬼国，咱们要不要去看看？好啊好啊！好啊好啊！大家看，这就是进入鬼国的大门！真的吗？终于找到了，赶紧想办法进去吧！嘿嘿，想进去不是不可以，但必须和我对个暗号，对正确了才能进去，这是鬼国的规矩！天啊，门竟然会说话，太恐怖了，快跑呀！你们两个胆小鬼别跑！我能对出暗号啊！阿呆阿呆阿呆阿呆阿瓜阿瓜阿瓜阿瓜小高小高小高小高□□＋ 21 0 0把里面的人物换成相应红字标明的人物．竖式谜，就是把一个计算时列出的完整竖式，去掉几个数字后，让同学们来补全这个竖式的一类问题．在列竖式计算时，都是从个位开始依次向高位进行计算，并且在计算时要考虑进位．同样，同学们在处理竖式谜问题时也要注意这两点．解决竖式谜问题时，经常使用末位分析法，即从个位往前分析．在加法竖式谜中，先把能确定的位置填出来，再根据进位来判断剩下的空格．在处理进位时，要注意：两个数字相加，每一位最多进“1”；三个数字相加，每一位最多进“2”．例题1在下图空格里填入适当的数字，使竖式成立。

【提示】利用末位分析法解决简单的加法竖式谜，从个位分析，注意进位，有进位先标进位．练习1在下图空格里填入适当的数字，使竖式成立．当末位分析法不能解决问题时，可以考虑首位分析法，即从最高位分析．较特殊的是“黄金三角”类型的题，注意标进位．如下图所示，在下面的6个“□”中能确定的是百位为“1”，十位从上到下分别为“9”、“0”，这三个位置正好拼成了一个“三角形”，这就是我们说的“黄金三角”．6 □ □＋ □ 6 69 433 9 ＋□6□□ □ □3□ 6 □ ＋ 6 □ 69623＋□ □□ □2在碰到类似的竖式谜时，先找到“黄金三角”，然后在这三个“□”中依次填入“1”、“9”、“0”．例题2在下图空格里填入适当的数字，使竖式成立。

【提示】当从个位分析（即末位分析）行不通时，要从首位（即最高位）进行分析，因为两个数字相加最多进“1”，所以首位一定是“1”．练习2在下图空格里填入适当的数字，使竖式成立．除了最基本的竖式谜之外，有些竖式谜对于所填的空格还有特殊的要求，这就需要我们在解决这些问题时，不仅考虑到之前提到的那些要素，还要注意题目中的特殊要求．例题3如下图，用0、1、2、3、4、5、6、7、8、9这10个数字各一次，组成一个正确的加法竖式。