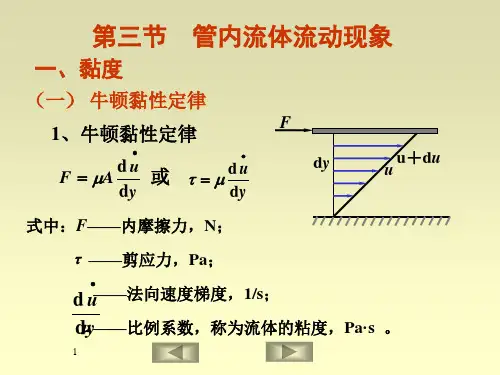
管内流体流动现象

第一章 流体流动§4 流体在管内流动时的摩擦阻力损失本节重点：直管阻力与局部阻力的计算，摩擦系数的影响因素。

难点：用量纲分析法解决工程实际问题。

流动阻力的大小与流体本身的物理性质、流动状况及壁面的形状等因素有关。

化工管路系统主要由两部分组成，一部分是直管，另一部分是管件、阀门等。

相应流体流动阻力也分为两种：直管阻力：流体流经一定直径的直管时由于内摩擦而产生的阻力； 局部阻力：流体流经管件、阀门等局部地方由于流速大小及方向的改变而引起的阻力。

一 范宁公式（Fanning ）1、范宁公式 ：范宁经过理论推导，得到了以下公式： 22l u h f d λ= （1-53） 式（1-53）为计算流体在直管内流动阻力的通式，称为范宁（Fanning ）公式。

式中λ为无量纲系数，称为摩擦系数或摩擦因数，与流体流动的Re 及管壁状况有关。

式（1－53）也可以写成：22u d l h p f f ρλρ==∆ （1－54） 应当指出，范宁公式对层流与湍流均适用，只是两种情况下摩擦系数λ不同。

2、管壁粗糙度对摩擦系数λ的影响光滑管：玻璃管、铜管、铅管及塑料管等称为光滑管；粗糙管：钢管、铸铁管等。

管道壁面凸出部分的平均高度，称为绝对粗糙度，以ε表示。

绝对粗糙度与管径的比值即dε，称为相对粗糙度。

工业管道的绝对粗糙度数值见教材（P27表1－1）。

管壁粗糙度对流动阻力或摩擦系数的影响，主要是由于流体在管道中流动时，流体质点与管壁凸出部分相碰撞而增加了流体的能量损失，其影响程度与管径的大小有关，因此在摩擦系数图中用相对粗糙度dε，而不是绝对粗糙度ε。

流体作层流流动时，流体层平行于管轴流动，层流层掩盖了管壁的粗糙面，同时流体的流动速度也比较缓慢，对管壁凸出部分没有什么碰撞作用，所以层流时的流动阻力或摩擦系数与管壁粗糙度无关，只与Re有关。

流体作湍流流动时，靠近壁面处总是存在着层流内层。

如果层流内层的厚度δL大于管壁的绝对粗糙度ε，即δL>ε时，如图1-28（a）所示，此时管壁粗糙度对流动阻力的影响与层流时相近，此为水力光滑管。

管道流体原理管道是一种常见的输送流体的工程结构，广泛应用于石油、化工、水利、供热等领域。

了解管道流体原理对于设计和操作管道系统至关重要。

本文将介绍管道流体的基本原理以及与之相关的一些重要概念和公式。

一、流体基本概念流体是指在外力作用下可以流动的物质，包括液体和气体。

与固体相比，流体的分子间距较大，分子间相互作用力较小，因此具有流动性。

流体的性质可通过以下两个基本参数来描述：1. 密度（ρ）：流体单位体积的质量，通常以千克/立方米（kg/m³）表示。

2. 粘度（μ）：流体内部抵抗剪切力的能力，即流体的黏稠程度，通常以帕斯卡秒（Pa·s）表示。

二、流体力学中的基本定律1. 连续方程：根据质量守恒定律，流体在管道中的质量守恒可由连续方程描述。

连续方程的数学表达为：∂ρ/∂t + ∇·(ρv) = 0其中，∂ρ/∂t表示流体密度随时间的变化率，∇·(ρv)表示流体质量流入单位面积内的变化率。

2. 动量方程：根据动量守恒定律，流体在管道中的动量守恒可由动量方程描述。

动量方程的数学表达为：∂(ρv)/∂t + ∇·(ρv⃗v) = -∇P + ∇·τ + ρg⃗其中，∂(ρv)/∂t表示流体动量随时间的变化率，∇·(ρv⃗v)表示流体动量流入单位面积内的变化率，∇P表示压力梯度，∇·τ表示剪应力的散度，ρg⃗表示重力作用力。

三、流体在管道中的流动状态管道中的流体可分为层流和湍流两种流动状态。

1. 层流：当流体在管道中呈现出较为有序的分层流动状况时，称为层流。

层流时，流体的速度随距离变化较平缓，流线间相对稳定，分子间相互作用力起主导作用。

层流的特点是低速、流线整齐。

2. 湍流：当流体在管道中呈现出非线性、脉动和流线交错等现象时，称为湍流。

湍流时，流体的速度和压力有大幅度波动，分子间相互作用力起次要作用。

湍流的特点是高速、流线混乱。

刘体流动过程管内流体流动现象刘体流动过程是管道内流体流动的一种现象。

流体流动的基本原理是流体在管道内受力的作用下产生的运动。

在实际应用中，流体流动现象广泛存在于各个领域，如工业生产、交通运输、能源供应等。

本文将从流体运动的基本特征、数学描述、流动类型和流体运动的影响因素等方面进行论述，以便更好地理解刘体流动过程。

一、刘体流动的基本特征1.流体的连续性：刘体流动过程中，粒子之间的距离虽然会发生变化，但流体质点间距离的变化不大，整个流体质点仍然保持着连续的状态。

2.流体的非黏性：刘体流动过程中，流体质点之间的摩擦力相对较小，不会对流体的流动性质产生重要影响。

3.流体的不可压性：刘体流动过程中，流体质点相对变动量较小，流体密度基本不变。

4.流体的运动速度不同：刘体流动过程中，流体质点之间的运动速度不同，导致流速梯度的产生。

流体速度最大的地方为流体的中心轴线，流体速度逐渐减小，最靠近管道壁的地方速度最小。

二、刘体流动的数学描述刘体流动过程可以通过对连续介质流动的描述来进行数学建模。

在不同的情况下，刘体流动可以通过不同的数学模型来描述。

常用的数学模型有连续介质方程、动量方程、能量方程和物质守恒方程。

这些方程可以用来描述流体的流动特性，如速度分布、压力分布等。

在实际应用中，可以通过求解这些方程来预测流体流动的行为。

三、刘体流动的类型刘体流动可以分为层流和湍流两种类型。

1.层流：层流是指流体质点在流动过程中遵循谢姆的流体力学规律，流体质点的运动方式有序，并且流速的分布是有规律的。

层流一般发生在低速流或小管径情况下，流体的运动速度不超过一定的临界速度。

2.湍流：湍流是指流体质点在流动过程中运动不规则，流速分布无序的流动方式。

湍流一般发生在高速流或大管径情况下，流体的运动速度超过临界速度。

四、刘体流动的影响因素刘体流动的行为受到多种因素的影响，包括以下几个方面：1.管道形状：管道形状对刘体流动的行为有着重要的影响。

管道中的液体流动管道中的液体流动是液体在管道中运动和传输的过程。

液体流动在日常生活和工业生产中起着重要的作用，涉及到很多领域，如供水、石油输送、化学工程等。

了解液体在管道中的流动规律，对于管道设计、操作和维护都具有重要意义。

一、液体流动的原理液体流动的原理主要涉及两个重要的物理学定律，即贯穿流方程和伯努利定律。

1. 贯穿流方程贯穿流方程是描述液体流动的基本方程之一，可以表示为：Q = Av其中，Q是液体的流量，A是流体通过管道横截面的面积，v是液体的流速。

贯穿流方程表明，在单位时间内通过管道单位面积的液体流动的体积等于液体的流速乘以管道的横截面积。

2. 伯努利定律伯努利定律是描述液体在流动过程中能量转换的定律，可以表示为：P + 1/2ρv² + ρgh = 常数其中，P是液体的压力，ρ是液体的密度，v是液体的流速，g是重力加速度，h是液体的高度。

伯努利定律表明，在液体流动中，液体的压力、速度和重力势能之间存在着相互转换的关系。

二、管道中的液体流动类型在管道中，液体的流动可以分为层流和湍流两种类型。

1. 层流层流是指液体在管道中呈现出规则的、无交错的流动状态。

在层流中，液体的流速是均匀的，流体粒子的速度分布呈现顺序排列，层与层之间不存在明显的混合和对流的现象。

层流具有流速低、流动平稳和粘性损失小等特点。

2. 湍流湍流是指液体在管道中呈现出不规则的、随机的流动状态。

在湍流中，液体的流速不均匀，流体粒子的速度呈现混乱的分布，存在着涡流和涡旋的运动。

湍流具有流速高、流动不稳定和粘性损失大等特点。

三、影响管道液体流动的因素管道液体流动受到多种因素的影响，主要包括以下几个方面：1. 管道的几何形状管道的几何形状直接影响液体的流速和流量。

例如，管道的直径和长度会影响液体流动的阻力和压力损失，管道的弯曲和收缩等处会引起液体的湍流和涡流现象。

2. 液体的性质液体的粘度、密度和流变性质等都会对液体的流动特性产生影响。