当前位置：文档之家 › 流体的流动现象

流体的流动现象

  • 格式：doc
  • 大小：309.50 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

管内流体流动现象

管内流体流动现象


（1-27）
其单位为m2/s。显然运动粘度也是流体的物理
性质。
二、流体的流动型态
1、两种流型——层流和湍流 图1-18为雷诺实验装置示意图。水箱装有溢流装置， 以维持水位恒定，箱中有一水平玻璃直管，其出口 处有一阀门用以调节流量。水箱上方装有带颜色的 小瓶，有色液体经细管注入玻璃管内。
图1-17 流体在管内的速度分布
实验证明，对于一定的流体，内摩擦力F与两流体 层的速度差成正比，与两层之间的垂直距离dy成 反比，与两层间的接触面积A成正比，即
.

F A（ddyu1-26）
式中：.F——内摩擦力，N；
du

—dy —法向速度梯度，即在与流体流动方向相垂直的
y方向流体速度的变化率，1/s；
2． 湍流时的速度分布 湍流时的速度分布目前尚不能利用理论推导获得，而是通过
实验测定，结果如图1-22所示，其分布方程通常表示成以下 形式：
图1-22 湍流时的速度分布
四、流体流动边界层
图1-19 流体流动型态示意图
2、流型判据——雷诺准数
流体的流动类型可用雷诺数Re判断。
Re d（u1-28）


Re准数是一个无因次的数群。
大量的实验结果表明，流体在直管内流动时， （1）当Re≤2000时，流动为层流，此区称为层流区； （2）当Re≥4000时，一般出现湍流，此区称为湍流区； （3）当2000< Re <4000 时，流动可能是层流，也可
μ——比例系数，称为流体的粘度或动力粘度，Pa·s。
一般，单位面积上的内摩擦力称为剪应力，以τ表
示，单位为Pa，则式（1-26）变为
.

第一章 流体流动2..

第一章 流体流动2..

）
盐城师范学院
---化工原理---
1.４.2 流体在圆管内的速度分布 速度分布：流体在圆管内流动时,管截面上 质点的速度随半径的变化关系。 无论是滞流或湍流，在管道任意截面上，流体质点的速度 沿管径而变化，管壁处速度为零，离开管壁以后速度渐增， 到管中心处速度最大。速度在管道截面上的分布规律因流 型而异。
层流边界层 湍流边界层
u∞
u∞
u∞
δ
A x0
层流内层
平板上的流动边界层
盐城师范学院
转折点：
Re x
u x
---化工原理---

5 105 ~ 2 106
边界层厚度δ随x增加而增加
层流： 4.64 x (Rex )0.5
层流边界层
湍流边界层
x
x
0.5
u∞
u∞
u∞
湍流： 0.376 0.2
(a)
过渡流
(b)
湍流 (Turbulent flow)
(c)
两种稳定的流动状态：层流、湍流。
盐城师范学院
---化工原理---
层流：
* 流体质点做直线运动；
* 流体分层流动，层间不相混合、不碰撞； * 流动阻力来源于层间粘性摩擦力。 湍流： 主体做轴向运动，同时有径向脉动；
特征：流体质点的脉动 。
r2 u umax 1 R 2
盐城师范学院
---化工原理---
r2 dVs umax 2r 1 R 2 dr
积分此式可得
2 r r R Vs 2umax r 0 r 1 R 2 dr R 2 4 r r 2umax 2 R 2u / 2 max 2 4R 0

1.4 流体流动现象

1.4 流体流动现象
第1章 （第4节） 流体流动现象
4 边界层的概念





讨论 ⑴边界层分离的必要条件： 流体具有粘性； 流动过程中存在逆压梯度。 ⑵边界层分离的后果： 产生大量旋涡； 造成较大的能量损失。 ⑶流体沿着壁面流过时的阻力称为摩擦阻力。 由于固体表面形状而造成边界层分离所引起的能 量损耗称为形体阻力。 ⑷粘性流体绕过固体表面的阻力为摩擦阻力与形 体阻力之和这两者之和又称为局部阻力。
M L L3 L0 M 0 0 M L


Re ⑶Re准数是一个无因次的数群。
L
第1章 （第4节） 流体流动现象
1 流动类型与雷诺准数

⑷流体的流动类型可用雷诺数Re判断。
Re 2000时为层流

流体质点仅沿着与管轴平行的方向作直线运动，质点无 径向脉动，质点之间互不混合,不碰撞。
1 流动类型与雷诺准数

⑵ 调节阀门开度， 使流量变大，细管 内有色液体成波浪 形。说明流体质点 除沿轴向流动外， 沿径向也运动。相 邻流体层之间混合， 碰撞。 （如动画）
第1章 （第4节） 流体流动现象
1 流动类型与雷诺准数

⑶调节阀门开度，使
流量再变大，细管内 有色液体细线便完全 消失，有色液体出细 管后完全散开，与水 混合在一起。说明流 体质点除沿轴向流动 外，还作不规则杂乱 运动。彼此之间混合， 碰撞。 （如动画）
齐齐哈尔大学
第1章 （第4节） 流体流动现象
1.4 流体流动现象
1 流动类型与雷诺准数
本节 讲授 内容
2 流体在圆形直管内速度分布 3 滞流与湍流的比较
4 边界层的概念
第1章 （第4节） 流体流动现象

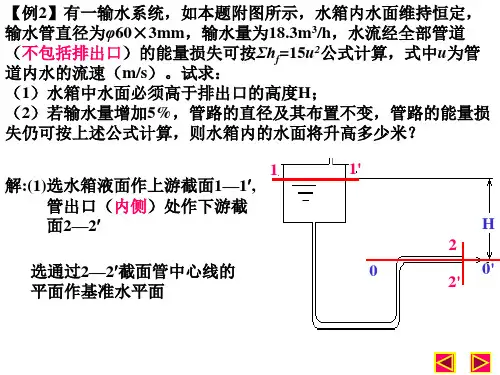
化工原理第一章第四节流体流动现象

化工原理第一章第四节流体流动现象

任意截面的总机械能是相等的，即:
3000
6 6'
E1 E2 E3 E4 E5 E6 E
2 2'
2 2 u12 p1 u2 p2 u3 p3 E gz1 gz2 gz3 2 2 2 2 2 2 u4 p4 u5 p5 u6 p6 gz4 gz5 gz6 2 2 2
式中:
2 1
2
1 h 2
1
u2 2 m
s
2 2
2
d2 184 而u1 u2 2 6.7712m s 100 d1
hf1-2=11.38J/kg
Hale Waihona Puke u u p1 z1g p2 z2 g h f 12 2 2
2 2
2 2' 24m
2m 1 1'
u1 p1 u2 p2 gz1 we gz2 h f 12 2 2
由已知： Z1=0,
Z2=24+2=26m,
P1=0(表） u10
P2= 6.15×104Pa(表压)
hf1-2= 160J/kg
Vs 34.5 u2 2.49 m s 2 2 d 0.07 3600 4 4
1000 500
【例4】水在本题附图所示的虹吸管内作定态流动，管路直 径没有变化，水流经管路的能量损失可以忽略不计，试计 算管内截面2-2 、3-3、4-4 、5-5 处的压强。大气压强为 1.0133×105Pa。图中所标注的尺寸均以mm计。 4 解： 选择2-2 截面做基准水平面 4' 3 3' 理想流体，没有外部能量加入， 1 1' 5 5' 因此，根据理想流体柏努利方程，

化工原理第一章(流体的流动现象)

化工原理第一章(流体的流动现象)

ρ(
∂v ∂v ∂v ∂v ∂p ∂ ∂v 2 r ∂ ∂v ∂w ∂ ∂u ∂v + u + v + w ) = k y − + µ(2 − ∇v) + µ( + ) + µ( + ) ∂t ∂x ∂y ∂z ∂y ∂y ∂y 3 ∂z ∂z ∂y ∂x ∂y ∂x
2012-4-18
湍 流 的 实 验 现 象
2012-4-18
（3）流体内部质点的运动方式（层流与湍流的区别） ）流体内部质点的运动方式（层流与湍流的区别） ①流体在管内作层流流动 层流流动时，其质点沿管轴作有规 有规 层流流动 互不碰撞，互不混合 则的平行运动，各质点互不碰撞 互不混合 的平行运动 互不碰撞 互不混合。 ②流体在管内作湍流流动 湍流流动时，其质点作不规则的杂 湍流流动 不规则的杂 乱运动，并互相碰撞混合 互相碰撞混合，产生大大小小的旋涡 旋涡。 乱运动 互相碰撞混合 旋涡 管道截面上某被考察的质点在沿管轴向 轴向运动的同时 轴向 ，还有径向 径向运动（附加的脉动 脉动）。 径向 脉动
du F = µA dy
式中：F——内摩擦力，N； du/dy——法向速度梯度 法向速度梯度，即在与流体流动方向相垂直的 法向速度梯度 y方向流体速度的变化率，1/s； µ——比例系数，称为流体的粘度或动力粘度 粘度或动力粘度，Pa·s。 粘度或动力粘度
2012-4-18
【剪应力 剪应力】 剪应力 【定义 定义】单位面积上的内摩擦力称为剪应力 剪应力，以τ表 定义 剪应力 示，单位为Pa。
ρ(
2012-4-18
著名的“纳维-斯托克斯方程”，把流体的速度、压力、密 度和粘滞性全部联系起来，概括了流体运动的全部规律；只 是由于它比欧拉方程多了一个二阶导数项，因而是非线性的 ，除了在一些特殊条件下的情况外，很难求出方程的精确解 。分析这个方程的性态，“仿佛是在迷宫里行走，而迷宫墙 的隔板随你每走一步而更换位置”。计算机之父冯·诺意曼（ Neumann，Joha von 1903～1957）说：“这些方程的特性…… 在所有有关的方面同时变化，既改变它的次，又改变它的阶 。因此数学上的艰辛可想而知了。 有一个传说，量子力学家海森伯在临终前的病榻上向上帝提 有一个传说 了两个问题：上帝啊！你为何赐予我们相对论 相对论？为何赐予我 相对论 们湍流 湍流？海森伯说：“我相信上帝也只能回答第一个问题” 湍流 。

流体流动现象

流体流动现象
2021/3/16
A→C：流道截面积逐渐减
小，流速逐渐增加，压力
逐渐减小，d P 0（顺压梯 dx
度）；
C→S：流道截面积逐渐增
加，流速逐渐减小，压力
逐渐增加，d P 0 （逆压梯
度）
dx
B
A
S
S点：物体表面的流体质点在逆 压梯度和粘性剪应力的作用下， 速度降为0。
SS’以下：边界层脱离固体壁面，而后倒流回来，形成涡流， 出现边界层分离。
1）圆管内层流流动的速度分布
dr
p1
r
p2 R
τr
l
微元体受力分析：
作用于流体单元左端的总压力为：P1 r2p1
2021/3/16
作用于流体单元右端的总压力为： P2 r2p2
作用于流体单元四周的黏滞力为： Fr2rl
r
dur dr
F 2rl dur
dr
r2p 1r2p 22 rld d u rr0
2021/3/16
讲授内容
2021/3/16
1.1 流体静止的基本方程 1.2 流体流动的基本方程 1.3 流体流动现象 1.4 流体在管内的流动阻力 1.5 管路计算 1.6 流速和流量测量
1.3 流体流动现象
1 牛顿黏性定律与流体的黏度
本节 讲授 内容
2 流动类型与雷诺准数 3 滞流与湍流的比较
dr
R
r
l
流体通过微圆环体积流量为：
dVs 2rudr
滞流时，管截面上速度分布为：
u
umax
1
r2 R2
2021/3/16
dV sumax2r1R r22dr
积分此式可得：
Vs 2umax

化工原理 第一章 流体的流动现象

化工原理 第一章 流体的流动现象
N.s / m2
/
m3
m0kg0s0
2019/8/3
4、流动形态的判别方法 大量的实验结果表明，流体在直管内流动时：
（1）当Re≤2000时，流动为层流，此区称为层流区； （2）当Re≥4000时，一般出现湍流，此区称为湍流 区； （3）当2000< Re <4000 时，流动可能是层流，也可 能是湍流，与外界干扰有关，该区称为不稳定的过 渡区。
2019/8/3
【例】20℃的水在内径为50mm的管内流动，流速为 2m/s，试分别用SI制和CGS制计算Re数的数值。
注意：在计算Re时，一定要注意各个物理量的单位 必须统一。
【解】（1）用SI制计算：从附录五查得20℃时：
ρ=998.2kg/m3，μ=1.005mPa.s，
已知：管径d=0.05m，流速u=2m/s，
2019/8/3
【剪应力】 【定义】单位面积上的内摩擦力称为剪应力，以τ表 示，单位为Pa。
前式可改变为： du
dy
【结论】 流体层间的内摩擦力或剪应力与法向速度 梯度成正比。
2019/8/3
（6）牛顿型流体非牛顿型流体
【牛顿型流体】剪应力与速度梯度的关系符合牛顿 粘性定律的流体，包括所有气体和大多数液体； 【非牛顿型流体】不符合牛顿粘性定律的流体，如 高分子溶液、胶体溶液及悬浮液等。
2019/8/3
飞机的“隐形杀手”－晴空湍流
1999年10月17日中午一架由昆明飞往香港的南方 航空公司的班机在香港上空突然遇到一股强大气流 ，在5至10秒内飞机急坠2000英尺，导致45人撞向机 舱顶部受伤。导致这场飞行事故的“罪魁祸首” 就 是人称飞机的“隐形杀手”－晴空湍流。
一般来说，飞机在穿越云层或遇到强大气流时， 会出现颠簸。在万里晴空中，有时也会像平静的海 面下藏有汹涌的暗流一样，偶尔会出现强烈的扰动 气流，使飞机产生剧烈颤簸，航空气象专家称这种 来无影去无踪的气流为晴空湍流。

流体流动现象

流体流动现象

8
层流时的阻力损失—压力降∆p （二） 层流时的阻力损失—压力降 f p1－ p2 = ∆pf 水平等径直管压力降由阻力损失引起。 水平等径直管压力降由阻力损失引起。 层流： 层流： vmax＝2u
d R= 2
p1－p 2 2 ∆pf d 2 2u = v max = R = ( ) 4µl 4µl 2
常用的局部阻力系数的求法 （一）突然扩大
突然扩大时阻力系数 （二）突然缩小
层流时
64 µ 64 λ= = ρ ud Re
层流时λ与 层流时 与 Re 成反比
16
2、量纲分析法 、 流动阻力的影响因素： 流动阻力的影响因素：∆pf＝f(d,l,u,ρ,µ,ε) 变量数n＝ 量纲数r＝ 变量数 ＝7 ，量纲数 ＝3 ， 各因素以幂指数形式表示： 各因素以幂指数形式表示： ∆pf＝a da lb ucρdµeεf 根据量纲一致原则，进行对比求一系列待定系数、指数。 根据量纲一致原则，进行对比求一系列待定系数、指数。 量纲一致原则
5
四、管内流动的分析
（一）层流时的速度分布
1 2
P1
r
F
v
R
P2
1
2
l
对水平等径管内流体进行受力分析， 对水平等径管内流体进行受力分析， 取圆柱形液体柱半径r、长度 ， 取圆柱形液体柱半径 、长度l，
6
层流时轴向受力如下： 层流时轴向受力如下： 面1－1的总压力 P1=πr2p1
dv F = 2π rl µ dr
1 = 2 lg d + 1.14
λ
ε
使用范围广， 使用范围广，需试差
20
2.粗糙管 粗糙管 顾毓珍等公式
λ =0.01227+

5.流体流动现象

5.流体流动现象
流体流动现象
叶宏
2012-6-13
1
主要内容
• • • • • • 牛顿粘性定律 流体流动的内摩擦力 流动类型 圆管内的速度分布 边界层与边界层分离 小结
2012-6-13
2
一、 牛顿粘性定律
流体在园管中截面上各 点的流速并不相同，而 是存在流速分布。如右 图所示。
u
影响流体流动时内摩擦大小的因素很多， 属于流体物理性质方面的因素是流体的粘 度。 粘度是衡量流体粘性大小的物理量。
流动的阻力发生 在边界层内
2012-6-13 28
x
边界层理论
二、边界层的形成过程 （一）绕平板流动的边界层 1.绕平板流动的边界层的形成
分界面
u=0.99u0
边界层 的厚度
δ
x
粘性底层
x
2012-6-13
随着x增大，边界层不断增厚
29
边界层理论
1.绕平板流动的边界层的形成
层流边界层 过渡区 湍流边界层 速度梯度减小，粘性力下 降，扰动迅速发展
2 r 1 R
即流体在圆形直管内层流流动时，其速度呈抛物线分布。
管截面上的平均速度
u VS A

R .
u 2 rdr
0
R
2

1 2
u max
2012-6-13
即层流流动时的平均速度为管中 心最大速度的1/2。
24
2. 湍流的速度分布 由于湍流运动十分 复杂，尚未从理论 上导出管内的速度 分布式，一般采用 经验公式。（右图 为书上图1-17）

du dy
流动边界层内特别是层流底层内，集中了绝大部分的传递 阻力。因此，尽管边界层厚度很小，但对于研究流体的流 动阻力、传热速率和传质速率有着非常重要的意义。

流体力学现象

流体力学现象

流体力学现象
流体力学是研究流体的力学性质、流动规律及其应用的学科。

以下是一些常见的流体力学现象：
1.粘性：液体和气体都具有粘性，即流体的分子之间有一定的吸引力和相互作用，导致在流动过程中有摩擦力产生。

2.层流和湍流：流体在管道或其它空间中流动时，会产生两种不同的流动方式，即层流和湍流。

层流是指流体在管道内呈现出非常规律的流动模式，而湍流则是指流体在管道内呈现出非常不规律的流动模式。

3.空气动力学：空气动力学是研究空气流动的力学学科，包括研究空气在物体表面流动时产生的阻力、升力等现象。

4.热对流：在浮力的作用下，热气体或热液体会通过对流方式传热。

这是一种非常常见的现象，常见于地球的自然界中，例如大气环流和海洋环流等。

5.水波和声波：当水流或者空气流动时，会形成一种波形的运动。

当这种运动以某种特定的频率振动时，会产生一种水波或声波的现象。

6.流体静力学：研究静止流体的力学特性，包括研究容器中的液体或气体受力、流体中的压力分布等。

7.表面张力：当流体与其他物质接触时，流体表面会呈现一种张力的状态，这种现象被称为表面张力。

例如水鸟在水面上滑行时所形成的水滑翔现象就是一种表面张力的作用。

化工原理知识点总结复习重点(完美版)

化工原理知识点总结复习重点(完美版)

第一章、流体流动一、 流体静力学 二、 流体动力学 三、 流体流动现象四、流动阻力、复杂管路、流量计一、流体静力学：● 压力的表征：静止流体中，在某一点单位面积上所受的压力，称为静压力，简称压力，俗称压强。

表压强（力）＝绝对压强（力）-大气压强（力） 真空度＝大气压强-绝对压大气压力、绝对压力、表压力（或真空度）之间的关系 ● 流体静力学方程式及应用：压力形式 )(2112z z g p p -+=ρ 备注：1)在静止的、连续的同一液体内，处于同一 能量形式g z p g z p 2211+=+ρρ水平面上各点压力都相等。

此方程式只适用于静止的连通着的同一种连续的流体。

应用：U 型压差计 gR p p )(021ρρ-=- 倾斜液柱压差计微差压差计二、流体动力学● 流量质量流量 m S kg/sm S =V S ρ体积流量 V S m 3/s质量流速 G kg/m 2s(平均)流速 u m/s G=u ρ ● 连续性方程及重要引论：22112)(d d u u = ● 一实际流体的柏努利方程及应用（例题作业题） 以单位质量流体为基准：f e W pu g z W p u g z ∑+++=+++ρρ222212112121 J/kg 以单位重量流体为基准：f e h gp u g z H g p u g z ∑+++=+++ρρ222212112121 J/N=m 输送机械的有效功率： e s e W m N = 输送机械的轴功率： ηeN N =（运算效率进行简单数学变换）应用解题要点：1、 作图与确定衡算范围:指明流体流动方向，定出上、下游界面；2、 截面的选取：两截面均应与流动方向垂直；3、 基准水平面的选取：任意选取，必须与地面平行，用于确定流体位能的大小；4、 两截面上的压力：单位一致、表示方法一致；5、 单位必须一致：有关物理量的单位必须一致相匹配。

三、流体流动现象：流体流动类型及雷诺准数：（1）层流区 Re<2000 （2）过渡区 2000< Re<4000 （3）湍流区 Re>4000本质区别：（质点运动及能量损失区别）层流与端流的区分不仅在于各有不同的Re 值，更重要的是两种流型的质点运动方式有本质区别。

化工原理之一 流体流动

化工原理之一 流体流动

第一章: 流体流动流体流动是化工厂中最基本的现象。

在化工厂内，不论是待加工的原料或是已制成的产品，常以液态或气态存在。

各种工艺生产过程中，往往需要将液体或气体输送至设备内进行物理处理或化学反应，这就涉及到选用什么型式、多大功率的输送机械，如何确定管道直径及如何控制物料的流量、压强、温度等参数以保证操作或反应能正常进行，这些问题都与流体流动密切相关。

流体是液体和气体的统称。

流体具有流动性，其形状随容器的形状而变化。

液体有一定的液面，气体则否。

液体几乎不具压缩性，受热时体积膨胀的不显著，所以一般将液体视为不可压缩的流体。

与此相反，气体的压缩民很强，受热时体积膨胀很大，所以气体是可压缩的流体。

如果在操作过程中，气体的温度和压强改变很小，气体也可近似地按不可压缩流体来处理。

流体是由大量的不断作不规则运动的分子组成，各个分子之以及分子内部的原子之间均保留着一定的空隙，所以流体内部是不连续而存在空隙的，要从单个分子运动出发来研究整个流体平衡或运动的规律，是很困难而不现实。

所以在流体力学中，不研究个别分子的运动，只研究由大量分子组成的分子集团，设想整个流体由无数个分子集团组成，每个分子集团称为“质点”。

质点的大小与它所处的空间在、相比是微不足道的，但比分子自由程要大得多。

这样可以设想在流体的内部各个质点相互紧挨着，它们之间没有任何空隙而成为连续体。

用这种处理方法就可以不研究分子间的相互作用以及复杂的分子运动，主要研究流体的宏观运动规律，而把流体模化为连续介质，但不是所有情况都是如此的，高真空度下的气体就不能视为连续介质了。

液体和气体统称为流体。

流体的特征是具有流动性，即其抗剪和抗张的能力很小；无固定形状，随容器的状而变化；在外力作用下其内部发生相对运动。

化工生产的原料及产品大多数是流体。

在化工生产中，有以下几个主要方面经常要应用流体流动的基本原理及其流动规律：(1) 管内适宜流速、管径及输送设备的选定；(2) 压强、流速和流量的测量；(3) 传热、传质等过程中适宜的流动条件的确定及设备的强化。

管内流体流动现象

管内流体流动现象

剪应力可写为以下形式
F ma m du d (mu ) τ= = = = A A A dθ Adθ
式中： 式中： 为时间； （mu）为动量，θ为时间； ）为动量， 为时间
所以剪应力表示了单位时间、 所以剪应力表示了单位时间 、 通过单位 面积的动量， 即动量通量， 面积的动量 ， 即动量通量 ， 牛顿粘性定律也 反映了动量通量的大小。 反映了动量通量的大小。
d u µ d ( ρu ) d ( ρu ) = =ν τ =µ dy ρ dy dy
式中： 式中：
.
.
.
.
（1-31b） ）
ρu =
.
mu V
.
——为单位体积流体的动量，称 为单位体积流体的动量， 为单位体积流体的动量 为动量浓度； 为动量浓度； ——为动量浓度梯度。 为动量浓度梯度。 为动量浓度梯度
二、流型判据——雷诺准数 流型判据 雷诺准数
1.流体的流动类型可用雷诺数 判断 流体的流动类型可用雷诺数Re判断 流体的流动类型可用雷诺数
Re =
dρu
µ
（1-33） ）
Re准数是一个无因次的数群。 准数是一个无因次的数群。 准数是一个无因次的数群
2.判断流型： 判断流型： 判断流型 大量的实验结果表明，流体在直管内流动时： 大量的实验结果表明，流体在直管内流动时： Re≤2000时，流动为层流，此区称为层流区； 时 流动为层流，此区称为层流区； Re≥4000时，一般出现湍流，此区称为湍流区； 时 一般出现湍流，此区称为湍流区； 2000< Re <4000 时，流动可能是层流，也可能 流动可能是层流， 是湍流，该区称为不稳定的过渡区。 是湍流，该区称为不稳定的过渡区。
如图所示，设有上、下两块面积很大且相距 如图所示，设有上、 很近的平行平板，板间充满某种静止液体。 很近的平行平板，板间充满某种静止液体。 若将下板固定， 若将下板固定 ， 而对上板施加一个恒定的外 上板就以恒定速度u沿 方向运动 方向运动。 力，上板就以恒定速度 沿x方向运动。 较小， 若u较小，则两板间的液体就会分成无数平行 较小 的薄层而运动， 的薄层而运动 ， 粘附在上板底面下的一薄层流体 以速度u随上板运动 随上板运动， 以速度 随上板运动， 其下各层液体的速度 依次降低， 依次降低 ， 紧贴在下 板表面的一层液体， 板表面的一层液体 ， 因粘附在静止的下板 其速度为零， 上, 其速度为零，两平 板间流速呈线性变化。 板间流速呈线性变化 。

流体的微重力环境下的流动现象

流体的微重力环境下的流动现象

流体的微重力环境下的流动现象微重力环境下的流动现象是指在低重力或零重力状态下，流体的流动特性和行为。

这种环境可能出现在航天飞行器中、太空站以及一些实验室内。

微重力环境下的流动现象具有独特的特点和挑战，对于理解流体力学和应用于空间科学和工程中具有重要意义。

1. 经典流体力学模型在微重力环境下的适用性经典流体力学模型是基于重力场的，因此在微重力环境下其适用性受到限制。

例如，在微重力环境下，流体无法产生自然对流，这种现象主要是由于缺乏重力驱动机制。

因此，传统的对流换热模型需要进行调整和重新设计。

2. 表面张力对微重力环境下流动的影响在微重力环境中，表面张力开始起主导作用。

表面张力是液体表面处具有的分子吸引力所引起的现象。

在地球上，由于重力的作用，液体流动时会产生靠近容器壁面的附着层，而微重力环境下，表面张力支配的流体流动更加复杂。

3. 液滴行为在微重力环境下的研究微重力环境为研究液滴行为提供了一个独特的实验平台。

在微重力环境下，液滴的形状和稳定性受到表面张力的影响。

研究发现，液滴在微重力环境下会变得更加圆滑和稳定，且难以与周围环境发生相互作用。

4. 混合和传质过程的改变微重力环境下的混合和传质过程与地球上的流体行为存在明显差异。

由于无重力状态下流体的对流受到限制，传质主要通过扩散来实现。

因此，在微重力环境下，理解和掌握传质机制对于航天科学和技术领域至关重要。

5. 微重力环境下的流动控制和应用在微重力环境下，流动控制和应用具有重要的研究价值和应用前景。

例如，通过优化微重力环境下的流体流动，可以实现有效的热管散热系统、微重力实验室中的样品处理以及微重力生物科学实验中液滴的操作等。

总结：流体的微重力环境下的流动现象是一个重要的研究领域，对于航天科学和工程领域具有重要的理论和实际应用价值。

在微重力环境下，经典流体力学模型的适用性受到限制，表面张力、液滴行为、混合传质以及流动控制和应用等方面的研究成果对于解决微重力环境下流体流动的诸多问题具有重要意义。

第三节流体的流动现象

第三节流体的流动现象

第三节流体的流动现象Fluid-flow Phenomena化工生产中的许多过程都与流体的流动现象密切相关，流动现象是个极为复杂的问题，涉及面广，本节只作简要的介绍。

3-1 牛顿粘性定律与流体的粘度一、牛顿粘性定律流体具有两个特性：（1）流动性：即没有固定形状，在外力作用下其内部产生相对运动。

（2）粘性：即在运动的状态下，流体还有一种抗拒内在的向前运动的特性，粘性是流动性的反面。

以水在管内流动时为例，管内任一截面上各点的速度并不相同，中心处的速度最大，愈靠近管壁速度愈小，在管壁处水的质点附于管壁上，其速度为零，其他流体在管内流动时也有类似的规律。

所以，流体在圆管内流动时，实际上是被分割成无数极薄的圆筒层，一层套着一层，各层以不同的速度向前运动，如图1-10所示。

由于各层速度不同，层与层之间发生了相对运动，速度快的流体层对与之相邻的速度较慢的流体层发生了一个推动其向前运动方向前进的力，而同时速度慢的流体层对速度快的流体层也作用着一个大小相等，方向相反的力，从而阻碍较快的流体层向前运动。

这种运动着的流体内部相邻两流体层间的相互作用力，称为流体的内摩擦力，是流体粘性的表现，所以又称为粘滞力或粘性摩擦力。

流体在流动时的内摩擦，是流动阻力产生的依据，流体流动时必须克服内摩擦力而作功，从而将流体的一部分机械能转变为热而损失掉。

流体流动时的内摩擦力大小与哪些因素有关?可通过下面情况加以说明。

如图1-11所示，设有上下两块平行放置且面积很大而相距很近的平板，板间充满了某种液体。

若将下板固定，而对上板施加一个恒定的外力，上板就以恒定的速度u沿x方向运动。

图10流体在圆管内分层流动示意图此时，两板间的液体就会分成无数平行的薄层而运动?粘附在上板底面的一薄层液体也以速度u随上板而运动，其下各层液体的速度依次降低，粘附在下板表面的液层速度为零。

实验证明，对于一定的液体，内摩擦力F与两流体层的速度差Δu成正比，与两层之间的垂直距离Δy 成反比；与两层间的接触面积S 成正比，，即：S yu F ∆∆∝ 若把上式写成等式，就需引进—个比例系数μ即：S yu F ∆∆=μ 式中的内摩擦力F 与作用面S 平行。

流体流动2

流体流动2
对不可压缩流体（液体）， ρ =常数 则： A1u1 = A2u2 or: u1 A2 u2 A 1 对圆形管道
二、讨论：
1.
2.
则：
u1 d2 2 u2 d1
2
第四节 质量、能量和动量衡算（5）
3-2-2
流体流动时的物料衡算—连续性方程
二、讨论：
结论：（1）液体在沿着管道作定态流动时，
其流速与管道的截面积有关；
第四节 质量、能量和动量衡算（16）
3-2-3
机械能衡算—柏努利方程
３ -３ )
三、求静压力（求p ）（p106
第四节 质量、能量和动量衡算（16）
3-2-3
机械能衡算—柏努利方程
例3-4）
四、确定泵的功率（求He ）:
例4：（书P107
1.速度的计算 2.功率
第四节 质量、能量和动量衡算（16）
？
1.流动过程中为什么会消耗能量，
产生阻力 h ？
f
2.流体在管内如何运动？
3.
hf
如何计算？
粘度（书
hf
3-1-5）
阻力
摩擦
粘性
所以：产生阻力的原因：粘性
粘度（书
1.举例：
3-1-5）
一、牛顿粘性定律与流体的粘度
（1）倒水与倒油的感觉 （2）木棒插入空气、水、甘油中的感觉
结论：倒水比倒由快；气体比液体快
3-３
流体压力和流量的测量
3.3.1 压力的测量（p108-109）
3.3.2 流量的测量（p109-110）
3-4
管内流体流动的阻力
3.4.1 管、管件和阀门（p113-115）
第三节
3-4-2

流体流动现象

流体流动现象

2. 湍流分布
r⎞ ⎛ 由实验得到： uz = umax ⎜ 1 − ⎟ R⎠ ⎝
1 n
其中：
n～Re n=6 n=7 n=10
图1-25 湍流时的速度分布
4×104<Re<1.1×105 1.1×105<Re<3.2×106 Re>3.2×106
umax
u'
对于化工过程流体流动，通常取 n=7 即：
⎡ τ ⎤ N m2 N ⋅ s [μ ] = ⎢ ⎥ = m s = m 2 = Pa ⋅ s ⎣ du dy ⎦ m
1 Pa ⋅ s = 10 P = 1000cP
1 P = 100cP
获取方法：属物性之一，
由实验测定、查有关手册或资料、用经验公式计算。
影响因素： 主要有体系、温度、浓度
T ↑, μ L ↓, μ G ↑
qv = 2πumax ∫
R
0
⎛ r2 ⎞ r ⎜ 1 − 2 ⎟dr ⎜ R ⎟ ⎝ ⎠
1 qv = 2 πR2umax
1 u = umax 2
（2） 湍流流动
r⎞ ⎛ uz = umax ⎜ 1 − ⎟ R⎠ ⎝
1 n
qv = ∫ 2πruz dr
R 0
图1-25 湍流时的速度分布
qv = 2π umax ∫
( )
τr =ε
d ρ ux dy
( )
τ r：涡流应力或涡流动量通量，N/m2。
ε：涡流运动黏度或涡流动量扩散系数，m2/s。 涡流动量通量=涡流动量扩散系数×时均动量浓度梯度 总动量：
τ t = τ + τ r = (ν + ε )
d ρ ux dy
( )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由此例可见,无论采用何种单位制来计算,Re值都相等.
[例1-17]在 得无缝钢管中输送燃料油,油得运动粘度为90cSt,试求燃料油坐标滞流流动时得临界速度.
解:由于运动粘度 ,则 .滞流时,Re得临界值为2000,即
Re=du/v=2000
式中d=168-5x2=158mm=0.158m
(1—30)
图1－14中b、c、d曲线所代表的流体，其表观粘度凡都只随剪切速率而变，和剪切力作用持续的时间无关，故称为与时间无关的粘性流体，又可分为下面三种。
1)假塑性(Pseudoplastic)流体这种流体的表观粘度随剪切速率的增大而减小，τ对γ的关系为一向下弯的曲线，该曲线可用指数方程来表示：
τ=τ0+η0 (1—32)
式中τ0—屈服应力，Pa；
η0—刚性系数，Pa·s。
二、与时间有关的粘性流体.
在一定剪切速率下，表观粘度随剪切力作用时间的延长而降低或升高的流体，则为与时间有关的粘性流体。它可分为下面两种。
1)触变性(thixotropic)流体这种流体的表观粘度随剪切力作用时间的延长而降低，属于此类流体的如某些高聚物溶液、某些食品和油漆等。
[例1-16]20℃得水在内径为50mm得管内流动,流速为2m/s.试分别用法定单位制和物理单位制计算准数得数值.
解:(1)用法定单位制计算从本教材附录六查得水在20℃时
已知:管径d=0.05m,流速u=2m/s,则
Re=
(2)用物理单位制计算
u=2m/s=200cm/s, d=5cm
所以Re=99320
(1—26a)
式中 —速度梯度，即在与流动方向相垂直的y方向上流体速度的变化率；
—比例系数，其值随流体不同而异，流体的粘性愈大，其值愈大，所以称为粘滞系数或动力粘度，简称为粘度
式1—26或式1—26a所显示的关系，称为牛顿粘性定律。
图1—13—般速度分布示意图
二、流体的粘度
式1—26a可改写成
所以粘度的物理意义是促使流体流动产生单位速度梯度的剪应力。由上式可知，速度梯度最大之处剪应力亦最大，速度梯度为零之处剪应力亦为零。粘度总是与速度梯度相联系，只有在运动时才显现出来。分析静止流体的规律时就不用考虑粘度这个因素。
涨塑性流体比假塑性流体少得多，如玉米粉、糖溶液、湿沙和某些高浓度的粉末悬浮液等均属此类流体。
3)宾汉塑性(Binghamplastic)流体这种流体的τ-γ关系如图1—14的直线d所示，它的斜率固定，但不通过原点，该线的截距τ0称为屈服应力。这种流体的特性是，当剪应力超过屈服应力之后才开始流动，开始流动之后其性能像牛顿型流体一样。属于此类的流体有纸浆、牙膏和肥皂等也塑性流体的流变特性可表示为
1—3—2非牛顿型流体
服从牛顿粘性定律的流体，称为牛顿型流体，所有气体和大多数液体都属于这一类。
由前已知，牛顿粘性定律的表达式为
(1 -26a)
根据速度的定义，可将速度梯度改写为
上式中dx／dy表示剪切程度的大小， 即为剪切速率，以γ表示，于是牛顿粘性定律可改写为
(1—26b)
上式称为流变方程，在直角坐标图上标绘τ对du／dy(或τ)的关系，可得一条通过原点的直线，如图1—14中的a线所示。该图称为流变图。
(泊)
[例1—15]从某手册中查得水在40oC时的粘度为0.656cP(厘泊)，试换算成Pa·s单位。
解：lcP=0.01P=0.01
或1Pa·s=1000cP
则0.656cP=65.6X10-5Pa·s
此外，流体的粘性还可用粘度μ与密度ρ的比值来表示。这个比值称为运动粘度，以γ表示，即
γ= (1—27)
流体流动时的内摩擦力大小与哪些因素有关?可通过下面情况加以说明。
图1—11流体在圆管内分层流动示意图
图1—12平板间液体速度变化图
如图1—12所示，设有上下两块平行放置且面积很大而相距很近的平板，板间充满了某种液体。若将下板固定，对上板施加一个恒定的外力，上板就以恒定的速度u沿x方向运动。此时，两板间的液体就会分成无数平行的薄层而运动，粘附在上板底面的一薄层液体也以速度u随上板运动，其下各层液体的速度依次降低，粘附在下板表面的液层速度为零。
图1—14牛顿流体与非牛顿流体的流变图
a－牛顿型流体b－假塑型流体c－涨塑型流体d－宾汉塑型流体
流体的分类和特性，更多的内容可参阅有关方面的专著。.
根据流体的流变方程式或流变图，可将非牛顿型流体分类如下：
非牛顿型流体
以下按上述分类次序，扼要介绍各种流体。
一、与时间无关的粘性流体
对于与时间无关的粘性流体，在流变图上可见，对du／dy关系曲线或是通过原点的曲线，或是不通过原点的直线，如图1—14中的b、c、d诸线所示。这些关系曲线的斜率是变化的。因此，对与时间无关的粘性流体来说，粘度一词便失去意义。但是，这些关系曲线在任一特定点上也有一定的斜率，故与时间无关的粘性流体在指定的剪切速率下，有一个相应的表观粘度值，即
粘度是流体物理性质之一，其值由实验测定。液体的粘度随温度升高而减小，气体的粘度则随温度升高而增大。压强变化时，液体的粘度基本不变；气体的粘度随压强增加而增加得很少，在一般工程计算中可以忽略，只有在极高或极低的压强下，才需考虑压强对气体粘度的影响。
在法定单位制中，粘度的单位为
某些常用流体的粘度，可以从本教材附录或有关手册中查得，但查到的数据常用其它单位制表示，例如在手册中粘度单位常用cP(厘泊)表示。lcP二0.01P(泊)，P是粘度在物理单位制中的导出单位，即
2)流凝性(Rhexopectic)流体这种流体的表观粘度随剪切力作用时间的延长而增加，此类流体如某些溶胶和石膏悬浮液等。
三、粘弹性(Viscoeltic)流体
此类流体是介于粘性流体和弹性固体之间,它们同时表现出粘性和弹性.在不超过屈服强度的条件下,剪应力除去以后,其变形能部分的复原.属于此种流体的有面粉团,凝固汽油和沥青等.
1-3-3流动类型与雷若准数
为了直接观察流体流动时内部质点的运动情况及各种因素对流动状况的影响,可安排如图1-15所示的实验.这个实验称为雷若实验.在水箱3内装有溢流装置6,以维持水位恒定.箱的底部接一段直径相同的水平玻璃管4,管出口处有阀门5以调节流量.水箱上方装有带颜色液体的小瓶1,有色液体可经过细管2注入玻璃管内.在水流经玻璃管过程中,同时把有色液体送到玻璃管入口以后的管中心位置上.
τ= (1—31)
式中K—稠度系数，Pa·sn；
n—流性指数，无因次。对于假塑性流体，n<1。
大多数与时间无关的粘性流体属于此类型，其中包括聚合物溶液或熔融体、油脂、淀粉悬浮液、蛋黄浆和油漆等。
2)涨塑性(dilatant)流体与假塑性流体相反，这种流体的表观粘度随剪切速率的增大而增加，τ对γ的关系为一向上弯的曲线，如图1—14曲线c所示，该曲线的方程式仍可用式1—31来表示，但式中的n>1。
下标I表示组分的序号。
最后还应指出，在推导柏努利方程式时，曾假设一种理想流体，这种流体在流动时没有摩擦损失，即认为内摩擦力为零，故理想流体的粘度为零。这仅是一种设想，实际上并不存在。因为影响粘度的因素较多，给研究实际流体的运动规律带来很大的困难。因此，为把问题简化，先按理想流体来考虑，找出规律后再加以修正，然后应用于实际流体。而且在某些场合下，粘性并不起主要作用，此时实际流体就可按理想流体来处理。所以，引进理想流体的概念，对解决工程实际问题具有重要意义。
雷若准数的因次为
[Re]=[ ]=
可见,Re准数是一个无因次数群..组成此数群的各物理量,必须用一致的单位表示.因此,无论采用何种单位制,只要数群中各物理量的单位一致,所算出的Re值必相等.
凡是几个有内在关系的物理量按无因次条件组合起来的数群,称为准数或无因次数群.这种组合并非是任意拼凑的,一般都是在大量的实验的基础上,对影响某一现象和过程的各种因素有一定认识后,再用物理分析或数学推演或二者相结合的方法定出来.它既反映所包含的各物理量的内在关系,又能说明某一现象或过程的一些本质.如流体的流动类型,可用雷若数判断.
实验证明，对于一定的液体，内摩擦力F与两流体层的速度差△u成正比；与两层之间的垂直距离△y成反比；与两层间的接触面积S成正例系数 ，即
F=
内摩擦力F与作用面S平行。单位面积上的内摩擦力称为内摩擦应力或剪应力，以 表示，于是上式可写成
(1—26)
式1—26只适用于u与y成直线关系的场合。当流体在管内流动时，径向速度的变化并不是直线关系，而是如图1—13所示的曲线关系，则式1—26应改写成
以水在管内流动为例，管内任一截面上各点的速度并不相同，中心处的速度最大，愈靠近管壁速度愈小，在管壁处水的质点附于管壁上，其速度为零。其它流体在管内流动时也有类似的规律。所以，流体在圆管内流动时，实际上是被分割成无数极薄的圆筒层，一层套着一层，各层以不同的速度向前运动，如图1—11所示。由于各层速度不同，层与层之间发生了相对运动。速度快的流体层对相邻的速度较慢的流体层产生了一个推动其向前进方向的力；同时，速度慢的流体层对速度快的流体层也作用一个大小相等、方向相反的力，从而阻碍较快流体层向前运动。这种运动着的流体内部相邻两流体层间的相互作用力，称为流体的内摩擦力。它是流体粘性的表现，又称为粘滞力或粘性摩擦力。流体流动时的内摩擦，是流动阻力产生的依据，流体流动时必须克服内摩擦力而作功，从而流体的一部分机械能转变为热而损失掉。
实验证明,流体在直管内流动时,当Re≤2000时,流体流动类型属于滞流;当Re≥4000时,流动类型属于紊流;而当Re值在2000~4000的范围内,可能是滞流,也可能是紊流,若受外界条件的影响,如管道直径或方向的改变,外界的轻微的振荡,都易促成紊流的发生,所以将这一范围称为不稳定的过渡区.在生产操作条件下,常将Re>3000的情况按紊流考虑.
图1-15雷若实验装置
1-小瓶2-细管3-水箱4-水平玻璃管5-阀门6-溢流装置