当前位置：文档之家 › 应用光学【第三章】第一部分

应用光学【第三章】第一部分

  • 格式：pdf
  • 大小：1.55 MB
  • 文档页数：53

下载文档原格式

  / 53

合集下载

(应用光学)第三章.眼睛及目视光学系统

(应用光学)第三章.眼睛及目视光学系统

畸变
畸变
畸变是目视光学系统成像的一种 失真现象，表现为图像的几何形 状发生变化。畸变分为桶形畸变
和枕形畸变两种类型。
畸变的测量
畸变的测量通常采用畸变系数， 即实际图像与理想图像的几何形 状差异的比例。畸变系数越大，
畸变越严重。
畸变的影响因素
影响畸变的因素包括光学系统的 设计、镜片质量、制造误差等。
望远镜
用于观察远距离物体的目 视光学系统，通常具有较 大的视场和较长的焦距。
摄影镜头
用于拍摄照片的目视光学 系统，通常具有较高的成 像质量。
目视光学系统的基本参数
焦距
目视光学系统的焦距是指 物镜与目镜之间的距离， 决定了系统的放大倍数和 观察距离。
视场
目视光学系统的视场是指 物镜所能够覆盖的视野范 围，决定了观察者能够看 到的物体范围。
眼镜广泛应用于人们的日常生活和工 作，是矫正视力缺陷、保护眼睛健康 的重要工具。
摄影镜头
摄影镜头是一种将景物光线聚焦在感光材料上的目视光学仪器，能够将景物拍摄 成照片。
摄影镜头广泛应用于新闻报道、广告、电影和摄影等领域，为人们提供了记录和 分享美好瞬间的工具。
04
目视光学系统的性能评价
分辨率
分辨率
对比度
对比度
对比度是衡量目视光学系统区分 明暗变化的能力的指标。对比度 越高，光学系统呈现的图像明暗
差异越大，细节越丰富。
对比度的公式
对比度通常用公式表示为"明暗区 域的亮度比值"。比值越大，对比 度越高。
对比度的影响因素
影响对比度的因素包括光学系统的 透过率、反射率、像差等。优化这 些因素可以提高光学系统的对比度。
分辨率
目视光学系统的分辨率是 指系统能够分辨的最小细 节程度，通常以线对数表 示。

(应用光学)第三章.眼睛及目视光学系统

(应用光学)第三章.眼睛及目视光学系统
应用光学（第四版）
3 人眼及其光学系统
已知显微镜的视放大率为-300，目镜焦距为20mm，求显微镜物镜 的倍率。若人眼的视角分辨率为60’’ ，则用该显微镜能分辨的两物点 的最小距离是多少？
目
250
f目'
=物目
300
物
250 20
物
24
tan 仪 =
y' f目'
物 24
y' y
tan 60''
明视距离: 眼睛前方250mm 距离处，SD=(1 / (-0.25))= -4 近点距离: 眼睛通过调节能看清物体的最短距离. 远点距离: 眼睛能看清物体的最远距离 最大调节范围 = 近点视度 – 远点视度
应用光学（第四版）
3 人眼及其光学系统 不同年龄段正常的人眼调节能力
年龄 10 15 20 25 30 35 40 45 50
'
r'
0.61 n'sin U 'max
0.61 n'(D / 2R)
1.22R n'D
应用光学（第四版）
3 人眼及其光学系统
'
0.61 n'sin U 'max
1.22R n'D
当满足小角度时，sinU'max=tanU'max=U'max
'
0.61 n'sin U 'max
0.61 n’u '
最大调节范围/视度 -14 -12 -10 -7.8 -7.0 -5.5 -4.5 -3.5 -2.5
近点距离 (mm) 70 83 100 130 140 180 220 290 400

《应用光学》第3章 理想像和理想光学系统

《应用光学》第3章 理想像和理想光学系统

n' n n'n
l' l
上式两边同乘以l l'，得
r n'l nl' n'n ll' r
13
上式左边为0，对主点来说，将l'＝n'l / n代入右边得
n'n n' l 2 0 rn
由此得到l＝0，代入nl'＝n'l，又得l'＝0。所以球面
的两个主点H、H'与球面顶点重合。
14
ቤተ መጻሕፍቲ ባይዱ、球面焦距公式 按照球面定义像方焦点为无限远
•n1'= n2= 1.5163; •求: lF, lF', lH, lH', f, f'
采用计算机编程（MATLAB 程序）
22
• 已知条件
• r1=10;r2=-50;d1=5;h1=10;n1=1; • 同理可得：
• n1'=1.5163;n2=n1';
• r2=-10;r2=50;d1=5;h1=10;n1=1;
• 焦距是以相应的主点为原点来确定正负的，如果 由主点到相应焦点的方向与规定光线的正方向相同 为正，反之为负。在图3-1中，f<0 , f '>0. 以后将会 知道 f '>0为正系统，f '<0 为负系统。在图3-1中物 像方平行于光轴的光线高度均为 h，其共轭光线与 光轴的夹角为u和u'，则有：
学系统的物方焦点。显然，根据光路可逆原理，
物方焦点 F 经系统以后必成像于像方无限远的轴 上点。或者说，物方焦点与像方无限远的轴上点 是一对共轭点。
7
过物方焦点 F 的垂轴平面称为物方焦平面。显然，

应用光学(第三章)

应用光学(第三章)

2f ' 2x f' h
h
面反射镜的旋转特性。
Applied Optics
授课：任秀云
平面镜的平移效应
A B
A ′A ″=2h
P
Q
h
A” A’
2h
Applied Optics
授课：任秀云
综上所述， 单个平面镜的成像特性可归纳为：
①具有折转光路的作用，是唯一能成完善像的光学元件 ②β=1,物像虚实相反,具有对称性，故不影响光学系统 放大率和成像清晰度。 ③奇数次反射成镜像， 偶数次反射成一致像。
Applied Optics
授课：任秀云
这种系统就是原始的军用观察望远镜的光学系统，其体积、重 量都比较大，不能满足军用观察望远镜的要求，故早已被淘汰 了。目前使用的军用观察望远镜，由于在系统中使用了棱镜， 如图(b)所示，所以它不需要加入倒像透镜组即可获得正像，同 时又可大大地缩小仪器的体积和重量。
Applied Optics
授课：任秀云
此外，在很多仪器中，根据实际使用的要求，往往需要 改变共轴系统光轴的位置和方向。例如在迫击炮瞄准镜 中，为了观察方便，需要使光轴倾斜一定的角度，如图 所示：
Applied Optics
授课：任秀云
平面镜棱镜系统主要作用有： (1)将共轴系统折叠以缩小仪器的体积和减轻仪器 的重量； (2)改变像的方向——起倒像使用； (3)改变共轴系统中光轴的位置和方向——即形成 潜望高或使光轴转一定的角度； (4)利用平面镜或棱镜的旋转，可连续改变系统光 轴的方向，以扩大观察范围。 (5)利用平面镜转动作用扩大仪器的放大率 (6)实现分光、合像和微位移
3、当角锥棱镜绕其顶点旋转 时，出射方向不变仅产生一 个平移。

应用光学【第三章】习题第一部分

应用光学【第三章】习题第一部分

1.200倍显微镜的目镜焦距为25mm, 求显微镜目镜视放大率和物镜
垂轴放大率。

2.对正常人眼，如要观察2m远的目标，需要调节多少视度？
3.已知显微镜的视放大率为-300，目镜的焦距为20mm，求显微镜物
镜的倍率。

假定人眼的视角分辨率为60”，问使用该显微镜观察时，能分辨的两物点的最小距离等于多少？
4.用一架5倍的开普勒望远镜，通过一个观察窗观察位于距离
500mm远处的目标，假定该望远镜的物镜和目镜之间有足够的调焦可能，该望远镜物镜的像方焦距为100mm，求此时仪器实际视放大率等于多少？。

应用光学实验-TUTE

应用光学实验-TUTE

应用光学实验第一部分基础型实验实验1 光组的成像特性一、实验目的1.验证物像位置关系，深入了解透镜成像特性。

2.掌握望远镜、显微镜、复合透镜的组合方法。

3.观察光线在棱镜中传播的情况，并了解各种棱镜的成像特性，熟悉各种棱镜的结构。

二. 实验仪器设备1.六只正透镜、二只负透镜、光具座、一只平行光管、平面反射镜、投影屏。

2.指标、透镜架、透镜、成像屏、光具座、照明系统。

3.在平行光管物镜的物方焦平面上置一块带指标的分划板，分划板通过物镜成像于无穷远，即可在实验室条件下提供“无穷远物体”。

三.实验原理及要求1.实验原理：l和l’分别表示物像距，f’为光组的焦距，则当光组处于空气中时，有：可知，对于具有一定焦距的光组，其像的位置随物体位置的变化而变化，而其相应的横向放大率可表示如下：2. 实验要求取一正透镜使物体（指标）位于①②③④；取一负透镜使物体位于①②③④，分别记录物体经透镜所成像的大小、正倒及位置。

①组合4倍的开普勒望远镜，目镜焦距50mm。

②组合4倍的伽利略望远镜，目镜焦距-50mm。

③组合一显微镜，放大倍率为15倍，目镜焦距为50mm，物镜的共轭距为180mm。

④有限焦距物镜与望远镜的组合（开普勒望远镜）。

⑤二块正、负透镜在间距不变的条件下交换它们的前后位置，分别构成二组组合物镜（）。

⑥观察二个正透镜的组合焦距随间隔的变化规律。

四. 实验任务1.用一块焦距为200mm的正透镜，放在十字物体前，取一块平面反射镜置于透镜前，这时在十字物体旁有一反射像，然后改变透镜和物体之间距离直至反射像清晰，并且物像大小相等，这说明物体已位于透镜的焦平面上，射出平行光，这就在实验室条件下提供了“无穷远物体”，这种方法叫自准直法。

2.组合4倍的开普勒望远镜，先计算出当时物镜的焦距，然后用自准直法使物镜的像方焦点和目镜的物方焦点相重合，即为开氏望远镜。

3.有限焦距物镜与望远镜的组合（开普勒望远镜），在以上组成的开普勒望远镜系统前、后放一块已知焦距的透镜，然后分析放在前后位置的不同情况。

国科大应用光学作业答案_1-7_

国科大应用光学作业答案_1-7_

1、根据费马原理证明反射定律。

答案：略2、某国产玻璃的n C=1.51389, n d=1.5163, n F=1.52195，计算其阿贝数，并查出该玻璃的牌号。

答案：V=64.06、K93、求图1-5的入射角i1。

答案：25.81︒4、已知入射光线A的三个方向余弦为cosα、cosβ、cosγ，反射光线A'的三个方向余弦为cosα'、cosβ'、cosγ'，求法线方向。

答案：cosα'-cosα、cosβ'-cosβ、cosγ'-cosγ5、有一光线o o=+A i j入射于n=1和n'=1.5的平面分界面上，平面cos60cos30的法线为o oN i j，求反射光线A'和折射光线A''。

cos30cos60=+答案：略6、有一光线以60︒的入射角入射于n=点反射和折射的光线间的夹角。

答案：90︒7、在水中深度为y处有一发光点Q，作QO面垂直于水面，求射出水面折射线的延长线与QO交点Q '的深度y'与入射角i的关系。

答案：'y=1、一个玻璃球直径为400mm，玻璃折射率为1.5。

球中有两个小气泡，一个在球心，一个在1/2半径处。

沿两气泡连线方向，在球的两侧观察这两个气泡，它们应在什么位置？如在水中观察(水的折射率为1.33)时，它们又应在什么位置？答案：空气中：80mm、200mm；400mm、200mm水中：93.99mm、200mm；320.48mm、200mm2、一个折射面r=150mm, n=1, n'=1.5，当物距l=∞, -1000mm, -100mm, 0, 100mm, 150mm, 1000mm时，横向放大率各为多少？答案：0、-3/7、3/2、1、3/4、2/3、3/133、一个玻璃球直径为60mm，玻璃折射率为1.5，一束平行光射到玻璃球上，其汇聚点在何处？答案：l'=15mm4、一玻璃棒(n=1.5)，长500mm，两端面为凸的半球面，半径分别为r1=50mm, r2= -100mm，两球心位于玻璃棒的中心轴线上。

应用光学第3章 理想光学系统

应用光学第3章 理想光学系统
2.设一焦距为50mm的负透镜在空气中，在其前 面设置一高度为50mm的物于 4f,3f,2f和 1 .5f 处。请分别用高斯公式和牛顿公式求其像的 位置和大小。
3.设一焦距为30mm的负透镜在空气中，在其后 面0.5f,1.5f,2.5f和 3.5f处分别置一高度为 60mm的虚物，请分别用高斯公式和牛顿公式 求其像的位置和轴向放大率。
y f
yx
三角形A’B’F’和三角形H’N’F’相似
，得：
y x
y f
xxff
————此式即为牛顿公式。
二、高斯公式
以物、像方主点为原点来确定物和像的位置。 物距：物方主点到物点的距离，用l表示。 像距：像方主点到像点的距离，用l'表示。
高斯公式：
x=l- f
x′ =l′ - f′
应用光学第3章 理想光学系统
教学目标
掌握理想光学系统的物像关系、基点和基 面。
牢固掌握解析法和图解法求像的方法。 牢固掌握理想光学系统的双光组组合和透
镜的焦距、基点（基面）。 理解多光组组合的焦距计算公式。 了解各种厚透镜的基点、基面位置。 掌握望远系统的成像特性。
引言
研究近轴光学的实际意义
依据： ①平行于光轴的光线经理想光学系统后必过像方焦点
②过物方焦点的光线经理想光学系统后必为平行于光 轴的光线；
由物方无限远射来的任何方向的平行光束，经光学 系统后会聚于像方焦平面上一点。
过F’点作垂直于光轴的平面，称为像方焦平面（或 后焦平面,或第一焦面）。
物方焦平面是像方无限远垂轴平面的共轭像面。
由光学系统物方焦平面上任一点发出的光束，经光 学系统后平行出射。
总结：
像方焦点和物方无限远轴上点是一对共轭点； 物方焦点和像方无限远轴上点是一对共轭点； 像方焦面和物方无限远垂轴平面是一对共轭面； 物方焦面和像方无限远垂轴平面是一对共轭面。

应用光学【第三章】第一部分（ＰＤＦ）

应用光学【第三章】第一部分（ＰＤＦ）

第三章光学仪器目视光学仪器：和人眼配合使用的仪器本章主要解决的问题：•眼睛的构造•望远镜、显微镜的工作原理•眼睛与目视光学仪器配合的问题、眼睛缺陷及调整•如何选择成像光束的位置•选择成像光束的原则•限制光束的方法§3-1人眼的光学特性•人眼的构造从光学角度看，主要有三部分：－－－－镜头－－－－底片－－－－光阑人眼相当于一架照相机，能够自动调节角膜：透明球面，光线首先通过角膜进入眼睛前室：角膜后面的空间部分，充满水液，n=1.3374,对光线起会聚作用水晶体：双凸透镜，借助周围肌肉的收缩及松弛，前表面半径可减小或加大，改变焦距。

角膜，前室和水晶体相当于镜头部分。

视网膜：视神经细胞和神经纤维，相当于感光底片黄斑：视网膜上视觉最灵敏的地方这两项相当于感光部分虹膜：水晶体前面的薄膜，中心有一圆孔，成为瞳孔，随着入射光能量的多少，瞳孔直径可放大或缩小。

相当于可变光阑盲点：视神经纤维的出口，没有感光细胞，不产生视觉盲点实验视觉的产生外界的光线进入人眼成像在视网膜上，产生视神经脉冲通过视神经传向大脑，经过高级的中枢神经活动，形成视觉物理过程，生理过程，心理过程人眼的光学特性视轴：黄斑中心与眼睛光学系统的像方节点连线人眼视场：观察范围可达150º头不动，能看清视轴中心6º－8º要看清旁边物体，眼睛在眼窝内转动，头也动人眼的调节：视度调节、瞳孔调节1、视度调节定义：随着物体距离改变，人眼自动改变焦距，使像落在视网膜上的过程。

F’•调节量的表示：视度与网膜共轭的物面到眼睛的距离的倒数1SD=l 单位为米l•明视距离和近点、远点明视距离：眼睛前方250mm，SD=(1 / (-0.25))= -4 近点：眼睛通过调节能看清物体的最短距离远点：眼睛能看清物体的最远距离最大调节范围＝近点视度－远点视度年龄最大调节范围/视度近点距离/mm10 15 20 25 30 35 40 45 50-14-12-10-7.8-7.0-5.5-4.5-3.5-2.57083100130140180220290400 不同年龄正常人眼的调节能力2、瞳孔调节外界物体的亮暗随物体，天气，时间而不同。

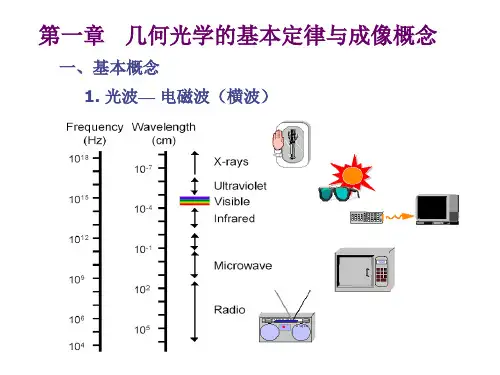
应用光学课件完整版

应用光学课件完整版
由一点A发出的光线经过光学系统后聚交或近似的聚 交在一点A′，则A为物点， A′为物点A通过光学系统 所成的像点。物与象之间的对应关系称为“共轭”。
一个物点，总是发出同心光束，与球面波相对应； 一个像点，理想情况应该由球面波对应的同心光束汇交 而成，称这种像点为完善像点。
3. 成完善象的条件 发光体每一物点发出球面波，通过光学系统后仍为
反射定律可表示为 I I ''
4. 光的折射定律
折射定律可归结为：入射光线、折射光线和投射点
的法线三者在同一平面内，入射角的正弦与折射角正弦
之比与入射角大小无关，而与两介质性质有关。对一定 波长的光线，在一定温度和压力的条件下，该比值为一
常数，等于折射光线所在介质的折射率与入射光线所在
介质折射率之比。
0 i arcsin n12 n2 2 n0
n0 ＝1
n0 sin i n1 cos ic n12 n22
5. 费马原理（光程极值原理）
1）光程— 光在介质中经过的几何路程l与该介质折射率n的乘积。
s=n • l
均匀介质
m层均匀介质
连续变化的非均匀介质
s=n • l=c • t
m
s
波面可分为：平面波、球面波、任意曲面波。 波面法线方向即为光传播方向。
光源
光线
波面
5. 光束— 与波面对应的法线集合。
同心光束— 波面为球面，聚于一点。 发散光束— 光线在前进方向上无相交趋势。 会聚光束— 光线在前进方向上有相交趋势。
平行光束— 波面为平面。 象散光束— 波面为曲面，不聚于一点。
1. 共轴球面系统的结构参量： 各球面半径：r1 、 r2 …… rk-1 、 rk 相邻球面顶点间隔：d1 、 d2 …… dk-1 各球面间介质折射率：n1 、 n2 …… nk-1 、 nk n 、 k+1

应用光学第三章

应用光学第三章

#
第一节 理想光学系统的共线理论
• 理想光学系统理论又称之为高斯光学，其基本核心 是共线成像。所谓共线成像，就是指在理想光学系 统中的一一对应关系： 1、任一物点在像空间都有一个和它唯一对应的像点； 2、物空间任一条直线，则在像空间也有对应的唯一 直线； 3、物空间任一平面，像空间也有唯一的对应平面。 • 这种点对应点、直线对应直线、平面对应平面的成 像变换即称之共线成像，这种物像一一对应的关系 称之为共轭关系。
M
P A F N H H′ F′ A′ M′ N′
#
1、作图法求像
• 方法二：利用物方平行光线交于后焦面 上一点的性质。
M′ N′ H H′ F F′ A′ P′
M
N A
#
1、作图法求像
• 例题3-4：负光组求像 • 原则上同例题3-2，但要注意，负光组物 像方焦点的位置！
A
A′ H
H′ P′ Q′ F
Q′ H′ Q F′
F
H
#
第二节 理想光学系统的基点与基面
#
第二节 理想光学系统的基点与基面
4、光学系统的焦距
• 焦面到主面的距离定义为光学系统的焦距，像方主点 H′到像方焦点F′的距离称为像方焦距，用f′表示，物方 主点H到物方焦点F的距离称之为物方焦距，用f表示。 由图3-7，有
f ' h 1 h (3-1a） f （3-1b） （3-2） tgU ' f ' tgU
F′
B′ B Q
P
#
1、作图法求像
•例题3-5：虚物求像
M M′
B B′
A′ F′ A
N
H H′ F
N′
#
1、作图法求像

应用光学第三章

应用光学第三章
18
Hale Waihona Puke 三 棱镜的成像方向判断• 基本依据：反射定律 • 对具有单一主截面的系统
设物的坐标为oxyz,为右手坐标系，oz光轴方向，ox在主 截面内的方向，oy垂直于主截面的方向 ①o’z’光轴方向按反射定律定出 ②垂直于主截面的o’y’视屋脊面个数而定，没有或偶数个， 则同向，奇数个，方向 ③主截面内o’x’视反射系统的反射次数而定，奇数次反射 成镜像，偶数次反射物象一致。具体定时，先将光轴方 向定出，然后按是镜像还是相似像按左右手定出
β为两个光楔之间的夹角
当δ1＝δ2＝δ0时，

2
2 0
(1

cos
)

20
cos(
/
2)

2(n
1)
cos(
2
)
光楔是光学系统中对光线小角度偏折的元件，通常一对光楔配 对使用，分别旋转两个光楔，可以使出射光线位于一个以入射 光为轴线的角锥体内的任意方向上
33
几种特殊情况
34
作用：
• 折射棱镜定义
反射棱镜—— 利用表 面的反射作用
折射棱镜 —— 利用表 面的折射作用，工作面 为两个折射面
折射棱 —— 入射面与 出射面的交线
折射角 —— 顶角α
偏向角δ —— 入射光 线与出射光线的夹角从 入射光线转到出射光线， 顺正逆负
α
I1
I1´ n -I2
-I2´ δ
27
2
2
(I1'I2 )]
2
c
os[1 2
(I1

I
2
'
)]
对于给定的棱镜， 和n 为定值，所以由上式可知，偏向角

应用光学教案(第三章)——视光技术应用方向材料科学与工程专业

应用光学教案(第三章)——视光技术应用方向材料科学与工程专业
视力正常的眼睛，近点 距离约为10~12cm。
近视眼及矫正
屈光不正矫正
近点
正常眼近点
远视眼矫正
2
COPYRIGHT 2010 材料工程学院
金陵科技学院材料工程学院
第三章 球面透镜
透镜概述
透镜的概念 由前后两个折射面组成的透明介质称为透镜
（lens），这两个折射面至少有一个是弯曲面。弯曲面可
以为球面、柱面、环曲面或非球面。
15
COPYRIGHT 2005 视光学技术学院
金陵科技学院视光学技术学院
2．凹透镜成像规律
凹透镜所成的像，无 论物体的位置在焦点 以外还是焦点以内， 它经凹透镜折射后， 所成的像，都是缩小 的，正立的虚像。像 和物在透镜的同侧。 因此它的成像规律， 不同于凸透镜那样复 杂。
16
COPYRIGHT 2005 视光学技术学院
11 f2F4.00 0.2m 52c5m
f1F 14 1 .0 0 0.2m 5 2c5m 第二焦点和第一焦点均为实焦点
薄透镜位于空气中时，第二焦点和第一焦点分居透镜的两侧，
且与透镜的距离相等。
f2 f1
例：屈光度为-3.00D凹透镜，其焦距：
n2 n1
f2
f1
f2F 13 1 .0 0 0.3m 3 3 3.3 3 cm
COPYRIGHT
4
视光学技术学院
金陵科技学院材料工程学院
如图3-1-1
5
COPYRIGHT 2005 视光学技术学院
金陵科技学院材料工程学院
6
COPYRIGHT 2005 视光学技术学院
7
8
金陵科技学院材料工程学院
（二）透镜的种类 透镜为凸透镜和凹透镜两种，中央比边缘厚的透镜称为凸透 镜，也称为正透镜、会聚透镜；中央比边缘薄的透镜称为凹 透镜，也称为负透镜、发散透镜。根据凸、凹透镜的前后两 面的形状，透镜可以分为以下六种类型。 1、双凸透镜(bi-convex lens) 2、平凸透镜(plano-convex lens) 3、凸新月形透镜(meniscus- convex lens) 4、双凹透镜(bi-concave lens) 5、平凹透镜(plano-concave lens) 6、凹新月形透镜(meniscus- concave lens)

应用光学 赵存华著 I 1-21章课件

应用光学 赵存华著 I 1-21章课件
I I' I n I n'n I
n' n'
结论: 界面两边折射率差越大偏折光线越大.
n紫 n红
2.6.3 Snell定律的讨论
图2.10 三棱镜分光
2.7 全反射
当 I’=90o, 入射角称 critical angle (临界角). 用Ic表示, 所以有
sin
Ic
n' n
例子: 求光线从水中入射于空气中的全反射临界角
爱里斑的半径为
r0
1.22
2a
f'
3.2.2 理想像的违背
3.3 理想光学系统
光学系统：由反射镜、透镜和棱镜等光学 元件，按一定的方式组合在一起，利用材 料的反射或折射，把入射在其内的光线按 照设计者的要求传递到需要的位置或方向， 从而满足一定需求的系统。
一些概念:
1.共轴系统(coaxal system) 2.光轴(optical axis) 3.非共轴系统(non-coaxal system) 4.球面系统(spheric surface system) 5.非球面系统(aspheric surface system) 6.共轴球面系统(coaxal spheric system) 7.正透镜(positive lens) 8.负透镜(negative lens)
n' 1 n 2
sin I 1 sin I ' 2
nsin I n'sin I'
2.6.3 Snell定律的讨论
讨论:
nsin I n'sin I'
1. 如果 n n' 那么 sin I sin I' 所以 I I '
结论: 折射率小的一边相对法线夹角大.

应用光学第三章 眼睛和目视光学系统

应用光学第三章 眼睛和目视光学系统
等于同一目标用仪器观察时的视角和人眼直接 观察时的视角二者的正切之比，所以称为仪器 的视放大率。
一、放大镜（magnifier）的工作原理
放大镜用来观察近距离微小物体。
物在物方焦点，出射的是平行光束。
人眼直接观察
设一微小物体其高为y，用肉眼直接观察时不能离 眼太近，放在l = -250mm处。此时，视角为：
tan 仪 tan眼
tan1' 4 106
0.0003 4 106
75
3-3 望远镜（telescope）的工作原理
望远镜用来观察无限远的物体
物镜的像方焦点与目镜的物方焦点重合，即光学间隔Δ= 0。
望远镜的视角放大
1. 不用望远镜时，远物对人眼的张角：
眼
2. 通过望远镜后，像对人眼的张角' ：
标放在眼前250mm处，此距离为明视距离。 ✓ 近点距离：人眼通过调节所能看清物体的最短
距离称为近点距离。 ✓ 远点距离：人眼能看清的最远距离。 ✓ 最大调节范围：远点距离与近点距离之间的视
度之差。
二 人眼的调节 -- 视度调节
例：20岁的正常人眼 ✓ 明视距离：250mm，SD = -4。 ✓ 最大调节范围：-10
开普勒望远镜（ fe’ > 0， < 0）
优点：物镜与目镜之间有中间实像，可以安装分划板， 便于瞄准和测量。
缺点：正立的物体成倒像，不方便观察。需加入倒像 系统。
伽利略望远镜（ fe’ < 0， > 0）
优点：正像 缺点：无法安装分划板；另视觉放大率受到物镜口径
的限制，不可能很大，一般在2-3倍。
再经过目镜成像在无限远。
两级放大：
第一级：显微物镜将被观察物体进行尺寸放大； 第二级：靠近眼睛的目镜扩大视角

应用光学第三章

应用光学第三章
y' z'
o
x'
直角棱镜使光线折转90°
等腰棱镜使光线折转任意角度。
二者的特点是：入射面、出射面与光轴垂 直。
道威棱镜，入射面、出射面与光轴不垂 直。
道威棱镜90°旋转后，像旋转180°。
道威棱镜: 绕光轴旋转角，其对应的反射像同 方向2旋转角。
一次反射特点：
成镜像；
在主截面内坐标方向改 变，垂直于光轴截面内坐标方 向不变。
五角棱镜
第二节 平行平板
由两个相互平行的折射平面构成的光学元件
称为平行平面板。
用棱镜来代替平面镜，就相当于在光学系统 中多加了一块平行平面板。 如标尺、刻有标志的分划板、补偿板、滤光 镜、保护玻璃等等 下面讨论光线经过平行平面板的折射情况 假定平行平面板位于空气中
应用折射定律
sin I1 n sin I1'
即物空间为右手坐标
先看几个普通棱镜：
这主要看棱镜的反射次数
偶次反射成一致像，由右手 坐标确定其成像方向；
奇次反射成镜像，由左手坐 标确定其成像方向。
y
（ 一
x
）
一
z
次
y′
反
射
z′
x′
棱

（a）等腰直角棱镜
镜
y x
z
(b)等腰棱镜
x′ z′
y′
y
o
x z
y
o
x z
（c）道威棱镜
o
x' z' y'
把棱镜的光轴截面沿着它 的反射面展开，取消棱镜的 反射，以平行玻璃板的折射 代替棱镜折射的方法称为
“棱镜的展开”
(1).为了使棱镜和共轴球面系统组合后， 仍能保持共轴球面系统的特性，必须对棱 镜的结构提出一定的要求：

应用光学各章知识点归纳

应用光学各章知识点归纳

应用光学各章知识点归纳第一章几何光学基本定律与成像概念波面：某一时刻其振动位相相同的点所构成的等相位面称为波阵面,为光波波阵面的传播，与波面对应的法线束就是光束。

波前：某一瞬间波动所到达的位置。

光线的四个传播定律：11）直线传播定律：在各向冋性的均匀透明介质中，光沿直线传播，相关自然现象有：日月食，小孔成像等。

22）独立传播定律：从不同的光源发出的互相独立的光线以不同方向相交于空间介质中的某点时彼此不影响，各光线独立传播。

33）反射定律：入射光线、法线和反射光线在同一平面内，入射光线和反射光线在法线的两侧，反射角等于入射角。

44）折射定律：入射光线、法线和折射光线在同一平面内；入射光线和折射光线在法线的两侧，入射角和折射角正弦之比等于折射光线所在的介质与入射光线所在的介质的折射率（折射）光线的方向射到媒质表面，必定会逆着原来的入射方向反射（折射）出媒质的性质。

光程：光在介质中传播的几何路程SS和介质折射率nn的乘积。

各向同性介质：光学介质的光学性质不随方向而改变。

各向异性介质：单晶体（双折射现象）马吕斯定律：光束在各向同性的均匀介质中传播时，始终保持着与波面的正交性，并且入射波面与出射波面对应点之间的光程均为定值。

全反射临界角：C=arcin全反射条件：11）光线从光密介质向光疏介质入射。

22）入射角大于临界角。

共轴光学系统：光学系统中各个光学兀件表面曲率中心在一条直线上。

物点//像点：物//像光束的交点。

实物//实像点：实际光线的汇聚点。

虚物//虚像点：由光线延长线构成的成像点。

共轭：物经过光学系统后与像的对应关系。

（AA,A"的对称性）完善成像：任何一个物点发出的全部光线，通过光学系统后，仍然聚交于同一点。

每一个物之比，即inIinIn"n简称波面。

光的传播即光路可逆：光沿着原来的反射费马原理：光总是沿光程为极小，极大，或常量的路径传播。

n2ni点都对应唯一的像点。

理想成像条件：物点和像点之间所有光线为等光程。

应用光学第二版胡玉禧课件第3章

应用光学第二版胡玉禧课件第3章

r = ∞
l ' = −l
即像与物相对于平面镜来说是对称的。(性质1）
第三章 平面零件成像
②放大率公式：
即物像大小一致，且成正像。但左右相反。（性质2）
第三章 平面零件成像
3、镜像与一致像 1）所谓镜像是指物体经平面反射镜成像时，像和物大小 相等形状不同，若物为右手坐标，像为左手坐标，这种 像称为镜像。见图3.10 特点：像与物上、下同向，但左右却颠倒，它可通过奇 数次反射得到。 2）一致像：物为右手坐标， y′
I1 I1′ o2 I2 I2′ o1
α
N M
α
图 3.12
β
第三章 平面零件成像
红旗渠最长的隧道——曙 光洞的施工，利用平面反 射镜将太阳光反射照明； 自行车尾灯——偶镜, 三对偶镜构成的角反射器。
第三章 平面零件成像
潜望镜
第三章 平面零件成像
例2.（补充题） 一光学系统由一透镜和平面镜组成，如图。平面镜MM与透 镜光轴交于D点，透镜前方离平面镜600mm处有一问题AB， 经过透镜和平面镜后，所成虚像A"B"至平面镜的距离为 150mm，且像高为物高的一 半，试分析透镜焦距的正 负，确定透镜的位置和焦 距，并画出光路图。
1、术语 ①偏向角：入射光线与出射光线的夹角。 ②折射棱：二个折射面的交线叫棱。 I ③折射角：二个折射面之间的夹角。 ④主截面：垂直于折射棱的平面。 B 2、最小偏向角δm 偏向角公式：
1
δ
C
图 3.2
(3.6)
第三章 平面零件成像
可见，偏向角δ的大小与折射角α、棱镜折射率n、入射角 I1有关，对于某一棱镜而言，其n， α是一定值，此时只有 一个变量就是I1 ，每给一个I1就有一个δ ， I1不同， δ也不 同， 是个变量。称δ为最小值时的这个偏向角为最小偏向 当δ为最小偏向角时，它具有如下特点：即: I1 =- I2′, I1′=- I2, 当将I1 =- I2′, I1′=- I2 , 代入到偏向角公式时，可得到： (3.7) 角 δ m。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
应用光学讲稿
望远镜的放大率
D D'
ห้องสมุดไป่ตู้
1
望远镜的垂轴放大率也不随共轭面的位置变化而变 化，数值上等于视放大率的倒数
测量视放大率的方法：倍率计
应用光学讲稿
§3-4 眼睛的缺陷和目视光学仪器的视度调节
一、眼睛的缺陷和校正
1、正常人眼的焦点F’、远点和近点 正常人眼在自然状态下，无限远物体成像在网膜 上，即焦点F’与网膜重合
应用光学讲稿
望远镜的放大率 tgu ' tg ' tgu tg
望远镜的角放大率不随共轭面的位置变化而变化， 数值上等于视放大率 平行于光轴入射的光线仍然平行于光轴出射 ' y ' f目 f目 1 ' ' y f物 f物
D D'
仪
：用了仪器后目标像对人眼的张角，即像方视场角 ：人眼直接观察时目标对人眼的张角，即物方视场角
眼
仪 '
眼
应用光学讲稿
望远镜的视放大率
tg仪 tg ' tg眼 tg
y tg ' f物
' 1
根据定义有
y2 tg ' ' f目
y y2
' 1
望远镜的视放大率
对两物点的视角分辨率：
两物点在网膜上成两个像点，若两像点距离比较大， 人眼能够分辨开是两个像点，如果两像点距离小到一 定程度，人眼就有可能分辨不出是两个像点。 为什么呢？
应用光学讲稿
人眼视网膜的结构
视网膜由视神经细胞组成，分锥状细胞和杆状细胞
锥状细胞：在亮光下工作
杆状细胞：在弱光下工作
如果两像点之间的距离大于两视神经细胞，落在两 个不相邻视神经细胞上，就能分清是两个像点。
y
β物
y’ -Δ = = y f’物
Г＝
tg ω仪 tg ω眼
=
-250Δ f’物 f’目
应用光学讲稿
目镜
物镜 y’ -y
f’物
F’物
Δ
F目
-f目
ω仪
-Δ
Г＝
f’物
.
250
f’目
＝ β物
.Г
目
应用光学讲稿
物镜的垂轴放大率和目镜的视放大率分别刻在 镜管上，二者相乘，就是显微镜的视放大率。 显微镜的视放大率
y’仪
y’眼
＝
π ’ tg ω仪
π ’ tg ω眼
＝
tg ω仪 tg ω眼
Г越大，放大作用越大。 Г有正负之分， Г为正，正像， Г为负，倒像
应用光学讲稿
• 放大镜工作原理
y
ω －y’
-l
y 物体对人眼张角 tg l ymin 要求最小视角 0.0003弧度(60" ) l
F
-f=f ’
ω仪
－y’
tg ω仪 =
y
f’
tg ω眼 = 250
y
-l
=
y 250
Г＝
tg ω仪 tg ω眼
=
f’
注意：250为明视距离，物体可以移动到明视距离
应用光学讲稿
放大镜的视放大率
250 f'
如果要Γ>1，则要求透镜焦距f’<250mm
要提高放大镜的视放大率，必须减小透 镜的焦距，但对于一个简单的单正透镜，其 焦距不可能很小。
应用光学讲稿
最小视角
ymin 0.0003弧度(60" ) l
提高视角的途径： 提高y，不行。 减小物距L，但不能无限的减小，否 则， 就不能成像在视网膜上。
我们希望物体位在无限远处，因此可以 在人眼前加一个正透镜，把物体放在透 镜的物方焦点处，成像在无限远，供人 眼观察。
应用光学讲稿
远点：眼睛能看清物体的最远距离 最大调节范围＝近点视度－远点视度
应用光学讲稿
不同年龄正常人眼的调节能力 年龄 最大调节范围/视度 近点距离/mm
10 15 20 25 30 35 40 45 50
-14 -12 -10 -7.8 -7.0 -5.5 -4.5 -3.5 -2.5
70 83 100 130 140 180 220 290 400
第三章 光学仪器
目视光学仪器：和人眼配合使用的仪器
应用光学讲稿
本章主要解决的问题：
• 眼睛的构造 • 望远镜、显微镜的工作原理 • 眼睛与目视光学仪器配合的问题、眼睛缺陷 及调整 • 如何选择成像光束的位置 • 选择成像光束的原则 • 限制光束的方法
应用光学讲稿
§3-1 人眼的光学特性
• 人眼的构造
应用光学讲稿
和显微镜一样，对着物方的透 镜称为物镜，对着人眼的透镜 称为目镜。
物镜的像方焦点和目镜的物 方焦点重合。 组合系统的Δ=0，有时，将Δ=0 定义为望远镜，将Δ不等于0定 义为显微镜。
应用光学讲稿
望远镜的视放大率
y’ -ω f’物 视放大率公式
tg仪 tg眼
F’物 F目
ω’
－f目
应用光学讲稿
50 倍 天 文 望 远 镜 拍 摄 的 月 球 照
应用光学讲稿
Hubble Space Telescope, 重 11.5 吨, 主透镜半径2.4 米。
应用光学讲稿
早期的宇宙 The deepest space so far, taken by HST (Hubble Space Telescope)
盲点实验
应用光学讲稿
视觉的产生
外界的光线进入人眼 成像在视网膜上，产生视神经脉冲 通过视神经传向大脑，经过高级的中枢神经 活动，形成视觉 物理过程，生理过程，心理过程
应用光学讲稿
人眼的光学特性
视轴：黄斑中心与眼睛光学系统的像方节点连线 人眼视场：观察范围可达150º 头不动，能看清视轴中心6º －8º
应用光学讲稿
• 显微镜的工作原理
显微镜就是一个复杂化的放大镜 y tg仪 放大镜的视角 f'
提高放大镜的视放大率的途径： 减小焦距，刚才分析，可能性不大。 增大物高。 可以设想先将物体通过一个透镜放大成像， 然后再通过放大镜放大，由人眼观察。 这就是显微镜的原理
应用光学讲稿
应用光学讲稿
放大100倍后的鱼胚胎照片 显微镜下的硅藻
被观察物体首先要成像在视网膜上，而且对 人眼的张角大于人眼的视角分辨率时，才能被看清。
对各类目视光学仪器的共同要求
1、成像在无限远 正常人眼在自然状态下，无限远物体成像在视网膜上
应用光学讲稿
2、增大视角
直接观察： 用仪器观察：
-y’眼=π ’ tg ω眼
-y’仪=π ’ tg ω仪
应用光学讲稿
用仪器观察视网膜上的像高和人眼直接观察视网膜上 的像高之比表示了仪器的放大作用，称为视放大率， 用Г 表示。 Г＝
应用光学讲稿
望远镜的类型
开卜勒望远镜：物镜和目镜的焦距均为正 Г<0，成倒像 通常须加倒像系统 体积较长
系统中存在实像， 可安装分划板，进 行测量和瞄准 军用光学仪器
应用光学讲稿
望远镜的类型
伽里略望远镜：物镜焦距为正，目镜焦距为负 Г>0，成正像 不须加倒像系统 体积较短。
系统中不存在实像， 不能安装分划板，无 法进行测量和瞄准 常用于观察。
角膜，前室和水晶体 相当于镜头部分。
应用光学讲稿
视网膜：视神经细胞和神经纤维，相当于感光底片 黄斑：视网膜上视觉最灵敏的地方 这两项相当于感光部分 虹膜：水晶体前面 的薄膜，中心有一 圆孔，成为瞳孔， 随着入射光能量的 多少，瞳孔直径可 放大或缩小。 相当于可变光阑
应用光学讲稿
盲点：视神经纤维的 出口，没有感光细胞， 不产生视觉
F’
• 近视眼看不清无限远目标，看到的最远距离（远 点）是有限的，这个距离是近视眼视网膜的物方 共轭面；眼睛依靠调节只能看清远点以内的物体
应用光学讲稿
• 近视程度用远点距离对应的视度表示
比如远点距离在眼睛前方0.5m，对应的视度
SD=1/(-0.5)= -2 医学上眼镜度数与视度相对应，数量上的关系为 1 视度＝100゜
应用光学讲稿
显微镜下的雪花
应用光学讲稿
• 显微镜的工作原理
目镜
物镜
y’ -y
f’物
F’物
Δ
F目
-f目
ω仪
显微镜由两组透镜组成，对着物体的透 镜称为物镜，对着人眼的透镜称为目镜。
应用光学讲稿
目镜
物镜
y’ -y
f’物
F’物
Δ
F目
-f目
ω仪
tg ω眼 =
y 250
tg ω仪 =
y’ f’目
=
-Δ
f’物 f’目
F’
应用光学讲稿
正常人眼观察近距离物体时，依靠人眼视度调节 可以将F’点前移，使像成在网膜上 人眼能看清的最远距离称为远点，远点是人眼自 然状态下与网膜像相共轭的物平面位置
人眼依靠调节能看清的最近距离称为近点
应用光学讲稿
2、近视眼的特点 • 近视眼的像方焦点在视网膜前方，无限远物不能 成像在网膜上
应用光学讲稿
5、远视眼的校正
F’
远点
采用正透镜，焦距等于远点距离
应用光学讲稿 PRK－ 准分子激光角膜切削
术
=193nm far
ultraviolet laser LASIK－准分子激光 原位角膜磨镶术
' min
应用光学讲稿
对线的分辨率：分辨率可以提高到10’’
在很多仪器中需要瞄准， 瞄准的方式有
对线的分辨率称为对准 精度，右图的对准精度 都是10”