近似数精确度的两种形式

近似数精确度的两种形式任何一个近似数，都可以用精确度来表示它与准确数的接近程度。

一般地，一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位。

这时，从左边第一个不是0的数字起，到末位数字止，所有数字都是这个数的有效数字。

不难发现，描述一个近似数的精确度有两种形式：一是精确到哪一位；二是保留几个有效数字。

那么，怎样确定一个近似数的精确度？一、近似数是小数或整数例1 下列由四舍五入得到的近似数，各精确到哪一位，各有哪几个有效数字？（1）10.45 （2）78 （3）0.01020分析：这些近似数是小数或整数，其精确度的确定，应从精确到哪一位和有效数字的基本概念入手。

在确定有效数字时，0不能多算也不能少算。

以从左至右第一个不是0的数字为界，左边的0不算，右边的0都要算。

解：（1）10.45，精确到百分位或精确到0.01，有4个有效数字：1，0，4，5。

（2）78，精确到个位或1，有两个有效数字：7，8。

（3）0.01020，精确到十万分位或精确到0.00001，有4个有效数字：1，0，2，0。

二、带有计数单位的近似数例2 下列由四舍五入得到的近似数，各精确到哪一位，各有哪几个有效数字？（1）5.8万（2）10亿（3）87.01千分析：这些近似数都带有计数单位，其有效数字的确定与计数单位无关。

在确定精确到哪一位时，若计数单位前面是整数，它就精确到计数单位；若计数单位前面是小数，则先将近似数还原成用1作计数单位的数，再根据近似数的位数，从最高位数起，数到哪个数位，就精确到哪一位。

解：（1）5.8万（即58000），精确到千位，有两个有效数字：5，8。

（2）10亿，精确到亿位，有两个有效数字：1，0。

（3）87.01千（即87010），精确到十位，有4个有效数字：8，7，0，1。

三、用科学记数法表示的近似数例3 下列由四舍五入得到的近似数，各精确到哪一位？各有哪几个有效数字？分析：用科学记数法表示的近似数，确定它们的有效数字时，只看不是10的幂的数的有效数字，确定该数精确到哪一位时，可把10的幂看成计数单位或把近似数还原成不用科学记数法表示的数，再根据近似数的位数，从最高位数起，数到哪个数位就精确到哪一位。

解读近似数的精确度近似数的精确度表示近似数与准确数的接近程度。

精确度有两种表示形式：一是用精确到哪一位（精确位）表示，一是用保留几个有效数字（有效数字）表示。

精确度的两种表示形式的实际意义及取值要求是不一样的，在学习时要加以区别。

一、解读“精确到哪一位”⑴对一个数取近似数，要求精确到某一个数位，我们就将所要求精确到的数位后一位数字“四舍五入”得到近似数。

该近似数最后一位数是由“四舍五入”得到的数，最后一位数所在的数位即是精确到的数位。

如：近似数3.52，最后一位数字2是由“四舍五入”得到的数，2所在的数位为百分位，即近似数3.52精确到百分位。

又如：9989.653（精确到个位）的近似数，将个位后的十分位上的6“四舍五入”，近似数为9990。

1.35835（精确到0.001）的近似数，将千分位后的万分位上的3“四舍五入”，近似数为1.358。

⑵精确到哪一位表示的实际意义：主要用于表示近似数与准确数之间误差绝对值的大小。

例如，在测量长度时，精确到0.1米，说明结果与实际相差不大于0.05米。

⑶确定用科学记数法表示的近似数、带数量级单位的近似数精确到哪一位时，要先将该数还原成原来的数，再看它最后一个数字所在的数位即精确到哪一位。

如近似数 1.230×106，还原成原数为1230000，最后一位数字0所在的数位为千位，因此近似数1.230×106精确到千位（而不是千分位！）。

近似数5.04万，还原成原数为50400，最后一个数字4所在的数位为百位，因此近似数5.04万精确到百位（而不是百分位！）。

⑷近似数的最后一位数字是由“四舍五入”得到的数，根据近似数可以确定准确数的取值范围。

一般地，近似数m所表示的准确数a 的范围是：m－精确位后一位的5个单位≤a＜m+精确位后一位的5个单位。

如近似数8.40所表示的准确数a的范围是8.40－0.005≤a＜8.40+0.005，即8.395≤a＜8.405。

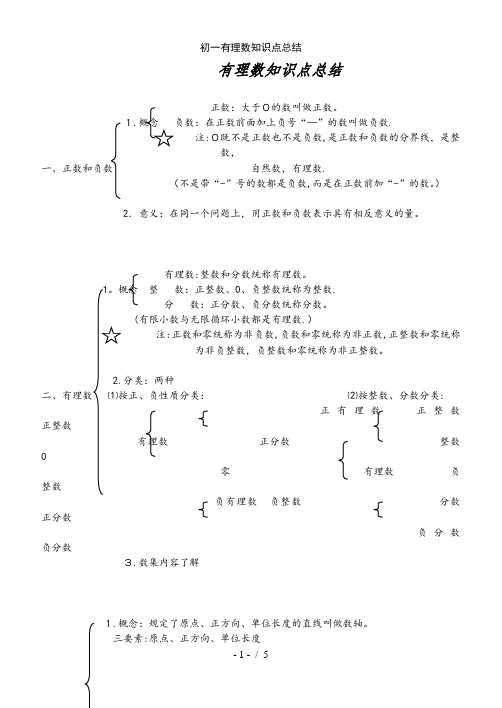
有理数知识点总结正数：大于０的数叫做正数。

１..注:０既不是正数也不是负数,是正数和负数的分界线，是整数，一、正数和负数自然数，有理数.（不是带“-”号的数都是负数,而是在正数前加“-”的数。

）2．意义：在同一个问题上，用正数和负数表示具有相反意义的量。

有理数:整数和分数统称有理数。

概念整数：正整数、0、负整数统称为整数.分数：正分数、负分数统称分数。

(有限小数与无限循环小数都是有理数.）注:正数和零统称为非负数,负数和零统称为非正数,正整数和零统称为非负整数，负整数和零统称为非正整数。

分类：两种⑵按整数、分数分类:正有理数正整数正整数有理数正分数整数0零有理数负整数负有理数负整数分数正分数负分数负分数３.数集内容了解１.概念：规定了原点、正方向、单位长度的直线叫做数轴。

三要素:原点、正方向、单位长度2。

对应关系：数轴上的点和有理数是一一对应的。

三、数轴比较大小：在数轴上，右边的数总比左边的数大 .3。

应用求两点之间的距离:两点在原点的同侧作减法，在原点的两侧作加法.(注意不带“+”“—”号）代数:只有符号不同的两个数叫做相反数.１.概念（0的相反数是0）几何：在数轴上,离原点的距离相等的两个点所表示的数叫做相反数。

2.性质：若a与b互为相反数，则a+ｂ=0,即ａ=-b；反之，若a＋b=０,则a与ｂ互为相反数。

四、相反数两个符号：符号相同是正数，符号不同是负数。

3.多重符号的化简多个符号:三个或三个以上的符号的化简，看负号的个数，当“—”号的个数是偶数个时，结果取正号当“—”号的个数是奇数个时，结果取负号1．概念:乘积为1的两个数互为倒数。

（倒数是它本身的数是±1；０没有倒数)五、倒数2。

性质若a与ｂ互为倒数，则a·b=1;反之,若a·b=1，则a与b互为倒数。

若a与b互为负倒数，则ａ·b=-１；反之，若a·b＝－1则a与b互为负倒数。

1.几何意义:一般地，数轴上表示数ａ的点与原点的距离叫做数a的绝对值.一个正数的绝对值是它的本身（若｜a｜=｜ｂ｜，则a＝b或a＝﹣b）2。

2.7 近似数◆目标指引1．通过实例经历近似数和准确数概念的产生过程．2．感受近似数的精确度的两种表示方式．3．能说出由四舍五入得到的有理数的精确位数和有效数字．4．会根据预定精确度取近似值．◆要点讲解1．近似数：与实际接近的数．2．准确数：与实际完全符合的数．3．有效数字：一个近似数，从左边第一个不是0的数字起，到末位数字止（到精确的数为止），所有的数字都叫做这个数的有效数字．4．一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位．5．精确度：一个数的近似程度即精确到哪一位．◆学法指导1．精确度的形式有两种：精确到哪一位；保留几个有效数字．2．有效数字的个数从近似数左边第一个不为0的数字起，到精确到的数位止，这中间的所有数字，包括0，重复的数字，都不能漏掉．3．近似数的小数点后的末尾数字0是不能去掉的．4．给定一个近似数，要确定其精确度，题目中要给出一定要求，•主要由该近似数的最后一位有效数字在该数中所处的位置决定．5．对较大的数（如188600）取近似数时，结果一定要用科学记数法表示．◆例题分析【例1】下列由四舍五入得到的近似数各精确到哪一位，各有哪几个有效数字？（1）31.7；（2）0.002314；（3）5.39万．【分析】（1）最末位数字7是十分位上的数字；（2）最末位上的4•是百万分位上的数；（3）5.39万=53900，其中9是百位上的数字．【解】（1）31.7精确到十分位（即精确到0.1），有3个有效数字：3，1，7．（2）0.002314精确到百万分位（即精确到0.000001），有4个有效数字：2，3，1，4．（3）5.39万精确到百位，有3个有效数字：5，3，9．【注意】看一个数精确到哪一位，是看这个数的最末位数字在什么位置，就精确到了哪一位．根据有效数字的定义，第一个非零数字前面的零不能作为有效数字，而后面的零则是它的有效数字，对用“万”为单位的数5.39万，看它精确到哪一位．则先要将它写成53900，再看属于哪个数位上的数，就精确到哪一位，•而看5.39万的有效数字的个数，就不需要写成53900的形式，直接看5.39万中单位“万”前面的有效数字的个数．【例2】用四舍五入法按括号里的要求对下列各数取近似值：（1）0.6779（精确到百分位）；（2）29.756（保留一位小数）；（3）80610（精确到百位）；（4）3.1449（保留三个有效数字）；（5）2.04×105（精确到万位）．【分析】四舍五入法取近似值，根据题目要求精确到哪一位，把这一位的下一位进行四舍五入．【解】（1）0.6779≈0.68；（2）29.756≈29.8；（3）80610≈8.06×104；（4）3.1449≈3.14；（5）2.04×105≈2.0×105．【注意】（1）取近似数时末尾的0不能去掉，例如2.0×105不能写成2×105，它们的精确度不同；（2）大于10的数取近似数时，先将此数用科学记数法表示出来，再取近似值．例如第（3）题结果不能写成80600，它有五个有效数字，精确到个位，结果应写成8.06×104或806百；（3）取近似数时，不能用“=”，而应用“≈”．◆练习提升一、基础训练1．下列各数哪个为准确数（）A．初一年级共有400人B．小明的体重为63千克C．北京市人口有1382万人D．月球离地球的距离是38万千米2．由四舍五入法得到的近似数0.3080，它的精确度是精确到（）A．百分位B．千分位C．万分位D．十万分位3．由四舍五入法得到的近似数0.0307的有效数字的个数是（）A．3个B．4个C．5个D．6个4．保留三个有效数字得到31.0的是（）A．31.22 B．31.05 C．30.95 D．30.9355．38490按四舍五入法取近似数，保留两个有效数字，用科学记数法表示是（）A．3.8×104B．3.8×103C．3.7×103D．3.85×1046．下列说法正确的是（）A．近似数1.8与1.．80表示的意义一样B．4.5万精确到万位C．圆周率等于3.14 D．1.00有三个有效数字7．由四舍五入得到的近似数0.851，它所表示的准确数a的范围是（）A．0.8050≤a<0.8515 B．0.8505≤a<0.8515C．0.8514≤a<0.852 D．0.8500≤a<0.85158．57645精确到千位是_______．9．今年3月，国家统计局公布我国总人口数为139533万人，•如果以亿为单位保留两位小数，可以写成_________亿人．二、提高训练10．我国的国土面积约为9.60×106平方千米，由四舍五入得到的近似数9.6×106（）A．有两个有效数字，精确到百分位B．有两个有效数字，精确到千位C．有两个有效数字，精确到万位D．有两个有效数字，精确到十万位11．按实际情况取近似值：（1）全班51人参加100米跑测验，每6人一组，问至少分成几组？（2）一辆汽车要装4个轮胎，51个轮胎能装配成几辆汽车？12．张华在体检时，量得身高为1.70米，他在登记时写的是1.7米，•测量结果与登记数是否一致？为什么？三、拓展训练13．如图，直角梯形上、下底分别是3.54厘米和5.32厘米，求阴影部分的面积．（ 取3.14，精确到0.01厘米2）14．甲，乙两个同学身高都约是1.6×102厘米，但甲说他比乙高9厘米，请问有这种可能吗？若有可能，请举例说明．参考答案1．A 2．C 3．A 4．C 5．A 6．D 7．B 8．5.8×1049．13.95 10．D 11．（1）9组（2）12辆12．不一致，理由略13．5.85厘米214．有可能，举例略。

第三章 生活中的数据一、知识网络：1.科学计数法科学计数法表示一个数就是把一个数写成a ×10n 的形式，其中1≤|a|<10,n 为正整数且n 的值等于这个数的整数部分的位数减去1.（1）当它表示一个绝对值大于10的数时，n 为正整数且n 的值等于这个数的整数部分的位数减去1.（2）当它表示一个绝对值小于101的数时，n 为负数且n 的绝对值等于这个数的第一个非零数前面的零的个数（包括小数点后面的零）.2.近似数和有效数字（1）有效数字：对于一个近似数，从左边第一个不为0的数字起，到精确到的数位为止，所有的数字都是这个数的有效数字.（2）精确度：一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位.近似数的精确度有两种形式：①精确到某一位；②保留几个有效数字.（3）用科学计数法表示近似数：一个绝对值比较大的的整数取近似值时，如果整数位数多于保留的有效数字的个数，或表示整十、整百……的近似数，一般用科学计数法表示.注意：在说明一个数的精确度时，主要看最后一个有效数字的位数，在哪一位精确度就说成精确到哪一位，对于科学计数法表示的数应注意将其还原为原来的数后，再确定它的精确度.3.数学中常见的信息统计图常见的统计图有条形统计图、折线统计图、扇形统计图，除此之外，媒体中还常见一些形象统计图. （1）如何利用统计图中的信息对统计图的利用，首先应明白统计图所反映的是关于哪个量的信息，并且其基本数量单位是什么，还要懂得统计图是用何种方式来显示数量的大小.从统计图中读出的信息，为以后发展提供参考，或者得出一定的归纳性的结论.在这里度量单位应加以重视.(2)如何制作形象的统计图制作统计图的关键是选择什么样的直观形象来反映所统计的数量，并且要在直观图上注明数字，数字单位也要在图中注明.至于数量的多少可以用大小、高低或多少来表示.（3）如何有效估计估计的关键是确定一个参照物，再确定度量，经过大致的测量，运用简单的数学运算来进行估计，可以尝试用不同的方法、不同的角度、或选择不同的参照物去进行估计、验证.三、应注意的问题1．用10的负整数指数幂表示一个较小的数时，若小数点后连续零的个数为n，则10的指数为－（n+1）.2．用科学计数法表示一个近似数时，10的整数次幂前的系数是只带一位整数的小数，它有几位数这个近似数就有几个有效数字.3．应当学会根据不同的问题，进一步体会不同统计图的特点，选择适当的方法把杂乱无章的数据整理得简洁、醒目和富有个性.5．注意收集数据、处理数据等过程的真实性和科学性.6.常见的思维误区（1）在科学计数法表示绝对值较大或较小的数时，常会出现以下错误认识：①n的正负写错了；②a的值不是1～10之间.（2）近似数与有效数字的常见误区有：①较大数中的精确度确定有错误；②较大数中的近似数取的不对，前者易与较小数的情形混淆，后者常出现以较小数替代原数.（3）对于辨图、作图、分析图表问题，常出现以下错误：①不会分析、识图，不知从何入手；②不仔细分析，盲目得出结论；③制作图表粗糙、不精确.四、考点精析考点1：感受小数------认识百万分子一例1 （2006年江西省）某运动场的面积为300 m2，则它的万分之一的面积大约相当于（）A. 课本封面的面积B. 课桌桌面的面积C. 黑板表面的面积D. 教室地面的面积析解：某运动场的面积为300m2，即3000000cm2，它的万分之一为300cm2，相当于一本课本封面的面积，故选A.练习1：（1）（辽宁锦州市）锦州市宝石广场占地面积约为12555米2，它的面积与一个班级教室面积的倍数关系，下列最接近的是()A.40倍B.80倍C.100倍D.150倍（2）（2006年江苏淮安市）巳知某种型号的纸100张厚度约为lcm，那么这种型号的纸13亿张厚度约为（）A．1.3×107km B．1.3×103km C．1.3×102km D．1.3×10km答案提示：（1）D；（t考点2：表示小（大）数------科学计数法例2 （1）（2006年浙江诸暨市）国家质检总局出台了国内销售的纤维制品甲醛含量标准, 从2003年1月 1 日起正式实施.该标准规定:针织内衣. 床上用品等直接接触皮肤的制品,甲醛含量应在百万分之七十五以下. 百万分之七十五用科学记数法表示应写成( )A．75×10-7；B．75×10-6；C．7.5×10-6；D．7.5×10-5（2）（2006年山西临汾市）2006年5月20 日，世界上规模最大的混凝土重力坝三峡大坝浇筑完成．建成后，三峡水库库容总量为39 300 000 000立方米．用科学计数法表示库容总量为________立方米．析解：（1）100000075=0.000075=7.5×10－5.故选D.（2）39 300 000 000=103.9310⨯.练习2：(1)(2006年四川眉山市)已知空气的密度为0.001239克/厘米3，用科学计数法表示是________克/厘米3.(2)（2006年北京市海淀区）据媒体报道，我国因环境污染造成的巨大损失，每年高达680000000元，这个数用科学计数法表示正确的是（ ）A.6.8×109元B.6.8×108元C.6.8×107元D.6.8×106元答案提示：（1）1.239×10－3；2. B. 考点3：近似数例3 （2006年广东深圳市）今年1---5月，深圳市累计完成地方一般预算收入216.5 8亿元，数据216.58亿是精确到（ ）A.百亿位B.亿位C.百万位D.百分位析解：将数据还原则是21658000000，而8在百万位，所以216.58亿是精确到百万位，故选C. 练习3：下列问题中，哪些数据是准确数，哪些是近似数？近似数各精确到哪一位？ （1）某校七年级4班有40名同学，平均身高约为1.56米，平均体重约为50.6千克. （2）某商场5月份的营业额约为30万元，该商场经理的年收入约为1.5万元.析解：（1）学生人数40是精确数，平均身高和平均体重是近似数，其中1.56精确到百分位，50.6精确到十分位.（2）该题中的5月份的营业额和经理的年收入都是近似数，其中40精确到个位，1.5精确到十分位. 考点4：有效数字例4 （2006年辽宁锦州市）2005年10月17日新华网报道：“5天前从酒泉卫星发射中心启航的神舟六号飞船，在平安飞行115小时32分后重返神州.”用科学记数法表示神舟六号飞船飞行的时间是____秒(保留三个有效数字).析解：由于本题中的时间单位有时、分、秒，不统一，故应先把单位统一化为秒.115小时32分=115×3600+32×60=415920（秒）=4.1592×105（秒），保留三个有效数字为4.16×105秒. 练习4：（1）鲁迅先生十分重视精神文化方面的消费，据史料记载，他在晚年用于购书的费用约占收入的15.6％,则近似数15.6％有_______个有效数字.（2）（2006年湖北咸宁市）随意丢弃塑料袋，会对环境产生不良的影响．某班环保小组经抽样调查得知平均每个家庭一周内丢弃15个塑料袋．我市约有75万个家庭，全市每周丢弃的塑料袋的个数用科学记数法表示大约为 个（结果保留两个有效数字）．答案提示：（1）3；（2）71.110⨯. 考点5：数据的描述------统计图例5 （2006年北京市）根据北京市统计局公布的2000年、2005年北京市常住人口相关数据，绘制统计图表如下：人数(万人 ) 2000年、2005年北京市常住人口数统计图％79.00~14岁 14~65岁65岁以上2005年北京市常住人口各年龄段人数统计图2000年、2005年北京市常住人口中受教育程度情况统计表（人数单位：万人）请利用上述统计图表提供的信息回答下列问题：（1）从2000年到2005年北京市常住人口增加了多少万人？（2）2005年北京市常住人口中，少儿(0～14岁)人口约为多少万人？（3）请结合2000年和2005年北京市常住人口受教育程度的状况，谈谈你的看法。

确定近似数精确度的有效方法湖北省孝感市孝南区车站中学（432011）殷菊桥纵观历年的中考题，近似数的精确度的考查出现的频率相当高，而考生在这方面的失误也不低，应引起关注。

课本上说，在实际计算时，往往对运算结果的精确度提出要求，这个要求可以是精确到哪一位，也可以是保留几个有效数字。

那么如何从这两个方面有效确定近似数的精确度呢？一确定近似数精确到哪一位一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位。

⒈用常规方法确定精确到哪一位当近似数是一般数的形式时，它最后一位在什么位上，就说这个近似数精确到哪一位。

例近似数2004最后一位在个位上，就说2004精确到个位；2004.00最后一位在百分位上，就说它精确到百分位或精确到0.01（因为最后一个0所在数位的计数单位是0.01）。

⒉用还原法确定精确到哪一位当近似数是科学记数法形式或带有计数单位形式时，先把它还原成一般数，再看原数的最后一位在哪一位上就说这个近似数精确到了哪一位。

例如近似数8.67×105＝867000，还原后7在千位上，所以它精确到千位；近似数8.03万＝80300，还原后3在百位上，所以它精确到百位。

对于8.67×105和8.03万这两个数，不能因为8.67和8.03中的7和3在百分位上而说它们精确到百分位。

对于带有计数单位的数8.03万也可不还原，因为8、0、3所在数位依次是万位、千位、百位，故8.03万精确到百位。

⒊根据精确到哪一位取近似值用四舍五入法按精确到哪一位取近似值时，先找到相应的数位，再将其后紧跟的一位数字四舍五入取近似值。

例如，把0.12345精确到0.001只考虑万分位上的数，得0.123。

当把一个数精确到整数位时，可以先四舍五入，再用科学记数法表示成a×10n（1≤a＜10，且n为整数），例如30350（精确到百位）≈30400＝3.0400×104，然后将百位4后面的0去掉，得30350≈3.04×104。

确定近似数精确度的有效方法湖北省孝感市孝南区车站中学（432011）殷菊桥纵观历年的中考题，近似数的精确度的考查出现的频率相当高，而考生在这方面的失误也不低，应引起关注。

课本上说，在实际计算时，往往对运算结果的精确度提出要求，这个要求可以是精确到哪一位，也可以是保留几个有效数字。

那么如何从这两个方面有效确定近似数的精确度呢？一确定近似数精确到哪一位一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位。

⒈用常规方法确定精确到哪一位当近似数是一般数的形式时，它最后一位在什么位上，就说这个近似数精确到哪一位。

例近似数2004最后一位在个位上，就说2004精确到个位；2004.00最后一位在百分位上，就说它精确到百分位或精确到0.01（因为最后一个0所在数位的计数单位是0.01）。

⒉用还原法确定精确到哪一位当近似数是科学记数法形式或带有计数单位形式时，先把它还原成一般数，再看原数的最后一位在哪一位上就说这个近似数精确到了哪一位。

例如近似数8.67×105＝867000，还原后7在千位上，所以它精确到千位；近似数8.03万＝80300，还原后3在百位上，所以它精确到百位。

对于8.67×105和8.03万这两个数，不能因为8.67和8.03中的7和3在百分位上而说它们精确到百分位。

对于带有计数单位的数8.03万也可不还原，因为8、0、3所在数位依次是万位、千位、百位，故8.03万精确到百位。

⒊根据精确到哪一位取近似值用四舍五入法按精确到哪一位取近似值时，先找到相应的数位，再将其后紧跟的一位数字四舍五入取近似值。

例如，把0.12345精确到0.001只考虑万分位上的数，得0.123。

当把一个数精确到整数位时，可以先四舍五入，再用科学记数法表示成a×10n（1≤a＜10，且n为整数），例如30350（精确到百位）≈30400＝3.0400×104，然后将百位4后面的0去掉，得30350≈3.04×104。