下载文档原格式
热力学第一定律解析式
热力学第一定律是能量守恒的基本原理，它描述了能量在系统中的转移和转化过程。
热力学第一定律的解析式可以表示为：
ΔU = Q - W
其中，ΔU表示系统内能的变化，Q表示系统所吸收或释放的热量，W表示系统对外做功。
这个方程表明，系统内能的变化ΔU等于吸热Q与做功W 之差。
正负号的选择遵循以下约定：
•当系统吸收热量或对外做功时，相应的量取正值；
•当系统释放热量或外界对系统做功时，相应的量取负值。
该方程说明了能量在系统内部的转化和转移，可以应用于各种热力学过程的分析。
例如，在等容过程中（体积不变的过程），做功为零，方程简化为：
ΔU = Q
这表示系统的内能变化仅由吸热量决定。
在等压过程中（压强不变的过程），方程可以写作：
ΔU = Q - PΔV
其中，P表示系统的压强，ΔV表示体积的变化。
这个方程说明了在等压过程中，内能变化除了吸热量外，还受到体积变化对做功的贡献。
需要注意的是，以上方程都是在封闭系统中成立的，即系统与外界没有物质交流。
如果考虑了物质的进出，应使用开放系统或闭合系统的相应扩展形式。
此外，方程中的能量和热量单位可以是焦耳（J）或卡路里（cal），功的单位可以是焦耳或千焦耳（kJ）。
对于不同的问题，需要根据具体情况和所使用的单位来适当调整。
第一章1、平衡状态定义：在不受外界影响的条件下，工质（或系统）的状态参数不随时间变化而变化的状态。
平衡与均匀：均匀一定平衡、平衡不一定均匀平衡与稳定：稳定不一定平衡，平衡一定稳定特点：平衡状态具有确定的状态参数。
工程热力学只研究系统平衡状态的原因：平衡状态概念的提出，使整个系统可用一组统一的、并具有确定数值的状态参数来描述其状态，使热力分析大为简化。
2、状态参数状态参数是定量描述工质状态的状态量。
其性质是状态参数的变化量只取决于给定的初、终状态，与变化过程的路径无关。
如果系统经历一系列状态变化又返回初态，其所有状态参数的变化量为零。
六个基本状态参数：P V T内能焓熵3、准平衡过程定义：由一系列连续的准平衡态组成的过程称为准平衡过程，又称准静态过程。
实现条件：（1）推动过程进行的势差（压差、温差）无限小；（2）驰豫时间短，即系统从不平衡到平衡的驰豫时间远小于过程进行所用的时间。
特点：系统内外势差足够小，过程进行得足够慢，而热力系恢复平衡的速度很快，所以工程上的大多数过程都可以作为准平衡过程进行分析。
建立准平衡过程概念的好处：（1）可以用确定的状态参数描述过程；（2）可以在参数坐标图上用一条连续曲线表示过程。
4、可逆过程准平衡过程概念的提出只是为了描述系统的热力过程，但为了计算系统与外界交换的功量和热量，就必须引出可逆过程的概念。
定义：过程能沿原路径逆向进行，并且系统与外界同时返回原态而不留下任何变化。
实现条件：在满足准平衡过程条件下，还要求过程中无任何耗散效应（通过摩擦、电阻、磁阻等使功变为热的效应）建立可逆过程概念的好处：（1）由于可逆过程系统内外的势差无限小，可以认为系统内部的压力、温度与外界近似相等，因此可以用系统内的参数代替复杂、未知的外界参数，从而简化问题，使实际过程的计算成为可能，即先把实际过程当作可逆过程进行分析计算，然后再用由实验得出的经验系数加以修正；（2）由于可逆过程是没有任何能量损失的理想过程，因此，它给出了热力设备和装置能量转换的理想极限，为实际过程的改善指明了方向。
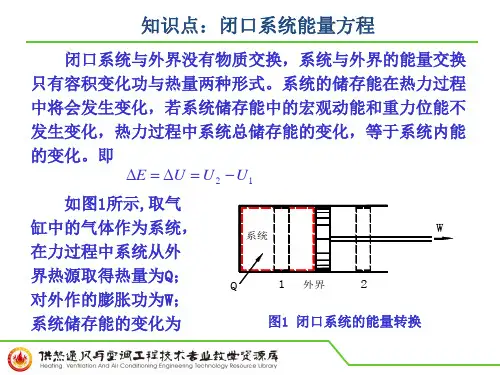
能源转换利用的关系风水化核地太生物质能能学能能热能阳能光电燃料电光热聚变裂变燃烧水水轮风转换供暖热能转换池车机车机械能热机90%电动机发电机电能如何用所学知识去解释RefrigeratorIcebox电冰箱热力学第定律热力学第一定律The First Law of Thermodynamics 第四讲：热力学能和闭口系能量方程热力学第一定律热力学第定律学习目的深刻认识热力学第定律的实质能量守恒；认深刻认识热力学第一定律的实质——识功和热——通过热力系统边界的能量交换（定义、特性、计算）；掌握闭口系能量方程基本表达式。
基本要求¾掌握第一定律的实质；功和热的异同¾掌握热力学第一定律应用热力学第一定律的本质本转换守恒律在过中的应本质：能量转换及守恒定律在热过程中的应用•18世纪初，工业革命，热效率只有1%•1842年，J.R. Mayer 阐述热一律，但没有y 引起重视•1840-1849年，Joule 用多种实验的一致性证明热一律，于•1909年，C. Caratheodory 最后完善热一律证明热律，于1850年发表并得到公认年y 最后完善热律Conservation of energy Conservation of energy“D i i i“During an interaction , energy can change from one form to can change from one form to another but the total amount of energy remains constant”Energy cannot be created or destroyed One of the most fundamental laws of nature焦耳实验1、重物下降，输重物下降输入功，绝热容器内气体T↑2、绝热去掉，气、绝热去掉气体T↓，放出热给水，T恢复原温原温。
焦耳实验水温升高可测得热量，物降得功Mechanical重物下降可测得功equivalent of heat 热功当量1cal =41868kJ 1 cal = 4.1868 kJ工质经历循环:δQ =δWQ闭口系循环的热律表达式闭口系循环的热一律表达式δQ =δW要想得到功必须化费热能或其它能量要想得到功，必须化费热能或其它能量热律又可表述为第类永动机是热一律又可表述为“第一类永动机不可能制成的”不可能制成的pPerpetual –motion machine of the first kind第一类永动机第类永动机Q汽轮机电锅炉W net加发电机凝热器汽器给水泵Q out第一类永动机第类永动机“饮水鸟”内的液体是乙醚一类易挥发的液体，在饮水鸟内的液体是乙醚类易挥发的液体，在高温里很容易蒸发，而液体的饱和蒸汽所产生的压力又会随温度的改变而剧烈的改变。
a a.头部受冷，气压下降，尾部的液体因为吸力沿颈部上升。
这样头的重量在增加，尾部的重量在减轻，重心位置发生变化，当重心超过脚架支点而移向头部时，鸟就俯下身到平衡位置。
这个位置可以通过鸟嘴的重量来调试。
b.头部降低，内部发生两个变化。
一是“饮水鸟”的嘴浸到了水，这样鸟头被打湿。
二是上下的蒸汽区域连通，两部分气体混合，没有了气压差，但由于吸收了周围空气的热量，蒸汽的温度略有上升。
这时上升到头部的液体，在本身的重量作用下流向下端尾部。
c.尾部变重，头部向上翘，液体全部集中到尾部，同时，头部的蒸汽因为刚粘到的水又开始冷却。
热一律的推论⎯热力学能Internal energyI l热力学能的导出闭口系循环δQ =δW(δQ -δW ) = 0热力学能的导出δQ -δW ) = 0对于循环1a2c1 (Q)1221()()0a cQ W Q Wδδδδ−+−=∫∫p1b对于循环1b2c1Qac1221()()0b cQ W Wδδδδ−+−=∫∫2()()Q W Q Wδδδδ∴−=−V1212a b∫∫状态参数热力学能及闭口系热一律表达式热力学能及闭口系热律表达式d U Q 定义U = δQ -δW 热力学能U 状态函数δQ =d U +Q d U + δWQ = ΔU + W闭口系热一律表达式！！！两种特例绝功系δQ = d UW =绝热系δW= -d UU热力学能U 的物理意义d U = δQ -δWδWδQd U U 代表某微元过程中系统通过边界交换的微热量与微功量两者之差值，也即系统内部能量的变化。
U 代表储存于系统内部的能量⎯热力学能（内能）热力学能的微观组成microscopic forms of internal energy 移动translation 分子动能分能√转动rotation 振动vibration 分子位能binding forces 热力√化学能chemical energy学能nuclear energy 核能gytotal energy 系统总能total energymacroscopic forms of energy 外部储存能macroscopic forms of energy 宏观动能kinetic E = mc 2/2k 宏观位能potential E p = mgz 机械能系统总能E = U + E k + E p =++e = u + e k + e p 一般与系统同坐标常用d d 般与系统同坐标，常用U , d U , u , d u宏观动能与内动能的区别18热力学能的说明state property•热力学能是状态量state property•U : 广延参数[ kJ ]U广延参数[kJ]•u : 比参数[kJ/kg]g•热力学能总以变化量出现，热力学能零点人为定J热力学能单位kJUΔ工程中关心热一律的文字表达式热律的文字表达式热律热一律: 能量守恒与转换定律=进入系统离开系统系统内部储存-的能量的能量能量的变化TotalTotal Change in Total energyTotal energy in the total =enteringthe system leaving the energy of the system -the systemsystem the system闭口系能量方程E b l f l d t Point function---Exact differentials---d 一般式Energy balance for closed system Path function---Inexact differentials---δδW δQ般式δ= d U + δW Q Q = ΔU + W=d +δq d u δw q = Δu + w单位工质2)适用条件：1）任何工质2)任何过程闭口系能量方程中的功Generalized Workδq = d u + δw功（δw ）是广义功Generalized Work ⎯闭口系与外界交换的功量准静态容积变化功p d v拉伸功δw 拉伸= -τd l =表面张力功δw 表面张力= -δd A=l +δw = p d v -τd l -δd A +…...门窗紧闭房间用电冰箱降温以房间为系统绝热闭口系闭口系能量方程U W=Δ+Refrigerator Q=gIceboxQ−W<电U WΔ=>冰T箱门窗紧闭房间用空调降温以房间为系统闭口系闭口系能量方程U W=Δ+Air-Q <空conditioner0Q =−0W <调QU Q WΔTQ W>开口系能量方程E b l f ti Energy balance for open system δm in u 能量守恒原则in1δW net 进入系统的能量-22in c δm out tgz in离开系统的能量δQu out =系统储存能量的变化1gz out22out c开口系能量方程的推导δm inu in21inc δW net gz in 2δm outu out 这个结果与实验不符gz out少了推进功21c δQδQ + δm in (u + c 2/2 + gz )in +/2+d 2out -δm out (u +c 2/2 + gz )out -δW net = dE cv推进功的表达式推进功（流动功、推挤功）A Flow workppW推= p A d l= pVVw推= pvdl注意：不是pdvv 没有变化对推进功的说明、与宏观流动有关，流动停止，推进功不存在1、与宏观流动有关，流动停止，推进功不存在2、作用过程中，工质仅发生位置变化，无状态变化＝pv与所处状态有关，是状态量3、w推4、并非工质本身的能量（动能、位能）变化引起，而由外界（泵与风机）做出，流动工质所携带的能量而由外界（泵与风机）做出流动工质所携带的能量可理解为：由于工质的进出，外界与系统之可理解为由于工质的进出外界与系统之间所传递的一种机械功，表现为流动工质进出系统使所携带和所传递的一种能量开口系能量方程的推导iu pv in inδm δW netgz inin1δm u 22in c δQout out pv out21c gz outδQ + δm in (u + c 2/2 + gz )in 2out -δm out (u + c 2/2 + gz )out -δW net= d E cv开口系能量方程微分式δQ + δm in (u + pv +c 2/2 + gz )in -δW net -δm out (u + pv +c 2/2 + gz )out = d E cv工程上常用流率Q δ•⎛⎞m δ•⎛⎞W δ•⎛⎞0lim Q δτδτ→=⎜⎟⎝⎠0lim m δτδτ→=⎜⎟⎝⎠0lim W δτδτ→=⎜⎟⎝⎠()2cv outd //2outQ E u pv c gz m δτ••=++++2/2u pv c gz m W••−++++()in netinp g开口系能量方程微分式当有多条进出口当有多条进出口：••netcv d /Q E Wδτ=+()2outout/2u pv c gz m •++++∑2•−+++()inin/2u pv c gz m ∑流动时总一起存在流动时，总一起存在焓Enthalpy 的引入定义焓=+定义：焓h = u + pv••netcv d /Q E Wδτ=+()2outout /2u pv c gz m •++++∑h 2u •−+++h ()inin/2pv c gz m ∑开口系能量方程焓Enthalpy的说明h u+ pv[ kJ/kg ]定义：=+[kJ/kg]H= U+ pV[ kJ ]1、焓是状态量state property=)=2、H为广延参数H=U+pV= m(u+pv)= mhh为比参数3、对流动工质，焓代表能量(热力学能+推进功)对静止工质，焓不代表能量4、物理意义：开口系中随工质流动而携带的、取决于热力状态的能量。
