5-4 生活中的常量与变量 课件 (青岛版七年级上)
- 格式:ppt
- 大小:854.50 KB
- 文档页数:16

例谈求函数自变量的取值范围易错点确定函数自变量的取值范围是研究函数时常遇到的问题,可有些同学由于思考不全面等原因,往往出现顾此失彼的错误。
一、只考虑部分,而忽视了整体例1、求函数y=45-+x x 的自变量x 的取值范围。
错解:由x+5≥0,得自变量x 的取值范围是x≥-5。
错解分析:错解中只考虑了使5+x 这部分有意义;而忽视了41-x 有意义的条件,即x-4≠0.正确解法:欲使函数y=45-+x x 有意义,则 解得 x≥-5,且x≠4.所以此函数自变量的取值范围是x≥-5且x≠4.二、只考虑了整体,而忽视了部分例2、求函数y=123--+x x 的自变量的取值范围错解:由2-x -1≠0,即2-x ≠1,解得x≠3.错解分析:错解中忽视了使2-x 这部分有意义时x 的取值。
正确解法:欲使函数y=123--+x x 有意义,则⎩⎨⎧≠--≥-01202x x 解得 x≥2且x≠3。
所以此函数自变量的取值范围是x≥2且x≠3。
三、只考虑一部分,而忽视了另一部分例3、求函数y=1312-++--x xx 的自变量x 的取值范围 错解:由-3+x≠0, 解得自变量x 的取值范围是x≠3 错解分析:错解中只考虑了x x +--312这一部分有意义的条件,而忽视了使2-x 这部分有意义时x 的取值。
⎩⎨⎧≠-≥+0405x x正解:要使函数y=1312-++--x xx 有意义,则 ⎩⎨⎧≥-≠+-0103x x 解得:x≥1且x ≠3 四、只考虑解析式有意义,而忽视了问题本身的意义.例4、等腰三角形的周长为20cm ,若设一腰为x cm ,写出底边y(cm)与腰长x (cm )的函数解析式,并求出自变量x 的取值范围.错解:y 与 x 的函数解析式为y=20-2x,自变量x 的取值范围是全体实数.错解分析:错解中只考虑了20-2x 有意义的条件,而忽视了问题本身的几何意义. 正解:y 与 x 的函数解析式为y=20-2x∵x>0 , y>0,又由三角形任意两边之和大于第三边,可得到不等式组⎪⎩⎪⎨⎧->+>->x x x x x 22002200 解得:5<x<10.所以函数自变量x 的取值范围是:5<x<10.试试看:1.求下列函数自变量x 的取值范围.(1) (2)x x y --+=215 (3)65232+--=x x x y (4)1)1(0+-=x x y 2.小丽拿3元钱去买作业本,已知每本作业本0.25元,试写出县里所剩钱y(元) 与 本数x 之间的函数关系式.并求出自变量x 的取值范围. 653--=x x y。


变量与函数知识点知识点1:变量与常量1.变量:在某一变化过程中,可以取不同值的量叫做变量.2.常量:在某一变化过程中,保持同一数值的量或数,叫做常量或常数.提醒:常量与变量是相对的,要注意判断的前提是“在某一变化过程中”,同一个量在不同过程中是不同的,如在行程问题s=vt中,若s一定,则v、t是变量;若v一定,则s、t 是变量.知识点2:函数1.函数概念:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯—确定的值与其对应.那么我们就说x是自变量,y是x的函数.当x=a 时y=b,那么b叫自变量取a时的函数值.2.函数定义包括的三个要素:一是自变量的取值范围;二是两变量之间对应法则;三是后一个变量被唯一确定而形成的变化范围.例1 下列变量之间的关系不是函数关系的是()A.长方形的宽一定,其长与面积B.正方形的周长与面积C.等腰三角形的底边与面积D.球的体积与球的半径分析:判断变量之间的关系是否存在着函数关系,首先看是否有两个变量,然后再看这两个变量是否是一对一的关系.A项中,长方形的宽一定,它是常量,而面积=长×宽,长与面积是两个变量,若长改变,则面积也变,故A项是函数关系;B项中,正方形的周长与面积是两个变量,给出一个周长的值,除以4就是边长,再平方与面积相对应,故B项是函数关系;C 项中,底边与面积虽是两个变量,但面积公式中还有底边上的高,而这里的高也是变量,这样就有三个变量了,因此C项不是函数关系;D项中,球的体积与其半径是函数关系.答案为C.知识点3:自变量的取值范围1.函数自变量的取值范围的确定必须考虑两个方面:首先,自变量的取值必须使函数解析式有意义;其次,自变量的取值必须使实际问题有意义.2.使函数解析式有意义的代数式类型可归纳为:⑴整式的自变量取全体实数;⑵分式的自变量必须保证分母不为零;⑶根式的自变量取值,偶次根式的被开方数为非负数,而奇次分式的被开方数是一切实数;⑷0指数幂和负指数次2 幂的底数不得为零.例2 函数13+-=x x y 的x 的取值范围是_______. 分析:①偶次根式的被开方数为非负数,故x-3≥0, ②分式的分母不为零,故x+1≠0.由题意得⎩⎨⎧≠+≥-0103x x ,所以x≥3.。





2019-2020年七年级数学上册 5.4 生活中的常量与变量(新版)青岛版教学目标:1.在具体情景中了解常量、变量的概念,能根据具体情况,用关系式表示变量之间的关系。
2.经历探索具体情境中常量及变量之间的关系过程,进一步发展符号感和抽象思维。
3.通过变量、常量的学习,尝试探索变量之间的对应关系,体验客观世界中的运动和变化。
重点:用关系式表示变量之间的关系。
难点:区分具体问题中的常量、变量教材分析:教学方法:教学环节(板书设计): 本节知识树:教学反思一、课前准备温故知新:自学课本教材的相关内容,知道常量和变量的概念,会用关系式表示变量之间的关系。
二、课内探究创设情境:一辆汽车以60千米/小时的速度匀速行驶,行驶里程为s千米.•行驶时间为t 小时.(1).请同学们根据题意填写下表:(2).在以上这个过程中,变化的量是________.不变的量是__________.(3).试用含t的式子表示s.2.请写出下列问题中的常量与变量;将一根长60厘米的铁丝折成一个矩形框架,矩形的长y与宽x之间的关系为y=________________其中常量为____________变量为_________________交流展示:活动一通过做这2个题目,你认为怎样找出问题中的常量与变量?巩固提升:1、一般地说,在一个变化过程中,可以取不同数值的量叫做_________ ,只取同一数值的量叫做___________。
2、在S= r2中,__________是常量,_______________是变量。
3.在圆的周长公式C=2R中,________是常量,_______是变量。
达标检测:1.每张电影票售价为10元,如果早场售出票150张,日场售出205张,晚场售出310张.三场电影的票房收入各多少元.设一场电影售票x张,票房收入y元.•怎样用含x的式子表示y?2.一根弹簧原长12cm,它能挂的质量不超过20kg,并且每挂重1kg就伸长0.5cm,•求:挂重后弹簧的长度y(cm)与挂重x(kg)之间的关系式。

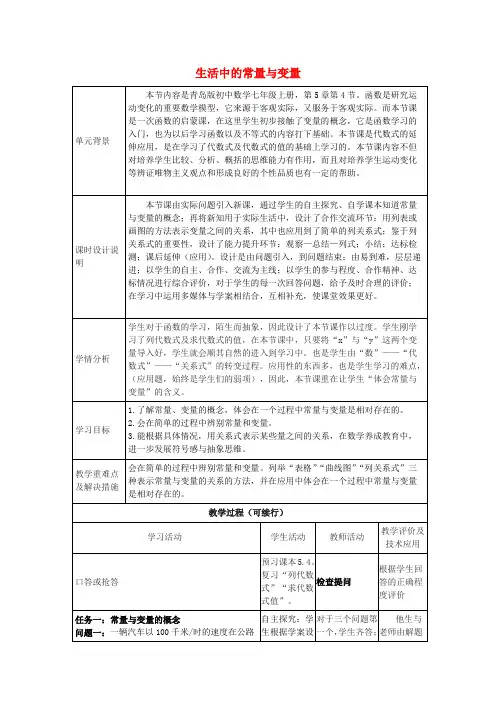
生活中的常量与变量1.5 x上行驶,路程为s (千米),行驶时间为t (时)。
用含有t 的代数式表示s ,s=_______。
保持不变的量是 ,可以取不同的数值的量是 。
问题二:某种杂志每册定价5.80元,买3册应付款 元;买5册应付款____元;如果买x 册,应付款y 元,那么y 用关于x 的代数式表示y=_______.保持不变的量是 ,可以取不同的数值的量是 。
问题三:一个长方形的推拉窗,窗扇高1.5米,如果活动窗扇拉开的距离为x 米,活动窗扇拉开后的通风面积为y 平方米,那么y 用关于x 的代数式表示为y=_______.保持不变的量是 ,可以取不同的数值的量是 。
【概念】:在一个问题中,我们把保持不变的量叫做 ,把可以取不同的数值的量称为 。
计的三个问题,进行自主学习,独立完成题目(都是前面常见的应用问题,相信学生能完成)。
然后结合课本,自己知道并掌握:常量与变量的概念。
并能指出三个问题中的常量与变量。
第二个、第三个一数列为顺序没人回答一空。
对常量与变量的概念的理解,自由回答。
的正确性作评价。
老师根据学生的勇于回答问题的精神、正确程度分别评价。
试一试指出下列事件中的常量与变量 1.电费y(元)与用电量x(千瓦时)之间的关系式为y=0.54x.其中常量是 __, 变量是 。
2.某种报纸每份为固定值a 元,购买x 份此种报纸共需y 元,则y =ax.其中的常量是 ,变量是 。
3.长方形的长和宽分别是a 与b ,则面积s=ab, 其中常量是 ,变量是 ;当长a 是一定值时,s=ab 中,常量是 ,变量是 。
4.圆的面积s 与半径r 之间的关系式为s=πr 2 ,其中常量是 ,变量是 。
5.假设钟点工的工作标准为6元/时,设工作时数为t ,应得工资额为m ,则m=6t ,其中常量是 ,变量是 ____。
对概念的进一步理解。
在问题中发现:1.常量和变量是对某一变化过程来说,不是绝对而是相对的.2.字母不一定都是变量。