简谐近似和简正坐标
- 格式:ppt
- 大小:223.00 KB
- 文档页数:10








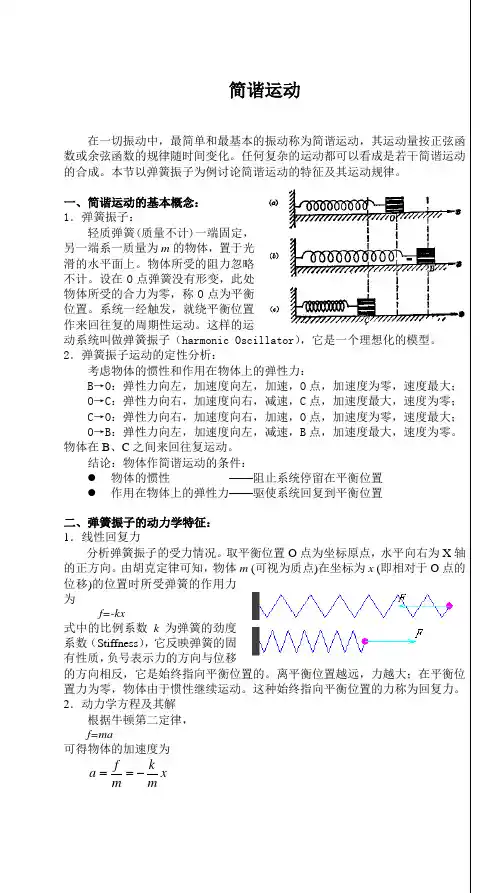
简谐运动在一切振动中,最简单和最基本的振动称为简谐运动,其运动量按正弦函数或余弦函数的规律随时间变化。
任何复杂的运动都可以看成是若干简谐运动的合成。
本节以弹簧振子为例讨论简谐运动的特征及其运动规律。
一、简谐运动的基本概念: 1.弹簧振子:轻质弹簧(质量不计)一端固定,另一端系一质量为m 的物体,置于光滑的水平面上。
物体所受的阻力忽略不计。
设在O 点弹簧没有形变,此处物体所受的合力为零,称O 点为平衡位置。
系统一经触发,就绕平衡位置作来回往复的周期性运动。
这样的运动系统叫做弹簧振子(harmonic Oscillator ),它是一个理想化的模型。
2.弹簧振子运动的定性分析:考虑物体的惯性和作用在物体上的弹性力:B →O :弹性力向左,加速度向左,加速,O 点,加速度为零,速度最大; O →C :弹性力向右,加速度向右,减速,C 点,加速度最大,速度为零; C →O :弹性力向右,加速度向右,加速,O 点,加速度为零,速度最大; O →B :弹性力向左,加速度向左,减速,B 点,加速度最大,速度为零。
物体在B 、C 之间来回往复运动。
结论:物体作简谐运动的条件:● 物体的惯性 ——阻止系统停留在平衡位置 ● 作用在物体上的弹性力——驱使系统回复到平衡位置二、弹簧振子的动力学特征: 1.线性回复力分析弹簧振子的受力情况。
取平衡位置O 点为坐标原点,水平向右为X 轴的正方向。
由胡克定律可知,物体m (可视为质点)在坐标为x (即相对于O 点的位移)的位置时所受弹簧的作用力为f=-kx式中的比例系数k 为弹簧的劲度系数(Stiffness ),它反映弹簧的固有性质,负号表示力的方向与位移的方向相反,它是始终指向平衡位置的。
离平衡位置越远,力越大;在平衡位置力为零,物体由于惯性继续运动。
这种始终指向平衡位置的力称为回复力。
2.动力学方程及其解根据牛顿第二定律, f=ma可得物体的加速度为x mk m f a -==0202x v v x ωω-⎪⎭⎫⎝⎛+=2020⎪⎭⎫ ⎝⎛+ωv x =求02.072.0=m k =v x 6004.022222020+=+=ω2=4π±,由(4π-。
第五章思考题5・1虚功原理中的“虚功”二字作何解释?用虚功原理理解平衡问题,有何优点和缺点?5.2为什么在拉格朗日方程中,&不包含约束反作用力?又广义坐标与广义力的含义如a何?我们根据什么关系由一个量的量纲定岀另一个量的量纲?5. 3广义动量几和广义速度么是不是只相差一个乘数川?为什么p a比么更富有意义?5.4既然乞是广义动量,那么根据动虽泄理,乞|旦]是否应等于广义力0 ?为什么瓯dt [ dq a J a在拉格朗日方程(5.3.14)式中多岀了三项?你能说出它的物理意义和所代表的物理量吗?5. 5为什么在拉格朗日方程只适用于完整系?如为不完整系,能否由式(5.3」3)得出式(5314)?5. 6平衡位置附近的小振动的性质,由什么来决泄?为什么2疋个常数只有2s个是独立的?5. 7什么叫简正坐标?怎样去找?它的数目和力学体系的自由度之间有何关系又每一简正坐标将作怎样的运动?5. 8多自由度力学体系如果还有阻尼力,那么它们在平衡位宜附近的运动和无阻尼时有何不同?能否列岀它们的微分方程?5.9 d厶和〃兀有何区别?仏和匹有何区别?5. 10哈密顿正则方程能适用于不完整系吗?为什么?能适用于非保守系吗?为什么?5. 11哈密顿函数在什么情况下是整数?在什么情况下是总能量?试祥加讨论,有无是总能量而不为常数的情况?5. 12何谓泊松括号与泊松泄理?泊松左理在实际上的功用如何?5. 13哈密顿原理是用什么方法运动规律的?为什么变分符号§可置于积分号内也可移到积分号外?又全变分符号△能否这样?5. 14正则变换的目的及功用何在?又正则变换的关键何在?5. 15哈密顿-雅可比理论的目的何在?试简述次理论解题时所应用的步骤.5.16正则方程(5.5.15)与(5」0.10)及(5.10」1)之间关系如何?我们能否用一正则变换由前者得岀后者?5. 17在研究机械运动的力学中,刘维立理能否发挥作用?何故?5.18分析力学学完后,请把本章中的方程和原理与牛顿运动左律相比较,并加以评价.第五章思考题解答5.1答:作•用于质点上的力在任意虚位移中做的功即为虚功,而虚位移是假想的、符合约束的、无限小的•即时位置变更,故虚功也是假想的、符合约束的、无限小的•且与过程无关的功,它与真实的功完全是两回事•从別V =艺庁•另可知:虚功与选用的坐标系无关,这/正是虚功与过程无关的反映;虚功对各虚位移中的功是线性迭加,虚功对应于虚位移的一次变分•在虚功的计算中应注意:在任意虚过程中假左隔离保持不变,这是虚位移无限小性的结果.虚功原理给出受约朿质点系的平衡条件,比静力学给岀的刚体平衡条件有更普遍的意义;再者,考虑到非惯性系中惯性力的虚功,利用虚功原理还可解决动力学问题,这是刚体力学的平衡条件无法比拟的:另外,利用虚功原理解理想约束下的质点系的平衡问题时,由于约束反力自动消去,可简便地球的平衡条件;最后又有广义坐标和广义力的引入得到广义虚位移原理,使之在非纯力学体系也能应用,增加了其普适性及使用过程中的灵活性•由于虚功方程中不含约朿反力•故不能求出约束反力,这是虚功原理的缺点•但利用虚功原理并不是不能求出约束反力,一般如下两种方法:当刚体受到的主动力为已知时,解除某约束或某一方向的约束代之以约束反力:再者,利用拉格朗日方程未定乘数法,景观比较麻烦,但能同时求出平衡条件和约束反力.5.2答因拉格朗日方程是从虚功原理推岀的,而徐公原理只适用于具有理想约朿的力学体系虚功方程中不含约朿反力,故拉格朗日方程也只适用于具有理想约束下的力学体系,O a不含约束力;再者拉格朗日方程是从力学体系动能改变的观点讨论体系的运动,而约束反作用力不能改变体系的动能,故不含约束反作用力,最后,几何约束下的力学体系其广义坐标数等于体系的自由度数,而几何约束限制力学体系的自由运动,使其自由度减小,这表明约束反作用力不对应有独立的广义坐标,故匕不含约束反作用力•这里讨论的是完整系的拉格朗日方程,对受有几何约朿的力学体系既非完整系,则必须借助拉格朗日未泄乘数法对拉格朗日方程进行修正.广义坐标市确立质点或质点系完整的独立坐标,它不一泄是长度,可以是角度或其他物理量,如而积、体积、电极化强度、磁化强度等•显然广义坐标不一迫是长度的量纲•在完整约束下,广义坐标数等于力学体系的自由度数:广义力明威力实际上不一泄有力的量纲可以是力也可以是力矩或其他物理量,如压强、场强等等,广义力还可以理解为:若让广义力对应的广义坐标作单位值的改变,且其余广义坐标不变,则广义力的数值等于外力的功由f斤.輕=£乞&& =宓知,乙冈a有功的量纲,据此关系已知其中一个量的量纲则可得到另一个量的量纲•若0a是长度,则一左是力,若乞是力矩,则%一泄是角度,若%是体积,则乞一定是压强等.5.3答与不一泄只相差一个常数川,这要由问题的性质、坐标系的选取形式及广义坐标的选用而左。
考点二 简谐运动的公式和图像2.简谐运动的公式和图像(1)表达式①动力学表达式:F =-kx ,其中“-”表示回复力与位移的方向相反. ②运动学表达式:x =A sin(ωt +φ0),A 表示简谐运动的振幅,ω是一个与周期成反比、与频率成正比的量,叫做简谐运动的“圆频率”,表示简谐运动的快慢,ω=2πT =2πf 。
φ0叫做初相,ωt +φ0代表简谐运动的相位。
2.图象①从平衡位置开始计时,函数表达式为x =A sin ωt ,图象如图1甲所示.②从最大位移处开始计时,函数表达式为x =A cos ωt ,图象如图乙所示.1.对简谐运动图象的认识图14-1-7(1)简谐运动的图象是一条正弦或余弦曲线,如图14-1-7所示.(2)图象反映的是位移随时间的变化规律,随时间的增加而延伸,图象不代表质点运动的轨迹.2.图象信息(1)由图象可以得出质点做简谐运动的振幅、周期和频率.(2)可以确定某时刻质点离开平衡位置的位移.(3)可以确定某时刻质点回复力、加速度的方向:因回复力总是指向平衡位置,故回复力和加速度在图象上总是指向t 轴.(4)确定某时刻质点速度的方向:速度的方向可以通过下一时刻位移的变化来判定,下一时刻位移如增加,振动质点的速度方向就是远离t 轴;下一时刻位移如减小,振动质点的速度方向就是指向t 轴.(5)比较不同时刻回复力、加速度的大小.(6)比较不同时刻质点的动能、势能的大小.【典例1】(多选)某质点做简谐运动,其位移随时间变化的关系式为x =A sinπ4t ,则关于该质点,下列说法正确的是( )A.振动的周期为8 sB.第1 s 末与第3 s 末的位移相同C.第1 s 末与第3 s 末的速度相同D.第3 s 末至第5 s 末的位移方向都相同E.第3 s 末至第5 s 末的速度方向都相同解析 由关系式可知ω=π4 rad/s ,T =2πω=8 s ,选项A 正确;将t =1 s 和t =3 s 代入关系式中求得两时刻位移相同,选项B 正确;作出质点的振动图象,由图象可以看出,第1 s 末和第3 s 末的速度方向不同,选项C 错误;由图象可知,第3 s 末至第4 s 末质点的位移方向与第4 s 末至第5 s 末质点的位移方向相反,而速度的方向相同,故选项D 错误,E 正确。