当前位置：文档之家 › 固体物理第四章总结1

固体物理第四章总结1

  • 格式：doc
  • 大小：321.50 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

固体物理学：4-1 布洛赫定理

固体物理学：4-1 布洛赫定理
§4-1 布洛赫定理
一. 布洛赫定理
一个在周期场中运动的电子的波函数应具 有哪些基本特点？
在量子力学建立以后，布洛赫（F.Bloch）和 布里渊（Brillouin）等人就致力于研究周期场 中电子的运动问题。他们的工作为晶体中电子 的能带理论奠定了基础。
布洛赫定理指出了在周期场中运动的电子 波函数的特点。
4 根据周期性边界条件求本征值 周期性边界条件
对于 对于 对于
—— 整数
—— 引入矢量 满足
—— 倒格子基矢
平移算符的本征值
5 Bloch 定理的证明 平移算符的本征值
将
作用于电子波函数
电子的波函数 满足布洛赫定理
—— 布洛赫定理 —— 布洛赫函数 —— 晶格周期性函数
三、 平移算符本征值的物理意义
注：由于德布洛意关系
P h
，即
P
k
，
所以 k 空间也称为动量空间。
kx
2
L
nx
(nx 0,1,2,)
上式告诉我们，沿 k 空间的每个坐标轴方向，
电子的相邻两个状态点之间的距离都是 因此，k 空间中每个状态点所占的体积为
2
L
2 L
图 3 表示二维 k 空间每个点所占的面积是
ky
2
。
3
1、一维情况的布洛赫定理
在一维情形下，周期场中运动的电子能量E(k)
和波函数 k ( x) 必须满足定态薛定谔方程
2 2m
d2 dx 2
V ( x)
k(x) E(k)k(x)
(1)
k -------表示电子状态的角波数 V( x ) ----周期性的势能函数，它满足
V( x ) = V( x + n a ) a ---- 晶格常数 n -----任意整数

固体物理 04-01布洛赫定理

固体物理 04-01布洛赫定理

大
学
Solid State Physics
固
体
物
理
—— 布洛赫定理
为一矢量 —— 当平移晶格矢量
—— 波函数只增加了位相因子 电子的波函数
—— 布洛赫函数
西
南 晶格周期性函数
科 技 大 学
—— 晶格周期性函数
Solid State Physics
固 体 物
理 布洛赫定理的证明
—— 引入平移算符 证明平移算符与哈密顿算符对易 两者具有相同的本征函数
二十年代初期，在用量子力学研究金属
的电导理论的过程中发展起来的。
西 南 科 技 大 学
Solid State Physics
固
体
物
理
Felix Bloch，1905.10 – 1983.9
博士论文《金属的传导理论》
发展核磁精密测量的新方法及其有 关的发现，与爱德华·珀塞尔（ Edward Mills Purcell, 1912-1997） 分享 1952年诺贝尔物理学奖
Solid State Physics
固 体
物 平移算符本征值的物理意义
理
1)
—— 原胞之间电子波 函数相位的变化
2) 平移算符本征值量子数
西
南 —— 简约波矢，对应于平移动操作本征值的量子数
科
技 —— 不同的简约波矢，原胞之间的相位差不同
大 学
Solid State Physics
固
体
物
理
—— 布洛赫定理
？
b）晶体中电子的平均自由程为什么会远大于
西
南 原子的间距？
科
技 大
……
学
Solid State Physics

黄昆 固体物理 讲义 第四章

黄昆 固体物理 讲义 第四章

KK
KK
KK K K K K T1ψ ( r ) = ψ ( r + a1 ) = eik ⋅a1ψ ( r )
ψ ( r ) 和ψ ( r + a1 ) 分别是相邻两个原胞中电子的波函数 —— 两者只相差一个位相因子 λ1 = eik ⋅a
K
K
K
K
KK
1
，不同的简 2）平移算符本征值量子数： k 称为简约波矢（与电子波函数的波矢有区别，也有联系） 约波矢，原胞之间的位相差不同。 3）如果简约波矢改变一个倒格子矢量： Gn = n1b1 + n 2 b2 + n3b3 ， n1 , n 2 , n3 为整数。
-3-
CREATED BY XCH
固体物理学_黄昆_第四章 能带理论_20050404
由于存在对易关系，根据量子力学可以选取 H 的本征函数，使它同时成为各平移算符的本征函数。
有：
Hψ = Eψ T1ψ = λψ ψ = λ2ψ , T3ψ = λ3ψ 1 , T2
本征值的确定： λ1 , λ2 , λ3
KK ik ⋅a1
则平移算符 T1 , T2 , T3 的本征值可以表示为： λ1 = e
, λ2 = e ik ⋅a2 , λ3 = e ik ⋅a3
KK
KK
将 T ( Rm ) = T1 1 ( a1 )T2 2 ( a 2 )T3 3 ( a 3 ) 作用于电子的波函数ψ ( r )
m m m
K K K
K
K
K
( 2π ) 3 Ω
固体物理学_黄昆_第四章 能带理论_20050404
第四章 能带理论
能带理论是目前研究固体中电子运动的一个主要理论基础． 在二十世纪二十年代末和三十年代初期， 在量子力学运动规律确立以后，它是在用量子力学研究金属电导理论的过程中开始发展起来的．最 初的成就在于定性地阐明了晶体中电子运动的普遍性的特点。 —— 说明了固体为什么会有导体、非导体的区别 —— 晶体中电子的平均自由程为什么会远大于原子的间距……等 —— 能带论为分析半导体提供了理论基础，有力地推动了半导体技术的发展 —— 大型高速计算机的发展， 使能带理论的研究从定性的普遍性规律发展到对具体材料复杂能带结 构的计算 能带理论是一个近似的理论．在固体中存在大量的电子。它们的运动是相互关联着的，每个电子的 运动都要受其它电子运动的牵连，这种多电子系统严格的解显然是不可能的．能带理论是单电子近 似的理论，就是把每个电子的运动看成是独立的在一个等效势场中的运动．在大多数情况下，人们 最关心的是价电子，在原子结合成固体的过程中价电子的运动状态发生了很大的变化，而内层电子 的变化是比较小的，可以把原子核和内层电子近似看成是一个离子实．这样价电子的等效势场，包 括离子实的势场，其它价电子的平均势场以及考虑电子波函数反对称性而带来的交换作用．单电子 近似最早用于研究多电子原子，又称为哈特里（Hartree）－福克（ΦOK）自洽场方法。 能带理论的出发点是固体中的电子不再束缚于个别的原子，而是在整个固体内运动，称为共有化电 子．在讨论共有化电子的运动状态时假定原子实处在其平衡位置，而把原子实偏离平衡位置的影响 看成微扰，对于理想晶体，原子规则排列成晶格，晶格具有周期性，因而等效势场 V(r)也应具有周 期性．晶体中的电子就是在一个具有晶格周期性的等效势场中运动，

固体物理_第4章_能带理论

固体物理_第4章_能带理论

ik ( r R n ) u ( r Rn ) e u (r )
u ( r ) ，代入上式有：
(2 )
则：u (r Rn ) u (r )
即布洛赫波是振幅受到具有同晶格周期相同的周期性函数调制的平面 波。
ˆ ( R ) H HT ( R ) 0 ˆ ˆˆ T n n
根据量子力学知识可知：哈密顿量和平移算符有共同的本征态，可选 择哈密顿量的本征态 (r ) 为共同本征态。
采用波恩-卡曼周期性边界条件有： N ˆ ˆ ˆ ˆ (r ) (r N1a1 ) T ( N1a1 ) (r ) T (a1 )T (a1 )T (a1 ) (r ) 1 1 (r )
，而内层电子的变化较小，可以把内层电子和原子实近似看成离子实 这样价电子的等效势场包括离子实的势场，其他价电子的平均势场以 及电子波函数反对称性而带来的交换作用。 能带理论是单电子近似理论，即把每个电子的运动看成是独立的 在一个等效势场中的运动。单电子近似理论最早用于研究多电子原子
，又称为哈特里（Hartree）-福克（o ）自洽场方法。 把多体问题简化为单电子问题需要进行多次简化。1、绝热近似： 原子核或者离子实的质量比电子大的多，离子的运动速度慢，在讨论 电子问题时可以认为离子是固定在瞬时位置上。这样多种粒子的多体 问题就简化为多电子问题；
能带理论取得相当的成功，但也有他的局限性。如过渡金属化 合物的价电子迁移率较小，相应的自由程和晶格常数相当，这时不 能把价电子看成共有化电子，周期场的描述失去意义，能带理论不 再适用。此外，从电子和晶格相互作用的强弱程度来看，在离子晶 体中的电子的运动会引起周围晶格畸变，电子是带着这种畸变一起 前进的，这些情况都不能简单看成周期场中单电子运动。

固体物理学：第四章总结

固体物理学：第四章总结
2
(r
ki
Rn)
bi 2
eik
，(i
Rn
(r ),
1，2 ，3 )
(r ) (r )
k
kKh
在此范围内k共有N个值(N为晶体原胞数) 。
近自由电子近似
1.模型： 假定周期场起伏较小，而电子的平均动能比其势
能的绝对值大得多。作为零级近似，用势能的平均值V0代替
V(x)，把周期性起伏V(x)-V0作为微扰来处理。
Rs
5.能带宽度： E Emax Emin
费米面的构造法
1.画出布里渊区的广延区图形；
2.画出自由电子费米面(费米面的广延区图)；
N
kF
Z(k )dk
0
kF 0
2N A
2πkdk
πk
2 F
2N A
kF
A
1
2
2π
3.将落在各个布里渊区的费米球片断平移适当的倒格矢进
入简约布里渊区中等价部位；
3.结论：
发生能量不连续的波矢 k 满足的条件可改写为:
Kn
(k
Kn 2
)
0
k'
k
Kn
0
Kn
对于三维的情况，沿各个方向在布里渊区边界E(k)函数是 间断的，但不同方向断开时的能量取值不同，因而有可能使能 带发生重叠。
紧束缚近似
1.模型
晶体中的电子在某个原子附近时主要受该原子势场V
(r
Rm
)
的作用，其他原子的作用视为微扰来处理，以孤立原子的电子
态作为零级近似。
2.势场
V r V (r Rm )
'V
(r
Rn
)

固体物理各章节知识点详细总结

固体物理各章节知识点详细总结

3.1 一维晶格的振动
3.1.1 一维单原子链的振动
1. 振动方程及其解 (1)模型：一维无限长的单原子链，原子间距(晶格常量)为
a，原子质量为m。
模型 运动方程
试探解
色散关系
波矢q范围 B--K条件
波矢q取值
一维无限长原子链，m，a，
n-2 n-1 n mm
n+1 n+2
a
..
m x n x n x n 1 x n x n 1
x M 2 n x 2 n 1 x 2 n 1 2 x 2 n
..
x m 2n1 x 2 n 2 x 2 n 2 x 2 n 1
x
Aei2n1aqt
2 n1
x
Bei2naqt
2n
相隔一个晶格常数2a的同种原子，相位差为2aq。
色散关系
2co as q A M 22B0 m 22A 2co as q B0
a h12 h22 h32
由
2π Kh
d h1h2h3
2π
d K 得： h1h2h3
h1h2h3
简立方：a 1 a i,a 2 aj,a 3 a k ,
b12πa2a3 2πi
Ω
a
b22πa3a1 2πj
Ω
a
b32πa1a2 2πk
Ω
a
b1 2π i a
b2 2π j a
2π b3 k
2n-1
2n
2n+1
2n+2
M
m
质量为M的原子编号为2n-2 、2n、2n+2、···
质量为m的原子编号为2n-1 、2n+1、2n+3、···

固体物理各章节重点总结

固体物理各章节重点总结

固体物理各章节重点总结第一章1、晶体的共性：长程有序、自限性、各向异性2、长程有序：晶体中的原子都是按照一定规则排列的，这种至少在微米数量级范围内的有序排列，称为长程有序。

3、自限性：晶体具有自发地形成封闭几何多面体的特性。

4、原子之间的结合遵从能量最小原理5、一个原子周围最近邻的原子数，称为该晶体的配位数，用来表征原子排列的紧密程度，最紧密的堆积称密堆积6、布喇菲提出了空间点阵学说：晶体内部结构可以看成是由一些相同的点子在空间做规则的周期性的无线分布。

这一学说是对实际晶体结构的一个数学抽象，它只反映出晶体结构的周期性。

人们把这些点子的总体称为布喇菲点阵7、沿三个不同方向通过点阵中的结点作平行的直线，把结点包括无遗，点阵便构成一个三维网格。

这种三维格子称为晶格，又称为布喇菲格子，结点又称点阵。

8、某一方向上两相邻结点的距离为该方向上的周期，以一结点为顶点，以三个不同方向的周期为边长的平行六面体可作为晶格的一个重复单元，体积最小的重复单元，称为原胞或固体物理学原胞，它能反映晶格的周期性。

9、为了同时反映晶体对称的特征，结晶学上所取的重复单元，体积不一定最小，结点不仅在顶角上，还可以是体心或面心。

这种重复单元称作晶胞，惯用晶胞或布喇菲原胞10、简立方：a1=a，a2=b,a3=c11、体心立方：a1=0.5(-a+b+c)|a2=0.5(a-b+c)|a3=0.5(a+b-c)12、面心里放：a1=0.5(b+c)|a2=0.5(a+c)|a3=0.5(a+b)|13、氯化铯结构为简立方结构14、氯化钠结构为面心立方结构15、金刚石结构为面心立方结构16、所欲格点都分布在相互平行的一平面族上，每一平面都有格点分布，称这样的平面为晶面17、若ij=1,2…则可用正格基失来构造倒格基失18、将正格基失在空间平移可构成正格子，相应地我们把倒格基失平移形成的格子叫做倒格子19、正格原胞体积与倒格原胞体积之积等于(2π)3；正格子与倒格子互为多方的倒格子；倒格失K h=h1b1+h2b2+h3b3与正格子晶面族正交；倒格失的模K h与晶面族(h1h2h3)的面间距成反比20、晶体有230种对称类型，称其为空间群；若不包括平移，有32种宏观对称类型，称其为点群21、晶体的宏观对称操作一共有八种基本对称操作P1922、计算题P25P34第二章1、五种基本结合类型：共价结合、离子结合、金属结合、分子结合、氢键结合2、体积弹性模量3、计算题P53P63第三章1、玻恩和卡门提出了一个遐想的边界条件，即所谓的周期性边界条件。

固体物理知识点总结 第四章

固体物理知识点总结 第四章
第四章 金属自由电子理论 总
电子气的热容量 功函数和接触电势差
结
自由电子气的能量状态
自由电子气的能量状态
一、自由电子气的能量状态 1.自由电子气(自由电子费米气体)：是指自由的、无相互 ：是指自由的、 作用的、遵从泡利原理的电子气。 作用的、遵从泡利原理的电子气。 2.自由电子气的能量
2πnx kx = L ; 2πny ; ky = L k = 2πnz ; z L
−( E0 −EF )
4πem j＝ 3 (kBT)2 e h
3.接触电势
kBT
= AT e
2 −ϕ kBT
两块不同的金属A 两块不同的金属A和Ｂ相接触，或用导线连接起来，两块 相接触，或用导线连接起来， 金属就会彼此带电产生不同的电势V 称为接触电势。 金属就会彼此带电产生不同的电势 A和VB，称为接触电势。
1 VA − VB = ( ϕ B −43; C = γT + bT
e V a V
3
π2 k２ R 2 B ＝ π Z γ = N0 Z 0 2 EF 2T 0 F
12 Rπ4 b= 3 5 θD
功函数和接触电势差
1.功函数： 电子在深度为E 的势阱内，要使费米面上的电子逃离金属， 电子在深度为 0的势阱内，要使费米面上的电子逃离金属， 的能量， 称为脱出功又称功函数。 至少使之获得ϕ=E0－ＥＦ的能量，ϕ称为脱出功又称功函数。 2.里查逊—德西曼公式
h2k 2 h2 2 2 E= (kx + k 2 + kz ) = y 2m 2m
3.能态密度
∆Z dZ N(E) = lim = E dE ∆E→0 ∆
自由电子气的能态密度
dZ = cE1 2 N(E) = dE

固体物理学第四章

固体物理学第四章
当T0时，CV 0，与实验结果定性符合。 但实验结果表明， T0 ， CV ∝T3; 根据Einstein模型，T0，
0 CV exp 0 kBT
28
Einstein模型 金刚石热容量的实验数据
29
4.6 Debye模型 一、模型
假设：晶体是各向同性的连续弹性介质，格波可以看
l V
1 U (T ) s (q)[ns (q) ] 2 s ,q
色散关系
对于实际晶体，晶格振动波矢的代表点密集的均匀分布于布 里渊区内，因此可引入频率分布函数 ( )， 将上式改写为：
在 附近单位频率间隔内的振动模式的数目
ρ()d ：频率在－＋d之间的振动模式数
0
E 3/2 f ( E )dE
17
才有明显变化，因此 T 0 K 时只有能量在 EF 附近 kBT 范围内 f ( E )
1
(0 E EF kBT )
f ( E)

E EF k BT 2kBT
( EF kBT E EF kBT )
0
( E EF kBT )
1 ( , q) (q)[n( , q) ] 2
与同一波矢 q 相应的角频率 (q ) 可以不止一个——不同的 频支。因此与晶格振动相应的固体的内能为：
1 U (T ) s (q)[ns (q) ] 2 s ,q
23
则晶格振动的定容热容为：
U (T ) C T
与温度有关的内能： 绝缘体 金属
晶格振动能量 晶格振动能量＋价电子的热动能
低温下才考虑
3
4.1 电子气的状态密度
金属的自由电子气Drude模型
4

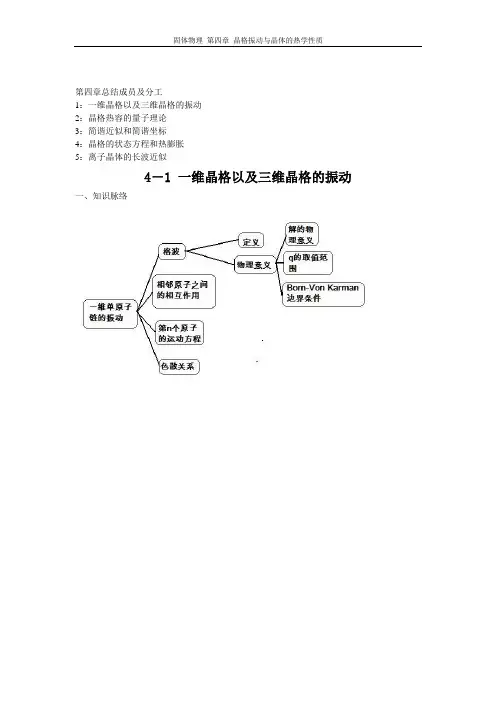
固体物理第四章总结1

固体物理第四章总结1

第四章总结成员及分工1：一维晶格以及三维晶格的振动2：晶格热容的量子理论3：简谐近似和简谐坐标4：晶格的状态方程和热膨胀5：离子晶体的长波近似4－1 一维晶格以及三维晶格的振动一、知识脉络二、重点1.格波的概念和“格波”解的物理意义(1)定义：晶格原子在平衡位置附近作振动时，将以前进波的形式在晶体中传播，这种波称为格波。

(2)物理意义：一个格波解表示所有原子同时做频率为ω的振动，不同原子之间有位相差。

相邻原子之间的位相差为aq 。

(3) q 的取值范围：－(π/a)<q ≤(π／a)这个范围以外的值，不能提供其它不同的波。

q 的取值及范围常称为布里渊区（Brillouin zones ）。

(4) Born-Von Karman 边界条件: 1)(=-Naq i e h Naq ⨯=π22.一维单原子链的色散关系22241[1cos ]sin ()2aq aq m m ββω=-=把 ω 与q 之间的关系称为色散关系(disperse relation)，也称为振动频谱或振动谱。

3.一维单原子链的运动方程相邻原子之间的相互作用βδδ-≈-=d dvF ad v d ⎪⎪⎭⎫ ⎝⎛=22δβ 第n 个原子的运动方程11()(2)n n n n i t naq nq m Ae ωμβμμμμ∙∙+--=+-=4.一维双原子链中两种原子的运动方程及其解（1）运动方程( equation))2(2221212n n n n M μμμβμ---=+++∙∙ )2(2221212n n n n M μμμβμ---=+++∙∙（2）方程的解(solution)])2([2q na t i n Ae -=ωμ ])12([12aq n t i n Be +-+=ωμ5.声学波与光学波的概念与物理意义（1）声学波与光学波的定义}]sin )(41[1{2/1222aq M m mM mM M m +-++=+βω }]sin )(41[1{2/1222aq M m mMmM M m +--+=-βω ω＋对应的格波称为光学波（optic wave ）或光学支（optic branch) ；ω－对应的格波称为声学波(acoustic wave)或声学支（acoustic branch ）（2）两种格波的振幅比aq m A B cos 222ββω--=⎪⎭⎫⎝⎛++aq m A B cos 222ββω--=⎪⎭⎫⎝⎛--（3）ω＋ 与ω－ 都是q 的周期函数)()(q aq --=+ωπω)()(q aq ++=+ωπω其中aq a22ππ≤〈-6.对色散关系的讨论（1）一维单原子链与一维双原子链的格波解的差异一维单原子链只有一支格波（一个波矢对应一个格波）— 声学波；而一维双原子链则有两支格波（一个波矢对应两个格波）— 声学波和光学波，两支格波的频率各有一定的范围：0)0()(min ==--ωω Maβπωω2)2()(max ==-- m aβπωω2)2()(min ==++ mMM m )(2)0()(max +==++βωω 在ω-max 与ω+min 之间有一频率间隙，说明这种频率的格波不能被激发。

固体物理学复习总结

固体物理学复习总结

第一章 晶体结构1.晶体：组成固体的原子（或离子）在微观上的排列具有长程周期性结构；eg ：单晶硅。

晶体具有的典型物理性质：均匀性、各向异性、自发的形成多面体外形、有明显确定的熔点、有特定的对称性、使X 射线产生衍射。

非晶体：组成固体的粒子只有短程序，但无长程周期性；eg ：非晶硅、玻璃准晶：有长程的取向序，沿取向序的对称轴方向有准周期性，但无长程周期性，不具备晶体的平移对称性；eg ：快速冷却的铝锰合金2.三维晶体中存在7种晶系14种布拉菲格子；对于简单格子晶胞里有几个原子就有几个原胞，复式格子中包含两个或更多的格子。

3.典型格子特点：sc bcc fcc hcp Diamond 晶胞体积3a 3a 3a 32a 3a 每晶胞包含的格点数1 2 4 6 8 原胞体积3a 321a 341a 332a 341a 最近邻数（配位数）6 8 12 12 4 填充因子0.524 0.68 0.74 0.74 0.34 典型晶体 NaCl CaO Li K Cu Au Zn Mg Si Ge4.sc 正格子基矢：k a a j a a i a a ===321,,；sc 倒格子基矢：k ab j a i a πππ2,2b ,2b 321===； fcc 正格子基矢：)2),2),2321j i a a k i a a k j a a +=+=+=（（（； fcc 倒格子基矢：)2),2),2b 321k j i ab k j i a b k j i a -+=+-=++-=（（（πππ； bcc 正格子基矢： )2),2),2321k j i a a k j i a a k j i a a -+=+-=++-=（（（； bcc 倒格子基矢：)2),2),2b 321j i a b k i a b k j a +=+=+=（（（πππ； 倒格子原胞基V a a )(2b 321⨯=π，V a a )(2b 132⨯=π，Va a )(2b 213⨯=π 正格子和倒格子的基矢关系为ij a πδ2b j i =⋅；设正格子原胞体积为V,倒格子原胞体积为Vc ，则3)2(V c V π=⨯。

固体物理讲义第四章

固体物理讲义第四章

第四章 晶格振动和晶体的热学性质● 晶格振动：晶体中的原子在格点附近作热振动● 原子的振动以波的形式在晶体传播（原子的振动波称为格波） ● 晶格振动对晶体的性质有重要影响 主要内容● 晶格动力学（经典理论，1912年由波恩和卡门建立）晶格振动的模式数量（有多少种基本的波动解） 晶格振动的色散关系（波动的频率和波数的关系）● 晶格振动的量子理论 ● 固体的热容量 4.1 一维单原子链的振动原子链共有N 个原胞，每个原胞只有一个原子,每个原子具有相同的质量m,平衡时原子间距等于晶格常数a,原子沿链方向运动,第n 个原子离开平衡位置的位移用x n 表示,第n 个原子和第n+1个原子间的相对位移为 一维单原子链原子振动时，相邻两个原子之间的间距: 基本假设● 平衡时原子位于Bravais 格点上 ● 原子围绕平衡位置作微振动●简谐近似：原子间的相互作用势能只考虑到平方项 微振动时：简谐近似：势能展开式保留到二次项微振动：原子离开平衡位置的位移与原子间距相比是小量。

晶体中原子的平衡位置由原子结合能（势）决定。

任何一种晶体，原子间的相互作用势能可以表述成原子之间距离的函数。

n n x x -=+1δδ+=a x ()()⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=+=222 21 )(δδδa ax d U d x d U d a U a U x U把qa改变一个2π的整数倍，原子的振动相同，因此可以把qa限制负pi和正pi之间，此范围以外的q值，并不提供新的物理内容.群速度是指波包的传播速度，dw/dq,也就是能量在介质中的传播速度。

在布里渊区的边界上，群速度为零，波是一个驻波。

4.2 一维双原子链的振动q趋于0时，w也趋于零，称为声学波4.3 三维晶格的振动(略) 一个原胞中有n 个原子晶格基矢： 原胞数目： 原子的质量： 对于一个波矢q,有3n 个ω（即有3n 支色散曲线） 在3n 支色散关系中，当q→0时（长波）：有三支ω →0，且各原子的振幅趋于相同，这三支为声学波。

第四章 第一节 布洛赫定理

第四章 第一节 布洛赫定理

该方程可以在一个正点阵元胞内求解，属于在有 限区域内的厄米本征值问题，应该有无穷多分立 的本征值E n(k)，对应无穷多的本征函数。
2. 对于一个确定的n， 能量本征值和波函
数都是k的周期函数
我们注意到
其中 将
仍然是正点阵的周期函数 代入能量本征值方程，得到
对比
它们完全相同，因此
即
有相同的本征值，即
对所有具有时间反演对称性的晶体能谱有：
由式子4.1.20有
两边取共轭，k -> -k
能量本征值必须是实数：
结果
满足同一方程，有
5. 等能面垂直于布里渊区界面
等能面定义为k空间，所有能量相等的k构成的曲面。
布里渊区界面是K h的中垂面，因此相对于K h 和-K h的一对布里渊区界面有镜面反演对称。 设A，B为布里渊区界面上关于m对称的两个点，a, b为 布里渊区界面上关于m对称的两个点。它们之间正好 相差一个倒格矢K h。 过a,b两点等能面的法线为
这就是布洛赫定理。
当平移晶格矢量R时，同一能量本征值的波函数只增 加一个相位因子。
注意：不是R的周期函数！
布洛赫定理的另一种表达形式： 周期势场中的单电子波函数可以写成一个调幅的 平面波（布洛赫波函数）：
其中调幅因子u满足R的周期性：
很显然，该函数必然满足布洛赫定理
与自由电子波函数相比，周期场的作用只是用一 个调幅平面波取代了平面波，称为布洛赫波。
平移算符
晶体最重要的特征是平移对称性，定义三个基本的 平移算符： 对任一函数：
它们是可对易的：
同时，平移算符 也是可对易的：
与哈密顿
即
这四个算符具有相同的本征函数，可以用它们所对 应的本征值的量子数来标志周期中的单电子态。

孙会元固体物理基础第四章晶格振动和晶体的热性质4.2 长波近似

孙会元固体物理基础第四章晶格振动和晶体的热性质4.2 长波近似

因此恢复力又可写为:
um1 um F c a/2
此外,因第m +1个原子的位移而引起的对第m 个原子产生的恢复力可写为:
F ( u u ) m 1 m
mM 对于一维复式格子,质量密度为： 1 a c 2 v a 弹 2 ( m M )
对于长光学波,用u+表示质量为M的正离子位 移,用u-表示质量为m的负离子位移. 由正、负离子的相对位移所引起的宏观电场 强度设为E.这时,作用在离子上的除了准弹性恢 复力之外,还有电场的作用. 但是,必须注意,作用在某一离子上的电场不能 包括该离子本身所产生的电场. 从宏观电场强度E中减去该离子本身所产生 的场强,称为有效场强,用E有效表示
N N W u W u V V
N * N E q u /1 u W / 把 E 有 效 V 3 V 0 0 3
N V
代入
u u q E 得：
* 有 效
N N N N * * W / W / qE u / 1 q V V V V 0 0 3 3 整理得： * 2 * ( ) /3 0V N q Nq W W E N V N 1 1 3 0V 3 V 0
一、长声学波 由前面一维双原子链的色散关系,声学波：
1 2 m M m M 2 1 4 2 2 () q 1 1 s i n a A q 2 m M m M ) 2 (
当波矢q
2 A qa (m M ) 2
* 有 效
其中b12 =b21, 这组方程是黄昆在1951年讨论 光学波的长波近似时引进的,通称为黄昆方程.

固体物理课件第四章：能带理论能带理论(1)

固体物理课件第四章：能带理论能带理论(1)
填充的部分（允带）和禁止填充的部分（禁带）相间组成 的能带，所以这种理论称为能带论。
需要指出的是：
在固体物理中，能带论是从周期性势场中推导出来的，这 是由于人们对固体性质的研究首先是从晶态固体开始的。而周 期性势场的引入也使问题得以简化，从而使理论研究工作容易 进行。所以，晶态固体一直是固体物理的主要研究对象。然而，
周期性势场并不是电子具有能带结构的必要条件，现已证实，
在非晶固体中，电子同样有能带结构。 电子能带的形成是由于当原子与原子结合成固体时，原子 之间存在相互作用的结果，而并不取决于原子聚集在一起是晶 态还是非晶态，即原子的排列是否具有平移对称性并不是形成 能带的必要条件。
虽然晶体中电子的运动可以简化成求解周期场作用下 的单电子薛定谔方程，但具体求解仍是困难的，而且不同 晶体中的周期势场形式和强弱也是不同的，需要针对具体 问题才能进行求解。
Hale Waihona Puke T T f r TT－ T T = 0，
晶体中单电子运动的哈密顿量应具有晶格周期性：
2 2 T Hf r T r U r f r 2m 2 2 r a U r a f r a 2m
这里b1，b2和b3为倒格子基矢，于是有
e
ika
a b 2
r R r 1a1 2a2 3a3
1 2 3 1 2 3
T T T r r
1 2 1 2 3 3
Bloch首先讨论了在晶体周期场中运动的单电子波函数
应具有的形式，给出了周期场中单电子状态的一般特征，
这对于理解晶体中的电子，求解具体问题有着指导意义。
When I started to think about it, I felt that the main problem was to explain how the electrons could sneak by all the ions in a metal, … By straight Fourier analysis I found to my delight that the wave differed from the plane wave of free electrons only by a periodic modulation.

固体物理第四章_晶体的缺陷

固体物理第四章_晶体的缺陷
刃位错
A
未滑动的晶面
EC
F
B
滑动前的晶格
D
刃位错的晶格
刃位错： F原子链。 EF是晶体的挤压区与未挤压区的分界线：
F以下原子间距变大，原子间有较强吸引力；
F的左右晶格被挤压，原子间的排斥力增大。
16
例：实际晶体的小角倾斜 晶体由倾斜角很小的两部分晶体结合而成。为了使 结合部的原子尽可能地规则排列，就得每隔一定距 离多生长出一层原子面，这些多生长出来的半截原 子面的顶端原子链就是刃错位。
添加Fe、Co、Mn等“硬性”添加物后，这些 原子占据Zr或Ti的格点，显著提高该铁电材料的 机械品质因数。
9
4、色心 能吸收光的点缺陷
完善的卤化碱晶体是无色透明的。众多的 色心缺陷能使晶体呈现一定的颜色。
例如：F心，把卤化碱晶体在相应的碱金 属蒸气中加热，然后骤冷到室温，则原来透明 的晶体就出现了颜色。
实验临界切应力比理 论值小的根源
30
2、螺位错的滑移 螺位错的滑移与刃位错的滑移相类似，只是螺位的 滑移方向与晶体所受切应力的方向相垂直。
BC原子 受到向 下的拉 力
螺位 错线 滑移
BC列原子受到右边原子的下拉力，BC原子有向下 位移的趋势，BC原子下移一定的距离； 使BC 变为螺错位。
31
二、螺位错与晶体生长
4
§4.1 晶体缺陷的基本类型
本章主要讨论单晶的缺陷：多晶体是由许多小晶粒 构成，每个晶粒可看成是小单晶。晶粒间界不仅原 子排列混乱，而且是杂质聚集的地方。因此晶粒间 界是一种性质复杂的晶体缺陷。
一、点缺陷
晶体中的填隙原子、空位、俘获电子的空位、杂质 原子等。这些缺陷约占一个原子尺寸，引起晶格周 期性在一到几个原胞范围内发生紊乱。

固体物理 第四章(1)Bloch定理

固体物理 第四章(1)Bloch定理



i

ˆ H i i r i Ei i r i


（4-9）
所有电子都满足薛定谔方程，可略去下标。只要解得 i r i , Ei ，便可得
到晶体电子体系的电子状态和能量，使一个多电子体系的问题简化成一 个单电子问题，所以上述近似也称为单电子近似。

周期势场假设
而并不考虑其它电子的具体运动情况
单电子近似并非所研究的系统只有一个电子。系统可以有多个 电子，但是波函数十单电子的波函数，多个单电子方程。但所 有单电子都满足同样的方程，因此这个单电子方程的解对所有 电子都适用，是所有电子的解。 如果该近似用到不满足这个近似的体系——强关联体系，会出 现反常现象。
4.2 能带理论的基本假设
假设在体积V=L3中有N个带正电荷Ze的离子实，相应地有NZ个价电 子，那么该系统的哈密顿量为：
2 2 1 / e2 ˆ H i 2 i , j 4 0 r i r j i 1 2m
NZ NZ N 2 2 1 ( Ne) 2 Ze 2 / n 2 i , j 4 0 R n R m i 1 n 1 4 0 r i R n i 1 2 M ˆ ˆ Te U ee r i r j Tn U nm R n R m U en r i R n N

（4-12）
的本征函数是按布拉菲格子周期性调幅的平面波，即
k
且


ik r r e uk r

（4-13）
在周期势场中运动的单电子的波函数不再 是平面波，而是调幅平面波，其振幅不再
uk r R n uk r
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章总结成员及分工1：一维晶格以及三维晶格的振动2：晶格热容的量子理论3：简谐近似和简谐坐标4：晶格的状态方程和热膨胀5：离子晶体的长波近似4－1 一维晶格以及三维晶格的振动一、知识脉络二、重点1.格波的概念和“格波”解的物理意义(1)定义：晶格原子在平衡位置附近作振动时，将以前进波的形式在晶体中传播，这种波称为格波。

(2)物理意义：一个格波解表示所有原子同时做频率为ω的振动，不同原子之间有位相差。

相邻原子之间的位相差为aq 。

(3) q 的取值范围：－(π/a)<q ≤(π／a)这个范围以外的值，不能提供其它不同的波。

q 的取值及范围常称为布里渊区（Brillouin zones ）。

(4) Born-Von Karman 边界条件: 1)(=-Naq i e h Naq ⨯=π22.一维单原子链的色散关系22241[1cos ]sin ()2aq aq m m ββω=-=把 ω 与q 之间的关系称为色散关系(disperse relation)，也称为振动频谱或振动谱。

3.一维单原子链的运动方程相邻原子之间的相互作用βδδ-≈-=d dvF ad v d ⎪⎪⎭⎫ ⎝⎛=22δβ 第n 个原子的运动方程11()(2)n n n n i t naq nq m Ae ωμβμμμμ∙∙+--=+-=4.一维双原子链中两种原子的运动方程及其解（1）运动方程( equation))2(2221212n n n n M μμμβμ---=+++∙∙ )2(2221212n n n n M μμμβμ---=+++∙∙（2）方程的解(solution)])2([2q na t i n Ae -=ωμ ])12([12aq n t i n Be +-+=ωμ5.声学波与光学波的概念与物理意义（1）声学波与光学波的定义}]sin )(41[1{2/1222aq M m mM mM M m +-++=+βω }]sin )(41[1{2/1222aq M m mMmM M m +--+=-βω ω＋对应的格波称为光学波（optic wave ）或光学支（optic branch) ；ω－对应的格波称为声学波(acoustic wave)或声学支（acoustic branch ）（2）两种格波的振幅比aq m A B cos 222ββω--=⎪⎭⎫⎝⎛++aq m A B cos 222ββω--=⎪⎭⎫⎝⎛--（3）ω＋ 与ω－ 都是q 的周期函数)()(q aq --=+ωπω)()(q aq ++=+ωπω其中aq a22ππ≤〈-6.对色散关系的讨论（1）一维单原子链与一维双原子链的格波解的差异一维单原子链只有一支格波（一个波矢对应一个格波）— 声学波；而一维双原子链则有两支格波（一个波矢对应两个格波）— 声学波和光学波，两支格波的频率各有一定的范围：0)0()(min ==--ωω Maβπωω2)2()(max ==-- m aβπωω2)2()(min ==++ mMM m )(2)0()(max +==++βωω 在ω-max 与ω+min 之间有一频率间隙，说明这种频率的格波不能被激发。

（2）声学波的物理本质声学格波反映的是原胞的整体振动，或者说是原胞质心的振动。

（3）光学波是复式格子特有的光学格波是两种原子保持质心不动的情况下作刚性的相对振动（4）q 的取值12=Na iq e π22Nahq =7.在三维晶格中，对于一定的波矢q ，有3个声学波，（3n －3）个光学波。

8. 三维晶格中“q 空间”以及q 在其中的分布密度 （1）q 空间“q 空间”亦称为波矢空间(wave vector space)。

（2）q 在波矢空间的密度分布密度 ＝V ／（2π）3（3）波矢数和格波数晶格振动的波矢数＝晶体原胞数晶格振动频率的数目＝晶格的自由度数 9.三维晶格振动谱的物理意义（1）对于原胞只含有一个原子的晶格，与一维单原子链类似，只有声学支。

不同之处在于一维单原子链的一个原子只有一个自由度，相应于一个声学支,现在除了纵波外，还可有两个原子振动方向与波传播方向垂直的横声学波存在。

（2）对于原胞包含两个以上原子的复式晶格，类似于双原子链，除声学支外还有光学支，在q ＝0 处有非零的振动频率ω。

三、难点1． 一维单原子链中原子的运动方程及其解 2． 一维单原子链的色散关系3． 一维双原子链中两种原子的运动方程及其解 4． 一维双原子链的色散关系5． 三维晶格中“q 空间”以及q 在其中的分布密度 四、基本要求1． 掌握一维单原子链振动的格波解及色散关系的求解过程，以及格波解的物理意义。

2． 掌握一维双原子链振动的色散关系的求解过程，清楚声学波与光学波的定义以及他们的物理意义 3． 了解三维晶格的振动4． 掌握q 空间意义及相关性质 五．思考题从一维双原子链色散关系出发，推导一维单原子链色散关系：当M ＝m 时，变为单原子链在考虑到双原子链，原子位置的周期性排列之后得:4-2 简正坐标主要内容：一、简谐近似的定义二、简正坐标的引入与振动模的定义 三、晶格振动和声子重点：简谐近似和简正坐标 难点：关于声子的本质的理解一、简谐近似的定义将N 个原子体系的势能函数在平衡位置附近展开成泰勒级数,忽略二阶以上的高阶项，则得到ji ji N j i V V μμμμ0231,)(21∂∂∂=∑=体系的势能函数只保留至μi 的二次方程，称为简谐近似（harmonic approximation ）。

要考虑到高阶作用的则称为非谐作用（an-harmonic interaction ）。

注：晶格振动是一个小振动问题。

对于此类问题常采用简谐近似。

上式假设平衡位置V0=0.12222411sin ()m M mM aq mM m M ωβ⎧⎫⎡⎤+⎪⎪=±-⎨⎬⎢⎥+⎣⎦⎪⎪⎩⎭12222222411sin (2)M M aq M M ωβ⎧⎫⎡⎤⎪⎪=±-⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭1222211sin aq M ωβ⎧⎫⎡⎤=±-⎨⎬⎣⎦⎩⎭{}221cos aq M βω=±{}221cos aq Mβω=-二、简正坐标的引入与振动模的定义为了使问题简化，引入简正坐标 Q1，Q2,…，Q3N ，它与位移坐标μi 之间通过如下的正交变换形式相联系jijNj i i Qa m ∑==31μ一般地说，一个简正振动并不是表示某一个原子的振动，而是表示整个晶体所有原子都参与的振动，而且它们的振动频率都相同。

由简正坐标所代表的，体系中所有原子一起参与的共同振动，常称为一个振动模或简正模（normal mode ）。

对一个体系来说，只要能找到简正坐标，或是说振动模，则体系的能量以及波函数就可以求解出来了。

对应关系系统的势能函数 系统的动能函数 系统的哈密顿量ji ji N j i V V μμμμ0231,)(21∂∂∂=∑=三、晶格振动和声子晶格振动等价于3N 个独立谐振子的振动,因此,晶格振动是这些谐振子能量的总和ii Ni n E ω )21(31+=∑=这说明,晶格振动的能量是量子化的,能量的是以ω 为单元变化的.将晶格振动的能量量子称为为声子(phonon )。

声子不是真实的粒子，称为“准粒子”(quasi-particle )，它反映的是晶格原子集体运动状态的激发单元。

虽然声子是假想的粒子,但理论和实验都已证明,其他粒子与晶格相互作用时,恰似它们与能量为ω ,动量为q 的粒子作用一样,称q 为声子的准动量.但声子不携带真实的动量. （1）声子不携带真实的动量。

（2）声子的等价性。

（3）决定晶格振动能高低的因素:晶体温度的高低是晶格振动能高低的反映。

（4）温度一定时的平均声子数23121ii N i m T ∙=∑=μH=V+T 23121iN i Q T ∙=∑=223121i i Ni Q V ω∑==)(2122231i i i N i Q p H ω+=∑=（9在高温时,平均声子数与温度成正比,与频率成反比.温度一定时,频率低的格波的声子数比频率高的格波的声子数要多.［声子－声子的相互作用］（1）非谐作用使晶格振动达到热平衡非谐作用是晶格振动达到热平衡的最主要的原因。

（2）N 过程和U 过程4－5 离子晶体的长波近似主要内容： 一、长光学波的宏观运动方程二、长光学波的横波频率ωTO 与纵波频率ωLO （LST 关系） 三、离子晶体的光学性质 四、极化激元的概念重点： 一 、长光学波的宏观运动方程及系数的推导二 、LST 关系及两个结论一、长光学波的宏观运动方程离子晶体在做长光学波振动时，由于原胞内正负离子作相对运动，因而产生宏观极化（出现宏观电偶极矩），从而可以和电磁波发生强烈相互作用。

所以长光学波与离子晶体的电学、光学性质密切相关。

对于长声学波：可以看作连续介质弹性波，它满足在弹性理论基础上建立的宏观运动方程，因此由宏观弹性介质理论即可得到长声学格波解。

对于长光学波：也可以在宏观理论的基础上进行近似处理，这就是我国著名的物理学家黄昆于1951年提出的方法。

黄昆建立了一对方程，称为黄昆方程：1112W b W b E ∙∙=+（1）2122P b W b E =+（2）这里 P 是宏观极化强度，E是宏观电场强度。

其中，方程（1）是决定离321q q q ωωω =+n G q q q +=+321子相对振动的动力学方程，称为振动方程。

方程（2）表示除去正负离子相对位移产生极化，还要考虑宏观电场存在时的附加极化，称为极化方程。

可证明b12＝b21。

系数的确定分为两种情况:1，静电场情况下，晶体的介电极化令（1）式中的0W ∙∙= 得 代入方程（2）中得（3） 因为（4）其中ε0为真空中的介电常数，ε（0）为静电介电常数 对比（3）式和（4）式知：（5）2，高频电场情况下的介电极化由W ＝0 带入（3）可得22P b E =（6）又因为 可得由上面可知且对于长光学振动，有211ω=-bω0是横光学波的频率，可以从晶体的红外吸收谱测量中得到.由上面的讨论，我们得到二、长光学波的横波频率ωTO 与纵波频率ωLO （LST 关系）1，横波和纵波满足的方程1211b W E b =-21212222211()b P b W b E b Eb =+=- 0[(0)1]P E εε=-00(0)D E P E εεε=+= 11212220]1)0([b bb -=-εε0[()1]P E εε=∞-220]1)([b =-∞εε112120)]()0([b b -=∞-εεε2011ω-=b 022]1)([εε-∞=b 02/102/12112)]()0([ωεεε∞-==b b横波满足的方程：2112TT d Wb W dt=纵波满足的方程：2212112022LL d W bb W dt bε⎛⎫=-⎪+⎝⎭2、横波与纵波的频率比（LST关系）横波与纵波的频率比2/1)()0(⎥⎦⎤⎢⎣⎡∞=εεωωTOLO这被称作为LST（Lyddano-Sachs-Teller）关系。