映射的概念教案(高一数学)MnPnUq

映射与函数教案范文第一章：映射的概念与性质1.1 映射的定义教学目标：让学生理解映射的概念，掌握映射的表示方法。

教学内容：介绍映射的定义，举例说明映射的概念。

教学方法：通过具体例子引导学生理解映射的概念，互动提问，巩固学生对映射的理解。

教学步骤：（1）引入映射的概念，引导学生思考在日常生活中遇到的映射现象。

（2）给出映射的定义，解释映射的基本要素：集合、对应关系。

（3）通过具体例子，让学生理解映射的表示方法，如图示、表格等。

（4）引导学生总结映射的性质，如单射、满射、双射等。

1.2 映射的性质教学目标：让学生掌握映射的性质，学会判断映射的类型。

教学内容：介绍映射的性质，包括单射、满射、双射等。

教学方法：通过实例分析，让学生理解映射的性质，互动提问，巩固学生对映射性质的掌握。

教学步骤：（1）回顾上一节的内容，引导学生思考映射的性质。

（2）讲解单射、满射、双射的定义与特点，举例说明。

（3）让学生通过实例分析，判断映射的类型。

（4）总结映射的性质，引导学生掌握判断映射类型的方法。

第二章：函数的概念与性质2.1 函数的定义教学目标：让学生理解函数的概念，掌握函数的表示方法。

教学内容：介绍函数的定义，举例说明函数的概念。

教学方法：通过具体例子引导学生理解函数的概念，互动提问，巩固学生对函数的理解。

教学步骤：（1）引入函数的概念，引导学生思考在日常生活中遇到的函数现象。

（2）给出函数的定义，解释函数的基本要素：定义域、值域、对应关系。

（3）通过具体例子，让学生理解函数的表示方法，如图示、表格等。

（4）引导学生总结函数的性质，如单调性、奇偶性等。

2.2 函数的性质教学目标：让学生掌握函数的性质，学会判断函数的类型。

教学内容：介绍函数的性质，包括单调性、奇偶性、周期性等。

教学方法：通过实例分析，让学生理解函数的性质，互动提问，巩固学生对函数性质的掌握。

教学步骤：（1）回顾上一节的内容，引导学生思考函数的性质。

（2）讲解单调性、奇偶性、周期性的定义与特点，举例说明。

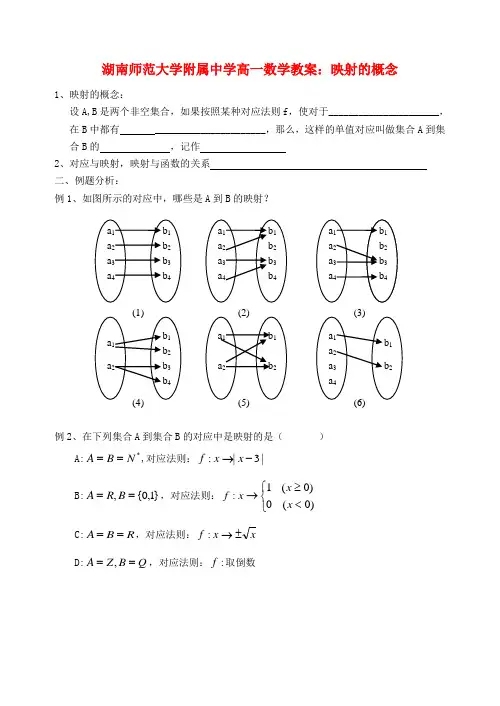
湖南师范大学附属中学高一数学教案：映射的概念1、映射的概念：设A,B 是两个非空集合，如果按照某种对应法则f ，使对于______________________，在B 中都有 ______________________，那么，这样的单值对应叫做集合A 到集合B 的 ，记作2、对应与映射，映射与函数的关系 二、例题分析：例1、如图所示的对应中，哪些是A 到B 的映射？例2、在下列集合A 到集合B 的对应中是映射的是（ ） A:*N B A ==,对应法则：|3|:-→x x f B:}1,0{,==B R A ，对应法则：⎩⎨⎧<≥→)0(0)0(1:x x x fC:R B A ==，对应法则：x x f ±→: D:Q B Z A ==,，对应法则：:f 取倒数例3、已知映射},|),{(,:R y R x y x B A B A f ∈∈==→，:f A 中的元素),(y x 对应B中的元素为)134,123(-++-y x y x（1） 求A 中元素(1,2)与B 中的哪个元素对应？ （2） A 中哪些元素与B 中元素（1,2）对应？例4、①集合{1,2,3,4},{5,6}A B ==，则A 到B 的不同映射有 个。

②集合}1,0,1{},,,{-==N c b a M ，映射NM f →:满足0)()()(=++c f b f a f ，那么映射N M f →:的个数是 个。

练习1、 若B={-1，3，5}，试找出一个集合A ，使得:21f x x →-是A 到B 的映射。

2、（全国高考题）设集合A 和B 都是自然数集N ，映射:f A B →把集合A 中的元素n 映射到集合B 的元素2nn + ，则在映射f 下，集合A 中的__________与集合B 的20对 应。

映射的概念高中教学教案一、教学目标1. 让学生理解映射的概念，掌握映射的基本性质和表示方法。

2. 培养学生运用映射的观点解决数学问题的能力。

3. 提高学生对数学概念的理解和逻辑思维能力。

二、教学内容1. 映射的定义：介绍映射的概念，解释映射的数学表达方式。

2. 映射的性质：介绍映射的单射、满射和双射的概念，解释它们的数学表达方式。

3. 映射的表示方法：介绍图示法和函数表示法，讲解它们的区别和应用。

三、教学重点与难点1. 重点：映射的概念、性质和表示方法。

2. 难点：映射性质的证明和应用。

四、教学方法1. 采用问题驱动的教学方法，引导学生通过观察、思考、探究来理解映射的概念。

2. 利用实例讲解映射的性质和表示方法，让学生在实践中掌握知识。

3. 鼓励学生进行小组讨论和交流，提高合作能力和逻辑思维能力。

五、教学过程1. 引入：通过一个实际问题，引导学生思考如何将一个集合的元素映射到另一个集合。

2. 讲解映射的定义：解释映射的概念，让学生理解映射的数学表达方式。

3. 讲解映射的性质：介绍单射、满射和双射的概念，解释它们的数学表达方式。

4. 实例分析：利用实例讲解映射的性质和表示方法，让学生在实践中掌握知识。

5. 练习与讨论：布置一些练习题，让学生巩固所学知识，并进行小组讨论和交流。

6. 总结与反思：对本节课的内容进行总结，让学生反思自己在学习过程中的收获和不足。

六、教学评价1. 评价目标：通过作业、测验和课堂表现等方式，评价学生对映射概念的理解、性质的掌握和表示方法的运用。

2. 评价方法：a) 作业：布置相关的习题，评估学生对映射概念和性质的掌握。

b) 测验：设计选择题、填空题和解答题，测试学生对映射知识的理解和应用能力。

c) 课堂表现：观察学生在讨论、提问和解答问题时的表现，评价其参与度和理解程度。

3. 评价标准：a) 映射概念理解：能够准确描述映射的定义，区分不同类型的映射。

b) 性质掌握：能够判断给定的映射是否具有单射、满射或双射性质，并给出理由。

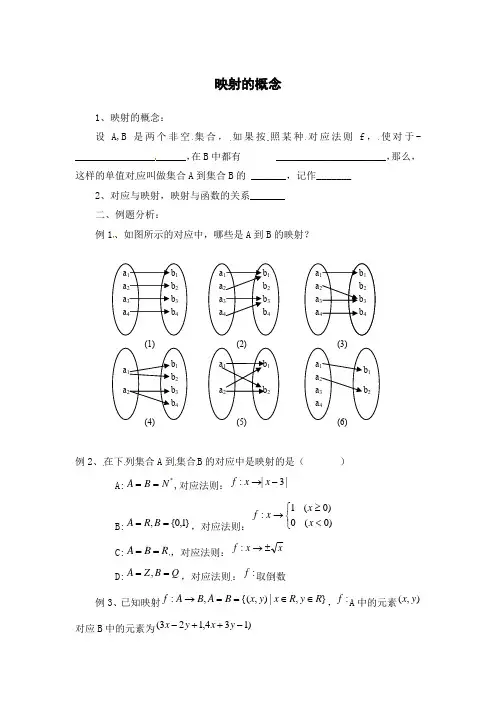
映射的概念1、映射的概念：设A,B 是两个非空集合，如果按照某种对应法则f ，使对于-______________________，在B 中都有 ______________________，那么，这样的单值对应叫做集合A 到集合B 的 _______，记作_______2、对应与映射，映射与函数的关系_______ 二、例题分析：例1、如图所示的对应中，哪些是A 到B 的映射？例2、在下列集合A 到集合B 的对应中是映射的是（ ）A:*N B A ==,对应法则：|3|:-→x x fB:}1,0{,==B R A ，对应法则：⎩⎨⎧<≥→)0(0)0(1:x x x f C:R B A ==，对应法则：x x f ±→: D:Q B Z A ==,，对应法则：:f 取倒数例3、已知映射},|),{(,:R y R x y x B A B A f ∈∈==→，:f A 中的元素),(y x 对应B 中的元素为)134,123(-++-y x y xa 1a 2 a 3 a 4b 1 b 2 b 3 b 4 a 1 a 2 a 3 a 4 b 1 b 2 b 3 b 4 a 2 a 1 a 3 a 4 b 1 b 2 b 3 b 4a 2a 1b 1 b 2 b 3 b 4 a 2a 1b 1 b 2a 2 a 1 a 3 a 4b 1 b 2(1) (2)(3)(4)(5) (6)求A 中元素(1,2)与B 中的哪个元素对应？ A 中哪些元素与B 中元素（1,2）对应？例4、①集合{1,2,3,4},{5,6}A B ==，则A 到B 的不同映射有_______个。

②集合}1,0,1{},,,{-==N c b a M ，映射NM f →:满足0)()()(=++c f b f a f ，那么映射N M f →:的个数是_______个。

练习若B={-1，3，5}，试找出一个集合A ，使得:21f x x →-是A 到B 的映射。

05 教学方法与手段
讲解与演示相结合
引入映射概念
通过生活中的实例或已学过的数学知识，引出映射的概念，帮助 学生理解其背景和意义。
定义与性质讲解
详细讲解映射的定义、性质及相关术语，如域、陪域、像、原像 等，辅以图形或动画演示，加深学生理解。
举例说明
列举不同类型的映射例子，如函数、变换等，让学生感受映射的 广泛应用。
映射的概念教学设计
目录
• 引入概念 • 映射的性质 • 映射的运算 • 映射的应用 • 教学方法与手段 • 教学评价与反馈
01 引入概念
生活中的映射现象
01
02
03
镜子中的倒影
当我们站在镜子前，镜子 中的倒影和我们的动作保 持一致，形成了一种一一 对应的关系。
电影放映
电影放映机将影片上的图 像投射到屏幕上，形成了 一种图像到图像的映射关 系。
04 映射的应用
在数学中的应用
1 2
函数
映射是数学中函数的基础概念，通过映射可以定 义函数的输入和输出关系，进而研究函数的性质 和图像。
变换
映射可以描述数学中的变换关系，如平移、旋转 、缩放等变换都可以通过映射来实现。
3
拓扑学
在拓扑学中，映射是研究空间形态和结构的基本 工具，如连续映射、同胚映射等都是拓扑学中的 重要概念。
地图导航
地图上的点和实际地理位 置的对应关系，也是一种 映射现象。
数学中的映射定义
集合间的对应关系
在数学中，映射是指两个集合之间的 一种对应关系，其中一个集合中的每 个元素都能在另一个集合中找到唯一 对应的元素。
映射的表示方法
映射的性质
包括单射、满射和双射等，分别对应 不同的元素对应关系和集合性质。

高中数学映射教学教案
教学目标：让学生了解映射的定义、性质和应用，并掌握相关的解题方法。

教学重点和难点：映射的定义和性质、映射的合成和逆映射、映射在几何中的应用。

教学准备：教材、课件、活动设计、练习题等。

教学流程：
一、引入（5分钟）
教师向学生介绍映射的概念，引导学生思考什么是映射，并举例说明。

二、概念理解（15分钟）
1. 讲解映射的定义和符号表示，让学生掌握映射的基本概念。

2. 讲解映射的性质，帮助学生理解映射的基本性质。

三、运用能力培养（20分钟）
1. 给学生一些简单的映射题目，让学生能够灵活运用映射的知识解题。

2. 引导学生进行映射的合成和逆映射的讨论和解题。

四、拓展应用（10分钟）
1. 讲解映射在几何中的应用，如平移、旋转等。

2. 给学生一些实例题目，帮助学生了解映射在几何中的具体应用。

五、总结（5分钟）
教师总结本节课的重点和难点，巩固学生对映射的理解，激发学生对数学的兴趣。

六、作业布置（5分钟）
布置相关的练习题，让学生复习本节课内容，并巩固所学知识。

教学反思：老师可以根据学生的学习情况调整教学内容和方法，确保学生能够有效地掌握映射的相关知识。

同时，鼓励学生多进行实际操作，加深对映射的理解和应用能力。

高中数学映射的教案教学目标：1. 理解数学映射的概念和基本性质。

2. 掌握如何判断一个给定关系是否为映射。

3. 能够在实际问题中应用映射的概念解决问题。

教学重点：1. 映射的定义和基本性质。

2. 判断一个给定关系是否为映射。

3. 应用映射解决实际问题。

教学难点：1. 理解映射和函数的区别。

2. 能够准确地判断一个关系是否为映射。

教学准备：1. 教师备好教材、教具和课件。

2. 学生预先学习相关知识。

3. 教师准备案例题目和练习题。

教学过程：一、导入（5分钟）教师引导学生回顾函数的概念，并告诉学生今天将学习数学映射的内容。

二、讲解映射的概念和基本性质（15分钟）1. 教师讲解映射的定义和基本性质，引导学生理解映射的概念。

2. 教师通过示例说明映射的性质，让学生加深对映射的理解。

三、判断关系是否为映射（15分钟）1. 教师讲解判断一个给定关系是否为映射的方法。

2. 教师通过案例指导学生如何判断一个关系是否为映射。

四、应用映射解决实际问题（10分钟）1. 教师给出一个实际问题，引导学生运用映射的概念解决问题。

2. 学生尝试独立解决问题，教师及时给予指导和反馈。

五、课堂练习（10分钟）学生完成几道与映射相关的练习题，巩固所学知识。

六、总结（5分钟）教师对本节课的重点内容进行总结，并提醒学生对映射的概念进行复习。

七、作业布置（5分钟）布置相关习题作业，督促学生加强练习。

教学反思：本节课主要是对数学映射的基本概念和性质进行讲解，通过案例和练习引导学生深入理解映射的概念。

教学中应注意引导学生掌握映射的判定方法和应用技巧，激发学生对数学的兴趣和学习的动力。

映射的概念与应用（高中加强版）教案章节：一、映射的定义与特性教学目标：1. 理解映射的概念及其数学定义。

2. 掌握映射的基本特性，包括单射、满射和双射。

教学内容：1. 映射的定义：介绍映射的概念，解释映射是如何将一个集合的元素对应到另一个集合的元素。

2. 映射的特性：讲解映射的单射性、满射性和双射性，并通过实例进行说明。

教学活动：1. 引入映射的概念，引导学生理解映射的定义和作用。

2. 通过具体例子，让学生观察和分析映射的特性，引导学生总结出映射的单射性、满射性和双射性的定义。

3. 进行小组讨论，让学生探索和比较不同映射的特性，并分享彼此的发现。

教学评估：1. 通过课堂提问，检查学生对映射的定义和特性的理解程度。

2. 布置课后作业，要求学生运用映射的概念和特性解决相关问题。

教案章节：二、线性映射与矩阵教学目标：1. 理解线性映射的概念及其与矩阵的关系。

2. 学会通过矩阵来表示线性映射，并掌握矩阵的运算规则。

教学内容：1. 线性映射的定义：介绍线性映射的概念，解释线性映射是如何将一个线性空间映射到另一个线性空间。

2. 矩阵与线性映射：讲解矩阵如何表示线性映射，解释矩阵的运算规则。

教学活动：1. 引导学生回顾线性空间的概念，为学生介绍线性映射的定义。

2. 通过具体例子，让学生观察和分析线性映射的性质，引导学生理解线性映射的特点。

3. 讲解矩阵与线性映射的关系，引导学生学会通过矩阵来表示线性映射。

4. 进行小组讨论，让学生探索和比较不同线性映射的矩阵表示，并分享彼此的发现。

教学评估：1. 通过课堂提问，检查学生对线性映射的定义和性质的理解程度。

2. 布置课后作业，要求学生运用线性映射的概念和矩阵的运算规则解决相关问题。

教案章节：三、映射的图像与性质教学目标：1. 学会绘制映射的图像，理解图像与映射性质之间的关系。

2. 掌握映射的基本性质，包括连续性、可积性和可微性等。

教学内容：1. 映射的图像：介绍如何绘制映射的图像，解释图像与映射性质之间的关系。

3.2 映射的概念课题：映射的概念教学目标：1．知识与技能了解映射的概念，掌握象、原象等概念及其简单应用。

2．过程与方法学会用集合与对应的语言来刻画函数，体会对应关系在刻画函数概念中的作用。

3．情感、态度与价值观树立数学应用的观点，培养学习良好的思维品质。

教学重点：映射的概念的形成与认识。

教学难点：映射的概念的形成与认识。

课型：新授课。

教学方法：启发讨论式教学用具：多媒体教学过程：一、创设情境同学们在参加中考的时候，每个人都有一张准考证，准考证上都会有一个考号，在考试的时候，同学们都会凭借着准卡证号去寻找自己的座位，也就是说通过准考证，考号与座位建立起了一种对应关系。

二、活动尝试1、在初中我们已学过一些对应的例子：（学生思考、讨论、回答）①对任意实数a，数轴上都有唯一的一点A与此相对应②坐标平面内任意一点A 都有唯一的有序数对(x, y)和它对应三、师生探究今天我们就要在这个基础之上，再结合我们前边所学过的集合的有关知识，来重点研究两个集合元素与元素之间的一种特殊的对应关系，我们把它称作为映射（板书课题）。

那对于什么是映射，我们称它为一种特殊的对应，那它又特殊在什么地方呢？所以大家跟我一起看下边的机组对应：设A，B分别是两个集合，为简明起见，设A，B分别是两个有限集求平方B说明：（2）（3）（4）这三个对应的共同特点是：对于左边集合A 中的任何一 个元素，在右边集合B 中都有唯一的元素和它对应。

映射：设A ，B 是两个集合，如果按照某种对应法则f ，对于集合A 中的任何一个元素，在集合B 中都有唯一的元素和它对应，这样的对应（包括集合A 、B 以及A 到B 的对应法则f ）叫做集合A 到集合B 的映射 记作：B A f →:象、原象：给定一个集合A 到集合B 的映射，且B b A a ∈∈,，如果元素a 和元素b 对应，则元素b 叫做元素a 的象，元素a 叫做元素b 的原象。

映射定义的分析：（学生思考、讨论、回答，教师整理、强调） ① 映射三要素：集合A 、集合B 、对应法则f.② 特殊的对应：A 中的任一元素都对应着B 中唯一的一个元素（任一对唯一）。

高中数学映射教案
一、教学目标：
1. 理解映射的概念和性质；
2. 掌握映射的表示方法；
3. 能够根据给定的映射找出它的定义域、值域和像；
4. 能够进行映射的复合和逆映射的求解；
二、教学重点：
1. 映射的概念和性质；
2. 映射的表示方法；
3. 映射的定义域、值域和像的确定；
4. 映射的复合和逆映射的求解；
三、教学难点：
1. 映射的复合；
2. 映射的逆映射；
四、教学过程：
1. 映射的概念和性质的介绍（10分钟）
教师简单介绍映射的定义及性质，引导学生理解映射的基本概念。

2. 映射的表示方法（15分钟）
教师通过具体例子演示映射的表示方法，解释映射的不同形式表示。

3. 映射的定义域、值域和像（20分钟）
教师讲解如何确定映射的定义域、值域和像的方法，通过实例进行讲解并进行练习。

4. 映射的复合（15分钟）
教师介绍映射的复合的概念和方法，通过例题演示如何进行映射的复合，并让学生自行练习。

5. 映射的逆映射（15分钟）
教师讲解映射的逆映射的概念和求解方法，通过实例进行演示并让学生进行练习。

6. 练习与检测（15分钟）
教师布置相关练习题让学生巩固所学知识，并进行检测。

五、教学反思：
通过本节课的教学，学生应该能够掌握映射的基本概念、性质和运算方法，能够熟练计算映射的复合和逆映射。

教师应该及时收集学生的反馈意见，对教学过程进行调整和改进。

一、教学目标1. 知识与技能：- 学生能够理解映射的概念，并能举例说明。

- 学生能够运用映射的概念解决简单的实际问题。

2. 过程与方法：- 通过观察、比较、分析等活动，培养学生抽象思维能力。

- 通过小组合作，提高学生的交流与合作能力。

3. 情感态度与价值观：- 培养学生对数学的兴趣和好奇心。

- 培养学生的逻辑思维能力和严谨的学术态度。

二、教学重难点1. 教学重点：- 映射的概念及其性质。

2. 教学难点：- 理解映射的抽象性，并能将其应用于实际问题。

三、教学过程（一）导入新课1. 展示生活中的实例，如配对、排序等，引导学生思考这些实例中是否存在映射关系。

2. 提问：如何定义映射？映射有什么特点？（二）新课讲授1. 概念引入：- 通过定义和例子，向学生介绍映射的概念。

- 强调映射的两个要素：定义域和值域，以及映射关系。

2. 性质分析：- 分析映射的几个重要性质，如单射、满射、双射等。

- 通过实例，帮助学生理解这些性质。

3. 应用举例：- 列举几个简单的映射实例，让学生分析其性质。

- 引导学生思考如何将映射应用于实际问题。

（三）课堂练习1. 完成几个关于映射的选择题和填空题，巩固所学知识。

2. 小组讨论：如何将映射应用于解决实际问题。

（四）课堂小结1. 回顾本节课所学内容，强调映射的概念和性质。

2. 鼓励学生在生活中寻找映射的例子。

四、教学评价1. 课堂表现：观察学生在课堂上的参与度、合作能力等。

2. 作业完成情况：检查学生对映射概念的理解和应用能力。

3. 课后反馈：通过问卷调查或访谈，了解学生对本节课的满意度和学习效果。

五、教学反思1. 教学过程中，注意引导学生理解映射的抽象性，避免死记硬背。

2. 通过实例和实际问题，让学生体会映射在生活中的应用价值。

3. 关注学生的学习差异，因材施教，提高教学质量。

六、教学资源1. 教学课件：包含映射的概念、性质、实例等。

2. 教学视频：展示映射在生活中的应用。

3. 课后练习题：帮助学生巩固所学知识。

映射概念教案教案标题：映射概念教案教学目标：1. 理解并能够解释映射概念。

2. 能够应用映射概念解决实际问题。

3. 发展学生的观察力和空间推理能力。

教学步骤：引入：1. 创设情境：播放一个图片幻灯片，图中展示各种映射现象，例如地图、图表、音符与乐器等。

2. 引导思考：通过提问引导学生思考，观察图片中不同的映射现象，问学生是否能够解释这些映射。

探究：1. 定义映射概念：引导学生讨论他们对映射概念的理解，然后引导他们总结归纳出映射的定义。

2. 实例分析：给学生提供一系列实际生活中的映射例子，如地图、图表、代数方程等，要求学生分析并解释这些例子中的映射关系。

3. 编制映射图：要求学生准备一张A4纸，一支铅笔和一些颜色笔，让他们将自己的手掌放在纸上，用铅笔勾画出手掌的轮廓，然后使用颜色笔标注出手指与纸上的位置对应关系，进一步加深对映射关系的理解。

拓展：1. 进一步应用：给学生提供一些实际问题，要求他们运用映射概念来解决，例如根据地图上的比例，计算实际距离等。

2. 探索更多映射：鼓励学生在日常生活中寻找更多的映射现象，并将其记录下来，与同学分享。

总结：1. 小结映射概念：帮助学生梳理和总结学过的内容，再次强调映射的定义和应用。

2. 作业扩展：布置一些关于映射的练习题作为课后作业，帮助学生巩固所学知识。

3. 辅导辅导：为那些在课堂上有困难的学生提供辅导和指导，确保每个学生都理解映射概念。

教学评估：1. 学生参与度：观察学生在课堂中的积极参与程度，包括发言、思考和讨论。

2. 映射图评估：评估学生制作的映射图，看是否能准确地标注出映射关系。

3. 应用问题评估：评估学生解决实际问题时运用映射概念的能力，包括问题分析、解决步骤和答案的准确性。

教学资源：1. 图片幻灯片展示各种映射现象的图片。

2. 实际生活中的映射例子，如地图、图表等。

3. A4纸、铅笔和颜色笔供学生制作映射图使用。

4. 练习题作为课后作业。

教学延伸：1. 应用数学中的映射概念，引导学生学习平面几何、代数、函数等知识。

数学教案－映射教案标题：映射教学目标：1. 理解映射的概念及其基本性质。

2. 能够通过示例判断一个给定的关系是否为映射。

3. 能够根据给定的映射规则，求一个给定元素的像。

教学重点：1. 学生能够理解映射的概念。

2. 学生能够通过示例判断一个给定的关系是否为映射。

3. 学生能够根据给定的映射规则，求一个给定元素的像。

教学难点：学生能够根据给定的映射规则，求一个给定元素的像。

教学过程：Step 1：引入映射的概念（5分钟）- 向学生解释映射是什么，并给出几个实际生活中的例子，如身高与体重的关系、年龄与阅读能力的关系等。

- 强调映射是一种特殊的关系，它将一个集合中的每个元素映射到另一个集合中的唯一元素。

Step 2：判断关系是否为映射（10分钟）- 给出一些示例关系，让学生判断它们是否为映射。

- 示例1：{(1, 2), (2, 3), (3, 4), (4, 5)}，学生应该能够判断这是一个映射关系。

- 示例2：{(1, 2), (2, 3), (3, 4), (4, 2)}，学生应该能够判断这不是一个映射关系。

- 让学生总结判断一个关系是否为映射的方法，如每个输入只能有一个输出。

Step 3：求元素的像（15分钟）- 引导学生思考如何根据给定的映射规则，求一个给定元素的像。

- 给出一些示例映射规则，让学生求出相应的元素的像。

- 示例1：f(x) = 2x，学生应该能够求出f(3) = 6。

- 示例2：f(x) = x^2，学生应该能够求出f(4) = 16。

- 提醒学生注意映射规则中的特殊情况，如分母不能为零等。

Step 4：练习与拓展（15分钟）- 让学生进行一些练习题，判断给定的关系是否为映射，并求出给定元素的像。

- 将学生分组，让每个小组设计一个自己的映射关系，并通过示例测试其他小组的判断和求像能力。

Step 5：总结与评价（5分钟）- 回顾本节课所学的内容，让学生总结映射的概念和基本性质。

2019-2020年高中数学《映射-概念》教案3 北师大必修1【教学目标】知识与技能1．了解映射的概念，会判断一个对应是否为映射；2．正确区分映射与函数的概念．过程与方法1．渗透特殊与一般的思想；2．类比函数概念，得出映射的概念．情感、态度、价值观1．感知函数概念是映射概念的生长点，了解知识间的相互关系，进而更好地从整体上系统的掌握知识；2．强化类比的思维方式；3．开阔视野，体验数学的抽象性，为进一步学习打下心理基础．【重点难点】重点：明确映射的概念；把握映射与函数的属种关系．难点：明确映射的概念．【教学过程】一、创设情境，引入课题问题：判断以下对应是否为集合A到集合B的函数：A={平面内周长为5的所有三角形}，B={平面内所有点}，f:三角形→三角形的外心．(幻灯片操作：注意标题“问题的提出”上有触发器)提问1：什么是函数？答：设A，B是两个非空的数集，如果按某种对应法则f，对于集合A中的每一个元素x，在集合B中都有惟一的元素y和它对应，这样的对应叫做从A到B的一个函数，通常记为y=f(x)．提问2：上述问题中哪一点不符合函数的概念？答：函数概念中对集合A，B要求是非空数集，而上述问题中A为平面内周长为5的所有三角形，B为平面内所有点，A和B都不是数集，仅这点不符合函数的概念．导语：尽管A和B不是数集，但这种一般集合之间的对应在数学中是非常有意义的，我们把这种一般集合之间的单值对应称为映射，本节就来研究一下映射的概念和性质．板书课题映射二、学生活动，建构数学提问3：你能否举出一些一般集合之间单值对应的例子？学生交流：1°对于任何一个实数，数轴上都有惟一的点与之对应；2°对于坐标平面内任何一个点，都有惟一的有序实数对与之对应；3°对于任意一个三角形，都有惟一确定的面积与之对应；4°我们班的每一位同学，都有惟一确定的学号与之对应．探究：我们班全体同学组成的集合为A，全体同学的学号组成的集合为B，那么A中的元素与B中的元素之间有什么样的对应关系呢？对于A中的每一个元素，在B中都有惟一的元素与之对应．(板书)三、数学理论，数学运用(一) 映射的概念一般地，设A、B是两个非空集合，如果按某种对应法则f，对于A中的每一个．．．元素，在B中都有惟一．．．．叫做集合A到集合B的映射．．的元素与之对应，那么，这样的单值对应（mapping），记作“f: A→B”．这个定义蕴含映射的4个特点：(1) 有序性，从A到B的映射与从B到A的映射属于不同的映射；(2) 任意性，A中任意元素都有像；(3) 惟一性，A在B中的像是惟一的；(4) 封闭性，像集是B的子集．例如图所示的对应中，哪些是A到B的映射？（动画演示）“一箭一雕”型“一箭多雕”型“众矢之的”型“引而不发”型发现“一箭一雕”型与“众矢之的”型对应在数学中是有意义的，即映射，进而得出俗：这箭怎么浪费怎么射，千万别省着！雅：“一对一”，“多对一”是映射，“一对多”不是映射；(板书)那么“多对多”是不是映射呢？看下面这道练习题．练习1．如图所示的对应是否为A到B的映射？结论：“多对多”不是映射．2．下列对应关系中，哪些是A到B的映射？函数？(教材第42页练习1)(1) A={1,4,9},B={-3,-2,-1,1,2,3}, f：x →x的平方根；(2) A=R，B=R，f：x →x的倒数；(3) A=R，B=R，f：x →x2-2；(4) A={平面内周长为5的所有三角形}，B={平面内所有点}，f：三角形→三角形的外心．(二) 映射与函数的关系在复习引入与课堂练习的基础上，比较映射与函数的概念映射：一般地，设A，B是两个非空集合，如果按某种对应法则f，对于A中的每一个元素，在B中都有惟一的元素与之对应，那么，这样的单值对应叫做集合A到集合B的映射，记作f：A→B．函数：一般地，设A，B是两个非空的数集，如果按某种对应法则f，对于集合A中的每一个元素x，在集合B中都有惟一的元素y和它对应，这样的对应叫做从A到B的一个函数，通常记为y=f(x)．板书映射函数补充题（试一试）1．若B={-1,3,5}，试找出一个集合A，使得f:x→2x-1是A到B的映射？(教材第42页练习2)2．已知映射f:A→B,A=B={(x,y)|x∈R,y∈R},A中的元素(x,y)对应B中的元素为(3x-2y+1,4x+3y-1),问：(1) B中的哪个元素与A中元素(1,2)对应？(2) A中的哪些元素与B中元素(1,2)对应？四、课堂小结，提高认识1．映射的概念；2．映射与函数的关系．【板书设计】2.1.4 映射一、问题的提出1．问题2．探究………………………………二、映射的概念(教材第41页)例………………………………三、映射与函数的关系………………………………四、试一试……………………………….。

映射的教案（高中加强版）一、映射的概念与性质1.1 映射的定义引入映射的概念，让学生理解映射是一种数学关系，将一个集合（定义域）中的每个元素对应到另一个集合（值域）中的元素。

通过图形、实例等方式展示映射的特点，强调映射的单射性（每个定义域元素唯一对应值域元素）和满射性（值域中每个元素都有定义域元素与之对应）。

1.2 映射的表示方法介绍常用的映射表示方法，如函数图、表格和函数表达式。

让学生通过实例理解不同表示方法的使用场景和特点。

1.3 映射的性质探讨映射的性质，包括传递性、对称性和一致性等。

通过实例和练习题让学生掌握映射性质的应用。

二、函数与映射的关系2.1 函数的概念引入函数的概念，让学生理解函数是一种特殊的映射，具有映射的性质，并且具有输入输出关系。

通过图形、实例等方式展示函数的特点，强调函数的单调性、连续性和可积性等概念。

2.2 函数与映射的关系解释函数是映射的一种特殊情况，即映射中的值域与函数的定义域相等。

通过实例和练习题让学生理解函数与映射的联系和区别。

2.3 函数的表示方法介绍常用的函数表示方法，如函数图、表格和函数表达式。

让学生通过实例理解不同表示方法的使用场景和特点。

三、线性映射与矩阵3.1 线性映射的概念引入线性映射的概念，让学生理解线性映射是一种特殊的映射，具有线性空间的特点。

通过图形、实例等方式展示线性映射的特点，强调线性映射的齐次性和线性性等概念。

3.2 矩阵与线性映射的关系解释矩阵是一种表示线性映射的工具，通过矩阵可以表示线性映射的运算和性质。

通过实例和练习题让学生理解矩阵与线性映射的联系和作用。

3.3 矩阵的运算介绍矩阵的基本运算，包括加法、减法、乘法和转置等。

让学生通过实例掌握矩阵运算的规则和性质。

四、逆映射与同态映射4.1 逆映射的概念引入逆映射的概念，让学生理解逆映射是原映射的逆运算，可以将原映射的输出映射回输入。

通过实例和练习题让学生掌握逆映射的性质和应用。

4.2 同态映射的概念引入同态映射的概念，让学生理解同态映射是一种特殊的映射，具有保持结构不变的特点。

高一数学教案：映射的概念
【摘要】欢迎来到高一数学教案栏目，教案逻辑思路清晰，符合认识规律,培养学生自主学习习惯和能力。

因此小编在此为您编辑了此文：“高一数学教案：映射的概念”希望能为您的提供到帮助。

本文题目：高一数学教案：映射的概念
教学目标：
1.了解映射的概念,能够判定一些简单的对应是不是映射;
2.通过对映射特殊化的分析，揭示出映射与函数之间的内在联系.
教学重点：
用对应来进一步刻画函数;求基本函数的定义域和值域.
教学过程：
一、问题情境
1.复习函数的概念.。

映射数学讲解高中教案
教学目标：
1. 理解映射的概念和基本性质。

2. 掌握映射的表示方法和分类。

3. 能够应用映射的概念解决实际问题。

教学重点：
1. 映射的定义和符号表示。

2. 映射的分类和特点。

3. 映射的应用。

教学难点：
1. 理解映射和函数的关系。

2. 运用映射的知识解决实际问题。

教学准备：
1. 教材：包含映射相关知识的教材。

2. 教具：黑板、彩色粉笔、投影仪等。

3. 实例：准备一些实际例题作为练习。

教学过程：
一、导入（5分钟）
通过一个简单的例子引入映射的概念，让学生了解映射的基本概念。

二、概念讲解（15分钟）
1. 映射的定义和符号表示。

2. 映射的分类和特点。

3. 映射与函数的关系。

三、示例分析（15分钟）
结合实际例题，分析映射的应用，引导学生掌握映射的运用方法。

四、练习与讨论（15分钟）
提供若干练习题，让学生在课堂上完成并进行讨论，加深对映射的理解。

五、总结与作业布置（5分钟）
总结本节课的重点内容，布置相关作业，巩固学生对映射知识的掌握。

教学反思：
映射是数学中的重要概念，理解和掌握映射的知识对于学生的数学学习起着重要的作用。

通过本节课的教学，学生能够对映射有一个初步的了解，为后续深入学习数学打下基础。