正弦、余弦函数的奇偶性

正弦与余弦知识点总结正弦与余弦的定义在直角三角形中，如果一个锐角的对边和斜边的比值为正弦值，邻边和斜边的比值为余弦值。

假设在直角三角形ABC中，∠C为90°，AB为斜边，BC为对边，AC为邻边，那么正弦与余弦的定义如下：正弦值：sin∠A=对边/斜边=BC/AB余弦值：cos∠A=邻边/斜边=AC/AB在直角三角形中，正弦与余弦的值可以用来描述角度和三角形边长的关系。

在不同的三角形中，正弦与余弦的值并不相同，但其性质和图像是相似的。

正弦与余弦的性质1. 周期性：正弦与余弦函数都具有周期性，其周期为2π。

这意味着在一个周期内，函数值将重复出现。

在[-π, π]或[0, 2π]范围内，正弦与余弦的函数图像将呈现出周期性的特点。

2. 奇偶性：正弦函数是奇函数，余弦函数是偶函数。

奇函数具有对称中心原点，即f(-x)=-f(x)，在图像上关于原点对称。

而偶函数则具有对称中心y轴，即f(-x)=f(x)，在图像上关于y轴对称。

3. 交替性：正弦与余弦函数在图像上呈现出交替变化的特点。

在一个周期内，正弦函数的最大值为1，最小值为-1；余弦函数的最大值为1，最小值为-1。

两个函数的图像像是上下振荡的波形。

4. 相关性：正弦与余弦函数是相互关联的。

在直角三角形中，三角函数的相互关系可以由勾股定理推导出来。

sin²x + cos²x = 1是三角函数基本关系式，也称为三角恒等式。

正弦与余弦的图像正弦与余弦函数的图像是学习三角函数的重要内容之一。

它们的图像形状、周期性、奇偶性等特点对于理解三角函数的性质至关重要。

正弦函数的图像是一条连续的波纹状曲线，具有周期性、奇函数特点。

其图像在[-π, π]或[0, 2π]范围内呈现出从最小值-1到最大值1的振荡变化。

正弦函数的图像具有对称性，关于原点对称。

余弦函数的图像也是一条连续的波纹状曲线，具有周期性、偶函数特点。

其图像在[-π, π]或[0, 2π]范围内同样呈现出从最大值1到最小值-1的振荡变化。

三角函数中的正弦函数与余弦函数在数学中，三角函数是研究角的性质和变化规律的重要工具。

其中，正弦函数（sine function）和余弦函数（cosine function）是最基本和常见的两个三角函数。

它们在数学、物理、工程等领域中都有广泛的应用。

本文将对正弦函数和余弦函数进行详细介绍，探讨它们的定义、性质和应用。

一、正弦函数正弦函数是三角函数中最基本的函数之一，通常用符号sin表示。

它可以通过单位圆上的点的纵坐标来定义。

在单位圆上，以圆心为原点，半径为1的圆为基准，对于圆上的任意一点P，其纵坐标y就是正弦函数的值。

正弦函数的定义域是实数集，值域是闭区间[-1,1]。

正弦函数具有以下几个重要的性质：1. 周期性：正弦函数是周期函数，其最小正周期为2π。

也就是说，对于任意实数x，有sin(x+2π)=sin(x)。

2. 奇偶性：正弦函数是奇函数，即满足sin(-x)=-sin(x)。

这意味着正弦函数关于原点对称。

3. 对称性：正弦函数具有轴对称性，即sin(π-x)=sin(x)。

4. 最值：正弦函数的最大值为1，最小值为-1。

正弦函数在数学和物理中有广泛的应用。

例如，在几何学中，正弦函数可以用来求解三角形的边长和角度。

在物理学中，正弦函数可以用来描述波动、振动等现象。

二、余弦函数余弦函数是另一个常见的三角函数，通常用符号cos表示。

它也可以通过单位圆上的点的横坐标来定义。

在单位圆上，以圆心为原点，半径为1的圆为基准，对于圆上的任意一点P，其横坐标x就是余弦函数的值。

余弦函数的定义域是实数集，值域是闭区间[-1,1]。

余弦函数具有以下几个重要的性质：1. 周期性：余弦函数也是周期函数，其最小正周期为2π。

也就是说，对于任意实数x，有cos(x+2π)=cos(x)。

2. 偶性：余弦函数是偶函数，即满足cos(-x)=cos(x)。

这意味着余弦函数关于y轴对称。

3. 对称性：余弦函数具有轴对称性，即cos(π-x)=-cos(x)。

三角函数的图像与性质三角函数是数学中的重要概念，它们的图像和性质对于初中数学学习者来说是必须掌握的内容。

在本文中，我将详细介绍三角函数的图像与性质，并给出一些例子和说明，帮助中学生和他们的父母更好地理解和应用这些知识。

一、正弦函数的图像与性质正弦函数是最基本的三角函数之一，它的图像是一条连续的曲线，呈现出周期性变化。

正弦函数的性质包括：1. 周期性：正弦函数的周期是2π，即在每个2π的区间内，正弦函数的图像重复出现。

2. 幅度：正弦函数的幅度表示波峰和波谷的最大差值，通常记为A。

幅度越大，波峰和波谷的差值越大。

3. 对称性：正弦函数的图像关于y轴对称，即f(x) = -f(-x)。

4. 奇偶性：正弦函数是奇函数，即f(x) = -f(x)。

举例说明：假设有一条正弦函数的图像，周期为2π，幅度为1。

在区间[0, 2π]内，正弦函数的图像先从0逐渐上升到1，然后下降到0，再下降到-1，最后又上升到0。

这样的周期性变化会一直重复下去。

根据正弦函数的性质，可以得出该图像关于y轴对称，且是奇函数。

二、余弦函数的图像与性质余弦函数也是一种常见的三角函数，它的图像和正弦函数有些相似，但也有一些不同之处。

余弦函数的性质包括：1. 周期性：余弦函数的周期也是2π，与正弦函数相同。

2. 幅度：余弦函数的幅度也表示波峰和波谷的最大差值，通常记为A。

与正弦函数不同的是，余弦函数的幅度表示波峰和波谷的绝对值最大差值。

3. 对称性：余弦函数的图像关于y轴对称，即f(x) = f(-x)。

4. 奇偶性：余弦函数是偶函数，即f(x) = f(x)。

举例说明：假设有一条余弦函数的图像，周期为2π，幅度为1。

在区间[0, 2π]内，余弦函数的图像先从1逐渐下降到0，然后下降到-1，再上升到0，最后又上升到1。

这样的周期性变化会一直重复下去。

根据余弦函数的性质，可以得出该图像关于y轴对称，且是偶函数。

三、正切函数的图像与性质正切函数是三角函数中的另一种重要函数，它的图像与正弦函数和余弦函数有很大的不同。

函数奇偶性的判断方法在数学中，我们经常会遇到需要判断一个函数的奇偶性的情况。

函数的奇偶性对于我们研究函数的性质和图像至关重要。

因此，掌握函数奇偶性的判断方法对于数学学习非常重要。

接下来，我将介绍一些常见的函数奇偶性的判断方法，希望能够帮助大家更好地理解和掌握这一知识点。

首先，我们来看一下奇函数和偶函数的定义。

一个函数f(x)被称为奇函数，如果对于任意的x，都有f(-x) = -f(x)成立；一个函数f(x)被称为偶函数，如果对于任意的x，都有f(-x) = f(x)成立。

简单来说，奇函数具有对称中心在原点的对称性，而偶函数则具有关于y轴的对称性。

接下来，我们来介绍一些常见函数奇偶性的判断方法。

首先是多项式函数。

对于多项式函数来说，我们可以通过观察其幂次来判断函数的奇偶性。

如果一个多项式函数中只包含偶次幂的项，那么这个函数就是偶函数；如果一个多项式函数中只包含奇次幂的项，那么这个函数就是奇函数。

如果一个多项式函数中同时包含奇次幂和偶次幂的项，那么这个函数既不是奇函数也不是偶函数。

其次是三角函数。

对于三角函数来说，我们可以通过观察其周期性来判断函数的奇偶性。

正弦函数和余弦函数是最常见的两种三角函数，它们分别是奇函数和偶函数。

正弦函数具有奇函数的性质，而余弦函数具有偶函数的性质。

另外，我们还可以通过函数图像的对称性来判断函数的奇偶性。

对于一个函数的图像来说，如果函数图像关于y轴对称，那么这个函数就是偶函数；如果函数图像关于原点对称，那么这个函数就是奇函数。

最后，我们还可以通过函数的导数来判断函数的奇偶性。

一个函数f(x)是奇函数，当且仅当它的导数f'(x)是偶函数；一个函数f(x)是偶函数，当且仅当它的导数f'(x)是奇函数。

总结一下，判断函数的奇偶性是数学中一个重要的知识点，我们可以通过观察函数的幂次、周期性、图像的对称性以及导数来判断函数的奇偶性。

掌握这些方法可以帮助我们更好地理解和分析函数的性质，为我们的数学学习打下坚实的基础。

正弦、余弦函数的性质（奇偶性、单调性）教学目的：知识目标：理解三角函数的奇、偶性和单调性；能力目标：掌握正、余弦函数的奇、偶性，并能根据正、余弦函数的单调性解题德育目标：激发学生学习数学的兴趣和积极性，培养学生勇于探究创新的精神。

教学重点：正、余弦函数的奇、偶性和单调性；教学难点：正、余弦函数奇、偶性和单调性的理解与应用教学过程：一、复习引入：(学生小组选派学生回答)定义域、值域、周期性？偶函数、奇函数的定义？ 图像有什么特征呢？设计意图：回顾三角函数的周期性，为引入三角函数的其他性质做准备。

二、讲解新课：1． 奇偶性观察正弦曲线和余弦曲线，你还能发现它们具有什么好的性质？如图象的对称性，你能证明吗？设计意图：让学生从直观发现对称，进而反映到代数性质上，发现正弦函数，余弦函数的奇偶性，使学生能从“形”与“数”两个方面来理解它们的奇偶性。

师生活动：师生——引导学生观察，不难发现各种对称性，进一步引导学生思考，这些对称性反映了函数什么特征？（奇偶性）从代数角度如何具体证明它们的奇偶性呢？共同归纳总结正弦函数，余弦函数的奇偶性：正弦函数是奇函数，余弦函数是偶函数。

考虑到学生的基础，打算先带领学生回顾函数奇偶性的概念。

(1)余弦函数的图形当自变量取一对相反数时，函数y 取同一值。

例如：f(-3π)=21,f(3π)=21 ,即f(-3π)=f(3π)；…… cos(－x)=cosx ∴f(-x)= f(x).以上情况反映在图象上就是：如果点（x,y ）是函数y=cosx 的图象上的任一点,那么,与它关于y 轴的对称点(-x,y )也在函数y=cosx 的图象上，这时，我们说函数y=cosx 是偶函数。

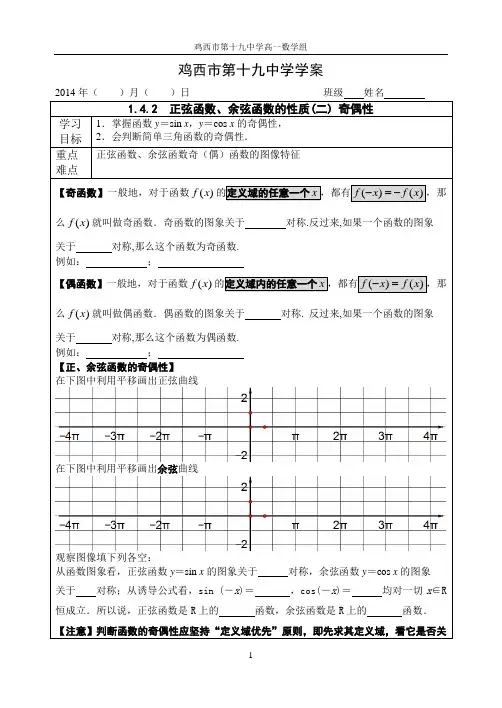
(2)正弦函数的图形观察函数y=sinx 的图象，当自变量取一对相反数时，它们对应的函数值有什么关系？ 这个事实反映在图象上，说明函数的图象有怎样的对称性呢？函数的图象关于原点对称。

也就是说，如果点（x,y ）是函数y=sinx 的图象上任一点，那么与它关于原点对称的点（-x,-y ）也在函数y=sinx 的图象上，这时，我们说函数y=sinx 是奇函数。

三角函数正弦与余弦的定义三角函数是数学中研究角与边之间关系的重要工具，其中正弦和余弦是最常见的两个三角函数。

它们既有几何意义，又有代数定义，对于描述周期性现象和解决各种实际问题都非常重要。

一、正弦函数的定义正弦函数（sine function）是一个周期函数，通常用sin(x)表示。

它的定义基于单位圆上的点的纵坐标。

我们先来回顾一下单位圆的概念。

单位圆是半径为1的圆，圆心位于原点(0,0)。

对于单位圆上的任意一点P(x,y)，点P与圆心O之间的线段OP被称为半径，而角度θ则是线段OP与正半轴之间的夹角。

正弦函数的定义是通过角度θ与单位圆上的点的纵坐标y的对应关系来确定。

具体地，对于角度θ，其对应的正弦值sin(θ)等于单位圆上点P的纵坐标y。

即：sin(θ) = y这里θ可以是任意实数，正弦函数的定义域是整个实数集，值域是[-1,1]。

二、余弦函数的定义余弦函数（cosine function）也是一个周期函数，通常用cos(x)表示。

类似于正弦函数，余弦函数的定义基于单位圆上的点的横坐标。

对于单位圆上的任意一点P(x,y)，点P与圆心O之间的线段OP被称为半径，而角度θ则是线段OP与正半轴之间的夹角。

余弦函数的定义是通过角度θ与单位圆上的点的横坐标x的对应关系来确定。

具体地，对于角度θ，其对应的余弦值cos(θ)等于单位圆上点P的横坐标x。

即：cos(θ) = x同样地，θ可以是任意实数，余弦函数的定义域也是整个实数集，值域也是[-1, 1]。

三、正弦和余弦函数的性质正弦和余弦函数具有一些重要的性质，这些性质在解决各种实际问题和进行数学计算时非常有用。

1. 周期性：正弦和余弦函数都是周期函数，周期分别为2π。

也就是说，对于任意实数x，有sin(x+2π) = sin(x)和cos(x+2π) = cos(x)成立。

2. 奇偶性：正弦和余弦函数具有不同的奇偶性。

正弦函数是奇函数，即sin(-x) = -sin(x)；而余弦函数是偶函数，即cos(-x) = cos(x)。

第二型曲线积分的奇偶性
第二型曲线积分的奇偶性是一个值得研究的流行话题，是数学家们最关注的课题。

第二型曲线积分奇偶性指的是曲线积分中正弦和余弦函数的奇偶性。

正弦和余弦函数都是奇函数，它们在0点对称，而在2π以外，它们都可以那些基本形状不变地得以翻转。

这种对称性还可以用简单的几何学方式来证明。

当把一半部分翻转并且移动到另一半时，所有的贝塞尔曲线就会完美地对齐，从而得到一个完整的曲线。

这说明正弦和余弦函数的积分是奇偶的，而其他一系列函数的积分也是如此。

第二型曲线积分的奇偶性也可以通过数学方法，特别是微分方程来推导。

假设f(x)是一个定义在[-a,a]之间的函数，它在y = 0处是双射的，且具有对称性，我们可以证明f(-x) = f(x)。

而由f(x)的积分曲线g(x)也具有同样的奇偶性。

即
g(-x) = -g(x)。

归结起来，我们可以得出结论：第二型曲线积分的奇偶性表明，正弦和余弦函数的积分是奇偶的。

第二型曲线积分的奇偶性在数学中有着广泛的应用，但这一概念也可以包含在我们的日常生活科学中。

人们经常可以在日常生活中观察到自然界中的对称性，比如夕阳沉没在地平线上时，其一半会隐没在夜幕中，另一半则亮堂如继。

这一形象就是第二型曲线积分的奇偶特性体现，无论从自然界或数学学科中，都会将我们为之震撼。

三角函数的奇偶性三角函数是数学中常见的函数类型，包括正弦函数、余弦函数和正切函数等。

在研究三角函数的性质时，一个重要的特征是它们的奇偶性。

本文将介绍三角函数的奇偶性，并分析其在不同象限内的取值范围。

1. 正弦函数的奇偶性正弦函数sin(x)的定义域是所有实数，其图像关于原点对称。

我们可以观察到，当x取负值时，sin(x)的值与当x取正值时的值相反，这说明sin(x)是奇函数。

根据正弦函数的性质，sin(x + π) = -sin(x)，可以推导出sin(x + 2π) = sin(x)，以及sin(x + 4π) = sin(x)，以及更一般的sin(x + nπ) = sin(x)。

这意味着正弦函数是以2π为周期的周期函数，并且在每个周期内保持奇偶性不变。

2. 余弦函数的奇偶性余弦函数cos(x)的定义域也是所有实数，与正弦函数类似，余弦函数关于y轴对称。

当x取负值时，cos(x)的值与当x取正值时的值相同，这说明cos(x)是偶函数。

同样地，根据余弦函数的性质，cos(x + π) = -cos(x)，可以推导出cos(x + 2π) = cos(x)，以及cos(x + 4π) = cos(x)，以及更一般的cos(x +nπ) = cos(x)。

余弦函数也是以2π为周期的周期函数，并且在每个周期内保持奇偶性不变。

3. 正切函数的奇偶性正切函数tan(x)定义于除去一切x + (2n + 1)π/2（其中n为整数）的实数上。

正切函数在定义域内既不是奇函数也不是偶函数。

我们可以发现，tan(x + π) = tan(x)，也就是说，正切函数的周期性为π。

然而，tan(x)并不保持奇偶性不变。

当x取负值时，tan(x)的值与当x取正值时的值相反，这说明正切函数既不是奇函数也不是偶函数。

4. 三角函数的取值范围在研究三角函数时，我们还需要了解它们在不同象限内的取值范围。

- 正弦函数的取值范围是[-1, 1]，在第一象限和第二象限为正，在第三象限和第四象限为负。