第二章-卷积与与卷积积分

第2章 线性时不变连续系统的时域分析2.1 学习要求（1）会建立描述系统激励与响应关系的微分方程；（2）深刻理解系统的完全响应可分解为：零输入响应与零状态响应，自由响应与强迫响应，瞬态响应与稳态响应；（3）深刻理解系统的零输入线性与零状态线性，并根据关系求解相关的响应； （4）会根据系统微分方程和初始条件求解上述几种响应； （5）深刻理解单位冲激响应的意义，并会求解；（6）深刻理解系统起始状态与初始状态的区别，会根据系统微分方程和输入判断0时刻的跳变情况； （7）理解卷积运算在信号与系统中的物理意义和运算规律，会计算信号的卷积。

； 2.2 本章重点（1）系统（电子、机械）数学模型（微分方程）的建立； （2）用时域经典法求系统的响应； （3）系统的单位冲激响应及其求解；（4）卷积的定义、性质及运算，特别是()t δ函数形式与其它信号的卷积； （5）利用零输入线性与零状态线性，求解系统的响应。

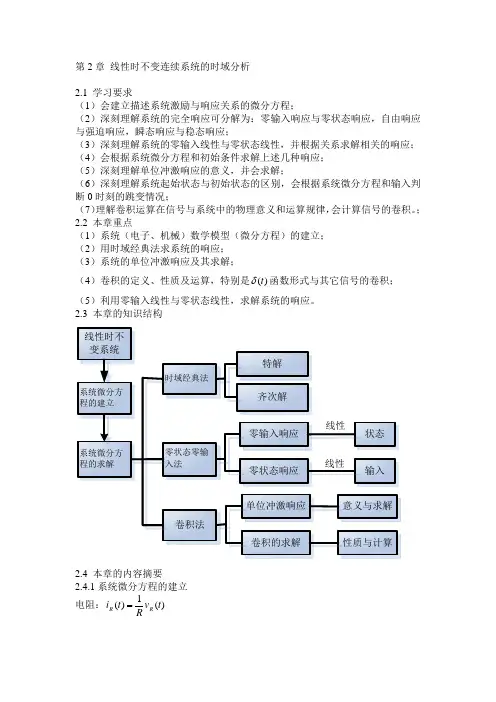
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻：)(1)(t v Rt i R R =电感：dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容：dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。

齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时，如1λ有k 重根，则响应于1λ的重根部分将有k 项，形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根，即bi a +=2,1λ，则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根，即共有m 重ib a ±=2,1λ的复根，则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。

卷积积分的定义卷积积分是数字信号处理中最常见的数学运算之一，其定义可以简单地描述为：将一个信号与另一个信号“褶积”在一起，以求出它们之间的关系或者产生的效果。

在实际应用中，卷积积分广泛用于信号处理、图像处理和通信工程等领域，是数字信号处理基础重要的处理运算。

首先，我们来看一下离散信号的卷积积分，以了解其定义和运算步骤。

假设有两个离散信号f[n]和g[n]，它们的长度依次为M和N。

那么它们的卷积积分定义为：s[n] = ∑(f[k]g[n-k])，k从0到M-1上式表示的是，将g[n]相对于f[n]做移位运算，按其对应的系数f[k]进行加权之后，再将所有元素相加，就可以得到卷积积分结果s[n]。

这个过程实际上是一种加权和计算，位于g[n]的每一个系数都和f[n]的相应系数进行乘积，然后将它们相加以得到最终的卷积积分结果。

卷积积分运算可以理解为一个滑动窗口，它在f[n]中移动，并将窗口大小限定为g[n]的长度。

随着滑动窗口移动，计算得到的结果被放置到s[n]中，这个过程一直持续到窗口完全移出f[n]。

在计算过程中，g[n]每移动一次，窗口中的每个元素将会和f[n]的相应元素进行乘积，然后将它们相加来得到s[n]中的一个元素。

需要注意的是，在卷积积分的定义中，n的取值是从0到M+N-2，这是因为卷积积分的长度为(M+N-1)。

如果n的取值超过了这个范围，那么最终的结果将会是无效和不必要的。

除了离散信号卷积积分之外，连续信号卷积积分也是数字信号处理中常见的一种运算。

其计算过程与离散信号相似，只是在信号中，连续时间变量t所涉及的积分替换掉离散时间变量n：s(t) = ∫ f(τ)g(t-τ)dτ，τ从负无穷到正无穷上式表示的是，将g(t)相对于f(t)做移位运算，按其对应的函数f(τ)进行加权之后，再将所有元素相加，就可以得到连续信号卷积积分结果s(t)。

这个过程和离散信号的卷积积分类似，只是积分替换了离散信号中的累加。

1引言信号的卷积是针对时域信号处理的一种分析方法，信号的卷积一般用于求取信号通过某系统后的响应。

在信号与系统中，我们通常求取某系统的单位冲激响应，所求得的h(k)可作为系统的时域表征。

任意系统的系统响应可用卷积的方法求得。

离散时间信号是时间上不连续的“序列”，因此，激励信号分解为脉冲序列的工作就很容易完成，对应每个样值激励，系统得到对此样值的响应。

每一响应也是一个离散时间序列，把这些序列叠加既得零状态响应。

因为离散量的叠加无需进行积分，因此，叠加过程表现为求“卷积和”。

LabVIEW是一种程序开发环境，由美国国家仪器（NI）公司研制开发的，类似于C和BASIC开发环境，但是LabVIEW与其他计算机语言的显著区别是：其他计算机语言都是采用基于文本的语言产生代码，而LabVIEW使用的是图形化编辑语言G编写程序，产生的程序是框图的形式。

本课程设计就是利用LabVIEW软件来实现方波序列卷积的过程，然后对方波序列移位过程进行演示，通过卷积过程演示和卷积和的波形图可以看出，方波序列的幅值大小不会影响卷积和的宽度而方波序列的宽度大小就会影响卷积序列相交部分的范围宽度即卷积宽度。

通过labview你能直观清晰地观察卷积的过程。

2虚拟仪器开发软件LabVIEW8.2入门2.1 LabVIEW介绍LabVIEW（Laboratory Virtual Instrument Engineering Workbench）是一种用图标代替文本行创建应用程序的图形化编程语言。

传统文本编程语言根据语句和指令的先后顺序决定程序执行顺序，LabVIEW 则采用数据流编程方式，程序框图中节点之间的数据流向决定VI及函数的执行顺序。

VI指虚拟仪器，是 LabVIEW]的程序模块。

LabVIEW 提供很多外观与传统仪器（如示波器、万用表）类似的控件，可用来方便地创建用户界面。

用户界面在 LabVIEW中被称为前面板。

使用图标和连线，可以通过编程对前面板上的对象进行控制。

离散卷积：1. 找出以下离散时间系统的脉冲响应： )[]0.2[1][][1]a y n y n x n x n +-=-- )[] 1.2[1]2[1]b y n y n x n +-=-)[]0.24([][1][2][3])c y n x n x n x n x n =+-+-+- )[][]0.5[1][2]d y n x n x n x n =+-+-2. 计算以下卷积，x[n]*v[n])[][][4],[]0.5[]n a x n u n u n v n u n =--=)[][1482],[][01234](n )b x n v n ==顺序均从=0开始)[][],[]2(0.8)[]n c x n u n v n u n == )[][1],[]2(0.5)[]n d x n u n v n u n =-=1. )[]0.2[1][][1]a y n y n x n x n +-=--[]0.2[1][][1]h n h n n n δδ+-=--1[0]0.2[1][0][1]1[1]0.2[0][1][0] 1.2[2]0.2[1][2][1]0.24[3]0.2[2][3][2]0.048[](0.2)( 1.2)n h h h h h h h h h n δδδδδδδδ-=--+--==-+-=-=-+-==-+-=-=--≥当n 1)[] 1.2[1]2[b y n y n x n +-=-[] 1.2[1]2[1]h n h n n δ+-=-21[0] 1.2[1]2[1]0[1] 1.2[0]2[0]2[2] 1.2[1]2[1] 1.2(2)[3] 1.2[2]2[2]( 1.2)(2)[]( 1.2)(2)n 1n h h h h h h h h h n δδδδ-=--+-==-+==-+=-=-+=-=-≥当时)[]0.24([][1][2][c y n x n x n x n x n =+-+-+-[]0.24([][1][2][3])0.24030h n n n n n n δδδδ=+-+-+-≤≤⎧=⎨⎩其它)[][]0.5[1][d y n x n x n x n =+-+-[][]0.5[1][2]100.51[]120h n n n n n n h n n n δδδ=+-+-=⎧⎪=⎪=⎨=⎪⎪⎩为其它值2.5450)[][][4],[]0.5[]012040.50.50.50.512n n knn n k a x n u n u n v n u n n --==--=-≤≤===-+-∑[]*[][][]([][4])0.5[]k n kk x n u n x k v n ku ku k u n k +∞=-∞+∞-=-∞=-=---∑∑如果04n ≤≤ 10120.50.5(0.52)12n nn knn k +-=-===---∑如果n>4 5450120.50.50.50.512n knn n k --=-===-+-∑)[][1482],[][01234](n )b x n v n ==顺序均从=0开始[]148200000[]0123400000123416328048122460816402[][0161934443880]x n v n y n === )[][],[]2(0.8)[]n c x n u n v n u n ==01n[]*[][]2(0.8)[]2(0.8)2(0.8)(0.8)1 1.2521 1.258[0.8 1.25],08(0.8)10,n kk nnn knkk k n n n x n v n u k u n k n n +∞-=-∞--==+=-==-=-=--≥=-+≥∑∑∑（0.8）)[][1],[]2(0.5)[]n d x n u n v n u n =-=110112[]*[][1]2(0.5)[]2(0.5)2(0.5)22(0.5)(21)122(0.5)[1]122(0.5)(22)(0.5)4,1nk nn kk nnkk nn k k n nn n n x n v n u k u n k n +∞=-∞-===++-=--===--=--=-+=-+≥∑∑∑∑连续时间卷积：1．求出以下卷积()()*()y t x t h t =，其中()()(4);()()x t u t u t h t r t =--= 2．计算以下卷积：3. 如果()sin(2)()h t t u t =，计算系统对输入()2(10)x t u t =-的响应。

卷积公式卷积的物理意义是将输入信号用时移加权的单位冲激信号和（积分）表示，然后输出就是各个冲激信号作用系统后再求和，而时移量u（f(t-u)），再对u积分，就产生了反转。

卷积的物理意义(2009-11-30 09:25:54)卷积这个东东是“信号与系统”中论述系统对输入信号的响应而提出的。

因为是对模拟信号论述的，所以常常带有繁琐的算术推倒，很简单的问题的本质常常就被一大堆公式淹没了，那么卷积究竟物理意义怎么样呢？卷积表示为y(n) = x(n)*h(n)假设0时刻系统响应为y(0),若其在1时刻时，此种响应未改变，则1时刻的响应就变成了y(0)+y(1),叫序列的累加和（与序列的和不一样）。

但常常系统中不是这样的，因为0时刻的响应不太可能在1时刻仍旧未变化，那么怎么表述这种变化呢，就通过h(t)这个响应函数与x(0)相乘来表述，表述为x(m)×h(m-n)，具体表达式不用多管，只要记着有大概这种关系，引入这个函数h(t)就能够表述y(0)在1时刻究竟削弱了多少，然后削弱后的值才是y(0)在1时刻的真实值，再通过累加和运算，才得到真实的系统响应。

再拓展点，某时刻的系统响应往往不一定是由当前时刻和前一时刻这两个响应决定的，也可能是再加上前前时刻，前前前时刻，前前前前时刻，等等，那么怎么约束这个范围呢，就是通过对h(n)这个函数在表达式中变化后的h(m-n)中的m 的范围来约束的。

即说白了，就是当前时刻的系统响应与多少个之前时刻的响应的“残留影响”有关。

当考虑这些因素后，就可以描述成一个系统响应了，而这些因素通过一个表达式（卷积）即描述出来不得不说是数学的巧妙和迷人之处了。

对于非数学系学生来说，只要懂怎么用卷积就可以了，研究什么是卷积其实意义不大,它就是一种微元相乘累加的极限形式。

卷积本身不过就是一种数学运算而已。

就跟“蝶形运算”一样，怎么证明，这是数学系的人的工作。

在信号与系统里，f(t)的零状态响应y(t)可用f(t)与其单位冲激响应h(t) 的卷积积分求解得，即y(t)=f(t)*h(t)。