信号与系统教学课件-§2.6 卷积及其性质和计算

第二章连续时间系统的时域分析§2.5冲激响应与阶跃响应§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University §2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University §2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University §2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University §2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University §2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University§2.5冲激响应与阶跃响应2天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University §2.5冲激响应与阶跃响应天津医科大学生物医学工程学院School of Biomedical Engineering, Tianjin Medical University §2.5冲激响应与阶跃响应。

信号与系统中卷积的作用大家好，今天咱们聊聊“卷积”，这个在信号与系统中很重要的概念。

别被它复杂的名字吓到了，卷积其实可以用简单的例子来解释清楚。

1. 卷积是什么1.1 卷积的简单定义首先，卷积就是一种数学运算，能够帮助我们理解一个信号在经过系统后会变成什么样。

想象一下，你有一个信号（比如一段音乐），还有一个系统（比如一个音响），卷积就是用来描述这个音响如何把音乐的每个细节都加进去的过程。

1.2 举个例子你可以把卷积想象成做菜时的调料加法。

比如，你做了一道红烧肉，肉本身的味道还不够丰富，你需要加盐、糖、生抽等调料。

每一种调料的量和种类都会影响最终的味道。

这就像卷积一样，把各种不同的“调料”混合到原始信号里，得到最终的效果。

2. 卷积在信号处理中的作用2.1 信号的滤波卷积的一个主要作用就是滤波。

说白了，就是清理信号的“杂质”。

比如你听到一首音乐，但背景有很多噪音，这时你需要一个滤波器来去掉这些噪音，让音乐变得更加清晰。

卷积在这里就像是一个聪明的清洁工，把噪音“擦干净”，留下干净的音乐。

2.2 特征提取另一个重要的作用是提取信号的特征。

想象你在看一张图片，卷积操作就像是用不同的滤镜来突出图片中的某些细节。

比如你可以用卷积滤镜来找到图片中的边缘，或者突出某些颜色的区域。

这对图像处理和计算机视觉特别重要，可以帮助我们更好地分析和理解图像。

3. 卷积的实际应用3.1 音频处理在音频处理领域，卷积有着不可替代的作用。

例如，在录音的时候，我们会用卷积来模拟不同的环境效果。

比如，你在一个大教堂里录音，卷积可以帮助你模拟教堂的回声效果，让录音听起来更有现场感。

这种效果在音乐制作和电影配乐中都很常见。

3.2 图像处理在图像处理中，卷积用于锐化、模糊等各种效果。

比如，你用照片编辑软件想让一张模糊的图片变得清晰，那就是用到了卷积技术。

你可以用它来调整图片的清晰度、对比度，甚至可以做一些酷炫的特效，让你的图片看起来更棒。

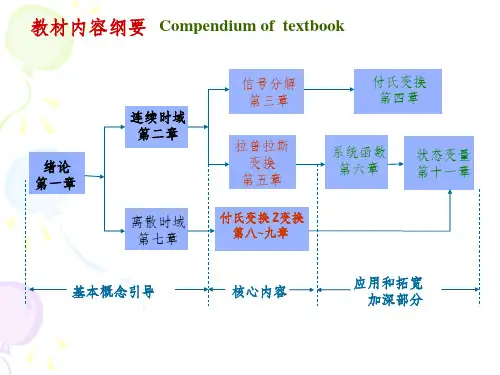
《信号与系统教案》PPT课件第一章：信号与系统导论1.1 信号的定义与分类定义：信号是自变量为时间（或空间）的函数。

分类：连续信号、离散信号、模拟信号、数字信号等。

1.2 系统的定义与分类定义：系统是一个输入与输出之间的映射关系。

分类：线性系统、非线性系统、时不变系统、时变系统等。

1.3 信号与系统的研究方法数学方法：微分方程、差分方程、矩阵分析等。

图形方法：波形图、频谱图、相位图等。

第二章：连续信号与系统2.1 连续信号的性质连续时间：自变量为连续的实数。

有限能量：能量信号的能量有限。

有限带宽：带宽有限的信号。

2.2 连续系统的特性线性特性：叠加原理、齐次性原理。

时不变特性：输入信号的延迟不会影响输出信号。

2.3 连续信号的运算叠加运算：两个连续信号的叠加仍然是连续信号。

齐次运算：连续信号的常数倍仍然是连续信号。

第三章：离散信号与系统3.1 离散信号的性质离散时间：自变量为离散的整数。

有限能量：能量信号的能量有限。

有限带宽：带宽有限的信号。

3.2 离散系统的特性线性特性：叠加原理、齐次性原理。

时不变特性：输入信号的延迟不会影响输出信号。

3.3 离散信号的运算叠加运算：两个离散信号的叠加仍然是离散信号。

齐次运算：离散信号的常数倍仍然是离散信号。

第四章：模拟信号与系统4.1 模拟信号的定义与特点定义：模拟信号是连续时间、连续幅度、连续频率的信号。

特点：连续性、模拟性、无限可再生性。

4.2 模拟系统的特性线性特性：叠加原理、齐次性原理。

时不变特性：输入信号的延迟不会影响输出信号。

4.3 模拟信号的处理方法模拟滤波器：根据频率特性对模拟信号进行滤波。

模拟调制：将信息信号与载波信号进行合成。

第五章：数字信号与系统5.1 数字信号的定义与特点定义：数字信号是离散时间、离散幅度、离散频率的信号。

特点：离散性、数字化、抗干扰性强。

5.2 数字系统的特性线性特性：叠加原理、齐次性原理。

时不变特性：输入信号的延迟不会影响输出信号。

信号系统与卷积在不少程序员眼中，卷积这个数学概念是很神秘很难懂的。

由于其在数学、物理学、电子工程、信号处理、计算机科学中极为重要，所以我试图在本文中讲解卷积的概念，力求易读易懂，让尽可能多的人理解卷积。

前几天见到VC知识库论坛上有人提问：“卷积是什么意思？”，似乎女友也问过类似问题，所以我想很有必要澄清这个既基础又重要的卷积概念。

如果您已经对此非常了解，那完全可以忽略本文了。

本文的目标读者是那些见了卷积这两个字就头大，又迫于工作需要，必须弄懂的人。

我假设您已经通过了大学一年级的高数考试，但现在已经忘得差不多了J。

很多教科书一上来就会给出卷积的定义，接着就是一串推导、证明、例子，如果你不太适应这种方式，那本文可能会非常适合你。

卷积在信号处理领域中尤为常用，就以此慢慢引入卷积概念吧。

日常生活中到处都是信号系统，它们接受一定的输入后，会给出一定的输出：手机受到对方来电的信号就会响铃或震动；电脑接到一串按键信号，屏幕就会输出一串对应的字符；女友在收到男友送的一束玫瑰后也许会送上一个热吻……现在，我们把这些信号系统抽象成“黑匣子”，不管它的内部构造，而只关注它对输入的响应。

数学化一点儿，将一个给定的信号系统记为S，设输入信号为x(t)，输出信号为y(t)，t可以代表时间，也可以是其它什么。

那么：y(t) = S{ x(t) }就表示系统S将x(t)这个输入信号转化为输出信号y(t)。

太一般化的信号系统不容易研究，那就加入一些“合理的”限制条件。

S是连续（continuous）的，如果t可以连续变化；特别的，x(t)和y(t)都是定义在实数域上的函数。

物理世界中的信号系统大多是连续的。

S是离散（discrete）的，如果t只能取一些分立的值；特别的，x(t)和y(t) 都是定义在整数域上的函数。

离散的信号系统可以比较方便的被计算机分析处理。

S是线性（linear）的，如果对任意两个输入信号x1、x2和任意的常数c1和c2有：S{ c1x1(t) + c2x2(t) } = c1S{ x1(t) } + c2S{ x2(t) }拿超市作比喻，我跟女友去买2斤萝卜和3斤白菜，即c1=2，c2=3，x1是萝卜，x2是白菜。