离散傅立叶变换及谱分析

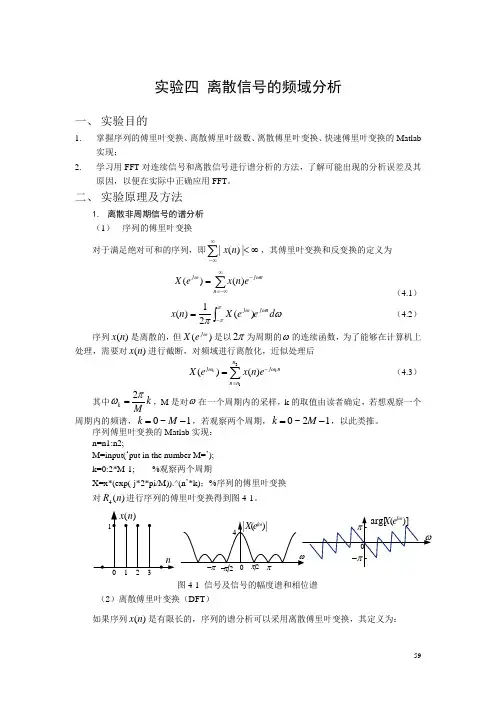
实验四 离散信号的频域分析一、 实验目的1. 掌握序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换的Matlab 实现；2.学习用FFT 对连续信号和离散信号进行谱分析的方法，了解可能出现的分析误差及其原因，以便在实际中正确应用FFT 。

二、 实验原理及方法1. 离散非周期信号的谱分析 （1） 序列的傅里叶变换对于满足绝对可和的序列，即∞<∑∞∞-|)(|n x ，其傅里叶变换和反变换的定义为∑∞-∞=-=n nj j en x e X ωω)()( （4.1）ωπωππωd eeX n x nj j ⎰-=)(21)( （4.2）序列)(n x 是离散的，但)(ωj e X 是以π2为周期的ω的连续函数，为了能够在计算机上处理，需要对)(n x 进行截断，对频域进行离散化，近似处理后21()()kk n j j nn n X ex n eωω-==∑（4.3）其中2k k Mπω=，M 是对ω在一个周期内的采样，k 的取值由读者确定，若想观察一个周期内的频谱，0~1k M =-，若观察两个周期，0~21k M =-，以此类推。

序列傅里叶变换的Matlab 实现： n=n1:n2;M=input(…put in the number M=‟); k=0:2*M-1; %观察两个周期X=x*(exp(-j*2*pi/M)).^(n ‟*k)；%序列的傅里叶变换 对4()R n 进行序列的傅里叶变换得到图4-1。

图4-1 信号及信号的幅度谱和相位谱（2）离散傅里叶变换（DFT ）如果序列)(n x 是有限长的，序列的谱分析可以采用离散傅里叶变换，其定义为：10,)()]([)(10-≤≤==∑-=N k W n x n x DFT k X N n knN（4.4）10,)(1)]([)(1-≤≤==∑-=-N n Wk X Nk X IDFT n x N k kn N（4.5）因为)(n x 与)(k X 都是离散的，所以可以利用计算机进行数值计算。

离散傅里叶变换时移-概述说明以及解释1.引言1.1 概述离散傅里叶变换（Discrete Fourier Transform，简称DFT）是一种将一个离散信号（或称时域信号）转换为频域表示的数学工具。

在现代信号处理和通信领域中，DFT被广泛应用于信号分析、滤波、频谱估计等领域。

DFT的概念源于傅里叶分析，它是将一个连续时间函数表示为一组基函数乘以一系列复数系数的线性组合。

而离散傅里叶变换则是将这一思想应用于离散信号，将离散时间序列转换为离散频率表示。

通过使用离散傅里叶变换，我们可以将一个时域上的离散信号转换为频域上的频谱表示，从而可以更加直观地观察信号的频率成分和能量分布。

离散傅里叶变换的时移性质是指当输入信号在时域上发生时移时，其在频域上的表示也随之发生相应的时移。

这一性质使得我们可以通过时移操作对信号进行处理和分析。

具体来说，如果我们对一个信号进行时移操作，即将信号中的每个样本向前或向后平移若干个位置，那么该信号在频域上的表示也会相应地发生同样的平移。

在本文中，我们将着重讨论离散傅里叶变换时移的原理和性质。

我们将介绍离散傅里叶变换的基本概念和原理，包括如何进行DFT变换、如何计算DFT系数以及DFT的逆变换等。

然后，我们将详细解释离散傅里叶变换的时移性质，包括时域上的时移操作如何在频域上体现以及时域和频域之间的变换关系等。

通过对离散傅里叶变换时移性质的研究，我们可以更好地理解信号在时域和频域之间的关系，以及对信号进行时移操作的影响。

同时，我们还将探讨离散傅里叶变换时移的应用，包括在信号处理、通信系统和图像处理等领域中的具体应用案例。

通过这些应用案例，我们将展示离散傅里叶变换时移的重要性以及它在实际问题中的实用价值。

1.2 文章结构文章结构部分的内容：本文主要分为三个部分：引言、正文和结论。

在引言部分，首先概述了离散傅里叶变换时移的主题，介绍了离散傅里叶变换的基本概念和原理。

接着，详细说明了本文的结构，即按照离散傅里叶变换时移的相关性质展开论述。

基于Matlab的DFT及FFT频谱分析基于Matlab的DFT及FFT频谱分析一、引言频谱分析是信号处理中的重要任务之一，它可以揭示信号的频率特性和能量分布。

离散傅里叶变换（DFT）及快速傅里叶变换（FFT）是常用的频谱分析工具，广泛应用于许多领域。

本文将介绍通过Matlab进行DFT及FFT频谱分析的方法和步骤，并以实例详细说明。

二、DFT及FFT原理DFT是一种将时域信号转换为频域信号的离散变换方法。

它将信号分解成若干个正弦和余弦函数的叠加，得到频率和幅度信息。

FFT是一种高效的计算DFT的算法，它利用信号的对称性和周期性，将计算复杂度从O(N^2)降低到O(NlogN)。

FFT通过将信号分解成不同长度的子序列，递归地进行计算，最终得到频谱信息。

三、Matlab中的DFT及FFT函数在Matlab中，DFT及FFT可以通过内置函数进行计算。

其中，DFT使用函数fft，FFT使用函数fftshift。

fft函数可直接计算信号的频谱，fftshift函数对频谱进行频移操作，将低频移到频谱中心。

四、Matlab中DFT及FFT频谱分析步骤1. 读取信号数据首先，将待分析的信号数据读入到Matlab中。

可以使用内置函数load读取文本文件中的数据，或通过自定义函数生成模拟信号数据。

2. 时域分析通过plot函数将信号数据在时域进行绘制，以观察信号的波形。

可以设置合适的坐标轴范围和标签，使图像更加清晰。

3. 信号预处理针对不同的信号特点，可以进行预处理操作，例如去除直流分量、滤波等。

这些操作可提高信号的频谱分析效果。

4. 计算DFT/FFT使用fft函数计算信号数据的DFT/FFT，并得到频谱。

将信号数据作为输入参数，设置采样频率和点数，计算得到频谱数据。

5. 频域分析通过plot函数将频谱数据在频域进行绘制，观察信号的频率特性。

可以设置合适的坐标轴范围和标签，使图像更加清晰。

6. 结果解读根据频谱图像，分析信号的频率成分、幅度分布和峰值位置。

离散傅⾥叶变换（DFT） 对于第⼀幅图来说，它侧重展⽰傅⾥叶变换的本质之⼀：叠加性，每个圆代表⼀个谐波分量。

第⼆幅图直观的表⽰了⼀个周期信号在时域与频域的分解。

周期信号的三⾓函数表⽰ 周期信号是每隔⼀定时间间隔，按相同规律⽆始⽆终重复变化的信号。

任何周期函数在满⾜狄利克雷条件下（连续或只有有限个间断点，且都是第⼀类间断点；只有有限个极值点），都可以展开成⼀组正交函数的⽆穷级数之和。

使⽤三⾓函数集的周期函数展开就是傅⾥叶级数。

对于周期为T 的信号f(t)，可以⽤三⾓函数集的线性组合来表⽰，即f(t)=a_0+\sum_{n=1}^{\infty }(a_n\cos n\omega t+b_n\sin n \omega t) 式中\omega=\frac{2\pi}{T}是周期信号的⾓频率，也成基波频率，n\omega称为n次谐波频率；a_0为信号的直流分量，a_n和b_n分别是余弦分量和正弦分量幅度。

根据级数理论，傅⾥叶系数a_0、a_n、b_n的计算公式为：\left\{\begin{matrix}a_0=\frac{1}{T}\int _{\frac{-T}{2}}^{\frac{T}{2}}f(t)dt \\ a_n=\frac{2}{T}\int _{\frac{-T}{2}}^{\frac{T}{2}}f(t)\cos{n\omegat}dt,n=1,2,3,... \\ b_n=\frac{2}{T}\int _{\frac{-T}{2}}^{\frac{T}{2}}f(t)\sin{n\omega t}dt,n=1,2,3,... \end{matrix}\right. 若将式⼦中同频率的正弦项和余弦项合并，得到另⼀种形式的周期信号的傅⾥叶级数，即f(t)=A_0+\sum_{n=1}^{\infty}A_n\cos(n\omega t+\varphi_n) 其中，A_0为信号的直流分量；A_1\cos(\omega t+\varphi_1)为信号的基频分量，简称基波；A_n\cos(n\omega t+\varphi_n)为信号的n次谐波，n ⽐较⼤的谐波，称为⾼次谐波。

实验三DFT和FFT频谱分析、实验目的1.掌握DFT频谱分析的原理与编程方法。

2.理解FFT算法的编程思想。

2.熟练掌握利用FFT对信号作频谱分析，包括正确地进行参数选择、画频谱及读频谱图。

3.利用FFT频谱分析进行快速卷积和太阳黑子周期性检测。

二、实验环境1.Windows xp以上操作系统2.安装MATLAB2007a 软件三、实验原理1.离散傅里叶变换(DFT)设序列为x(n),长度为N,则N 1X(ej 3 k)=DFT[x(n)]=送x(n) e-j o k n,n z02 n其中3 k= k(k=0,1,2, …-M,通常M>N,以便观察频谱的细节。

|X(ej 3 kH-x(n)的幅频谱。

M矚慫润厲钐瘗睞枥庑赖賃軔。

矚慫润厲钐瘗睞枥庑赖賃。

2.谱分析参数选择1)设信号x(t)最高频率为fc,对其进行取样得x(n),根据取样定理，取样频率fs必须满足: fs>=2fc。

聞創沟燴鐺險爱氇谴净祸測。

聞創沟燴鐺險爱氇谴净祸。

2)设谱分辨率为F,则最小记录时间tpmin=1/F ;取样点数N> 2fc/F为使用快速傅里叶变换(FFT)进行谱分析，N还须满足：N=2E (E为整数)。

3.用FFT计算信号x(n)的频谱。

［设x(n)为实信号］快速傅里叶变换(FFT)是DFT的一种快速算法，其使得DFT的运算速度大为加快。

1)对信号x(n)作N点FFT,得频谱X(k)(k=0~N-1)X(k)=XR(k)+jXI(k) (k=0~N/2-1)XR(k) — X(k)的实部；Xl(k) — X(k)的虚部。

残骛楼諍锩瀨濟2 / 12溆塹籟婭骤。

残骛楼諍锩瀨濟溆塹籟婭。

Matlab 语句：Y=fft(x,N) 其中：X----X (n );Y----X(k)』2 22)幅频谱:|X(k)|= V XR (K)+X I (K)， 由于x(n)为实信号，因此|X(k)|对称,Matlab 语句：abs(Y)iii)功率谱:PSD(k)=|X(k)|2/N=X(k)X*(k)/N Matlab 语句：PSD=Y .*conj(Y)/N其中：conj(Y)-- X*(k)[X(k) 的共轭]4.读频谱图频谱图中任意频率点k 对应实际频率为:fk=fs/N*k 。

第三章离散傅立叶变换(DFT)3．1 引言有限长序列在数字信号处理是很重要的一种序列，当然可以用Z变换和傅里叶变换来研究它，但是，可以导出反映它的"有限长"特点的一种有用工具是离散傅里叶变换(DFT)。

离散傅里叶变换除了作为有限长序列的一种傅里叶表示法在理论上相当重要之外，而且由于存在着计算离散傅里叶变换的有效快速算法，因而离散傅里叶变换在各种数字信号处理的算法中起着核心的作用。

有限长序列的离散傅里叶变换(DFT)和周期序列的离散傅里叶级数(DFS)本质上是一样的。

为了更好地理解DFT，需要先讨论周期序列的离散傅里叶级数DFS。

而为了讨论离散傅里叶级数及离散傅里叶变换，我们首先来回顾并讨论傅里叶变换的几种可能形式。

(连续时间信号：如果在讨论的时间间隔内，除若干不连续点之外，对于任意时间值都可给出确定的函数值，此信号就称为连续时间信号。

)一、连续时间、连续频率——连续傅立叶变换（FT）设x(t)为连续时间非周期信号，傅里叶变换关系如下图所示：可以看出时域连续函数造成频域是非周期的谱，而时域的非周期造成频域是连续的谱。

二、连续时间，离散频率------傅 里 叶 级 数设f(t)代表一个周期为T 1的周期性连续时间函数，f(t)可展成傅里叶级数，其傅里叶级数的系数为n F ，f(t)和n F 组成变换对，表示为:tjn n n e F t f 1)(Ω∞-∞=∑=（112Ω=πT ）dte tf T F TT t jn n ⎰-Ω-=221111)(1注意符号：如果是周期性的采样脉冲信号p(t)，周期用T 表示（采样间隔）。

采样脉冲信号的频率为Ts π2=Ω可以看出时域连续函数造成频域是非周期的谱，而时域的周期造成频域是离散的谱三、离散时间，连续频率------序列的傅里叶变换正变换：DTFT[x(n)]=()()j nj n X e x n eωω∞-=-∞=∑反变换：DTFT-11[()]()()2j n j j X e x n X e e d πωωωπωπ-==⎰)(ωj e X 级数收敛条件为|()j nn x n eω∞-=-∞∑|=∞<∑∞-∞=n n x )(可以看出时域离散函数造成频域是周期的谱，而时域的非周期造成频域是连续的谱四、离散时间，离散频率------离散傅里叶变换上面讨论的三种傅里叶变换对，都不适用在计算机上运算，因为至少在一个域(时域或频域)中，函数是连续的。

开课学院及实验室：电子楼3172018年 4月 29 日3()x n ：用14()()x n R n =以8为周期进行周期性延拓形成地周期序列.(1> 分别以变换区间N ＝8,16,32,对14()()x n R n =进行DFT(FFT>,画出相应地幅频特性曲线；(2> 分别以变换区间N ＝4,8,16,对x 2(n >分别进行DFT(FFT>,画出相应地幅频特性曲线； (3> 对x 3(n >进行频谱分析,并选择变换区间,画出幅频特性曲线.<二）连续信号 1. 实验信号：1()()x t R t τ=选择 1.5ms τ=,式中()R t τ地波形以及幅度特性如图7.1所示.2()sin(2/8)x t ft ππ=+式中频率f 自己选择.3()cos8cos16cos 20x t t t t πππ=++2. 分别对三种模拟信号选择采样频率和采样点数.对1()x t ()R t τ=,选择采样频率4s f kHz =,8kHz ,16kHz ,采样点数用τ.s f 计算.对2()sin(2/8)x t ft ππ=+,周期1/T f =,频率f 自己选择,采样频率4s f f =,观测时间0.5p T T =,T ,2T ,采样点数用p s T f 计算.图5.1 R(t>地波形及其幅度特性对3()cos8cos16cos 20x t t t t πππ=++,选择采用频率64s f Hz =,采样点数为16,32,64. 3. 分别对它们转换成序列,按顺序用123(),(),()x n x n x n 表示.4. 分别对它们进行FFT.如果采样点数不满足2地整数幂,可以通过序列尾部加0满足.5. 计算幅度特性并进行打印.五、实验过程原始记录<数据、图表、计算等）(一> 离散信号%14()()x n R n = n=0:1:10。

学生实验报告开课学院及实验室：电子楼3172013年4月29日、实验目的学习DFT 的基本性质及对时域离散信号进行频谱分析的方法，进一步加深对频域概念和数字频率的理解，掌握 MATLAB 函数中FFT 函数的应用。

二、实验原理离散傅里叶变换(DFT)对有限长时域离散信号的频谱进行等间隔采样，频域函数被离散化了, 便于信号的计算机处理。

设x(n)是一个长度为 M 的有限长序列，x(n)的N 点傅立叶变换:X(k)N 1j 三 knDFT[x(n)]N x(n)e N0 k N 1n 0其中WNe.2 jN，它的反变换定义为:1X(n)NkN 1nkX(k)W N0 令z W N k，X(zz WN k则有:N 1x( n)Wj kn 0可以得到，X(k)X(Z)Z WN kZ W N*是Z 平面单位圆上幅角为2kN 的点，就是将单位圆进行N 等分以后第 K 个点。

所以, X(K)是Z 变换在单位圆上的等距采样，或者说是序列傅立叶变换的等距采样。

时域采样在满足Nyquist 定理时，就不会发生频谱混叠。

DFT 是对序列傅立叶变换的等距采样，因此可以用于序列的频谱分析。

如果用FFT 对模拟信号进行谱分析，首先要把模拟信号转换成数字信号，转换时要求知道模拟 信号的最高截至频率，以便选择满足采样定理的采样频率。

般选择采样频率是模拟信号中最高频率的3~4倍。

另外要选择对模拟信号的观测时间，如果采样频率和观测时间确定，则采样点数也确定 了。

这里观测时间和对模拟信号进行谱分析的分辨率有关,最小的观测时间和分辨率成倒数关系。

最小的采样点数用教材相关公式确定。

要求选择的采样点数和观测时间大于它的最小值。

如果要进行谱分析的模拟信号是周期信号,最好选择观测时间是信号周期的整数倍。

如果不知道■ 厂1*1IE向i1A I1f Ii i 0r 1 疋0Jfb-4W0 70000图5.1 R(t)的波形及其幅度特性xn=[on es(1,4),zeros(1,7)];%输入时域序列向量 xn=R4( n)%计算xn 的8点DFTXk16=fft(x n,16);%计算xn 的16点DFTXk32=fft(x n,32); %计算xn 的32点DFTk=0:7;wk=2*k/8;对 x 3(t) cos8 t cos16 t cos20 t ，选择采用频率 f s 64Hz ，采样点数为 16 , 32 , 64。

matlab离散傅里叶变换幅值谱和相位谱离散傅里叶变换（Discrete Fourier Transform，DFT）是一种在信号处理和数字通信中常用的数学方法。

它可以将时间域或空间域的信号转换到频率域，从而揭示信号的频谱特性。

幅值谱和相位谱是DFT的两个重要组成部分，它们分别表示了信号在各个频率分量上的振幅和相位信息。

MATLAB是一款强大的数值计算工具，其内建函数可以实现离散傅里叶变换。

本文将介绍如何使用MATLAB进行离散傅里叶变换，并分析其幅值谱和相位谱。

一、离散傅里叶变换的实现MATLAB提供了fft()函数来实现离散傅里叶变换。

该函数的输入是一个时间序列数据或者空间图像数据，输出是一组复数结果，代表了每个频率分量的幅度和相位信息。

二、幅值谱分析幅值谱反映了信号在不同频率下的强度分布。

通过观察幅值谱，我们可以了解信号的主要成分以及它们的相对强度。

对于一个给定的信号，它的幅值谱可以由FFT的结果中的实部除以2得到。

如果我们对一幅图像数据进行傅里叶变换，那么得到的幅值谱将展示出图像的纹理和结构等信息。

三、相位谱分析相位谱描述了信号在各个频率处的相位信息。

通过对相位谱的分析，我们可以了解信号的时域特征，比如周期性、非周期性和噪声等。

一般来说，相位的变化范围是从-π到+π，其中负数的出现通常意味着信号存在某种扭曲或失真。

对于一幅图像数据的相位谱，可以看到的是像素点之间的相对位置关系，这对于理解和解释图像内容非常有帮助。

下面是一个简单的示例代码：【示例】% 假设我们有一组时间序列数据x = [x1, x2, ..., xN];【示例】% 首先使用MATLAB内置的fft()函数对其进行傅里叶变换Y = fft(x);【示例】% 然后可以得到频谱的高频部分，对应于振幅zui大的频率分量，记为A(0);freq = Y(1:N/2+1);amp = abs(freq)/N; % 注意除以N是因为采样点的数量会影响jue对值的准确度;Amplitude = mean(amp);fprintf('zui大频率的振幅是%.2f\n', Amplitude);【示例】% 使用双精度浮点数存储相位会使得位数过多而难以阅读和理解，因此可以使用双精度小数来显示低精度的部分以供参考;phase = angle(Y(1:N/2));fprintf('高频部分的相位为%.5lfi\n', phase/(2*pi)); % 注意'%lfi'用于显示双精度小数的低精度部分，这段代码可以帮助你理解如何使用MATLAB进行离散傅里叶变换及其相关的分析和应用。

实验二 离散信号与系统的频谱分析一、实验目的1.掌握离散傅里叶变换（DFT ）及快速傅里叶变换（FFT ）的计算机实现方法。

2.检验序列DFT 的性质。

3.掌握利用DFT （FFT ）计算序列线性卷积的方法。

4.学习用DFT 对连续信号和时域离散信号进行谱分析的方法，了解可能出现的分析误差，以便在实际中正确应用DFT 。

5.了解采样频率对谱分析的影响。

6.了解利用FFT 进行语音信号分析的方法。

二、实验设备1.计算机2.Matlab 软件7.0以上版本。

三、实验内容1.对不同序列进行离散傅里叶变换并进行分析；DFT 共轭对称性质的应用（通过1次N 点FFT 计算2个N 点实序列的DFT ）。

2.线性卷积及循环卷积的关系，以及利用DFT （FFT ）进行线性卷积的方法。

3.比较计算序列的DFT 和FFT 的运算时间。

4.利用FFT 实现带噪信号检测。

5.利用FFT 计算信号频谱及功率谱。

6.扩展部分主要是关于离散系统采样频率、时域持续时间、谱分辨率等参数之间的关系，频谱的内插恢复，对语音信号进行简单分析。

四、实验原理1.序列的离散傅里叶变换及性质离散傅里叶变换的定义：10, )()]([)(102-≤≤==∑-=-N k en x n x DFT k X N n nk Nj π离散傅里叶变换的性质：（1）DFT 的共轭对称性。

若)()()(n x n x n x op ep +=，[])()(n x DFT k X =，则：)()]([k X n x DFT R ep =， )()]([k jX n x DFT I op =。

（2）实序列DFT 的性质。

若)(n x 为实序列，则其离散傅里叶变换)(k X 为共轭对称，即10),()(*-≤≤-=N k k N X k X 。

（3）实偶序列DFT 的性质。

若)(n x 为实偶序列，则其离散傅里叶变换)(k X 为实偶对称，即10),()(-≤≤-=N k k N X k X 。

FFT谱分析实验报告1. 引言谱分析是一种常见的信号处理技术，用于将一个信号分解为不同频率的成分。

FFT（快速傅里叶变换）是一种高效的算法，用于计算离散傅里叶变换，广泛应用于谱分析中。

本实验旨在探究FFT在信号处理中的应用，并通过实验验证其有效性。

2. 实验目的本实验旨在： - 理解FFT算法的原理和实现方法； - 学习如何使用FFT对信号进行频谱分析； - 验证FFT算法的准确性和有效性。

3. 实验步骤3.1 准备实验材料和工具为了进行谱分析实验，我们需要准备以下材料和工具： - 信号源（例如音频文件、信号发生器等） - 电脑（用于运行信号处理软件） - 信号处理软件（例如MATLAB、Python等）3.2 选择信号源在本实验中，我们选择了一个音频文件作为信号源。

音频文件包含了不同频率的声音信号，适合用于谱分析。

3.3 导入信号源使用信号处理软件，将选择的音频文件导入到程序中。

3.4 实施FFT算法根据FFT算法的原理，我们可以使用信号处理软件实施FFT算法。

以下是实施FFT算法的步骤： 1. 对导入的音频信号进行采样。

2. 将采样后的信号进行傅里叶变换，得到信号的频域表示。

3. 可选地，对频域表示进行滤波或其他信号处理操作。

4. 将处理后的信号进行逆傅里叶变换，得到恢复后的信号。

3.5 分析结果通过实施FFT算法，我们得到了信号的频域表示。

可以通过绘制频谱图来直观地观察信号的频率成分。

频谱图通常以频率为横轴，幅度为纵轴。

通过观察频谱图，我们可以分析信号中存在的频率成分及其强度。

3.6 结果验证为了验证FFT算法的有效性，我们可以选择一些已知频率的信号作为测试样本。

通过对测试样本进行FFT分析，并与已知频率进行比较，可以评估FFT算法的准确性。

4. 结果与讨论通过实验，我们成功使用FFT算法对音频信号进行了谱分析。

通过观察频谱图，我们可以清楚地看到信号中存在的频率成分。

在结果验证部分，我们与已知频率进行了比较，结果表明FFT算法具有较高的准确性。