离散傅里叶变换及其快速算法

离散傅里叶变换及其快速算法离散傅里叶变换（Discrete Fourier Transform，DFT）是一种将离散信号转换为频域表示的数学工具。

它在信号处理、图像处理、通信等领域有广泛的应用。

而快速傅里叶变换（Fast Fourier Transform，FFT）是一种能够高效计算DFT的算法，大大减少了计算量。

首先，我们来看一下DFT的原理。

给定一个有限长度的离散信号序列x(n)，DFT将其转换为频谱X(k)，其中k为频率索引，取值范围为0到N-1，N为序列的长度。

DFT的定义公式如下：X(k) = Σ x(n) * exp(-j * 2π * nk / N)其中，exp为自然指数函数，j为虚数单位。

DFT将信号分解为了N个复数的和，这些复数代表了不同频率分量在信号中的贡献。

然而，直接计算DFT的时间复杂度非常高，为O(N^2)。

为了提高计算效率，Cooley和Tukey于1965年提出了FFT算法。

FFT算法基于以下性质：若N为2的整数次幂，则DFT可以被分解为两个较小长度的DFT的线性组合。

具体来说，将N个点的DFT拆分为长度为N/2的两个DFT，然后再对这两个子序列进行DFT，最后将两个子序列的结果组合起来。

这个过程可以递归地进行，直到序列长度为1，即可得到最终的DFT结果。

FFT算法的时间复杂度为O(NlogN)，远远小于直接计算DFT的复杂度。

这使得FFT成为了处理大规模数据的首选方法之一、此外，FFT还有其他一些优点，如可并行化计算、对称性质等。

FFT算法可以采用不同的实现方式，最著名的是基于蝶形运算的Cooley-Tukey算法。

这种实现方式将FFT过程分为了两个阶段：置换阶段和蝶形运算阶段。

置换阶段通过将信号重新排序，将原始序列分为奇偶两个子序列，并计算每个子序列的DFT。

这个过程可以递归地应用于子序列，直到长度为1蝶形运算阶段是FFT算法的核心部分。

蝶形运算是指将两个频域上的复数进行运算，得到新的复数。

fft计算公式摘要：一、引言二、FFT 计算公式简介1.离散傅里叶变换2.快速傅里叶变换三、FFT 计算公式推导1.基2 递归算法2.蝴蝶运算四、FFT 在实际应用中的优势五、总结正文：一、引言在数字信号处理、图像处理等领域，傅里叶变换是一种非常重要的数学工具。

然而，对于大规模的信号处理问题，直接应用傅里叶变换的计算复杂度较高，因此，快速傅里叶变换（FFT）应运而生。

本文将详细介绍FFT 的计算公式及应用。

二、FFT 计算公式简介为了便于理解FFT 的计算公式，我们先简要介绍一下离散傅里叶变换（DFT）和快速傅里叶变换（FFT）。

1.离散傅里叶变换（DFT）DFT 是一种将离散信号从时域转换到频域的方法，其计算公式如下：X[k] = ∑N/2^n i^(-k+n) * x[n]其中，X[k] 表示频域的系数，x[n] 表示时域的信号，k 和n 分别为频域和时域的下标，N 为信号长度。

2.快速傅里叶变换（FFT）FFT 是DFT 的高效实现方法，它采用分治策略和循环移位技术，将DFT 的计算复杂度从O(N^2) 降低到O(NlogN)。

FFT 的计算公式如下：X[k] = ∑(N/2^n)^(2m) * C[m, k] * x[n]其中，m 为迭代次数，k 和n 分别为频域和时域的下标，N 为信号长度，C[m, k] 为复合基函数。

三、FFT 计算公式推导为了更直观地理解FFT 的计算过程，我们分两步进行推导。

1.基2 递归算法（1）首先，将输入序列x[n] 进行零填充，使其长度变为2 的整数次幂，即N = 2^n。

（2）将x[n] 和x[n+N/2] 进行旋转，得到x[n] 和x[n+N/2]，其中x[n] 为原始序列，x[n+N/2] 为旋转后的序列。

（3）对旋转后的序列进行DFT 计算，得到频域系数X[k] 和X[k+N/2]。

（4）根据旋转序列的关系，可以得到频域系数X[k+N/2] = X[k]，因此，我们只需计算一半的频域系数。

傅里叶变换及其快速算法傅里叶变换是一种重要的信号分析工具，它在多个领域中被广泛应用，包括图像处理、音频处理、通信系统等等。

本文将介绍傅里叶变换的基本原理，并详细探讨其快速算法。

一、傅里叶变换的基本原理傅里叶变换是将一个信号表示为频域的复振幅和相位的分析工具。

它能够将一个连续时间域信号转换为连续频域信号，通过分析信号的频谱信息来揭示信号的特征和特性。

傅里叶变换的表达式如下：\[ F(\omega) = \int_{-\infty}^{\infty} f(t)e^{-j\omega t}dt \]其中，\(F(\omega)\)表示信号的频谱，\(f(t)\)表示信号在时域的函数。

二、离散傅里叶变换在数字信号处理中，我们通常处理离散时间域的信号。

离散傅里叶变换（DFT）是傅里叶变换在离散时间域上的推广。

DFT的表达式如下：\[ F[k] = \sum_{n=0}^{N-1} f[n]e^{-j\frac{2\pi}{N}kn} \]其中，\(F[k]\)表示信号的频谱，\(f[n]\)表示信号在时域的离散序列，\(N\)表示序列的长度，\(k\)表示频率的序号。

三、快速傅里叶变换DFT的计算复杂度为\(O(N^2)\)，当信号长度较大时，计算量将非常巨大。

为了解决这个问题，提出了快速傅里叶变换（FFT）算法，能够将计算复杂度降低到\(O(N\log N)\)。

FFT算法基于分治法，将信号分解为较小的子问题，然后进行逐层合并。

其基本思想是通过迭代和递归的方式将DFT计算变为多个较小规模的DFT计算。

常用的FFT算法有蝶形算法（Butterfly Algorithm）和Cooley-Tukey 算法。

蝶形算法是一种基于时域采样点的折叠和重叠计算的方法；Cooley-Tukey算法则是一种使用递归分治的迭代算法。

FFT算法的快速计算使其得到了广泛的应用，特别是在实时系统和大规模数据处理中。

四、应用领域傅里叶变换及其快速算法在各个领域都有着广泛的应用。

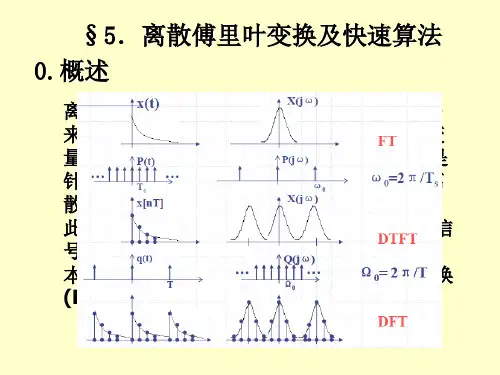
第五章 离散傅里叶变换及其快速算法 1 离散傅里叶变换(DFT)的推导(1) 时域抽样：目的：解决信号的离散化问题。

效果：连续信号离散化使得信号的频谱被周期延拓。

(2) 时域截断：原因：工程上无法处理时间无限信号。

方法：通过窗函数(一般用矩形窗)对信号进行逐段截取。

结果：时域乘以矩形脉冲信号，频域相当于和抽样函数卷积。

(3) 时域周期延拓：目的：要使频率离散，就要使时域变成周期信号。

方法：周期延拓中的搬移通过与)(s nT t -δ的卷积来实现。

表示：延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。

结果：周期延拓后的周期函数具有离散谱。

(4)1。

图1 DFT 推导过程示意图(5) 处理后信号的连续时间傅里叶变换：∑∑∞-∞=-=π--δ⋅⎥⎥⎦⎤⎢⎢⎣⎡=k N n N kn j s kf f e nT h f H )()()(~010/2(i))(~f H 是离散函数，仅在离散频率点SNT kT k kf f ===00处存在冲激，强度为k a ，其余各点为0。

(ii) )(~f H 是周期函数，周期为ss T NT N T N Nf 100===，每个周期内有N 个不同的幅值。

(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。

2 DFT 及IDFT 的定义(1) DFT 定义：设()s nT h 是连续函数)(t h 的N 个抽样值1,,1,0-=N n ，这N 个点的宽度为N 的DFT 为：[])1,...,1,0(,)()(10/2-=⎪⎪⎭⎫⎝⎛==∆-=π-∑N k NTk H enT h nT h DFT s N n Nnk j s s N (2) IDFT 定义：设⎪⎪⎭⎫⎝⎛s NT kH 是连续频率函数)(f H 的N 个抽样值1,,1,0-=N k ， 这N 个点的宽度为N 的IDFT 为：())1,...,1,0(,110/21-==⎪⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛∆-=π--∑N k nT h e NTkH NNT kH DFT s N k N nk j s sN (3) N nk j e /2π-称为N 点DFT 的变换核函数，N nk j e /2π称为N 点IDFT 的变换核函数。

用Fourier 变换来表示序列和线性时不变系统的频域特征，但是频谱()ωj e X 是ω的连续函书，用计算机处理和分析频谱是不方便的。

那么就需要像时序信号那样，通过采集把连续信号变为离散信号，也对连续频谱采样而得到离散频谱，然后用数字电路或计算机进行处理和分析。

有限长序列在应用中有重要的作用，通过它可以导出另一种Fourier 变换表达式，即离散傅里叶变换(DFT)，此为解决频谱离散化的有效方法，同时DFT 的高效算法——快速傅里叶变换FFT 。

周期序列一个周期为N 的周期序列~x ，对于所有的n ，应该满足：()()为整数k kN n x x +=~~周期序列的周期N ，一般使用最小周期作为周期。

与连续时间周期函数相比，周期序列由于n 及N 均为整数，周期序列中应用最广泛的序列是：kn Njkn NeWπ2-=（2-1）ImRe1上图就是周期序列nN W （N=8），从n=0开始到8取完周期内的所有值。

令k = 1时，nN W 就是一个周期序列。

当n 从0依次加1到N-1时，序列nN W 取完周期内的所有值，这些值可以看成是Z 平面上以原点为圆心的单位圆被N 等分的交点的的坐标值。

k 为其他数值时，knN W 的最小周期也许不是N ，但是N 一定是knN W 的周期。

knN W 的性质很明显：周期性：knN W =nN k NW )(-=)(N n k NW -对称性：kn N W -=()*kn N W =nk N NW )(-=)(n N k NW -正交性：()()∑-=⎩⎨⎧==10n 0,N k knNr rN n N W其他为整数 或者 ()()∑-=⎩⎨⎧==1n 0,N n kn Nr rN k N W其他为整数 一个周期为N 的周期序列()n x ~，在n=∞-到n=+∞的范围内仅有N 个序列值是独立的其中一个周期内的N 个序列值足以表征整个序列的特征。

而对于长度为N 的有限长序列，只讨论n=0到N-1之间的N 个序列值，其余皆为0。