如何用圆规画椭圆

圆规不规则形的构造与测量圆规是一种常见的绘图工具，常用于画弧和测量长度。

它由两个可移动的腿部组成，其中一个腿部带有一支锐尖，另一个腿部有一个可移动的铅笔。

在绘图中，我们通常会遇到一些不规则形状，如椭圆、双曲线等。

本文将介绍如何使用圆规构造和测量这些不规则形状。

一、构造椭圆椭圆是一个有两个焦点的平面曲线，其到两个焦点的距离之和是常数。

使用圆规可以简便地构造一个椭圆。

步骤：1. 在纸上画一条任意长的线段AB，并取线段的中点C。

2. 以C为圆心，以CA长度为半径，画一条弧交线段AB于点D。

3. 保持圆规张开的距离不变，将一只腿部放在点C上。

4. 以点D为焦点，以线段CD的长度为半径，画一条弧交线段AB 于点E。

5. 连接点D、E和C，得到的曲线为椭圆。

二、构造双曲线双曲线是一个与两个焦点有关的平面曲线，其到两个焦点的距离之差是常数。

使用圆规也可以简便地构造一个双曲线。

步骤：1. 在纸上画一条任意长的线段AB，并取线段的中点C。

2. 以C为圆心，以CA长度为半径，画一条弧交线段AB于点D。

3. 保持圆规张开的距离不变，将一只腿部放在点C上。

4. 以点D为焦点，以线段CD的长度为半径，画一条弧交延长线段AB于点E。

5. 保持圆规张开的距离不变，将一只腿部放在点E上。

6. 以点D为焦点，以线段DE的长度为半径，画一条弧交延长线段AB于点F。

7. 连接点D、F和C，得到的曲线为双曲线。

三、测量不规则形状的长度除了用于构造不规则形状，圆规还可以用于测量其长度。

以下是使用圆规测量长度的方法：步骤：1. 将圆规一个腿部的锐尖放在不规则形状的起点。

2. 将圆规另一只腿部拖动，直到触及不规则形状的边界上的一点。

3. 将圆规保持张开的状态，将另一只腿部上的铅笔与不规则形状的路径对齐。

4. 保持圆规的张开状态，将圆规放在直尺上，测量圆规两腿部之间的距离。

5. 得到的测量值即为不规则形状的长度。

总结：圆规是一种多功能的绘图工具，不仅可以用于构造和测量规则形状，还可以用于不规则形状的构造和测量。

如何用圆规画椭圆
1.做垂直相交的2条直线，在上面确定A、B、C、
D、O五个点，AB为长轴，CD为短轴，O为中心点
2.连接AC
3.以O为圆心，OA的长为半径画圆，交CD线于E点
4.以C为圆心，CE的长为半径画圆，交AC线于F点
5. 以A为圆心，AF的长为半径画圆
7.连接GH，交AB轴于O1点，交CD轴于O2点
8．以O为圆心，OO1的长为半径画圆，交OB 于O3点
（为了避免太多字母看的晕，下面不必要的点就没有标注字母了）
9. 以O为圆心，OO2的长为半径画圆，交OB 于O4点
10. 以O1为圆心，O1A的长为半径画圆
11. 以O3为圆心，O3B的长为半径画圆
12. 以O2为圆心，O2C的长为半径画圆
13. 以O4为圆心，O4D的长为半径画圆。

圆规的用法如何使用圆规圆规在数学和制图里，是用来绘制圆或弦的工具，常用于尺规作图。

而圆规有哪些使用方法呢?以下是由店铺整理关于圆规的用法的内容，希望大家喜欢!圆规的用法1、用尺子量出圆规两脚之间的距离，作为半径。

2、把带有针的一端固定在一个地方，作为圆心。

3、把带有铅笔的一端旋转一周。

使用圆规的注意事项1、圆规两脚之间的高度要一样。

2、画圆的过程中圆规要稍微倾斜30度左右，使画出的圆的线条流畅。

3、画圆的过程中带有针的一端(即圆心)不能移动。

4、画圆的过程中两脚距离(即半径)不能改变。

5、绘图时小心针刺到手。

圆规的发明圆规的发明最早可追溯至中国夏朝，《史记·夏本记》载大禹治水“左凖绳，右规距”，公元前15世纪的甲骨文中，已有规、矩二字，当时称为“ 规”，即今日的圆规，《周礼·考工记·匠人》记载：“匠人建国，平地以悬，置槷以悬，视以景。

为规，识日出之景与日入之景。

昼参诸日中之景，夜考之极星，以正朝夕。

”。

山东嘉祥武梁祠内有“东汉伏羲女娲砖刻像”，其中女娲执规，伏羲执矩，这里的规是古式梁规，形状与甲骨文“癸”的字形相似。

绘圆用的绘图工具。

有两只脚，上端铰接，下端可随意分开或合拢，以调整所绘圆弧半径的大小。

一只脚的末端为针尖，另一只脚的末端可装入绘铅笔线或墨线的脚。

有的圆规装上延伸杆，可画出较大的圆。

有梁规、弹簧小圆规和活心小圆规等。

圆规的结构圆规由笔头、转轴、圆规支腿、格尺、折叶、笔体、笔尖、圆规尖、小耳构成，它的笔头的下端插入连接在笔体的上端，笔体的下端螺纹连接在笔尖的上端，小耳的平齐端焊接在圆规支腿的外侧中间，圆规支腿的下端夹紧连接在圆规尖的上端。

其特征是：笔体的一面粘贴连接在折叶的一面，折叶的另一面粘贴连接在格尺的一端中间，笔体的夹缝上端两侧插入连接在转轴的两端，转轴的轴体穿套连接在圆规支腿的上端。

如何用圆规画椭圆椭圆是数学中的一个几何图形，它在几何学、力学、天文学等领域中都有广泛的应用。

圆规是一种画图工具，用来测量和绘制圆和弧线。

通过正确的使用圆规，我们可以画出一个完美的椭圆。

首先，让我们了解一下椭圆的基本知识。

椭圆是一个平面上的图形，定义为平面上到两个固定点（焦点）的距离之和等于常数的点的轨迹。

这两个固定点被称为焦点，通常用字母F1和F2表示。

椭圆上任意一点到这两个焦点的距离之和等于常数，可以表示为2a，其中a是椭圆的半长轴的长度。

为了用圆规画出椭圆，我们需要知道椭圆的半长轴(a)和半短轴(b)的长度。

在画椭圆之前，我们需要准备好以下工具：一组圆规、一支铅笔和一张纸。

第一步是确定椭圆的中心点。

在纸上选择一个点作为椭圆的中心点，命名为O。

第二步是确定椭圆的半长轴(a)和半短轴(b)的长度。

以中心点为基准，使用圆规测量出椭圆的半长轴的长度，并将圆规的一只脚尖放在中心点上，另一只脚尖放在椭圆上，这个值就是半长轴的长度。

然后将这个长度记录下来。

接下来，使用圆规从中心点画一条线段，长度为半长轴的长度。

第三步是确定椭圆的焦点。

将圆规的一只脚尖放在椭圆的中心点上，另一只脚尖上移到椭圆上方的半短轴的长度上。

将这个点命名为F1、然后再将另一只脚尖向下移到椭圆下方的半短轴的长度上。

将这个点命名为F2、这两个点就是椭圆的焦点。

第四步是画椭圆的路径。

将圆规的一只脚尖放在中心点O上，另一只脚尖放在一条标记在半长轴线上的点上。

然后将圆规的脚尖上移到椭圆的焦点F1上，再将圆规的脚尖移到椭圆的焦点F2上，画出一个弧线。

接着，将圆规的脚尖放在椭圆焦点F2上，将圆规的脚尖移到标记在半长轴线上的另一个点上，再将圆规的脚尖移到椭圆的焦点F1上，画出第二个弧线。

重复这个过程，直到完成整个椭圆的路径。

可以看到，通过正确使用圆规，我们可以画出一个完整的椭圆的轮廓。

画椭圆需要一定的准确度和耐心，所以需要练习和反复的试验。

在实际应用中，我们也经常会遇到需要调整椭圆的尺寸和比例的情况。

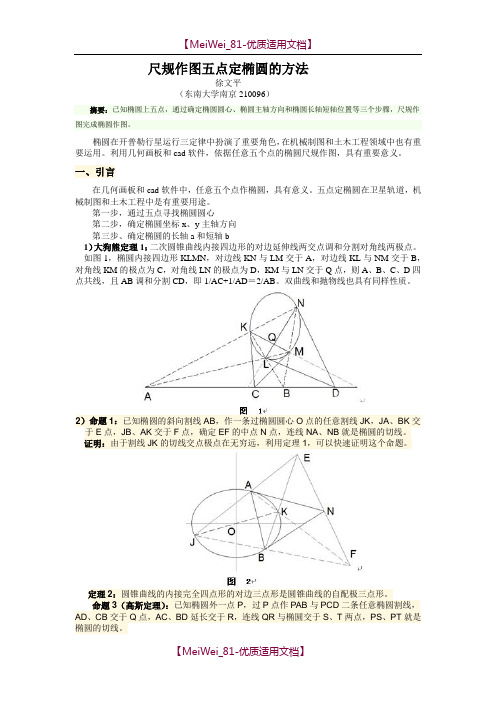
尺规作图五点定椭圆的方法徐文平（东南大学南京210096）摘要：已知椭圆上五点，通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤，尺规作图完成椭圆作图。

椭圆在开普勒行星运行三定律中扮演了重要角色，在机械制图和土木工程领域中也有重要运用。

利用几何画板和cad软件，依据任意五个点的椭圆尺规作图，具有重要意义。

一、引言在几何画板和cad软件中，任意五个点作椭圆，具有意义。

五点定椭圆在卫星轨道，机械制图和土木工程中是有重要用途。

第一步，通过五点寻找椭圆圆心第二步，确定椭圆坐标x、y主轴方向第三步、确定椭圆的长轴a和短轴b1）大狗熊定理1：二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。

如图1，椭圆内接四边形KLMN，对边线KN与LM交于A，对边线KL与NM交于B，对角线KM的极点为C，对角线LN的极点为D，KM与LN交于Q点，则A、B、C、D四点共线，且AB调和分割CD，即1/AC+1/AD＝2/AB。

双曲线和抛物线也具有同样性质。

2）命题1：已知椭圆的斜向割线AB，作一条过椭圆圆心O点的任意割线JK，JA、BK交于E点，JB、AK交于F点，确定EF的中点N点，连线NA、NB就是椭圆的切线。

证明：由于割线JK的切线交点极点在无穷远，利用定理1，可以快速证明这个命题。

定理2：圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。

命题3（高斯定理）：已知椭圆外一点P，过P点作PAB与PCD二条任意椭圆割线，AD、CB交于Q点，AC、BD延长交于R，连线QR与椭圆交于S、T两点，PS、PT就是椭圆的切线。

图3二、通过五点寻找椭圆圆心原理：通过已知五点，作椭圆切线，获得割线的极点，将割线的极点和割线中点连接并延伸，必定通过椭圆的圆心。

图4问题1：只有五点，没有坐标轴和原点，椭圆斜的，割线PQ的切线极点如何办？切线方法：帕斯卡定理（五点+一个切点二次）做切线，或者如图5方法作切线。

椭圆的绘制方法
宝子，今天咱来唠唠椭圆咋画哈。

一种简单的方法呢，就是用一根绳子和两个钉子。

先找块木板或者厚纸板啥的，在上面钉两个钉子，这两个钉子的距离可不能太近也不能太远哦。

然后拿根绳子，把绳子的两头分别系在这两个钉子上，绳子要松松垮垮地系着，可不能系太紧啦。

接着拿支笔，把绳子绷紧，就像拉着小皮筋一样，然后让笔靠着绳子绕着这两个钉子画圈，嘿一个椭圆就出来啦。

这就像是给两个钉子之间拉了个特殊的轨道，笔就沿着这个轨道跑，跑出个椭圆来呢。

还有一种办法，要是你有圆规的话，也能画个大概的椭圆哦。

不过这个就有点小技巧啦。

先画一个圆，然后在这个圆的基础上，把圆规的脚稍微往圆心方向挪一点，再画一段弧，接着再从另外的方向挪一点再画弧，就这样一点点地画，最后也能拼凑出个椭圆的样子。

虽然这个椭圆可能不是特别标准，但是也有点椭圆的那个味儿啦，就像小娃娃学走路，虽然走得歪歪扭扭，但也能到目的地呢。

要是你用电脑软件画椭圆，那就更简单啦。

比如说在画图软件里，一般都有专门画椭圆的工具，你就像点小按钮一样点一下，然后在画布上拉一拉，想让椭圆胖一点就拉宽一点，想让椭圆瘦一点就拉长一点，就跟捏橡皮泥似的，超级方便。

这就像是魔法一样，一下子椭圆就出现在屏幕上啦。

宝子，你要是想画个好看的椭圆，就可以试试这些方法哦。

不管是手工的还是用软件的，都能让你画出椭圆来。

要是画得不太好也没关系呀，多试几次就好啦，就像学骑自行车，摔几跤就学会啦，加油哦。

。

机械制图公开课教案（椭圆的画法）第一章：椭圆的基本概念1.1 椭圆的定义让学生了解椭圆的定义，即椭圆是一个平面上到两个固定点（焦点）距离之和为常数的点的集合。

1.2 椭圆的性质讲解椭圆的性质，包括椭圆的长轴、短轴、焦距、离心率等。

1.3 椭圆的标准方程引导学生推导椭圆的标准方程，并理解其含义。

第二章：椭圆的画法2.1 椭圆的简单画法介绍椭圆的简单画法，如利用圆规和直尺画椭圆。

2.2 椭圆的焦点画法讲解利用椭圆的焦点画椭圆的方法，包括焦点法、直角坐标法等。

2.3 椭圆的参数方程画法介绍椭圆的参数方程画法，让学生了解如何利用参数方程来绘制椭圆。

第三章：椭圆在机械制图中的应用3.1 椭圆在零件设计中的应用讲解椭圆在机械零件设计中的应用，如轴承、齿轮等。

3.2 椭圆在机械装配中的应用介绍椭圆在机械装配中的应用，如椭圆形的配合面、运动轨迹等。

3.3 椭圆在其他领域的应用引导学生了解椭圆在其他领域的应用，如天文学、工程设计等。

第四章：椭圆的计算4.1 椭圆的长轴和短轴计算讲解如何计算椭圆的长轴和短轴，以及它们与焦距、离心率的关系。

4.2 椭圆的面积计算介绍如何计算椭圆的面积，以及面积与长轴、短轴的关系。

4.3 椭圆的周长计算讲解如何计算椭圆的周长，以及周长与长轴、短轴的关系。

第五章：椭圆在实际问题中的应用5.1 椭圆在工程设计中的应用让学生了解椭圆在工程设计中的应用，如椭圆形桥梁、汽车车身等。

5.2 椭圆在天文学中的应用讲解椭圆在天文学中的应用，如行星运动轨迹、卫星轨道等。

5.3 椭圆在其他领域的应用引导学生了解椭圆在其他领域的应用，如生物学、艺术设计等。

第六章：椭圆的变换6.1 椭圆的平移讲解如何对椭圆进行平移，让学生掌握椭圆平移的规律和方法。

6.2 椭圆的旋转介绍如何对椭圆进行旋转，以及旋转对椭圆形状和大小的影响。

6.3 椭圆的缩放讲解如何对椭圆进行缩放，以及缩放对椭圆形状和大小的影响。

第七章：椭圆的计算机辅助设计7.1 椭圆CAD软件的基本操作介绍椭圆CAD软件的基本操作，如创建、编辑、绘制椭圆等。

圆规画椭圆最简单方法Drawing an ellipse with a compass is often considered a challenge due to its complex shape. However, there are simple methods that can be used to achieve this. One common approach is to use the two-focus method, in which a string is looped around two fixed points and pulled taut to form an ellipse. This technique can be a bit tricky to master at first, but with practice, it can produce accurate results.用圆规画椭圆通常会被认为是一项挑战，因为其复杂的形状。

然而，有一种简单的方法可以实现这个目标。

一个常见的方法是使用两个焦点法，通过在两个固定点之间绕上一根绳子，并拉紧形成椭圆。

这种技术一开始可能有点难以掌握，但通过实践，可以产生准确的结果。

When using the two-focus method, it's important to ensure that the two fixed points are accurately positioned to replicate the shape of an ellipse. The distance between the two foci will determine the length and shape of the resulting ellipse. By adjusting the tension of the string and the position of the fixed points, one can experiment with different ellipse shapes and sizes.在使用两焦点法时，确保两个固定点的位置准确是很重要的，以便复制椭圆的形状。