重叠部分图形的面积专题
- 格式:ppt
- 大小:683.00 KB
- 文档页数:39
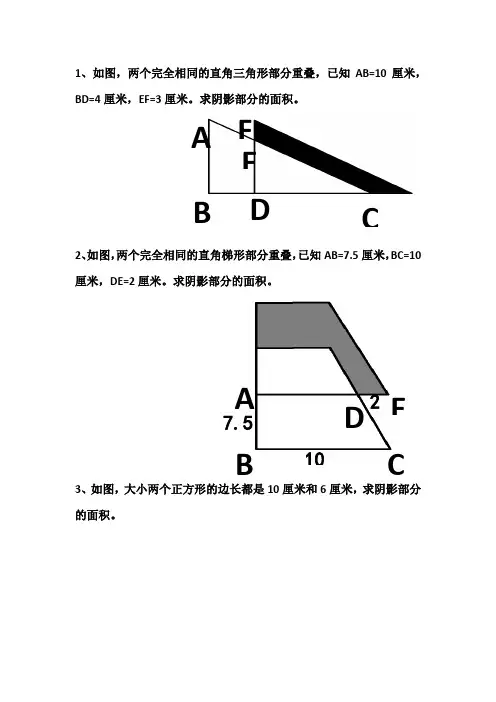
1、如图,两个完全相同的直角三角形部分重叠,已知AB=10厘米,BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
ABCDEFADEBC107.524、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?ABCDEFABCDFEG7、如图,梯形上底长5.4厘米,下底长8.6厘米,高长4厘米,求三角形甲的面积比三角形乙的面积小多少平方厘米?8、如图,ABCD 是长方形,AB=8厘米,BC=6厘米,三角形ABF 的面积比三角形DEF 的面积大12平方厘米,求DE 长多少厘米?9、如图,平行四边形ABCD 的底BC 长10厘米,直角三角形FBC 的直角边FC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10平方厘米。
求EF 的长度。
甲乙ABCDEF8681010、如图,△ABC 和△DCB 都是直角三角形,已知AB=3.4厘米,BC=7.2厘米,且甲比乙的面积大3.6平方厘米,求CD 的长。
11、如图,CA=AB=4厘米,三角形ABE 的面积比三角形CDE 的面积小2平方厘米,求CD 的长。
12、如图,甲的面积比乙的面积大36平方厘米,已知AB 长8厘米,BC 长12厘米,CD 长6厘米,求DE 的长。
ABCD甲乙7.23.4ABCDE4ABCDE 甲乙812613、如图,D 是AC 的中点,E 、F 是BC 边上的三等分点,已知阴影部分的面积为20平方厘米,求三角形ABC 的面积。

图形面积巧计算专项练习 (附解题思路和参考答案)教学内容:巧算图形面积。
教学对象:三、四年级学生。
教学重点:正方形、长方形面积的计算。
教学难点:重叠图形面积的计算。
教学过程: 一 复习教学(一)点学生回答:1.什么叫面积?2.正方形、长方形的公式、3.遇到较复杂的组合图形后又该如何计算?(二)投影出示下列内容,引导学生熟读记牢。
1面积:面积指的是物体所占平面的大小。
2 长方形的面积=长×宽,长方形的面积÷长=宽,长方形的面积÷宽=长。
正方形的面积=边长×边长,正方形的面积÷边长=边长。
3 求复杂图形的面积,需要敏锐的观察力和灵活的思维,运用添加辅助线、割补、转化等方法解答。
二新课教学(一)例题1 在一张长9米,宽7米的长方形铁板上,切割出一个面积最大的正方形,这个正方形铁板的面积是多少平方米?三 巩固练习11. 明明把一张长12厘米,宽8厘米的长方形纸剪成一个面积最大的正方形,这张正方形纸的面积是多少平方厘米?请根据例题写出解题思路:请列式计算9米 7 米 解题思路:要使切割出的正方形铁板面积最大就要使它的边长最长(如图),那么只能选原来的长方形的宽为边长,即正方形的边长为7米。
解:7×7=49(平方米) 答:这个正方形铁板的面积是49平方米。
2 妈妈把一块长2米,宽6分米的长方形布料裁成一个面积最大的正方形,这个正方形的面积是多少?解题思路: 1. 统一单位:2米=20分米。
2. 再根据正方形的面积公式“边长×边长”可求出基面积。
解:3 将以张长10米,宽8米的长方形铁板切割成一个面积最大的正方形,这个正方形的面积是多少平方米?剩下的部分是什么形状?面积是多少?1.正方形的面积:答:这个正方形的面积是 平方米。
2.剩下的面积:答;剩下的部分是 ,面积是 平方米。
(二)例题2 求下面图形的面积。
(单位:厘米)解题思路:不是规则的长方形要把原图进行割补,使其变成规则的图形解答。

重叠法的经典例题一、例题在一个长方形中,长为8厘米,宽为6厘米,有两个半径为1厘米的圆重叠放在长方形内(圆与长方形的边相切),求阴影部分(两个圆重叠部分以外的区域)的面积。
二、题目解析1. 首先计算长方形的面积- 根据长方形面积公式S = a× b(其中a为长,b为宽),已知长方形长a = 8厘米,宽b = 6厘米,所以长方形面积S_长方形=8×6 = 48平方厘米。
2. 然后计算两个圆的面积- 根据圆的面积公式S=π r^2(其中r为半径),已知圆半径r = 1厘米,一个圆的面积S_圆=π×1^2=π平方厘米。
- 那么两个圆的面积S_两个圆=2π平方厘米,取π = 3.14,则S_两个圆=2×3.14 = 6.28平方厘米。
3. 接着计算两个圆重叠部分的面积- 两个半径为1厘米的圆重叠部分是一个类似橄榄形的图形。
我们可以先算出两个扇形(圆心角为90^∘,因为圆与长方形边相切)的面积之和,再减去中间正方形的面积。
- 一个扇形的面积是圆面积的(1)/(4),所以一个扇形面积S_扇形=(1)/(4)×π×1^2=(π)/(4)平方厘米。
- 两个扇形面积S_两个扇形=(π)/(2)平方厘米,取π = 3.14,则S_两个扇形=1.57平方厘米。
- 中间正方形的面积S_正方形=1×1 = 1平方厘米。
- 所以两圆重叠部分面积S_重叠=1.57 - 1=0.57平方厘米。
4. 最后计算阴影部分面积- 阴影部分面积S_阴影=S_长方形-S_两个圆+S_重叠- 把S_长方形=48平方厘米,S_两个圆=6.28平方厘米,S_重叠=0.57平方厘米代入可得:- S_阴影=48 - 6.28+0.57 = 42.29平方厘米。
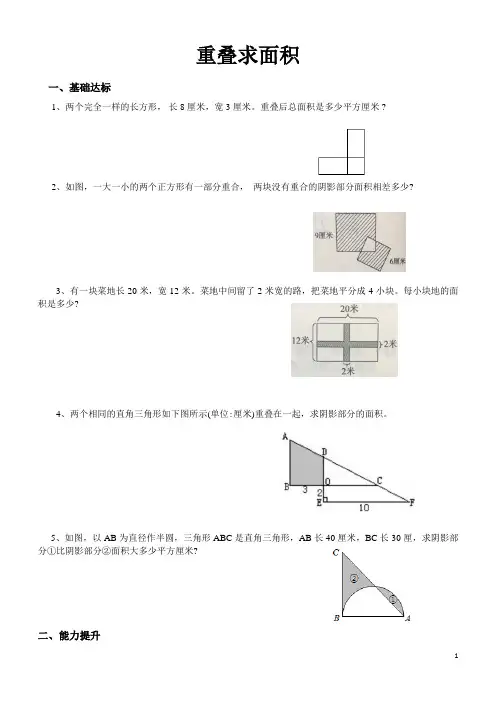
重叠求面积
一、基础达标
1、两个完全一样的长方形,长8厘米,宽3厘米。
重叠后总面积是多少平方厘米 ?
2、如图,一大一小的两个正方形有一部分重合,两块没有重合的阴影部分面积相差多少?
3、有一块菜地长20米,宽12米。
菜地中间留了2米宽的路,把菜地平分成4小块。
每小块地的面积是多少?
4、两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积。
5、如图,以AB为直径作半圆,三角形ABC是直角三角形,AB长40厘米,BC长30厘,求阴影部分①比阴影部分②面积大多少平方厘米?
二、能力提升
1、如右图,两个正方形的边长分别为14厘米和8厘米,甲、乙两块空白区域的面积之和为156平方厘米,那么阴影部分的面积是多少平方豪米。
2、如图,由两个完全一样的直角三角形叠在一起而成的,求阴影部分的面积是多少平方米?
3、如图(单位: 厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积。
4、如图,直角三角形ABC,AB长是40厘米,图中阴影部分的甲的面积比阴影部分乙的面积大148平方厘米,求:BC的长度。
5、下图的长方形是一块草坪,中同有丙条宽1米的走道,求植草的面枳。
三、竞赛链接
(第九届“走进美妙数学花园”决赛题选)如图所示,四个相叠的正方形,边长分别是11、9、7、5,求红色区与黑色区的面积差。

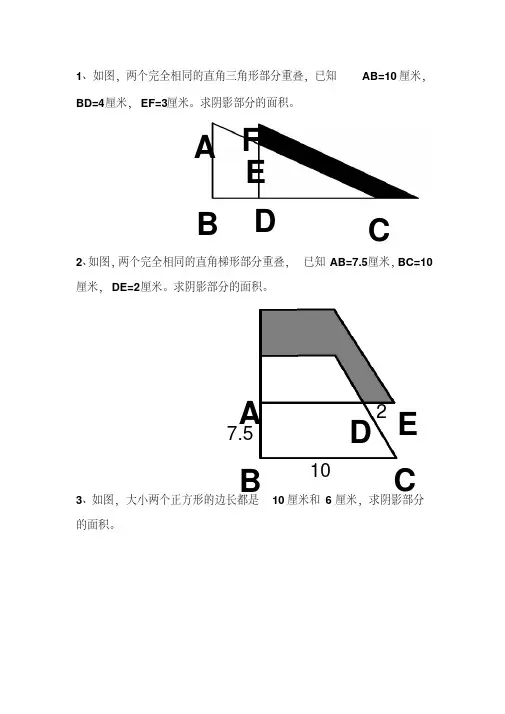
1、如图,两个完全相同的直角三角形部分重叠,已知
AB=10厘米,
BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是
10厘米和6厘米,求阴影部分的面积。
A B C
D E
F A
D
E B C
107.52
4、如图,大小两个正方形的边长都是
10厘米和6厘米,求阴影部分
的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?
A
B
C D E F
A
B C D F E G。





天开家教五年级上册组合图形面积计算过关卷求以下图形的面积:(单位: cm)47 6 4 326 8 510 85 31:一个等腰直角三角形,最长的边是10 厘米,这个三角形的面积是多少平方厘米?【稳固练习 1】:如图正方形中套着一个长方形,正方形的边长是12 厘米,长方形的四个角的极点把正方形的四条边各分红两段,此中长的一段是短的2 倍。
求中间长方形的面积。
862:求右边平行四边形的周长。
12C【稳固练习 2】:求右边三角形的AB上的高。
4 3A5 B 典型例题 3:求右图等腰直角三角形中暗影部分的面积。
(单位:厘米)104【稳固练习 3】:求四边形 ABCD的面积。
(单位:厘米)典型例题4:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是 72 平方厘米,正方形的面积分别是多少?【稳固练习4】:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是 72 平方厘米,正方形的面积分别是多少?典型例题 5:图中两个正方形的边长分别是10 厘米和 6 厘米,求暗影部分的面积。
【稳固练习 5】:图中两个正方形的边长分别是 6 厘米和 4 厘米,求暗影部分的面积。
【稳固练习 6】求右图等腰直角三角形中暗影部分的面积。
(单位:厘米)106典型例题7:在一个直角三角形铁皮上剪下一块正方形,剩下两个A三角形,已知AD=3cm,DB=4cm,两个三角形面积和是多少?C2、已知正方形 ABCD的边长是 7 厘米,求正方形 EFGH的面积。
3、求以下图长方形ABCD的面积(单位:厘米)。
4、如图,用 48m长的篱笆靠墙围了一个梯形养鸡场,求养鸡场的面积?5、在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已DB20m墙A【典型例题】【例 1】已知平行四边表的面积是28 平方厘米,【练一练】假如用铁丝围成以以下图同样的求暗影部分的面积。
平行四边形,需要用多少厘米铁丝?(单位:厘米)【例 2】以下图中甲和乙都是正方形,求暗影部分的面积。
六年级数学组合图形的面积试题答案及解析1.两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为,右下角的阴影部分(线状)面积为,求大正方形的面积.【答案】19【解析】块状部分与线状部分之间的部分称为D,则D与前者共14个方格,与后者共17个方格,因此每个方格的面积是大正方形的面积为.2.把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【答案】200【解析】图1中阴影部分占整个三角形面积的,图2中阴影部分占整个三角形面积的,故图2中阴影部分的面积为294÷=200(平方分米).3.求下列各个格点多边形的面积.【答案】15,20,14,17【解析】⑴∵;,∴(面积单位);⑵∵;,∴(面积单位);⑶∵;,∴(面积单位);⑷∵;,∴(面积单位).4.如图,每一个小方格的面积都是1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【答案】6.5【解析】方法一:正方形格点阵中多边形面积公式:(N+-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=4,L=7,则用粗线围成图形的面积为:(4+-1)×1=6.5(平方厘米)方法二:如右上图,先求出粗实线外格点内的图形的面积,有①=3÷2=1.5,②=2÷2=1,③=2÷2=1,④=2÷2=1,⑤=2÷2=l,⑥=2÷2=1,还有三个小正方形,所以粗实线外格点内的图形面积为1.5+l+1+1+1+1+3=9.5,而整个格点阵所围成的图形的面积为16,所以粗线围成的图形的面积为:16-9.5=6.5平方厘米.5.四个面积为的正六边形如图摆放,求阴影三角形的面积.【答案】13/6【解析】如图,将原图扩展成一个大正三角形,则与都是正三角形.假设正六边形的边长为为,则与的边长都是,所以大正三角形的边长为,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为,三角形的面积为.由于,,所以与三角形的面积之比为.同理可知、与三角形的面积之比都为,所以的面积占三角形面积的,所以的面积的面积为.6.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少?【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.7.如右图,过平行四边形内的一点作边的平行线、,若的面积为8平方分米,求平行四边形的面积比平行四边形的面积大多少平方分米?【答案】16【解析】根据差不变原理,要求平行四边形的面积与平行四边形的面积差,相当于求平行四边形的面积与平行四边形的面积差.如右上图,连接、.由于,所以.而,,所以(平方分米).8.右图中,和是两个正方形,和相交于,已知等于的三分之一,三角形的面积等于6平方厘米,求五边形的面积.【答案】49.5【解析】连接、,由于与平行,可知四边形构成一个梯形.由于面积为6平方厘米,且等于的三分之一,所以等于的,根据梯形蝴蝶定理或相似三角形性质,可知的面积为12平方厘米,的面积为6平方厘米,的面积为3平方厘米.那么正方形的面积为平方厘米,所以其边长为6厘米.又的面积为平方厘米,所以(厘米),即正方形的边长为3厘米.那么,五边形的面积为:(平方厘米).9.正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影面积为多少平方厘米?【答案】50【解析】方法一:三角形BEF的面积,梯形EFDC的面积三角形BEF的面积,而四边形CEFH是它们的公共部分,所以,三角形DHF的面积三角形BCH的面积,进而可得,阴影面积三角形BDF的面积三角形BCD 的面积(平方厘米).方法二:连接CF,那么CF平行BD ,所以,阴影面积三角形BDF的面积三角形BCD的面积(平方厘米).10.如右图所示,在长方形内画出一些直线,已知边上有三块面积分别是,,.那么图中阴影部分的面积是多少?【答案】97【解析】三角形的面积三角形的面积长方形面积阴影部分面积;又因为三角形的面积三角形的面积长方形面积,所以可得:阴影部分面积.11.如图,长方形的面积是2平方厘米,,是的中点.阴影部分的面积是多少平方厘米?【答案】平方厘米【解析】如下图,连接,、的面积相等,设为平方厘米;、的面积相等,设为平方厘米,那么的面积为平方厘米.,.所以有.比较②、①式,②式左边比①式左边多,②式右边比①式右边大0.5,有,即,.而阴影部分面积为平方厘米.12.如图,已知,,,,线段将图形分成两部分,左边部分面积是38,右边部分面积是65,求三角形的面积.【答案】40【解析】连接,.根据题意可知,;;所以,,,,,于是:;;可得.故三角形的面积是40.13.如图,如果长方形的面积是平方厘米,那么四边形的面积是多少平方厘米?【答案】32.5【解析】如图,过、、、分别作长方形的各边的平行线.易知交成中间的阴影正方形的边长为厘米,面积等于平方厘米.设、、、的面积之和为,四边形的面积等于,则,解得(平方厘米).14.如图,已知是梯形,∥,,,,求的面积.【答案】6【解析】本题是09年六年级试题,初看之下,是梯形这个条件似乎可以用到梯形蝴蝶定理,四边形内似乎也可以用到蝴蝶定理,然而经过试验可以发现这几个模型在这里都用不上,因为、这两个点的位置不明确.再看题目中的条件,,,这两个条件中的前一个可以根据差不变原理转化成与的面积差,则是与的面积差,两者都涉及到、以及有同一条底边的两个三角形,于是想到过、分别作梯形底边的平行线.如右图,分别过、作梯形底边的平行线,假设这两条直线之间的距离为.再过作的垂线.由于,所以,故.根据差不变原理,这个差等于与的面积之差.而与有一条公共的底边,两个三角形边上的高相差为,所以它们的面积差为,故.再看,它的面积等于是与的面积之差,这两个三角形也有一条公共的底边,边上的高也相差,所以这两个三角形的面积之差为,故.由于,所以,则,所以.15.长方形的面积为36,、、为各边中点,为边上任意一点,问阴影部分面积是多少?【答案】13.5【解析】解法一:寻找可利用的条件,连接、,如下图:可得:、、,而即;而,.所以阴影部分的面积是:解法二:特殊点法.找的特殊点,把点与点重合,那么图形就可变成右图:这样阴影部分的面积就是的面积,根据鸟头定理,则有:.16.一个长方形分成4个不同的三角形,绿色三角形面积占长方形面积的,黄色三角形面积是.问:长方形的面积是多少平方厘米?【答案】60【解析】黄色三角形与绿色三角形的底相等都等于长方形的长,高相加为长方形的宽,所以黄色三角形与绿色三角形的面积和为长方形面积的,而绿色三角形面积占长方形面积的,所以黄色三角形面积占长方形面积的.已知黄色三角形面积是,所以长方形面积等于().17.如右图,过平行四边形内的一点作边的平行线、,若的面积为8平方分米,求平行四边形的面积比平行四边形的面积大多少平方分米?【答案】16【解析】根据差不变原理,要求平行四边形的面积与平行四边形的面积差,相当于求平行四边形的面积与平行四边形的面积差.如右上图,连接、.由于,所以.而,,所以(平方分米).18.如右图,正方形的面积是,正三角形的面积是,求阴影的面积.【答案】2【解析】连接交于点,并连接.如右上图所示,可得,所以与面积相等(同底等高),所以有:,因为,所以.19.如图所示,正方形的边长为厘米,长方形的长为厘米,那么长方形的宽为几厘米?【答案】6.4【解析】本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半.证明:连接.(我们通过把这两个长方形和正方形联系在一起).∵在正方形中,边上的高,∴(三角形面积等于与它等底等高的平行四边形面积的一半)同理,.∴正方形与长方形面积相等.长方形的宽(厘米).20.如右图,在平行四边形中,直线交于,交延长线于,若,求的面积.【答案】1【解析】本题主要是让学生并会运用等底等高的两个三角形面积相等(或夹在一组平行线之间的三角形面积相等)和等量代换的思想.连接.∵∥,∴同理∥,∴又,,∴,即.。
一、引言在数学领域,求两个形状的重叠部分的面积是一项常见而又有趣的问题。
尤其是对于三年级的学生来说,通过求解两个正方形的重叠部分面积,可以锻炼他们的逻辑思维和几何空间想象能力。
本文将围绕着这个主题展开深入讨论,首先从简单的概念出发,逐步深入,帮助读者全面理解和掌握这一问题。
二、两个正方形的重叠部分面积概念解析在讨论两个正方形的重叠部分面积之前,首先需要了解正方形的特征和性质。
正方形是一种特殊的四边形,具有四条边长度相等,四个内角均为直角的特点。
当两个正方形重叠时,它们的部分区域形成了一个新的图形,我们的目标就是求解这个重叠部分的面积。
三、简单情形下的解决方法针对三年级的学生,可以从简单的情形开始引导他们理解。
通过绘制两个重叠的正方形,让学生先观察并估算重叠部分的面积。
引导他们从边长和面积的角度出发,逐步引入坐标系和矩阵的思想,帮助他们建立起解决问题的数学模型。
四、逐步深入的解决方法在学生掌握了基本概念后,可以引导他们逐步深入地思考。
可以通过平移、旋转和镜像等操作,将两个正方形重叠部分的面积问题拓展到更加复杂的情形。
这样的拓展不仅可以锻炼学生的空间想象能力,也可以让他们更好地理解数学中的抽象概念。
五、总结回顾经过以上的讨论和思考,我们不难发现,求解两个正方形重叠部分的面积并不是一项孤立的数学问题,而是需要将几何形状与数学空间结合起来进行综合思考和分析的活动。
通过这样的学习过程,学生不仅可以掌握具体的计算方法,更重要的是培养他们的逻辑思维能力和动手实践能力。
个人观点和理解作为一个数学爱好者,我认为数学不仅是一门工具性学科,更是一门富有创造性和探索精神的学科。
通过引导学生解决类似两个正方形重叠部分面积的问题,可以培养他们的数学兴趣和求知欲,激发他们对数学的热爱。
虽然这个问题看似简单,但背后却蕴含着深刻的数学内涵,希望能够引起更多学生对数学的兴趣和好奇心。
在知识的文章格式中,我们可以使用序号标注的方式对文章进行排版,以便读者更好地理解和消化文章内容。
重叠图求周长和面积的方法
要计算重叠图的周长和面积,需要知道重叠图的形状和尺寸。
以下是一些常见的方法:
1. 方形重叠图:如果重叠图是方形的,只需要知道一个边的长度即可。
周长等于4倍边长,面积等于边长的平方。
2. 矩形重叠图:如果重叠图是矩形的,需要知道两个相邻边的长度。
周长等于两个相邻边的长度之和乘以2,面积等于两个相邻边的长度之积。
3. 圆形重叠图:如果重叠图是圆形的,需要知道圆的半径。
周长等于2π乘以半径,面积等于π乘以半径的平方。
对于其他更复杂的形状的重叠图,可能需要使用数值方法、数学公式或计算机模拟来求解。
长方形与梯形重叠,求面积关系
当长方形与梯形重叠时,它们的面积关系取决于重叠部分的形状和大小。
我们可以通过以下几种情况来讨论:
1. 长方形完全包含梯形,这种情况下,重叠部分的面积就是梯形的全面积。
2. 梯形完全包含长方形,同样地,这种情况下,重叠部分的面积就是长方形的全面积。
3. 长方形与梯形部分重叠,在这种情况下,我们需要计算重叠部分的面积。
首先,我们可以找到重叠部分的四个顶点,然后计算出这四个顶点所围成的区域的面积。
这可以通过将重叠部分分割成两个三角形和一个矩形来实现,然后分别计算它们的面积,并将它们相加。
总的来说,长方形与梯形的面积关系是多种多样的,取决于它们之间的相对位置和大小关系。
在实际问题中,我们需要具体的数值或者图形才能得出具体的面积关系。
正方体重叠表面积计算
要计算正方体重叠部分的表面积,我们首先需要知道正方体的边长。
设正方体的边长为a。
正方体的表面积由六个面组成,每个面的面积都是a^2。
所以正方体的总表面积为6a^2。
当两个正方体重叠时,它们共享一部分面积。
这部分面积由两个重叠面的面积之和减去重叠部分的面积得到。
假设两个正方体的重叠面为矩形,其中一个矩形的长为x,宽为y。
那么这个矩形的面积为xy。
为了计算重叠部分的面积,我们需要确定x和y的值。
这取决于两个正方体的位置和重叠程度。
如果两个正方体完全重叠,那么重叠部分的面积就是一个正方体的表面积,即6a^2。
如果两个正方体部分重叠,我们可以通过计算矩形的长和宽来
确定重叠部分的面积。
假设两个正方体的重叠面上的一条边长为b,那么矩形的长和
宽可以分别表示为x = a b 和 y = a b。
因此,重叠部分的面积为xy = (a b)(a b) = a^2 2ab + b^2。
最后,我们可以计算出正方体重叠部分的表面积,即总表面积
减去重叠部分的面积:
重叠部分的表面积 = 6a^2 (a^2 2ab + b^2) = 5a^2 + 2ab
b^2。
以上是计算正方体重叠部分表面积的方法。
请注意,具体的数
值取决于正方体的边长和重叠程度。
有关图形重叠部分面积的计算合作探究一1:如图1,己知矩形ABCD中,AB=8,BC=4,则阴影部分的面积是多少?图1 图2例2:如图2,点A、B、C在直径为2的⊙O上,∠BAC=45°,则图中阴影部分的面积等于____结论1:利用_____来计算重叠部分的面积练一练1.如图3,在□ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是________2. .如图4将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一条直线上.若∠BCA=90°,∠BAC=30°,AB=4 cm,则图中阴影部分面积为 cm2图3 图4图5合作探究二.如图5己知直经AB=10,点C、D是圆的三等分点,求阴影部分的面积。
结论2根据平行线间的距离______,再利用 __________的三角形面积相等进行转化求值。
1如图6,A是半径为1的⊙O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于图6 图7 图8合作探究三如图7,⊙P内含于⊙O,⊙O的弦AB切⊙P于点C,且AB∥OP.若弦AB长为6,则阴影部分的面积为结论3利用____来计算重叠部分的面积1如图8,两圆内切,大半圆弦AB切小半圆于D,AB=6,则阴影部分的面积_____合作探究四:如图9,三个圆是同心圆,则图中阴影部分的面积等于_______结论3利用_____来求重叠部分的面积。
图9 图10 图111如图10,正方形的四个顶点在直径为4的大圆圆周上,四条边与小圆都相切,AB、CD过圆心O,且AB⊥CD,则图中阴影部分的面积是_______学以致用 1、如图11,扇形OAB中,∠AOB=60°AD=1,弧CD的长为,则图中阴影部分的面积为_______2.如图12在Rt△ABC中,∠C为直角,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为_________3.如图13,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BDOC=1,试求阴影部分的面积图12 图13 图144.如图14,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是(5.如图15,在△ABC中,AB=AC=2.∠ABC=30°,以A为圆心,AB为半径作弧BEC,以BC为直径作半圆,求阴影部分的面积。