下载文档原格式
将军饮马模型解答题1.问题背景:如图()a ,点B A 、在直线l 的同侧,要在直线l 上找一点C ,使AC 与BC 的距离之和最小,我们可以作出点B 关于l 的对称点B ',连接B A '与直线l 交于点C ,则点C 即为所求.（1）实践运用：如图()b ,已知,⊙O 的直径CD 为4,点A 在⊙O 上,︒=∠30ACD ,B 为弧AD 的中点,P 为直径CD 上一动点,则AP BP +的最小值为（2）知识拓展：如图()c ,在ABC Rt ∆中,10=AB ,︒=∠45BAC ,BAC ∠的平分线交BC 于点F E D 、、分别是线段AD 和AB 上的动点,求EF BE +的最小值,并写出解答过程.2.如图已知GH EF //，EF AC ⊥于点C ，EF BD ⊥于点D 交HG 于点K ．3=AC ，2=DK ，4=BK ．()1若6=CD ，点M 是CD 上一点，当点M 到点A 和点B 的距离相等时，求CM 的长； ()2若213=CD ，点P 是HG 上一点，点Q 是EF 上一点，连接QB PQ AP ,,，求QB PQ AP ++的最小值．3.边作等边BDE ∆，连接AD ，CD ．（1）求证：ADE CDB ∆≅∆；（2）若BC AC 边上找一点H ，使得BH EH +最小，并求出这个最小值．4.如图，将一副直角三角板拼放在一起得到四边形ABCD ，其中︒=∠45BAC ，︒=∠30ACD ，点E 为CD 边上的中点，连接AE ，将ADE ∆沿AE 所在直线翻折得到E AD '∆，E D '交AC 于F 点．若cm AB 26=．（1）AE 的长为 cm ；（2）试在线段AC 上确定一点P ，使得EP DP +的值最小，并求出这个最小值；（3）求点'D 到BC 的距离．5.如图,在正方形ABCD 中,点E ,F 分别是边AD ,BC 的中点,连接DF ,过点E 作DF EH ⊥,垂足为H ,EH 的延长线交DC 于点G .（1）猜想DG 与CF 的数量关系,并证明你的结论；（2）过点H 作CD MN //,分别交AD ,BC 于点M ,N ,若正方形ABCD 的边长为10,点P 是MN 上一点,求PDC ∆周长的最小值.6.且2==DE BF ．连接AE ，AF ，CE ，CF ．（1）求证：四边形AECF 是菱形；（2）求四边形AECF 的面积；（3）如果M 为AF 的中点，P 为线段EF 上的一动点，求PM PA +的最小值．7.已知菱形OBCD 在平面直角坐标系中位置如图所示，点B 的坐标为)0,2(，︒=∠60DOB .（1）点D 的坐标为 ，点C 的坐标为 ；（2）若点P 是对角线OC 上一动点，点)3,0(-E ，求PB PE +的最小值．8.如图,在平面直角坐标系xoy 中,已知直线的解析式为，直线交轴于点，交轴于点.(1)若一个等腰直角三角形的顶点与点重合，直角顶点在第一象限内，请直接写出点的坐标；(2)过点作轴的垂线，在上是否存在一点，使得的周长最小?若存在，请求出点的坐标；若不存在，请说明理由.AC 22.1+-=x y AC x C y A OBD D C B B x l l P AOP ∆P9.在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点B A 、分别在，x 轴、y 轴的正半轴上，()03，A ，()40，B ，D 为边OB 的中点. （1）若E 为边OA 上的一个动点，求△CDE 的周长最小值；（2）若F E 、为边OA 上的两个动点，且1=EF ，当四边形CDEF 的周长最小时，求点F E 、的坐标.10.如图，在矩形OABC 中，已知A ，C 两点的坐标分别为()0,4A ,()2,0C ，D 为OA 的中点．设点P 是AOC ∠平分线上的一个动点（不与点O 重合）．（1）试证明：无论点P 运动到何处，PC 总与PD 相等；（2）当点P 运动到与点B 的距离最小时，求P 的坐标；（3）已知()1,1-E ，当点P 运动到何处时，PDE ∆的周长最小？求出此时点P 的坐标和PDE ∆的周长．11.一次函数b kx y +=的图象与x 、y 轴分别交于点()0,2A ()4,0B ,O 为坐标原点，线段AB OA ，的中点分别为点P D C ,,为直线OB 上一动点．（1）当点P 在直线OB 上运动时，PCD △的面积是否发生变化？请说明理由；（2）当点P 在直线OB 上运动时，PCD △的周长是否发生变化？如果发生变化，求出PCD △的最小周长及周长最小时P 点的坐标；（3）直接写出PCD △为等腰三角形时P 点的坐标；（4）直接写出PCD △为直角三角形时P 点的坐标．12.一次函数2521+-=x y 的图象与反比例函数)0(＞k xk y =的图象交于B A 、两点，过点A 作x 轴的垂线，垂足为M ，AOM ∆面积为1.（1）求反比例函数的解析式；（2）在y 轴上求一点P ，使PB PA +的值最小，并求出其最小值和P 点坐标.13.如图，正方形AOCB 在平面直角坐标系xoy 中，点O 为原点，点B 在反比例函数)0(＞x xk y =图象上，BOC ∆的面积为8．（1）求反比例函数的关系式；（2）若动点E 从A 开始沿AB 向B 以每秒1个单位的速度运动，同时动点F 从B 开始沿BC 向C 以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t 表示，BEF ∆的面积用S 表示，求出S 关于t 的函数关系式；（3）当运动时间为34秒时，在坐标轴上是否存在点P ，使PEF ∆的周长最小？若存在，请求出点P 的坐标；若不存在，请说明理由．14．已知在中边的长与的长与边上的高的和为．试：（1）写出的面积与的长之间的函数解析式及自变量的取值范围；（2）当时求边上的高及此时三角形的面积；（3）当面积为（2）所求结果时，是否存在其周长最小的情形？如果存在，请求出其最小周长，如果不存在请说明理由．15.如图，抛物线522++=bx ax y 经过)0,1(-A ,)0,5(B 两点. （1）求抛物线的解析式，并直接写出抛物线的顶点坐标；（2）在抛物线的对称轴上有一点P ，使PC PA +的值最小，求点P 的坐标；（3）点M 为x 轴上一动点，在抛物线上是否存在一点N ，使以A ，C ，M ，N 四点构成的四边形为平行四边形？若存在，请直接写出N 点的坐标；若不存在，请说明理由.16.如图,直线b kx y +=交x 轴于点()0,1-A ,交y 轴于点()4,0B ,过A ,B 两点的抛物线交x 轴于另一点C .（1）直线的解析式为___________；（2）该抛物线对称轴上有一动点P ,连接PA ,PB ,若PB PA +最小值为5,求此时抛物线的解析式以及点P 坐标；（3）在（2）的条件下,在抛物线对称轴上是否存在点Q ,使ABQ ∆是等腰三角形?若存在,求出符合条件的Q 点坐标；若不存在,请说明理由.ABC ∆BC BC BC 20ABC ∆y BC x x 10=BCBC17.如图,已知抛物线()02≠++=a c bx ax y 的对称轴为1-=x ，且抛物线经过)0,1(A ,)3,0(C 两点，与x 轴交于点B .(1)求抛物线的解析式；(2)在抛物线的对称轴1-=x 上找一点M ，使点M 到点A 的距离与到点C 的距离之和最小，求此时点M 的坐标；(3)设点P 为抛物线对称轴1-=x 上的一个动点，求使BPC ∆为直角三角形的点P 的坐标.18.如图,以D 为顶点的抛物线c bx x y ++-=2交x 轴于B A 、两点,交y 轴于点C ,直线BC 的表达式为3+-=x y .（1）求抛物线的表达式；（2）在直线BC 上有一点P ,使PA PO +的值最小,求点P 的坐标；（3）在x 轴上是否存在一点Q ,使得以Q C A 、、为顶点的三角形与△BCD 相似?若存在,请求出点Q 的坐标；若不存在,请说明理由.19.如图，抛物线）（042≠-+=a bx ax y 与x 轴交于)0,4(A )0,1(-B 两点，过点A 的直线4+-=x y 交抛物线于点C ．（1）求此抛物线的解析式；（2）在直线AC 上有一动点E ，当点E 在某个位置时，使BDE △的周长最小，求此时E 点坐标；（3）当动点E 在直线AC 与抛物线围成的封闭线A D B C A →→→→上运动时，是否存在使BDE △为直角三角形的情况，若存在，请直接写出符合要求的E 点的坐标；若不存在，请说明理由．20．如图，已知抛物线83212-+=x x y 的图象与x 轴交于A ，B 两点（点A 在点B 的右侧），与y 轴交于点C ．（1）求直线BC 的解析式；（2）点F 是直线BC 下方抛物线上的一点，当BCF △的面积最大时，在抛物线的对称轴上找一点P ，使得BFP △的周长最小，请求出点F 的坐标和点P 的坐标；（3）在（2）的条件下，是否存在这样的点),0(m Q ，使得BFQ △为等腰三角形？如果有，请直接写出点Q 的坐标；如果没有，请说明理由．21.如图，直线343+=x y 分别与x 轴， y 轴交于点A ， B ，抛物线122++-=x x y 与y 轴交于点C ． 若点E 在抛物线122++-=x x y 的对称轴上移动，点F 在直线AB 上移动，求EF CE +的最小值．22.如图，已知抛物线经过点）（3,2-B ，原点O 和x 轴上一点另一点A ，它的对称轴与x 轴交于点）（0,2C .（1）求此抛物线的函数解析式（2）连接CB ，在抛物线的对称轴上找一点E ，使得CE CB =，求点E 的坐标（3）在（2）的条件下，连接BE ，设BE 的中点为G ，在抛物线的对称轴上是否存在一点P ，使得PBG △的周长最小，若存在，求出点P 的坐标，若不存在，请说明理由.23.如图，在平面直角坐标系中，一次函数432+-=x y 的图像与x 轴和y 轴分别相交于B A 、两点．动点P 从点A 出发，在线段AO 上以每秒3个单位长度的速度向点O 作匀速运动，到达点O 停止运动．点A 关于点P 的对称点为点Q ，以线段PQ 为边向上作正方形PQMN ．设运动时间为t 秒．（1）当31t =秒时，点Q 的坐标是______； （2）在运动过程中，设正方形PQMN 与△AOB 重叠部分的面积为S ，求S 与t 的函数表达式；（3）若正方形PQMN 对角线的交点为T ，请直接写出在运动过程中PT OT +最小值．24.如图，矩形ABCD 中，6AB cm =，8BC cm =，动点E 从点A 出发，沿AC 向点C 运动，速度为1/cm s ，点E 到达点C 时停止运动，连接DE 并延长交矩形ABCD 的边于点F ．点M 与点C 重合，MN DF ⊥于点H 交矩形的边AD 于点N ．设点E 运动的时间为()t s ．（1）当点F 到达点B 时，求t 的值；（2）当2t =时，求ND 的长；（3）如图2，点M 从点C 开始沿CD 边向点D 运动，速度为1/cm s ，且与点E 同时开始运动，当点M 停止运动时，点E 也停止运动，其他条件不变．①连接FM ，点Q 为FM 的中点，点P 在CD 边上，4CP cm =，请直接写出点F 从点A 运动到点B 的过程中，PQC ∆周长的最小值；②当13EF ED =时，请直接写出线段ND 的长．25.如图，(2,0)B -，(0,4)C ，将BOC ∆绕原点O 顺时针旋转90︒得到DOA ∆，抛物线24y ax bx =++经过A ，B 两点．（1）求抛物线的解析式；（2）将ADO ∆以秒一个单位的速度沿x 轴向左平移，平移后的三角形记为△D O A '''，平移时间为t 秒．①当D '落在抛物线上时，求t 的值；②连接A C '，当t 为何值时，△D A C '''的周长最小？直接写出t 的值和△D A C '''周长的最小值．26．如图①，已知抛物线c bx ax y ++=2的图象经过点)3,0(A 、)0,1(B ，其对称轴为直线l ：2=x ，过点A 作x AC ∥轴交抛物线于点C ，AOB ∠的平分线交线段AC 于点E ，点P 是抛物线上的一个动点，设其横坐标为m ．（1）若动点P 在直线OE 下方的抛物线上，连结PE 、PO ，当m 为何值时，四边形AOPE 面积最大？当四边形AOPE 面积最大时，在抛物线对称轴直线上找一点M ，使得MP MB -的值最大，并求出这个最大值．（2）如图②，F 是抛物线的对称轴l 上的一点，在抛物线上是否存在点P 使POF △成为以点P 为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P 的坐标；若不存在，请说明理由．27.阅读材料：“最值问题”是数学中的一类较具挑战性的问题．其实，数学史上也有不少相关的故事，如下即为其中较为经典的一则：海伦是古希腊精通数学、物理的学者，相传有位将军曾向他请教一个问题﹣﹣如图①，从A 点出发，到笔直的河岸l 去饮马，然后再去B 地，走什么样的路线最短呢？海伦轻松地给出了答案：作点A 关于直线l 的对称点'A ，连结B A '交l 于点P ，则B A PB PA '=+的值最小．解答问题：（1）如图，已知菱形ABCD 的边长为12， 60=∠DAB ．点P 为AC 线段上一动点，点E 为AD 线段上一动点，求线段PE DP +的最小值．（2）如图，已知菱形ABCD 的边长为12， 60=∠DAB ．将此菱形放置于平面直角坐标系中，各顶点恰好在坐标轴上．现有一动点P 从点A 出发，以每秒2个单位的速度，沿A →C 的方向，向点C 运动．当到达点C 后，立即以相同的速度返回，返回途中，当运动到x 轴上某一点M 时，立即以每秒1个单位的速度，沿M →B 的方向，向点B 运动．当到达点B 时，整个运动停止． ①为使点P 能在最短的时间内到达点B 处，试确定点M 的位置，并说明理由．②在①的条件下，设点P 的运动时间为)(s t ，PAB ∆的面积为S ，在整个运动过程中，试求S 与t 之间的函数关系式，并指出自变量t 的取值范围．28．（1）如图1，OC 平分AOB ∠，点D 是射线OA 边上一点，点P 、Q 分别在射线OC 、OB 上运动，已知10=OD ，︒=∠30AOC ，则PQ DP +的最小值是 ；（2）如图2，在菱形ABCD 中，8=AB ，︒=∠60DAB ，点E 是AB 边上的动点，点F 是对角线AC 上的动点，求BF EF +的最小值；（3）如图3，在矩形ABCD 中，8=AB ，4=AD ，点M 是AB 上一动点，点N 是对角线AC 上一动点，请直接写出BN MN +的最小值．29.【探究问题】正的边长为，是它的高线．（1）如图（1），点、分别是正的边和高上的两个动点，求BQ +QP 的最小值；（2）如图（2），点是正高上的一动点，当为何值时，最小？并ABC ∆cm 8AD P Q ABC ∆AB AD M ABC ∆AD AM MC AM +21求出这个最小值；【解决问题】如图（3），、两地相距，是一条沿东西方向向两边延伸的一条铁路．点到的最短距离为．今计划在铁路线上修一个中转站，再在间修一条笔直的公路到地．如果同样的物资在每千米公路上的运费是铁路上的两倍．那么，为使通过铁路由到再通过公路由到的总运费达到最小值，请求出的长．（结果保留根号）30.如图1，已知抛物线2y =++与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，点D 是点C 关于抛物线对称轴的对称点，连接CD ，过点D 作DH x ⊥轴于点H ，过点A 作AE AC ⊥交DH 的延长线于点E ．（1）求线段DE 的长度；（2）如图2，试在线段AE 上找一点F ，在线段DE 上找一点P ，且点M 为直线PF 上方抛物线上的一点，求当CPF ∆的周长最小时，MPF ∆面积的最大值是多少；（3）在（2）问的条件下，将得到的CFP ∆沿直线AE 平移得到△C F P '''，将△C F P '''沿C P ''翻折得到△C P F ''''，记在平移过称中，直线F P ''与x 轴交于点K ，则是否存在这样的点K ，使得△F F K '''为等腰三角形？若存在求出OK 的值；若不存在，说明理由．31.如图，将边长为6的正三角形纸片ABC 按如下顺序进行两次折叠，展开后，得折痕BE AD ，（如图①），点O 为其交点.（1）探求AO 与OD 的数量关系，并说明理由；（2）如图②，若N P ，分别为BC BE ，上的动点.①当PD PN +的长度取得最小值时，求BP 的长度；②如图③，若点Q 在线段BO 上，1=BQ ，则PD NP QN ++的最小值=.A B km 100AC B AC km 60AC M BM B A M M BAM32.已知,如图,二次函数()0322≠-+=a a ax ax y 图象的顶点为H ,与x 轴交于B A 、两点,点B H 、关于直线l :333+=x y 对称. （1）求B A 、两点坐标,并证明点A 在直线l 上；（2）求二次函数表达式；（3）过点B 作直线BK ∥AH 交直线l 于K 点,N M 、分别为直线AH 和直线l 上的两个动点,连接MK NM NH 、、,求MK NM NH ++的最小值.33.如图，抛物线44y 2+-=x x 与y 轴交于点A ，B 是OA 的中点．一个动点G 从点B 出发，先经过x 轴上的点M ，再经过抛物线对称轴上的点N ，然后返回到点A ．如果动点G 走过的路程最短，请找出点M 、N 的位置，并求最短路程．34.如图1,抛物线)0(y 2≠++=a c bx ax 的顶点为)4,1(C ,交x 轴于B A 、两点,交y 轴于点D ,其中点的坐标B 为()0,3.(1)求抛物线的解析式；(2)如图2，过点A 的直线与抛物线交于点E ，交y 轴于点F ，其中点E 的横坐标为2，若直线PQ 为抛物线的对称轴，点G 为直线PQ 上的一动点，则X 轴上是否存在一点F H G D 、、、，使四点所围成的四边形周长最小?若存在，求出这个最小值及点H G 、的坐标；若不存在，请说明理由.35.如图，甲、乙两个单位分别位于一条封闭式街道的两旁，现准备合作修建一座过街天桥．问：（1）桥建在何处才能使由甲到乙的路线最短？（注：桥必须与街道垂直）．（2）桥建在何处才能使甲、乙到桥的距离相等？36.如图,二次函数x x y 42-=的图象与x 轴,直线y ＝x 的一个交点分别为点A .B ,CD 是线段OB 上的一动线段,且22=CD ,过点C .D 的两直线都平行于y 轴,与抛物线相交于点F ,E ，连接EF .（1）点A 的坐标为 ,线段OB 的长= ；（2）设点C 的横坐标为m ,①当四边形CDEF 是平行四边形时，求m 的值；②连接AC .AD ,求m 为何值时，△ACD 的周长最小，并求出这个最小值．37.已知平面直角坐标系中，A B 、两点的坐标分别为)3,2(-、)1,4(-.（1）若0P x （，）是x 轴上的一个动点，当PAB △的周长最短时，求x 的值； （2）若030C a D a +（，），（，）是x 轴上的两个动点，当四边形ABDC 的周长最短时，求a 的值．38.已知点()4,3A ，点B 为直线1-=x 上的动点，设()y B ,1．（1）如图1，若点()0，x C 且31＜＜x -，AC BC ⊥，求y 与x 之间的函数关系式； （2）在（1）的条件下，y 是否有最大值？若有，请求出最大值；若没有，请说明理由；（3）如图2，当点B 的坐标为)1,1(-时，在x 轴上另取两点F E ,，且1=EF ．线段EF 在x 轴上平移，线段EF 平移至何处时，四边形ABEF 的周长最小？求出此时点E 的坐标．40.如图，平面直角坐标系中，直线83+=x y 分别交x 轴，y 轴于B A ,两点，点C 为OB 的中点，点D 在第二象限，且四边形AOCD 为矩形．(1)直接写出点B A ,的坐标，并求直线AB 与CD 交点E 的坐标；(2)动点P 从点C 出发，沿线段CD 以每秒1个单位长度的速度向终点D 运动；同时，动点N 从点A 出发，沿射线AO 以每秒2个单位长度的速度运动，当点C 到达D 点时，两点同时停止运动．过点P 作PH OA ⊥，垂足为H ，连接NP ，设点P 的运动时间为t 秒．①是否存在NPH △的面积为4，如果存在，请说明理由；②点Q 是点B 关于点A 的对称点，问HQ PH BP ++是否有最小值?如果有，求出相应的点P 的坐标；如果没有，请说明理由．41.如图，对称轴为直线2=x 的抛物线经过)0,1(-A ，)5,0(C 两点，与x 轴另一交点为B ．已知)1,0(M ，)0,(a E ，)0,1(+a F ，点P 是第一象限内的抛物线上的动点．（1）求此抛物线的解析式；（2）当1=a 时，求四边形MEFP 的面积的最大值，并求此时点P 的坐标；（3）若PCM △是以点P 为顶点的等腰三角形，求a 为何值时，四边形PMEF 周长最小？请说明理由．42.如图1，已知抛物线1(2)()(0)y x x a a a=-+>与x 轴从左至右交于A ，B 两点，与y 轴交于点C ．（1）若抛物线过点5(1,)4T -，求抛物线的解析式；（2）在第二象限内的抛物线上是否存在点D ，使得以A 、B 、D 三点为顶点的三角形与ABC ∆相似？若存在，求a 的值；若不存在，请说明理由．（3）如图2，在（1）的条件下，点P 的坐标为(1,1)-，点(6,)Q t 是抛物线上的点，在x 轴上，从左至右有M 、N 两点，且2MN =，问MN 在x 轴上移动到何处时，四边形PQNM 的周长最小？请直接写出符合条件的点M 的坐标．43.如图，已知在平面直角坐标系xoy 中，直角梯形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，2==AB OA ，3=OC ，过点B 作BC BD ⊥，交OA 于点D ．将DBC ∠绕点B 按顺时针方向旋转，角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F ．（1）求经过A 、B 、C 三点的抛物线的解析式；（2）当BE 经过（1）中抛物线的顶点时，求CF 的长；（3）在抛物线的对称轴上取两点P 、Q （点Q 在点P 的上方），且1=PQ ，要使四边形BCPQ 的周长最小，求出P 、Q 两点的坐标．44.如图，已知点()84-，A 和点()n ,2B 在抛物线2ax y =上． (1)求a 的值及点B 关于x 轴对称点P 的坐标，并在x 轴上找一点Q ，使得QB AQ +最短，求出点Q 的坐标；(2)平移抛物线2ax y =，记平移后点A 的对应点为A '，点B 的对应点为B '，点()0,2-C 和点()0,4-D 是x 轴上的两个定点．①当抛物线向左平移到某个位置时，B C C A '+'最短，求此时抛物线的函数解析式；②当抛物线向左或向右平移时，是否存在某个位置，5使四边形CD B A ''的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．45．在平面直角坐标系中，已知点()0,2-A ，点()4,0B ，点E 在OB 上，且OBA OAE ∠=∠．（1）如图①，求点E 的坐标；（2）如图②，将AEO △沿x 轴向右平移得到'''O E A △，连接B A '、'BE ．①设m '=AA ，其中2m 0＜＜，试用含m 的式子表示22''BE B A +，并求出使22''BE B A +取得最小值时点'E 的坐标；②当''BE B A +取得最小值时，求点'E 的坐标（直接写出结果即可）．46.在菱形中,cm AB 8=,︒60=ABC ∠,点E ,F 分别是BC ,CD 上的动点（不与B ,C ,D 重合）,连接AE ,AF .（1）如图1,若CF CE =,求证：AE =AF .（2）如图2,若BC DF BE =+.①AE 与AF 是否相等？并说明理由；②四边形AECF 的面积是2cm .（3）点E 从点B 出发以每秒3cm 的速度沿BC 方向向点C 匀速运动,同时点F 从点D出发以每ABCD秒cm 2的速度沿DC 方向向点C 匀速运动,当其中一点到达终点时另一个点也随之停止运动,又知点P 是ABC ∠平分线上一点,连接EP ,FP ,当FP EP +的值最小时,CE 的长是cm .47.如图,在平面直角坐标系中,抛物线234322+--=x x y 与x 轴交于C B 、两点,与y 轴交于点A ,抛物线的顶点为D .(1)填空:点A 的坐标为；点B 的坐标为；点D 的坐标为；(2)点P 是线段BC 上的动点（点P 不与点C B 、重合）.①过点P 作x 轴的垂线交抛物线于点E ,若PC PE =,求点E 的坐标；②在①的条件下,点F 是坐标轴上的点,且点F 到EA 和ED 的距离相等,请直接写出线段EF 的长；③若点Q 是线段AB 上的动点（点Q 不与点B A 、重合）,点R 是线段AC 上的动点（点R 不与点C A 、重合）,请直接写出PQR △周长的最小值.48.如图，锐角中，，，的面积为．（）若点在边上且，，分别为边，上的动点．求PDE △周长的最小值；（）假设一只小羊在区域内，从路边某点出发跑到水沟边喝水，然后跑向路边吃草，再跑回出发点处休息，直接写出小羊所跑的最短路程．ABC ∆︒=∠30ACB 5=AB ABC ∆231P AB 103=CP D E AC BC 2ABC ∆AB AC BC49.如图,在直角坐标系中,已知点()10，A ,()44-，B 将点B 绕点A 顺时针方向旋转︒90到点C ,顶点在坐标原点的拋物线经过点B .(1)求抛物线的解析式和点C 的坐标；(2)抛物线上一动点P ,设点P 到x 轴的距离为1d ,点P 到点A 的距离为2d ,试说明112+=d d ；(3) 在(2)的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出的△PAC 周长的最小值50.如图1，抛物线c bx x y ++-=232，与x 轴交于点A ())0,2(,0,3-B 两点，与y 轴交于点C ，连接AC .（1）求抛物线的解析式；（2）如图2，动点Q 在第一象限的抛物线上运动，连接QO 交线段AC 于点E ，过点A 作直线y AF ∥轴，点F 在x 轴上方，且满足CE AF =.①当AEF ∆是直角三角形时，求线段AF 的长；OE 的值最小时，直接写出线段AF的长.②当OF。
2022-2023学年小学三年级思维拓展举一反三精编讲义专题09 重叠问题知识精讲专题简析：三（1）班准备给参加班级绘画比赛的16位同学和参加朗读比赛的12位同学每人发一份纪念品，当中队长玲玲将28份纪念品发下去时，却多出5份，这是怎么回事？对了，因为有5位同学既参加了绘画比赛，又参加了朗读比赛，所以奖品就多出了5份。
数学中，我们将这样的问题称为重叠问题。
解答重叠问题要用到数学中的一个重要原理——包含与排除原理，即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。
解答重叠问题的应用题，必须从条件入手进行认真的分析，有时还要画出图示，借助图形进行思考，找出哪些是重复的，重复了几次？明确求的是哪一部分，从而找出解答方法。
典例分析【典例分析01】六一儿童节，学校门口挂了一行彩旗。
小张从前数起，红旗是第8面；从后数起，红旗是第10面。
这行彩旗共多少面？【思路引导】根据题意，画出下图：8面10面面从图上可以看出，从前数起红旗是第8面，从后数起是第10面，这样红旗就数了两次，重复了一次，所以这行彩旗共有8＋10－1=17面。
【典例分析02】同学们排队做操，每行人数同样多。
小明的位置从左数起是第4个，从右数起是第3个，从前数起是第5个，从后数起是第6个。
做操的同学共有多少个？【思路引导】根据题意，画出下图：由图可看出：小明的位置从左数第4个，右数第3个，说明横行有4＋3－1=6个人；从前数第5个，从后数第6个，说明竖行有5＋6－1=10人，所以做操的同学共有：6×10=60人。
【典例分析03】 把两块一样长的木板像下图这样钉在一起成了一块木板。
如果这块钉在一起的木板长120厘米，中间重叠部分是16厘米，这两块木板各长多少厘米？【思路引导】把等长的两块木板的一端钉起来，钉在一起的长度就是重叠部分，重叠的部分是16厘米，所以这两块木板的总长度是120＋16=136厘米，每块木板的长度是136÷2=68厘米。
专题10 动点产生的面积关系教学重难点1.体会点的运动过程，能从点的运动过程中抓住一些不变的量；2.能从点的运动过程中建立自变量与面积的关系式；3.让学生学会求一些基本图形的面积；4.体会压轴题的解题方法和思路。
【备注】：1.此部分知识点梳理，根据第1个图先让学生初步体会到压轴题中求图形面积的种类，可以看看每一类图形学生都是怎么求解的；2再根据第2个图引导学生总结求三角形面积的一般方法。
时间5分钟左右完成。
压轴题中求图形面积类型：三角形面积的一般求解方法：【备注】：1.以下每题教法建议，请老师根据学生实际情况参考；2.在讲解时：不宜采用灌输的方法，应采用启发、诱导的策略，并在读题时引导学生发现一些题目中的条件（相等的量、不变的量、隐藏的量等等），使学生在复杂的背景下自己发现、领悟题目的意思；3.可以根据各题的“参考教法”引导学生逐步解题，并采用讲练结合；注意边讲解边让学生计算，加强师生之间的互动性，让学生参与到例题的分析中来；4.例题讲解，可以根据“参考教法”中的问题引导学生分析题目，边讲边让学生书写，每个问题后面有答案提示；5.引导的技巧：直接提醒，问题式引导，类比式引导等等；6.部分例题可以先让学生自己试一试，之后再结合学生做的情况讲评；7.每个题目的讲解时间根据实际情况处理，建议每题7分钟，选讲例题在时间足够的情况下讲解。
例1（2020静安区建承中学一模）在平面直角坐标系xOy 中（如图），已知二次函数2y ax bx c =++（其中a 、b 、c 是常数，且a ≠0）的图像经过点A （0，-3）、B （1，0）、C （3，0），联结AB 、AC ．（1）求这个二次函数的解析式；（2）点D 是线段AC 上的一点，联结BD ，如果:3:2ABD BCD S S ∆∆=，求tan∠DBC 的值； （3）如果点E 在该二次函数图像的对称轴上，当AC 平分∠BAE 时，求点E 的坐标．【整体分析】（1）直接利用待定系数法，把A 、B 、C 三点代入解析式，即可得到答案； （2）过点D 作DH ∠BC 于H ，在∠ABC 中，设AC 边上的高为h ，利用面积的比得到32AD DC =，然后求出DH 和BH ，即可得到答案；（3）延长AE 至x 轴，与x 轴交于点F ，先证明△OAB∠∠OFA ，求出点F 的坐标，然后求出直线AF 的方程，即可求出点E 的坐标. 【详解】解：（1）将A （0，-3）、B （1，0）、C （3，0）代入20y ax bx c a =++≠（）得，03,0934,300a b a b c =+-⎧⎪=+-⎨⎪-=++⎩解得143a b c =-⎧⎪=⎨⎪=-⎩，∴此抛物线的表达式是：243y x x =-+-．（2）过点D 作DH ⊥BC 于H ，在∠ABC中，设AC边上的高为h，则11:():():3:222ABD BCDS S AD h DC h AD DC∆∆=⋅⋅==，又∠DH//y轴，∴25 CH DC DHOC AC OA===．∵OA=OC=3，则∠ACO=45°，∴△CDH为等腰直角三角形，∴26355 CH DH==⨯=．∴64255 BH BC CH=-=-=．∴tan∠DBC=32 DHBH=.（3）延长AE至x轴，与x轴交于点F，∠OA=OC=3，∴∠OAC=∠OCA=45°，∠∠OAB=∠OAC-∠BAC=45°-∠BAC，∠OFA=∠OCA-∠FAC=45°-∠FAC，∠∠BAC=∠FAC，∴∠OAB=∠OFA ． ∴△OAB∠∠OFA ， ∴13OB OA OA OF ==． ∴OF=9，即F （9，0）；设直线AF 的解析式为y=kx+b （k≠0），可得093k b b =+⎧⎨-=⎩ ，解得133k b ⎧=⎪⎨⎪=-⎩，∴直线AF 的解析式为：133y x =-， 将x=2代入直线AF 的解析式得：73y =-，∴E （2，73-）. 【点睛】本题考查了相似三角形的判定和性质，二次函数的性质，求二次函数的解析式，等腰直角三角形的判定和性质，求一次函数的解析式，解题的关键是掌握二次函数的图像和性质，以及正确作出辅助线构造相似三角形.例2..已知9023ABC AB BC AD BC P ∠===°，，，∥，为线段BD 上的动点，点Q 在射线AB 上，且满足PQ AD PC AB =（如图所示）。
巧用图形运动妙解面积问题作者：***来源：《初中生世界·七年级》2021年第02期在求幾何图形的面积时，我们常会见到所给图形不规则，很难直接利用面积公式计算的问题。
如果对图形进行适当的变换，即利用平移、翻折、旋转，将不规则的几何图形转化为规则的几何图形，就很容易计算其面积。
一、利用平移巧算面积例1求图1中S形水泥路面的面积。
（单位：m）【分析】图中的弯路是不规则图形，无法运用公式直接求出，即使运用割补法也感觉无从下手。
由于图中弯路面的宽度都为2m，因此可以把左边甲部分向右平移2m，使S形水泥路面的两边重合，图形就转化成了下图：这时，S形水泥路面的面积就转化为了图中阴影部分的面积。
解：S水泥路=S阴=30×2=60（m2）。
答：S形水泥路面的面积是60m2。
二、运用旋转巧算面积例2如图3，最大圆的半径为5cm，求图中阴影部分的面积。
【分析】图中的三个阴影分散，不易分别算其面积，但我们可通过旋转将分散的三部分阴影集中转化为四分之一圆，即阴影的面积等于四分之一圆的面积。
解：将最小圆连同阴影绕圆心顺时针旋转90°，将最外面的大圆环连同阴影绕圆心逆时针旋转90°，则三、运用翻折巧算面积4例3如图4，在正方形ABCD中，点E是以AB为直径的半圆与对角线AC的交点，若圆的直径等于2，求图中阴影部分的面积。
【分析】图中的两个阴影分散，不易分别算其面积，但我们可通过翻折将两部分阴影的面积转化为求四分之一正方形的面积。
解：如图5所示，把正方形ABCD沿直线MN翻折，连接BE。
根据题意，得AE=BE，∠AEB=90°，答：阴影部分的面积为1。
将图形进行适当的变换，可以把分散的不规则的几何图形转化为规则的几何图形，以方便计算它们的面积。
（作者单位：江苏省兴化市戴泽初级中学）。
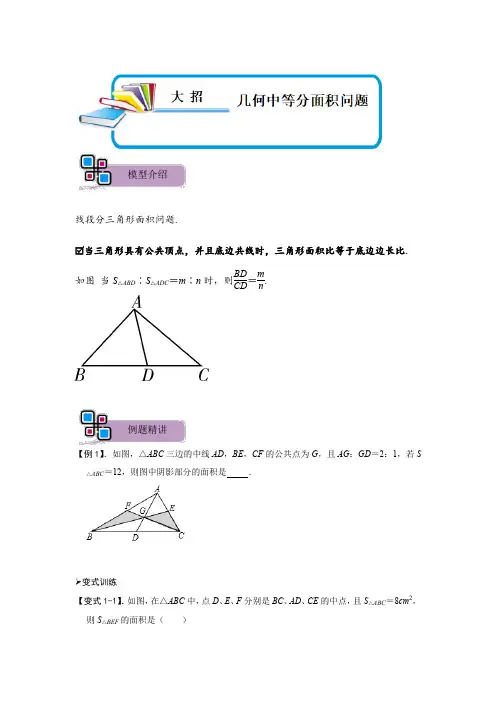
线段分三角形面积问题.当三角形具有公共顶点，并且底边共线时，三角形面积比等于底边边长比.如图 当S △ABD ∶S △ADC ＝m ∶n 时，则BD CD ＝m n .【例1】．如图，△ABC 三边的中线AD ，BE ，CF 的公共点为G ，且AG ：GD ＝2：1，若S△ABC ＝12，则图中阴影部分的面积是 ．➢变式训练【变式1-1】．如图，在△ABC 中，点D 、E 、F 分别是BC 、AD 、CE 的中点，且S △ABC ＝8cm 2，则S △BEF 的面积是（ ）模型介绍例题精讲A．4cm2B．3cm2C．2cm2D．1cm2【变式1-2】．如图，在直角坐标系中，平行四边形OABC的顶点坐标B（17，6），C（5，6），直线y＝x+b恰好将平行四边形OABC的面积分成相等的两部分，那么b＝．【例2】．如图，在平面直角坐标系xOy中，长方形OABC的顶点B的坐标为（6，4），直线y＝﹣x+b恰好将长方形OABC分成面积相等的两部分，那么b＝．➢变式训练【变式2-1】．如图，在菱形ABCD中，AB＝6，∠B＝60°，点E在边AD上，且AE＝2．若直线l经过点E，将该菱形的面积平分，并与菱形的另一边交于点F，则线段EF的长为．【变式2-2】．如图，△ABC的面积为1，D、E分别为AB、AC的中点，F、G是BC边上的三等分点．那么△DEF的面积是多少？△DOE的面积是多少？【变式2-3】．如图，在平面直角坐标系xOy中，多边形OABCDE的顶点坐标分别是O（0，0），A（0，6），B（4，6），C（4，4），D（6，4），E（6，0）．若直线l经过点M（2，3），且将多边形OABCDE分割成面积相等的两部分，求直线l 的函数表达式．1．如图，长方形ABCD的面积为36cm2，E，F，G分别为AB，BC，CD的中点，H为AD 上任一点，则图中阴影部分的面积为（）A．18cm2B．16cm2C．20cm2D．24cm22．已知梯形ABCD的四个顶点的坐标分别为A（﹣1，0），B（5，0），C（2，2），D（0，2），直线y＝kx+2将梯形分成面积相等的两部分，则k的值为（）A．B．C．D．3．如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是角平分线，CF交AD 于点G，交BE于点H．①△ABE的面积＝△BCE的面积；②AF＝FB；③∠F AG＝2∠ACF．以上说法正确的是（）A．①③B．①②C．②③D．①②③4．如图，在△ABC中，已知点D、E、F分别为BC、AD、CE的中点，若阴影部分的面积为4，则△ABC的面积为．5．如图，已知在平面直角坐标系中，平行四边形ABCD顶点A（0，0），C（10，4），直线y＝ax﹣2a﹣1将平行四边形ABCD分成面积相等的两部分，求a的值．6．如图，在平面直角坐标系中，四边形ABCO是正方形，点B的坐标为（4，4），直线y ＝mx﹣2恰好把正方形ABCO的面积分成相等的两部分，则m＝．7．已知平面上四点A（0，0），B（10，0），C（14，6），D（4，6），若直线y＝mx﹣3m﹣1将四边形ABCD分成面积相等的两部分，则m的值为．8．在△ABC中，BC＝5，AC＝12，AB＝13，在AB、AC上分别取点D、E，使线段DE将△ABC分成面积相等的两部分，则这样线段的最小值是．9．如图，在直角坐标系中，矩形OABC的顶点B的坐标为（15，6），直线恰好将矩形OABC分成面积相等的两部分，那么b＝．10．如图，△ABC中，AD是中线，延长AD到E，使DE＝AD，DF是△DCE的中线．已知△ABC的面积为2，求：△CDF的面积．11．正方形ABCD的边长为4，将此正方形置于平面直角坐标系中，使AB边落在X轴的正半轴上，且A点的坐标是（1，0）．（1）直线y＝x经过点C，且与x轴交于点E，求四边形AECD的面积；（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；（3）若直线l1经过点F（﹣，0），且与直线y＝3x平行，将（2）中直线l沿着y轴向上平移个单位交轴x于点M，交直线l1于点N，求△NMF的面积．12．如图，直线y＝2x+4与x轴、y轴分别交于A、B两点，把△OAB绕点O顺时针旋转90°得到△OCD．（1）求经过A、B、D三点的抛物线的解析式；（2）在所求的抛物线上是否存在一点P，使直线CP把△OCD分成面积相等的两部分？如果存在，求出点P的坐标；如果不存在，请说明理由．13．已知菱形OABC在坐标系中的位置如图所示，O是坐标原点，点C（1，2），点A在x 轴上．点M（0，2）．（1）点P是直线OB上的动点，求PM+PC最小值．（2）将直线y＝﹣x﹣1向上平移，得到直线y＝kx+b．①当直线y＝kx+b与线段OC有公共点时，结合图象，直接写出b的取值范围．②当直线y＝kx+b将四边形OABC分成面积相等的两部分时，求k，b．14．已知，y＝ax2+bx﹣3过（2，﹣3），与x轴交于A（﹣1，0），B（x2，0），交y轴于C．（1）求抛物线的解析式；（2）过点C作CD∥x轴，交抛物线于D，是否存在直线y＝kx+1将四边形ACDB分成面积相等的两部分，若存在，请求k的值；若不存在，请说明理由；（3）若直线y＝m（﹣3＜m＜0）与线段AC、BC分别交于D、E两点，则在x轴上是否存在点P，使得△DPE为等腰直角三角形，若存在，请求P点的坐标；若不存在，请说明理由．15．如图，在Rt△ABC中，∠C＝90°，AB＝50，AC＝30，矩形DEFG的顶点G与△ABC 的顶点C重合，边GD、GF分别与AC，BC重合．GD＝12，GF＝16，矩形DEFG沿射线CB的方向以每秒4个单位长的速度匀速运动，点Q从点B出发沿BA方向以每秒5个单位长的速度匀速运动，过点Q作射线QK⊥AB，交折线BC﹣CA于点H，矩形DEFG、点Q同时出发，当点Q到达点A时停止运动，矩形DEFG也随之停止运动．设矩形DEFG、点Q运动的时间是t秒（t＞0）．（1）求线段DF的长；（2）求运动过程中，矩形DEFG与Rt△ABC重叠部分的面积s与t的函数关系式（写出自变量的取值范围）；（3）射线QK能否把矩形DEFG分成面积相等的两部分？若能，求出t值；若不能，说明理由；（4）连接DH，当DH∥AB时，请直接写出t值．16．已知m，n是方程x2﹣6x+5＝0的两个实数根，且m＜n．如图，若抛物线l：y＝﹣x2+bx+c 的图象经过点A（m，0），B（0，n）．（1）求抛物线的解析式；（2）设（1）中的抛物线与x轴的另一个交点为C，抛物线的顶点为D，求C，D的坐标和△BCD的面积；（3）已知P是线段OC上一点，过点P作PH⊥x轴，交抛物线于点H，若直线BC把△PCH分成面积相等的两部分，求P点的坐标．17．【数学经验】三角形的中线能将三角形分成面积相等的两部分．【经验发展】面积比和线段比的联系：如果两个三角形的高相同，则它们的面积比等于对应底边的比．如图1，△ABC的边AB上有一点M，请证明：＝．【结论应用】如图2，△CDE的面积为1，＝，＝，求△ABC的面积．【拓展延伸】如图3，△ABC的边AB上有一点M，D为CM上任意一点，请利用上述结论，证明：＝．【迁移应用】如图4，△ABC中，M是AB的三等分点（AM＝AB），N是BC的中点，若△ABC的面积是1，请直接写出四边形BMDN的面积．18．已知抛物线y＝﹣x2+bx+c的图象经过点A（m，0）、B（0，n），其中m、n是方程x2﹣6x+5＝0的两个实数根，且m＜n．（1）求抛物线的解析式；（2）设（1）中的抛物线与x轴的另一个交点为C，抛物线的顶点为D，求C、D点的坐标和△BCD的面积；（3）P是线段OC上一点，过点P作PH⊥x轴，交抛物线于点H，若直线BC把△PCH 分成面积相等的两部分，求P点的坐标．19．【背景知识】研究平面直角坐标系，我们可以发现一条重要的规律：若平面直角坐标系上有两个不同的点A（x A，y A）、B（x B，y B），则线段AB的中点坐标可以表示为（，）．【简单应用】如图1，直线AB与y轴交于点A（0，3），与x轴交于点B（4，0），过原点O的直线L将△ABO分成面积相等的两部分，请求出直线L的解析式；【探究升级】小明发现“若四边形一条对角线平分四边形的面积，则这条对角线必经过另一条对角线的中点”如图2，在四边形ABCD中，对角线AC、BD相交于点O，S△ABD＝S△BCD．试说明AO ＝CO；【综合运用】如图3，在平面直角坐标系中A（1，4），B（3，﹣2），C（2m，﹣m+5），若OC恰好平分四边形OACB的面积，求点C的坐标．。
因动点产生的面积问题解题策略一.解题策略解读:面积的存在性问题常见的题型和解题策略有两类:图1 图2 图3 计算面积常用到的策略还有:图4 图5 图6例1.已知抛物线y=mx2+(1-2m)x+1-3m与x轴交于不同的两点A、 B.(1) 求m的取值范围;(2) 证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3) 当<m≤8时,由(2)求出的点P和点A、 B构成的△ABP的面积是否有最值,若有,求出最值及相应的m的值;若没有,请说明理由.思路:1. 已知的抛物线的解析式可以因式分解的,抛物线过x轴上的定点(-1, 0).2. 第(2)题分两步,先对m赋予两个不同的值,联立求方程组的解,再验证这个点是确定的.3. 第(3)题中△ABP的高为定值,点A为定点,求△ABP的最大面积,其实就是求点B的横坐标的最大值.例2.问题提出(1) 如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.问题探究(2) 如图2,在矩形ABCD中,AB=4, AD=6, AE=4, AF=2.是否在边BC、CD上分别存在点G、 H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决(3) 如图3,有一块矩形板材ABCD, AB=3米, AD=6米,现想从此板材中截出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,米,∠EHG=45°.经研究,只有当点E、 F、 G分别在边AD、 AB、 BC上时,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能截出符合要求的部件.试问能否截得符合要求的面积尽可能大的四边形EFGH部件?若能,求出截得的四边形EFGH 部件的面积;若不能,请说明理由.图1 图2 图3思路:1. 第(2)题的模型是“打台球”两次碰壁问题,依据光的反射原理.2. 第(3)题需先设AF的长并求解,再验证点H在矩形内部,然后计算面积.例3.如图1,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8, OE=17.抛物线y=x2-3x+m与y轴交于点A,抛物线的对称轴与x轴交于点B,与CD交于点K.(1) 将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①求点F的坐标;②请直接写出抛物线的函数表达式;(2) 将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连结OG,折痕与OG交于点H,点M是线段EH上的一个动点(不与点H重合),连结MG, MO,过点G作GP⊥OM于点P,交EH于点N,连结ON.点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1·S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化的范围;若不变,请直接写出这个值.温馨提示: 考生可以根据题意,在备用图中补充图形,以便作答.图1 备用图思路:1. 第(1)题中点F的位置是由A、 B两点确定的,A、 B两点的坐标都隐含在抛物线的解析式中.2. 第(2)题思路在画示意图过程中,点G是关键点.以E为圆心,EO为半径画弧,交CD于点G.例 4.如图,已知平行四边形ABCD的三个顶点A(n, 0)、 B(m, 0)、 D(0,2n)(m>n>0),作平行四边形ABCD关于直线AD的对称图形AB1C1 D.(1) 若m=3,试求四边形CC1B1B面积S的最大值;(2) 若点B1恰好落在y轴上,试求的值.思路:1. 第(1)题先说理再计算,说理四边形CC1B1B是矩形.2. 第(2)题根据AB1=AB列关于m、 n的方程,整理就可以得到m与n的关系.例5.如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点A(3, 0)和点B(2, 3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=.(1) 求这条抛物线的表达式及对称轴;(2) 连结AB、 BC,求∠ABC的正切值;(3) 若点D在x轴下方抛物线的对称轴上,当S△ABC =S△ADC时,求点D的坐标.解析:1. 直觉告诉我们,△ABC是直角三角形.2. 第(3)题的意思可以表达为: B、 D在直线AC的两侧,到直线AC的距离相等.于是我们容易想到,平行线间的距离处处相等.例6.如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、D分别不与点A、 B重合),点E、 F在AB上,EC⊥CD, FD⊥CD.(1) 求证:EO=FO;(2) 连结OC,如果△ECO中有一个内角等于45°,求线段EF的长;(3) 当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE的面积为S,周长为l,问:S与l是否分别随着x变化而变化?试用所学过的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.思路:1. 用垂径定理和平行线等分线段定理证明点O是EF的中点.2. 第(2)题的△ECO中,∠ECO是定值,45°的角分两种情况.3. 第(3)题用x表示OE的长,在△ECO中,∠ECO是定值.例7.直线y=2x+m与抛物线y=ax2+ax+b都过点M(1, 0),且a<b.(1) 求抛物线顶点Q的坐标(用含a的式子表示);(2) 试说明抛物线与直线有两个交点;(3) 设抛物线与直线的另一个交点为N.①若-1≤a≤-时,求MN的取值范围;②求△QMN的面积最小值.思路:1. 将M(1, 0)分别代入直线和抛物线的解析式,可以确定m的值,用a表示b.2. 联立直线与抛物线的解析式,消去y,得到关于a的一元二次方程,判断Δ>0.3. 第(3)题①,分别求a=-1和a=-时直线与抛物线的交点M、 N的坐标,再求MN的长,两个MN的长,就是MN的取值范围的两端值.例8.已知Rt△EFP和矩形ABCD如图1摆放(点P与点B重合),点F、 B(P)、 C 在同一直线上,AB=EF=6cm, BC=FP=8cm, ∠EFP=90°.如图2, △EFP从图1位置出发,沿BC方向匀速运动,速度为1cm/s, EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连结AF、 PQ.当点Q停止运动时,△EFP也停止运动.设运动时间为t(s)(0<t<6).解答下列问题:(1) 当t为何值时,PQ∥BD?(2) 设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3) 在运动过程中,是否存在某一时刻t,使S五边形AFPQM ∶S矩形ABCD=9∶8?若存在,求出t的值;若不存在,请说明理由;(4) 在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.图1 图2思路:1. 把线段BP、 PC、 CQ、 DQ的长用t表示出来.再把线段BG、 DM的长用t表示出来.2. 用割补法求五边形AFPQM的面积,等于直角梯形减去两个直角三角形的面积.3. 第(3)题用第(2)题的结果,直接解方程就可以了.4. 第(4)题是根据MP2=MG2列方程,需要构造以MP为斜边的直角三角形.例9.如图1,在平面直角坐标系中,过原点O及点A(8, 0)、 C(0, 6)作矩形OABC,连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从点A出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.(1) 如图1,当t=3时,求DF的长;(2) 如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3) 连结AD,当AD将△DEF分成的两部分的面积比为1∶2时,求相应的t的值.图1 图2思路;1. 作DM⊥AB于M, DN⊥OA于N,那么△NDF与△MDE的相似比为3∶4.2. 面积比为1∶2要分两种情况讨论.把面积比转化为两个同高三角形底边的比.3. 过点E作OA的平行线,构造“8字型”相似,这样就把底边的比利用起来了.例10.如图1,二次函数y=x2+bx+c的图象与x轴交于A、 B两点,与y轴交于点C, OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1) 求b、 c的值;(2) 如图1,连结BE,线段OC上点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3) 如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.图1 图2思路：1. 由已知抛物线的解析式可得C(0, c),再用c表示B、 D两点的坐标,然后将B、 D代入抛物线的解析式列关于b、 c的方程组.2. 第(2)题: 通过点C、 F分别与点D、 F'关于直线l对称,得到点F'是BE的中点,从而求得点F的坐标.3. 第(3)题: 设点P的横坐标为m,用m表示点M、 N的坐标,进而用m表示线段PM、 PN、 PA的长,根据两个三角形的面积相等,求出PN边上的高QH.最后讨论NQ与QH的关系.例11.如图,在平面直角坐标系中,直线y=12x+2与x 轴交于点A,与y 轴交于点C.抛物线y=-x 2+bx+c 经过A 、 C 两点,与x 轴的另一个交点为点B.(1) 求抛物线的函数表达式;(2) 点D 为直线AC 上方抛物线上一动点.① 连结BC 、 CD.设直线BD 交线段AC 于点E, △CDE 的面积为S 1, △BCE 的面积为S 2,求 12S S 的最大值; ② 过点D 作DF ⊥AC,垂足为F,连结CD.是否存在点D,使得△CDF 中的某个角恰好等于∠BAC 的2倍?若存在,求出点D 的坐标;若不存在,请说明理由.图1 备用图思路： 1. △CDE 与△BCE 是同高三角形,面积比等于底边的比.构造“8字型”,把底边的比转化为竖直线段的比.2. 第(3)题的第一种情况∠DCF=2∠BAC,过点C 作x 轴的平行线,通过内错角相等,再作轴对称的角,很容易找到点D 的位置.3. 第(3)题的第二种情况∠CDF=2∠BAC,先要探求2∠BAC的大小(正切值),如果这一步探究不出来,基本上进行不下去.例12.已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O 顺时针旋转60°，如题图1，连接BC.（1）填空：∠OBC= ;（2）如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN 的面积为y，求当x为何值时y取得最大值？最大值为多少？思路：（1）由旋转的性质可以证明△OBC是等边三角形，从而可得∠OBC的度数；（2）求出△AOC的面积，利用三角形的面积公式计算即可；（3）分三种情形讨论求解即可解决问题：①当0＜x≤83时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E，利用面积公式表示出△OMN的面积（y值）；②当8 3＜x≤4时，M在BC上运动，N在OB上运动．作MH⊥OB于H，利用∠CBO=60°表示出MH，再利用面积公式表示出△OMN的面积（y值）；③当4＜x≤4.8时，M、N都在BC上运动，作OG⊥BC于G，易求OG，再利用面积公式表示出△OMN的面积（y值），最后分别求出三种情况下面积最大值，从而求出整个运动过程中y的最大值．例13. 在平面直角坐标系中，抛物线2y ax bx c=++交x轴于A、B两点，交y轴于点C（0，43-），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=34.（1）求抛物线的解析式；（2）动点P从点B出发，沿x轴正方向以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P运动到点A时，点Q也停止运动，设运动为t秒.①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由；②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由.思路：本题是代数几何综合题，以平面直角坐标系为背景，考查了求二次函数解析式，二次函数的性质，，方程组的解法，几何图形面积的表示，相似三角形的判定与性质，分类讨论思想，三角形的面积的最值问题，综合性强，难度大，解题的关键是需要学生有良好的运算能力及分析问题和解决问题的能力，还得富有耐心．（1）利用A、B、C三点的坐标确定二次函数的解析式．（2）利用题目的已知条件表示出相关线段的长，①中利用三角函数值探索出∠PAQ=∠ACD，再根据题目中的要求使得△ADC与△PQA相似，进行分类讨论得到对应线段成比例，列出关于t的方程求解即可；②直接利用三角形的面积公式列出△APQ与△CAQ 的面积之和与时间t之间的函数关系式，再将所得的二次函数的解析式配方确定最值即可得到答案.。
所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想 函数思想 方程思想 数形结合思想 转化思想 注重对几何图形运动变化能力的考查从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。
选择基本的几何图形，让学生经历探索的过程，以能力立意，考查学生的自主探究能力，促进培养学生解决问题的能力．图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。
在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展．这些压轴题题型繁多、题意创新，目的是考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等．从数学思想的层面上讲：（1）运动观点；（2）方程思想；（3）数形结合思想；（4）分类思想；（5）转化思想等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热点的形成和命题的动向，它有利于我们教师在教学中研究对策，把握方向．只的这样，才能更好的培养学生解题素养，在素质教育的背景下更明确地体现课程标准的导向．本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点．函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析.一、应用勾股定理建立函数解析式例1(2000年·上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式，并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH中,有长度保持不变的线段，这条线段是GH=32NH=2132⋅OP=2. (2)在Rt △POH 中, 22236x PH OP OH -=-=, ∴N GP B x y2362121xOH MH -==. 在Rt △MPH 中,.∴y =GP=32MP=233631x + (0<x <6). (3)△PGH 是等腰三角形有三种可能情况: ①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意.②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.本专题的主要特征是两个点在运动的过程中，直接或间接地构造了直角三角线，因此可以利用勾股定理去建立函数关系式. 勾股定理是初中数学的重要定理，在运用勾股定理写函数解析式的过程中，主要是找边的等量关系，要善于发现这种内在的关系，用代数式去表示这些边，达到解题的目的. 由于是压轴题，有的先有铺垫，再写解析式；有的写好解析式后，再证明等腰三角形、相似三角形等，还有的再解一些与圆有关的体型. 要认真领会，达到举一反三的目的.1 牢记勾股定理：在直角三角形中，两条直角边的平方和等于斜边的平方.例题，扇形中∠AOB=45°，半径OB=2，矩形PQRS 的顶点P 、S 在半径OA 上，Q 在半径OB 上，R 在弧AB 上，连结OR.（1） 当∠AOR=30°时，求OP 长（2） 设OP=x ，OS=y ，求y 与x 的函数关系式及定义域2 在四边形的翻折与旋转中，往往会应用到勾股定理，由此产生些函数解析式的问题，要熟练掌握.例题：如图，正方形ABCD 中，AB=6，有一块含45°角的三角板，把45°角的顶点放在D 点，将三角板绕着点D 旋转，使这个45°角的两边与线段AB 、BC 分别相交于点E 、F （点2222233621419x x x MH PH MP +=-+=+=E与点A、B不重合）（1）从几个不同的位置，分别测量AE、EF、FC的长，从中你能发现AE、EF、FC的数量之间具有怎样的关系？并证明你所得到的结论（2）设AE=x，CF=y，求y与x之间的函数解析式，并写出函数的定义域（3）试问△BEF的面积能否为8？如果能，请求出EF的长；如果不能，请说明理由.3 在一些特殊的四边形中，如矩形、正方形，它们都是直角，菱形的对角线互相垂直，这些都有可能构造直角三角形，可以考虑用勾股定理写出函数的解析式.例题：如图，在菱形ABCD中，AB=4，∠B=60°，点P是射线BC上的一个动点，∠PAQ=60°，交射线CD于点Q，设点P到点B的距离为x，PQ=y（1）求证：三角形APQ是等边三角形（2）求y关于x的函数解析式，并写出它的定义域（3）如果PD⊥AQ，求BP的值4 作底边上的高，可以构造直角三角形，利用勾股定理写函数的解析式例题：如图，等边△ABC的边长为3，点P、Q分别是AB、BC上的动点（点P、Q与△ABC 的顶点不重合），且AP=BQ，AQ、CP相交于点E.（1）如设线段AP为x，线段CP为y，求y关于x的函数解析式，并写出定义域（2）当△CBP的面积是△CEQ的面积的2倍时，求AP的长（3）点P、Q分别在AB、BC上移动过程中，AQ和CP能否互相垂直？如能，请指出P点的位置，请说明理由.5 在解圆的题目时，首选的辅助线是弦心距，它不仅可以运用垂径定理，而且构造了直角三角形，为用勾股定理写函数解析式创造了条件.例题：如图，⊙A和⊙B是外离的两圆，两圆的连心线分别交⊙A、⊙B于E、F，点P 是线段AB上的一动点（点P不与E、F重合），PC切⊙A于点C，PD切⊙B于点D，已知⊙A 的半径为2，⊙B的半径为1，AB=5.（1）如设线段BP的长为x，线段CP的长为y，求y关于x的函数解析式，并写出函数的定义域（2）如果PC=PD，求PB的长（3）如果PC=2PD，判断此时直线CP与⊙B的位置关系，证明你的结论6 强调圆的首选辅助线是弦心距，它不仅可以平分弦，而且构造了直角三角形，为解题创建新思路.例题：如图，在△ABC中，AB=15,AC=20,cotA=2，P是边AB上的一个动点，⊙P的半径为定长. 当点P与点B重合时，⊙P恰好与边AC相切；当点P与点B不重合，且⊙P与边AC相交于点M和点N时，设AP=x，MN=y.(1)求⊙P的半径(2)求y关于x的函数解析式，并写出它的定义域(3)当AP=65时，试比较∠CPN与∠A的大小，并说明理由阶梯题组训练1 如图，E是正方形ABCD的边AD上的动点，F是边BC延长线上的一点，且BF=EF，AB=12，设AE=x，BF=y.（1）当△BEF是等边三角形时，求BF的长；（2）求y与x之间的函数解析式，并写出它的定义域；（3）把△ABE沿着直线BE翻折，点A落在点A′处，试探索：△A′BF能否为等腰三角形？如果能，请求出AE的长；如果不能，请说明理由.2 如图，在△ABC中，∠ACB=90°，∠A=30°，D是边AC上不与点A、C重合的任意一点，DE⊥AB，垂足为点E，M是BD的中点.（1）求证：CM=EM;（2）如果BC=3设AD=x，CM=y，求y与x的函数解析式，并写出函数的定义域；（3）当点D在线段AC上移动时，∠MCE的大小是否发生变化？如果不变，求出∠MCE的大小；如果发生变化，说明如何变化.3 ABCD中，对角线AC⊥AB，AB=15，AC=20，点P为射线BC上一动点，AP⊥PM(点M与点B分别在直线AP的两侧)，且∠PAM=∠CAD，连结MD.(1)当点M在 ABCD内时，如图，设BP=x，AP=y，求y关于x的函数关系式，并写出函数定义域；(2)请在备用图中画出符合题意的示意图，并探究：图中是否存在与△AMD相似的三角形？若存在，请写出并证明；若不存在，请说明理由；(3)当△为等腰三角形时，求BP的长.4 抛物线经过A（2，0）、B（8，0）、C（0，3316）.（1）求抛物线的解析式；（2）设抛物线的顶点为P，把△APB翻折，使点Pl落在线段AB上（不与A、B重合），记作P′，折痕为EF，设AP′=x，PE=y，求y关于x的函数关系式，并写出定义域；（3）当点P′在线段AB上运动但不与A、B重合时，能否使△EFP′的一边与x轴垂直？若能，请求出此时点P′的坐标；若不能，请你说明理由.5 如图，矩形ABCD中，AD=7，AB=BE=2，点P是EC（包括E、C）上的动点，线段AP的垂直平分线分别交BC、AD于点F、G，设BP=x，AG=y.（1）四边形AFPG是说明图形？请说明理由；（2）求y与x的函数关系式；（3）如果分别以线段GP、DC为直径作圆，且使两圆外切，求x的值.6 在梯形ABCD中，AD//BC，AB⊥AD，AB=4，AD=5，CD=5. E为底边BC上一点，以点E为圆心，BE为半径画⊙E交直线DE于点F.（1）如图，当点F在线段DE上时，设BE=x，DF=y，试建立y关于x的函数关系式，并写出自变量x的取值范围；（2）当以CD为直径的⊙O与⊙E相切时，求x的值；（3）连结AF、BF，当△ABF是以AF为腰的等腰三角形时，求x的值.7 如图，在正方形ABCD中，AB=1，弧AC是以点B为圆心，AB长为半径的圆的一段弧，点E 是边AD上的任意一点（点E与点A、D不重合），过E作弧AC所在圆的切线，交DC于点F，G为切点.（1）当∠DEF=45°时，求证点G为线段EF的中点；（2）设AE=x，FC=y，求y关于x的函数解析式，并写出函数的解析式；（3）将△DEF沿直线EF翻折后得△D1EF，如图2，当EF=65时，讨论△AD1D与△ED1F是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由.（2003年上海第27题）二、应用比例式建立函数解析式例2（2006年·山东）如图2,在△ABC中,AB=AC=1,点D,E在直线BC上运动.设BD=,x CE=y.(1)如果∠BAC=30°,∠DAE=105°,试确定y与x之间的函数解析式；(2)如果∠BAC的度数为α,∠DAE的度数为β,当α,β满足怎样的关系式时,(1)中y与x之间的函数解析式还成立?试说明理由.解:(1)在△ABC中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°.∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°,又∠DAB+∠ADB=∠ABC=75°,∴∠CAE=∠ADB,AEDCB图2∴△ADB ∽△EAC, ∴ACBD CE AB =, ∴11x y =, ∴xy 1=. (2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立, ∴290α-︒=αβ-, 整理得=-2αβ︒90. 当=-2αβ︒90时,函数解析式x y 1=成立. 例3(2005年·上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F. (1)求证: △ADE ∽△AEP. (2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域. (3)当BF=1时,求线段AP 的长. 解:(1)连结OD. 根据题意,得OD ⊥AB,∴∠ODA=90°,∠ODA=∠DEP. 又由OD=OE,得∠ODE=∠OED.∴∠ADE=∠AEP, ∴△ADE ∽△AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠ADO=90°, ∴OD ∥BC, ∴53x OD =,54x AD =, ∴OD=x 53,AD=x 54. ∴AE=x x 53+=x 58. ∵△ADE ∽△AEP, ∴AE AD AP AE =, ∴x x y x 585458=. ∴x y 516= (8250≤<x ). (3)当BF=1时，①若EP 交线段CB 的延长线于点F,如图3(1)，则CF=4.∵∠ADE=∠AEP, ∴∠PDE=∠PEC. ∵∠FBP=∠DEP=90°, ∠FPB=∠DPE,∴∠F=∠PDE, ∴∠F=∠FEC, ∴CF=CE.∴5-x 58=4,得85=x .可求得2=y ,即AP=2. ②若EP 交线段CB 于点F,如图3(2), 则CF=2.类似①,可得CF=CE.∴5-x 58=2,得815=x . 可求得6=y ,即AP=6.A 3(2)3(1)综上所述, 当BF=1时,线段AP 的长为2或6.本专题探究在图形的运动变化过程中，存在平行或相似的三角形，利用比例式来建立函数关系式. 难一些的题目其中的一个变量是比例式，一个变量是线段，也是利用相似或平行来构造比例式，从而写出函数的解析式. 作为最后的一道压轴题，一般情况下写出解析式后还会有一个证等腰或相似或相切的题目，可以二次函数专题中的解题思想进行处理.1 由平行得到比例式，从而建立函数关系式.例题：如图，在△ABC 中，AB=AC=4,BC=21AB ，点P 是边AC 上的一个点，AP=21PD ，∠APD=∠ABC ，连结DC 并延长交边AB 的延长线于点E（1） 求证：AD//BC（2） 设AP=x ，BE=y ，求y 关于x 的函数解析式，并写出它的定义域（3） 连结BP ，当△CDP 与△CBE 相似时，试判断BP 与DE 的位置关系，并说明理由2 由三角形相似得到比例式，建立函数关系式例题：如图，在正方形ABCD 中，AB=2，E 为线段CD 上一点（点E 与点C 、D 不重合），FG 垂直平分AE ，且交AE 于F ，交AB 延长线于G ，交BC 于H.（1） 证明：△ADE ∽△GFA（2） 设DE=x ，BG=y ，求y 关于x 的函数解析式及定义域（3） 当BH=41时，求DE 的长3 在学习利用相似比建立函数的解析式的时候，初中阶段的知识已经学了不少，对最后的压轴题的综合性的要求已经很高了. 一般会在写解析式前有一些证明或计算，写好解析式后再来一个证明等腰三角形或圆的位置关系等. 如果能够把一道复杂的压轴题拆分成几道小的题目，各个击破，难题也就变简单了.例题：如图，在Rt △ABC 中，∠C=90°，sinB=54，AC=4；D 是BC 的延长线上一个动点，∠EDA=∠B ，AE//BC.(1) 找出图中的相似三角形，并加以证明(2) 设CD=x ，AE=y ，求y 关于x 的函数解析式，并写出函数的定义域(3) 当△ADE 为等腰三角形时，求AE 的长4 刚才研究的写函数解析式都是在几何图形中进行的，下面来看在平面直角坐标系中怎样写解析式. 例题：如图，在直角坐标系中的等腰梯形AOCD 中，AD//x 轴，AO=CD=5，OC AD =52，cos ａ=53，P 是线段OC 上的一个动点，∠APQ=∠ａ,PQ 交射线AD 于点Q ，设P 点坐标为（x ，0），点Q 到D 的距离为y（1） 求过A 、O 、C 三点的抛物线解析式（2） 用含x 的代数式表示AP 的长（3） 求y 与x 的函数解析式及定义域（4） △CPQ 与△AOP 能否相似？若能，请求出x 的值，若不能，请说明理由5 当一个变量是比例式，另一个变量是一条线段，怎样来写函数的解析式呢？可以根据题目的要求，由相似三角形面积的比等于相似比的平方，或相似三角形周长的比等于相似比等建立函数解析式.例题：如图，在平面直角坐标系中，点A 的坐标为（1，0），点B 、C 的坐标分别为（-1，0），C （0，b ），且0＜b ＜3，m 是经过点B 、C 的直线，当点C 在线段OC 上移动时，过点A 作AD ⊥m 于点D.(1) 求点D 、O 之间的距离(2) 如果BOCBDA S △△S =ɑ，试求：ɑ与b 的函数关系式及ɑ的取值范围 (3) 当∠ADO 的余切值为2时，求直线m 的解析式(4) 求此时△ABD 与△BOC 重叠部分的面积6 当我们学习到利用相似三角形的相似比来建立函数解析式的时候，初中阶段的知识已经学得差不多了，对于一些貌似很复杂的图形，只要能够分层求解，就能化繁为简.例题：如图，在边长为6的正方形ABCD 的两侧如图作正方形BEFG 、正方形DMNK ，恰好使得N 、A 、F 三点在一直线上，连结MF 交线段AD 于点P ，连结NP ，设正方形BEFG 的边长为x ，正方形DMNK 的边长为y.（1） 求y 关于x 的函数关系式及自变量x 的取值范围（2） 当△NPF 的面积为32时，求x 的值（3） 以P 为圆心，AP 为半径的圆能够与以G 为圆心，GF 为半径的圆相切，若能请求x的值，若不能，请说明理由练习：1. 如图，在三角形中，AB=AC=8，BC=10，点D 、E 分别在BC 、AC 上（点D 不与B 、C 重合），且∠ADE=∠B ，设BD=x ，AE=y.（1） 求y 与x 之间的函数解析式，并写出函数的定义域（2） 点D 在BC 上的运动过程中，△ADE 是否有可能成为一个等腰三角形？如有可能，请求出当△ADE 为等腰三角形时x 的值;如不可能，请说明理由.2. 在△ABC 中，AB=4，AC=5，cosA=53，点D 是边AC 上的点，点E 是边AB 上的点，且满足∠AED=∠A ，DE 的延长线交射线CB 于点F ，设AD=x ，EF=y.（1） 如图1，用含x 的代数式表示线段AE 的长（2） 如图1，求y 关于x 的函数解析式及函数的定义域（3） 连结EC ，如图2，求档x 为何值时，△AEC 与△BEF 相似.3. 如图，在矩形ABCD 中，AB=m （m 是大于0的常数），BC=8，E 为线段BC 上的动点（不与B 、C 重合）.连结DE ，作EF ⊥DE ，EF 与射线BA 交于点F ，设CE=x ，BF=y.(1) 求y 关于x 的函数关系式(2) 若m=8，求x 为何值时，y 的值最大，最大值是多少？(3) 若y=m12，要使△DEF 为等腰三角形，m 的值应为多少？4. 已知在梯形ABCD 中，AD//BA ，AD ＜BC ，且BC=6，AB=DC=4，点E 是AB 的中点.（1） 如图，P 为BC 上的一点，且BP=2. 求证：△BEP ∽△CPD ；（2） 如果点P 在BC 边上移动（点P 与点B 、C 不重合），且满足∠EPF=∠C ，PF 交直线CD与点F ，同时交直线AD 于点M ，那么（3） 当点F 在线段CD 的延长线上时，设BP=x ，DF=y ，求y 关于x 的函数解析式，并写出函数的定义域；（4） 当S △DMF =49S △BEP 时，求BP 的长.5. 如图，在四边形ABCD 中，∠B=90°，AD//BC ，AB=4，BC=12，点E 在边BA 的延长线上，AE=2，点F 在BC 边上，EF 与边AD 相交于点G ，DF ⊥EF ，设AG=x ，DF=y.（1） 求y 关于x 的函数解析式，并写出定义域；（2） 当AD=11时，求AG 的长；（3） 如果半径为EG 的⊙E 与半径为FD 的⊙F 相切，求这两个圆的半径.6. 如图，在半径为5的⊙O 中，点A 、B 在⊙O 上，∠AOB=90°，点C 是弧AB 上的一个动点，AC 与OB 的延长线相交于点D ，设AC=x ，BD=y.(1) 求y 关于x 的函数解析式，并写出它的定义域；(2) 若⊙O 1与⊙O 相交于点A 、C ，且⊙O 1与⊙O 的圆心距为2，当BD=31OB 时，求⊙O 1的半径；(3) 是否存在点C ，使得△DCB ∽△DOC ？如果存在，请证明；如果不存在，请简要说明理由.7. 已知∠ABC=90°，AB=2，BC=3，AD//BC ，P 为线段BD 上的动点，点Q 在射线AB 上，且满足PC PQ =ABAD (如图1所示)（1） 当AD=2，且点Q 与点B 重合时（如图2所示），求线段PC 的长；（2） 在图1中，连结AP. 当AD=23，且点Q 在线段AB上时，设点B 、Q 之间的距离为x ，PBCAPQ S S △△=y ，其中S △APQ 表示△APQ 的面积，S △PBC 表示△PBC 的面积，求y 关于x 的函数解析式，并写出函数定义域；（3） 当AD ＜AB ，且点Q 在线段AB 的延长线上时（如图3所示），求∠QPC 的大小.（2009上海第25题）三、应用求图形面积的方法建立函数关系式例4（2004年·上海）如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时,△AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H. ∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ). (2)①当⊙O 与⊙A 外切时,A B CO 图8 H在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.例2、【09广东】正方形ABCD 边长为4，M 、N 分别是BC 、CD 上的两个动点，当M 点在BC 上运动时，保持AM 和MN 垂直．（1）证明：Rt △ABM ∽Rt △MCN ；（2）设BM =x ，梯形ABCN 的面积为y ，求y 与x 之间的函数关系式；当M 点运动到什么位置时，四边形ABCN 面积最大，并求出最大面积；（3）当M 点运动到什么位置时Rt △ABM ∽Rt △AMN ，求此时x 的值练习1.如图，在△ABC 中，BC=8，CA= ，∠C=60°，EF ∥BC ，点E 、F 、D 分别在AB 、AC 、BC 上（点E 与点A 、B 不重合），连接ED 、DF 。
运动变化中的折叠问题由于动点的运动，导致动直线的位移，使图形在折叠中的重叠部分的面积也发生变化，在这一变化过程中需要对不同情况加以分类讨论。
解决这类折叠中的重叠部分面积问题的试题，关键是找出折痕及全等图形，抓住运动中的不变量，然后利用全等图形和相似图形的性质及相关的知识进行分类求解，问题就会迎刃而解。
下面举例说明如下：一、运动中的折痕与三角形的边平行如果折痕在运动且与三角形一边平行，那么解决这类问题的关键是运用相似三角形的性质，并根据折痕运动，对重叠部分的面积的变化进行分类求解。
例1、（2009恩施市）如图，在中，的面积为25，点为边上的任意一点（不与、重合），过点作，交于点．设，以为折线将翻折（使落在四边形所在的平面内），所得的与梯形重叠部分的面积记为．（1）用表示的面积；（2）求出时与的函数关系式；（3）求出时与的函数关系式；（4）当取何值时，的值最大？最大值是多少？解:(1)∵de∥bc ∴∠ade=∠b,∠aed=∠c∴△ade∽△abc ∴即(2)∵bc=10 ∴bc边所对的三角形的中位线长为5∴当0＜时（3）＜10时，点a’落在三角形的外部,其重叠部分为梯形∵s △a’de=s△ade=∴de边上的高ah=ah’=由已知求得 af=5 ∴a’f=aa’-af=x-5 由△a’mn∽△a’de知∴（4）在函数中∵0＜x≤5 ∴当x=5时y最大为：在函数中当时y最大为：∵＜∴当时，y最大为：二、运动中的折痕与三角形的边垂直如果折痕在运动且与三角形一边垂直，那么解决这类问题的关键是运用直角三角形的性质和锐角三角函数，并根据折痕或图形运动，对重叠部分的面积的变化进行分类求解。
例2、（2008年湖北省荆州市）如图，等腰直角三角形纸片abc 中，ac＝bc＝4，∠acb＝90°，直角边ac在x轴上，b点在第二象限，a（1，0），ab交y轴于e，将纸片过e点折叠使be与ea所在直线重合，得到折痕ef（f在x轴上），再展开还原沿ef剪开得到四边形bcfe，然后把四边形bcfe从e点开始沿射线ea平移，至b 点到达a点停止.设平移时间为t（s），移动速度为每秒1个单位长度，平移中四边形bcfe与△aef重叠的面积为s.（1）求折痕ef的长；（2）是否存在某一时刻t使平移中直角顶点c经过抛物线的顶点？若存在，求出t值；若不存在，请说明理由；（3）直接写出s与t的函数关系式及自变量t的取值范围.解（1）∵折叠后be与ea所在直线重合∴fe⊥ea，rt△abc中，ac=bc，∴∠cab=45°，ef=ea，∠∵，∴oa=oe=1，∴折痕。
重叠面积计算公式在几何学中，重叠面积是指两个或多个形状在空间中重叠部分的面积。
计算重叠面积的公式可以根据具体的形状和情况而有所不同，下面我们将介绍一些常见形状的重叠面积计算公式。
1. 矩形重叠面积计算公式。
当两个矩形重叠时，可以使用以下公式计算它们的重叠面积：重叠面积 = (min(右上角的x坐标) max(左下角的x坐标)) (min(右上角的y坐标) max(左下角的y坐标))。
其中，min和max分别表示取最小值和最大值的函数。
这个公式的原理是通过比较两个矩形的四个边界的位置，找到它们的重叠部分的边界，并计算出重叠面积。
2. 圆形重叠面积计算公式。
当两个圆形重叠时，可以使用以下公式计算它们的重叠面积：重叠面积 = r^2 arccos((d^2 + r^2 R^2) / (2 d r)) + R^2 arccos((d^2 + R^2 r^2) / (2 d R)) 0.5 sqrt((-d + r + R) (d + r R) (d r + R) (d + r + R))。
其中，r和R分别表示两个圆形的半径，d表示两个圆心之间的距离。
这个公式的原理是将重叠部分分成两个扇形和一个三角形，然后分别计算它们的面积并相加。
3. 不规则形状重叠面积计算公式。
对于不规则形状的重叠面积计算，可以使用数值积分或数值逼近的方法来求解。
其中，数值积分是通过将不规则形状分成许多小的子形状，然后对每个子形状的面积进行求和来逼近重叠面积；数值逼近则是通过在不规则形状上放置网格，并计算网格上的点是否在重叠部分内来逼近重叠面积。
以上是一些常见形状的重叠面积计算公式，当然在实际应用中可能还会有其他形状的重叠面积需要计算，这时可以根据具体情况选择合适的方法来求解。
重叠面积的计算在工程、地理信息系统、计算机图形学等领域都有着重要的应用，因此掌握这些计算公式是非常有价值的。
