第三章 正投影与三视图
- 格式:doc
- 大小:893.00 KB
- 文档页数:26


直线的投影[教学目标与要求]一、知识与能力1、掌握直线的投影特性和三面投影;2、掌握各种位置直线的投影特性和求作方法;2、能根据投影正确判断直线段的空间位置。
二、学习方法与素质养成学生自行演示观察,积累感性知识,自觉培养学习能力,学会学习,善于学习,温故知新,举一反三。
[教学重点]直线的三面投影、各种位置直线的投影特性,直线三面投影的求作方法。
[难点分析]直线的命名与空间位置的判别。
[分析学生]1、在学习点的投影的基础上,直线的投影入门不难,难点在于直线的空间位置多样化,初学者对空间直线的各种位置、命名不易把握,容易产生混淆和初记困难。
在教师讲授、演示的基础上,仍需学生通过自己借助于铅笔等直观道具演示观察,来强化感性认识,同时进行反复练习,达到熟练掌握。
[教学设计思路]教学方法:讲练法、演示法、归纳法。
[教学资源]机械制图网络课程,圆规、三角板、教杆等。
[教学安排]2学时(90分钟)。
教学步骤:讲课与演示交叉进行,讲课与练习交叉进行,最后进行归纳。
[教学过程]一、复习回顾(15~10分钟)1、简述点的投影规律,求作点的三面投影的方法,判断重影点的可见性。
2、讲评作业批改情况,纠错。
3、提问教材P.74思考题5、6。
4、预习检测:直线的空间位置有几种?直线段的投影特性是什么?点的投影和直线的投影有什么联系?二、导入新课简述本课主要内容、要点、作用和地位,展示并确认教学目标和要求。
直线的投影是平面投影的基础,也是学习平面立体投影的基础。
三、新课教学(70~80分钟)1、直线的三面投影教师结合教具演示,讲授直线的投影特性和空间位置,在此基础上讲授直线的三面投影,指导学生自己演示、观察直线的三面投影,并讨论归纳其投影特性。
在讲直线的命名时,应引导学生分析直线空间位置及命名的唯一性,增强学生的动手动脑的主动性和探究性学习的兴趣,提高学习成效。
2、直线三面投影的求作教师讲授演示在各种不同条件下,平行线、垂直线、一般位置直线的求作方法,指导学生根据直线的投影特性,利用排除法快速判定其空间位置的技巧。

§3-3点的投影【学习目标】1.识记:点的投影特性点的投影标记2.领会:点的三面投影点的投影规律点的坐标点的投影与坐标两点的相对位置重影点的投影3.应用:点的三面投影点的投影规律点的坐标点的投影与坐标两点的相对位置重影点的投影【重点难点】点的三面投影点的投影规律点的坐标点的投影与坐标两点的相对位置重影点的投影【课前准备】三角尺一付、圆规、HB、B的铅笔两只,两组备一把小刀等作图工具。
【预习导学】1.点的投影特性2.点的投影标记3.点的三面投影4.点的投影规律【学习内容】一、点的投影特性点的投影特性:。
二、点的投影标记空间点用标记,正面投影用标记,侧面投影用标记,水平面投影用标记。
三、点的三面投影从图中可以看出,Aa、A a′、A a″分别为点A到H、V、W面的距离,即:A a = a′a x = a″a y (即a″a YW),反映空间点A到H面的距离;A a′=a a x = a″a z ,反映空间点A到V面的距离;A a″ = a′a z = a a y (即a YH),反映空间点A到W面的距离;上述即是点的投影与点的空间位置的关系,根据这个关系,若已知点的空间位置,就可以画出点的投影。
反之,若已知点的投影,就可以完全确定点在空间的位置。
四、点的投影规律由图中可以看出:a a YH = a′a z 即a′a⊥OXa′a x = a″a YW即a′a″⊥OZa a x = a″a z这说明点的三个投影不是孤立的,而是彼此之间有一定的位置关系。
而且这个关系不因空间点的位置改变而改变,因此可以把它概括为普遍性的投影规律:(1)点的正面投影和水平投影的连线垂直OX轴,即a′a⊥OX;(2)点的正面投影和侧面投影的连线垂直OZ轴,即a′a″⊥OZ;(3)点的水平投影a和到OX轴的距离等于侧面投影a″到OZ轴的距离,即a a x = a″a z 。
(可以用45°辅助线或以原点为圆心作弧线来反映这一投影关系)根据上述投影规律,若已知点的任何两个投影,就可求出它的第三个投影。
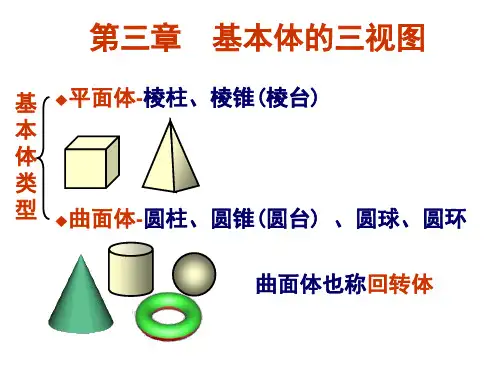





第三章正投影与三视图【知识结构框架】【重点难点提示】l.三视图的形成及投影规律2.点→线→面→基本几何体的技影,空间概念的培养。
【知识要点精讲】一、正投影与三视图:1、投影的概念:灯光或日光照射物体,在墙面或地面上得到影子的现象称为投影。
2、投影法:一组射线通过物体,射向预定平面而得到图形的方法称为投影法。
一组射线——称投影线;其中预定平面——称投影面;得到的图形——称投影。
3、投影法的分类:中心投影法:投影线汇交于一点。
如图3-1。
投影法分两大类正投影:投影钱垂直于投影面。
如图3-2。
平行投影法:投影线相互平行斜投影:投影线倾斜于投影面。
如图3-3。
由于正投影能反映物体的真实形状和尺寸,所以在机械制图中得到广泛应用,绘制机械图样主要采用正投影法。
4、三视图的形成:①设立三投影面体系:如图3-4正投影面V—正立位置;三个相互垂直的投影面水平投影面H—水平位置;侧投影面W—侧立位置。
X轴—H面与V面的交线;三个相互垂直的投影轴 y轴—H面与W面的交线;Z轴—V面与W面的交线。
一个原点O—— X、Y、Z三轴的交点。
②三视图的形成:如图3-5把物体放在三投影面体系中,按正投影的方法分别向三个投影面进行投影,即得到物体的正面投影,水平面技影和侧面投影。
如图3 - 5(a)。
为了方便画图,按GB规定,将三个相互垂直的投影面展开摊平在同一平面上:V面一不动如图3-5(b),即 H面一绕ox轴向下旋转90°W面一绕oz轴向右旋转90°H面上的用"Y H"表示。
注意:展开摊平后,Y轴被分为两部分w面上的用"Yw"表示。
V面上的投影-称主视图展开摊平后: H面上的投影-称俯视图统称三视图。
如图3-5(c)W面上的投影-称左视图去掉投影面范围线(它的大小与视图无关)如图3-5(d),待熟练之后,投影轴也可省略不画。
5、三视图的投影规律:由3-6可见,每个主视图反映物体一个方向的形状,两个方向的尺寸和四个方位。
为方便记①位置关系:【典型图例分析】例一、根据立体图(图3-7)画物体的三视图。
注意:三视图中,不仅整体尺寸符合三等关系,每一局部尺寸也必须符合三等关系。
例二、读懂三视图(图3 -9),想出立体形状,题意分析:本题意图是要求学生运用"三视图的投影规律",分析想象三现图所表达空间物体的结构形状。
读图方法:先整体,后细节,对投影,找关系,联系方位想立体。
读图步骤:①看主、左、俯三个视图,外框均为矩形——空间长方体。
②看主、俯视图—左右分两部分(以虚线为界),右半边长方体无变化。
③看俯、左视图—由前向后分三部分,具体到俯视图可见:是物体的左半边“由前向后分三部分”,且中间部分被切去(对应主视图中的虚线)。
④结合主视图,想清楚前后两部分的形状:前面一块对应主视图中的斜线—空间三角形立板。
后面一块对应主视图的矩形外框—长方体立板(与右半边等高)。
所以综合想象结果如图3 -10。
【同步强化训练】【知识要点精讲】三、点的投影1、点的空间位置:点的空间位置由三个坐标值来确定:A(x,y,z)如图3-11。
表示点A到W面的距离,x越小,离W面越近(越靠右)。
表示点A到V面的距离,Y越小,离V面越近(越靠后)。
表示点A到H面的距离,z越小,离H面越近(越靠下)。
都不为O时,点在空间。
有一个为O时,点在投影面上。
因此,当三个坐标值有两个为O时,点在投影轴上。
都为O时,点在原点上。
2、点的三面投影:①规定:空间点用大写字母表示,如A、B、C、Ⅰ、Ⅱ……V面投影a',b',c',1',2'……投影点用相应的小写字母表示 H面投影a,b,c,1,2……W面投影a",b",c", 1",2"②点的投影特性:点的投影永远是点。
③点的三面投影及技影规律:见图3-12。
为了便于进行投影分析,可按图3-13中的任何一种办法将相邻两投影用细实线连起来。
由图3-13分析可得点的投影规律:a' a⊥OX--A点到W面的距离相等,均为X。
a'a"⊥OZ--A点到H面的距离相等,均为Z。
仍符合"三等"。
aa z= a"a z--A点到V面的距离相等,均为Y。
3、两点的相对位置:①已知坐标值时,由两点的坐标值大小来判断:左右位置由X坐标值来确定,X在者在左,小者在右;前后位置由y坐标值来确定,y大者在前,小者在后;上下位置由z坐标值来确定,z大者在上,小者在下。
②己知投影图时,由投影连线的位置来判断:左右位置由V面和H面投影连线来确定,靠左即左靠右即时右;前后位置由H面和W面投影连线来确定,靠内(距离原点近)即后,靠夕阳距离原点远)即前。
上下位置由V面和W面投影连线来确定,靠上即上,靠下即下。
注意:当两投影点重影时,应将不可见点用括号括起来。
【典型图例分析】例一、己知点A到三个投影面V、H、W的距离分别为15、20、25,试作三面投影图。
题意分析:本题是要求学生掌握点的投影图画法。
作图方法与步骤:1.先画出投影轴,并在ox轴上自原点O向左量取25定出点a z (图3-14a)。
2.过点a z作ox轴的垂线,自a z沿OY H轴方向量取15定出水平投影a;沿OZ轴方向量取20 定出正面投影a',这样就完成了点A的两面投影(图3 - 14h)。
3.若已知一点的两个投影,可根据点的投影规律作出其第三投影,将坐标y=15移到侧面上,就可定出侧面投影a",作法如图3 -14c中箭头所示。
例二、已知A、B、C三点的投影图(图3 - 15),比较其空间位置。
题意分析:本题意图是要求学生掌握两点相对位置的比较方法。
比较方法:据投影图(投影连线)判断。
判断步骤:①以A点为基准,从图中可以看出:b'b连线在a’a边线右边---B点在A点可方;b'b"连线在a'a"连线上边---B点在A点上方:bb"连线比aa"连线距离原点O近---B点在A点后方(近是后面远是前)。
所以,B点在A点的右、上、后方。
②同理可知:C点在B点的正下方,与A点同高(如图3-16)。
【同步强化训练】【知识要点精讲】三、直线段的投影:由初中几何可知:任意两点可以确定一条直线。
因此:直线段的投影是由直线上两点的同名投影(即同一个投影面上的投影)连线来确定的。
如图3-17:1、直线段对一个投影面的技影(单面投影):直线段对-个投影面的相对位置有三种:平行、垂直、倾斜。
不同位置的直线有不同的投影特性,如图3 - 18:①真实性:直线平行技影面,投影实长现C如图3一18(a)。
②收缩性:直线倾斜投影面,投影变短线O如图3 - 18(b)。
③积聚性:直线垂直投影面,投影聚一点。
如图3-18(c)。
2、直线段在三投影面体系中的投影:在三投影面体系中,据直线段相对于三技影面的位置不同可分为三类:水平线投影面平行线正平线侧平线特殊位置直线。
铅垂线投影面垂直线正垂线侧垂线投影面倾斜线----------一般位置直线。
①投影面平行线:平行一个投影面而与另两个投影面倾斜的直线O简记: //一面,∠两面∵在该面:具有真实性,具有收缩性得到:一条实长线,两条变短的直线∴其投影特性为:一条实长线(倾斜于投影轴),两条变短的直线(分别平行于对应的投影,实长在哪个投影面上,就叫哪个技影面的平行线。
如表3 - 10以各投影与投影轴的位置关系而论)②投影面垂直线:垂直一个投影面,必平行于另两个投影面的直线。
简记: ⊥一面,∥两面 ∵ 在该面: 具有积聚性,具有真实性 得到:一个点,两条实长线∴其投影特性为:一个点,两条实长线(分别垂直于对应的投影轴),点在哪个投影面上,就叫哪个投影面的垂直线。
如表3-2。
以各投影与技影轴的位置关系而论)③投影面倾斜线:与三个投影面都倾斜的直线。
简记: ∠三面,∵ 在三个投影面上均具有收缩性, 得到:三条变短的直线。
∴其投影特性为:三条变短的直线(均倾斜于对应的投影轴)。
如图3-17。
以各投影与投影轴的位置关系而论)四、平面形的投影:①不在同一直线上的三点可以确定一个平面。
②一直线和直线外一点可以确定一个平面。
③任意平面形可以确定一个平面。
④平行或相交的两直线也可以确定一个平面。
所以,平面形的投影:就是把平面图形轮廓上的一系列点(多边形各顶点)向投影面投影俨然后按顺序连接即可。
如图3 -19。
实质:仍以点的投影为基础。
1、平面形对一个投影面的投影(单面技影):平面形对一个投影面的相对位置有三种:平行、垂直、倾斜。
不同位置的平面有不同的投影特性:如图3-20。
①真实性:平面平行投影面,投影实形现。
如图3-2O(a)②收缩性:平面倾斜投影面,投影面积变。
如图3-20(b)③积聚性:平面垂直投影面,投影聚成线。
如图3-20(c)2、平面形在三投影面体系中的投影:在三投影面体系中,据平面形相对于三投影面的位置不同可分为三类:水平面投影面平行面- 正平面侧平面特殊位置平面。
铅垂面投影面垂直面- 正垂面侧垂面投影面倾斜面----------一般位置平面。
①投影面平行面:平行一个投影面,必垂直于另两个投影面的平面。
简记:∥一面,⊥两面。
∵在该面:具有真实性,具有积聚性得到:一个实形,两条直线∴其投影特性为:一个实形,两条直线(分别平行于对应的投影轴),实形在哪个投影面中就叫哪个投影面的平行面。
如表3-3:以投影形状而论)②投影面垂直面:垂直一个投影面,而与另两个投影面倾斜的平面。
简记:⊥一面,∠两面∵在该面:具有积聚哇,具有收缩性得到:一条直线,两个类似形∴其投影特性为:一条直线(倾斜于投影轴),两个类似形,直线在哪个投影面上,就叫哪个投影的垂直面。
如表3-4。
以投影形状而论)③投影面倾斜面:与三个投影面都倾斜的平面。
简记:∠三面∵在三个投影面上均具有收缩性得到:三个类似形∴投影面倾斜面的投影特性为:三个类似形。
如图3-19.以投影形状而论)【典型图例分析】例图3 - 21:补画立体的第三投影,并判断直线AB、BD、AD、BG分别是空间何种位置直线。
平面ABD、ABG、BDF分别是空间何种位置平面。
题意分析:此题综合性较强,既要求学生解决“己知点、线、面的两面投影,求第三投影”的问题,又要求学生会分析立体表面及棱线的空间位置,即培养空间概念和综合分析能力。
作图方法:先据点、线、面的投影规律补画立体的第三投影,再按空间直线和平面的投影特性来判断各棱线、表面的空间位置作图步骤:①补画立体的第三技影:如图3-22②分析判断立体表面和棱线的空间位置:(把所分析各棱线、平面的三投影单独画出)【知识要点精讲】五、基本几何体的投影1、常见的基本几何体:如图3-30-----表面均为平面。