7-2平面简谐波的波动方程

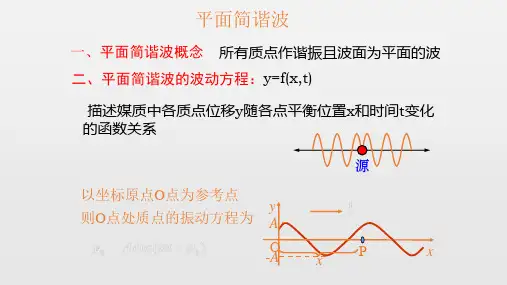
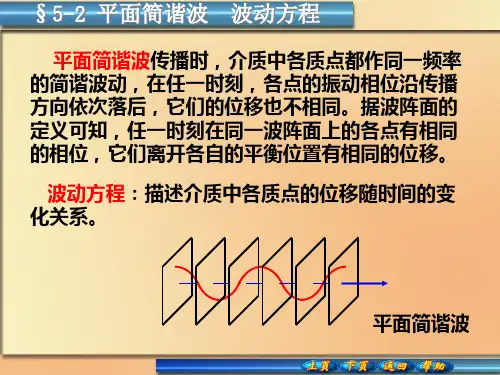
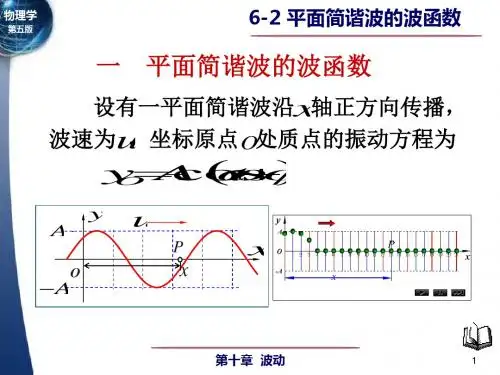
---------------------------------------------------------------最新资料推荐------------------------------------------------------7-2平面简谐波的波动方程§7-2 平面简谐波的表达式___波动的表达式波动方程1/ 28一平面简谐波的波动方程介质中任一质点（同一波线上,坐标为）介质中任一质点（同一波线上坐标为 x）相对其平衡位置的位移（平衡位置的位移（坐标为 y）随时间的变化关系，）随时间的变化关系，称为波动方程. 即 y ( x, t ) 称为波动方程y = y ( x, t )各质点相对平衡位置的位移衡位置的位移波线上各质点平衡位置平衡位置简谐波：在均匀的、无吸收的介质中，简谐波：在均匀的、无吸收的介质中，波源和介质中各质点都作简谐运动时，在介质中所形成的波. 各质点都作简谐运动时，在介质中所形成的波平面简谐波：波面为平面的简谐波平面简谐波：波面为平面的简谐波. 其特点是在均匀的、无吸收的介质中各质点是在均匀的、无吸收的介质中各质点振幅相同均匀的任何复杂的波都可以看成若干个简谐波叠加而成。

任何复杂的波都可以看成若干个简谐波叠加而成。

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 设有一以速度设有一以速度u 沿以速度 x 轴正向传播的平面令原点O 简谐波 . 令原点的初相为零，的初相为零，其振动方程波动方程的推导设x = 0,0 = 0时间推迟方法yO = AcosωtyO = Acosωt点O 的振动状态t-x/u时刻点的运动状态时刻点O 时刻点点P 振动方程x yP = Acosω(t ) u=x t = u点Pt 时刻点 P 的运动状态3/ 28波动方程y AOx y = A cos ω ( t ) u相位落后法uPAx*λx点 P 比点 O 落后的相位y o = A cos ω t x = p O = 2πy p = A cos(ωt + p )点 O 振动方程设 x = 0 ,0= 0x x p = 2π = 2π = ω λ Tu u点 P 振动方程xλx yp = Acosω(t ) u---------------------------------------------------------------最新资料推荐------------------------------------------------------ 如果原点的初相位不为零yAuλx = 0 , ≠ 0点 O 振动方程xAOyO = A cos(ωt + )波动方程x y = A cos[ω (t ) + ] u 沿 x 轴正向u x y = A cos[ω (t + ) + ] u 沿 x 轴负向 u5/ 28波动方程的其它形式y(x, t) = Acosω[(t x) +] u2π ω= Tω2π 2π = = u Tuλt x y(x,t) = Acos[2 π( ) +] T λ π 1 2 v= =2 v πT T---------------------------------------------------------------最新资料推荐------------------------------------------------------ 质点的振动速度，质点的振动速度，加速度y x v = = ωAsin[ω(t ) +] t u2 y x 2 a = 2 = ω Acos[ω(t ) +] t u严格区分两种速度(波速和严格区分两种速度(波速和振动速度)波速(相速波速相速) 相速u=λT=ν λy x v = = ωAsin[ω(t ) +] t u7/ 28二波动方程的物理意义x t x y = A cos[ω (t ) + ] = A cos[2 π( ) + ] u T λ1 当 x 一定时，波动方程表示该点质点的简谐一定时，振动方程，振动的相位差. 振动方程，并给出该点与点 O 振动的相位差x x 0 x = [ω (t ) + ] [ω (t ) + ] = ω = 2π u u u λx x = ω = 2 π u λω=2π u波具有时间的周期性-y ( x , t ) = y ( x , t + T ) （波具有时间的周期性振动周期性）λ---------------------------------------------------------------最新资料推荐------------------------------------------------------ 波线上各点的简谐运动图波具有时间的周期性-（波具有时间的周期性振动周期性）9/ 28x t x y = A cos[ω (t ) + ] = A cos[2 π( ) + ] u T λ2 当一定时，波动方程表示该时刻波线上各点相对一定时，其平衡位置的位移，其平衡位置的位移，即此刻的波形（广角镜头拍照片—定格）t波具有空间的周期性）y ( x, t ) = y ( x + λ , t ) （波具有空间的周期性）波程差 x21 = x2 x1波线上点x1与点的位相差波线上点与点x2的位相差与点波程差与位相差---------------------------------------------------------------最新资料推荐------------------------------------------------------ 3 若 x, t 均变化，波动方程表示波形沿传播均变化，方向的运动情况. 方向的运动情况yOut时刻t + t 时刻x时到t+x时 : 从t 时到时到时波线上各质点的相位均向前传播 x 即:x x = u x t （行波）行波）11/ 28已知波动方程如下，求波长、周期和波速. 例1 已知波动方程如下，求波长、周期和波速y = (5cm) cosπ [(2.50s -1 )t (0.01cm -1 ) x].解：（比较系数法）设波动方程为: 比较系数法）设波动方程为t x y = A cos 2π ( ) T λ把题中波动方程改写成比较得2.50 -1 0.01 -1 y = (5cm ) cos 2π [( s )t ( cm ) x ] 2 2λ 2cm 2 1 = 200 cm u = = 250cm s T = s = 0.8 s λ = T 0.01 2.5---------------------------------------------------------------最新资料推荐------------------------------------------------------ 例2平面简谐波y = 0.02 cos π (5 x 200t )式中 x，y 以（m）计，t 以（s）计。

，））（1）求振幅、波长、频率、周期和波速。

）求振幅、波长、频率、周期和波速波形图。

（2）画 t = 0.0025 s 波形图。

）13/ 28设波动方程为: 解：(1)设波动方程为设波动方程为 t x y = A cos 2π T λ 此波可变为y = 0.02 cosπ (5x 200t )x t = 0.02 cos 2π 0.01 0.4 比较有A = 0.02(m ) T = 0.01(s ), λ = 0.4(m ) ，1 ν = = 100 T(Hz ) ，u = λ ν = 40(m s1)---------------------------------------------------------------最新资料推荐------------------------------------------------------ （2）先求 t = 0 时波形方程并画波形图：x t y = 0 . 02 cos 2 π 0 .4 0 . 01= 0.02cos5πx(m) (周期= 波长λ = 0.4m) :t = 0→0.0025(s)，波向 x 轴正向前进距离，y (m ) x = u t = 40 × 0.0025 = 0.1m = 1 λ0.024O 0.1 0.2 0.3 0.4x(m )方法二:也可将代入波动方程，方法二也可将 t = 0.0025(s)代入波动方程，求得波形方程代入波动方程y=0.02cos(5πx-π/2), 然后画出波形图然后画出波形图15/ 28轴正方向传播，例3 一平面简谐波沿 O x 轴正方向传播，已知振幅 A = 1.0m ， = 2 . 0 s ， = 2.0m . 在 t = 0 时坐标T λ 原点处的质点位于平衡位置沿 O y 轴正方向运动 . 求解设原点处振动方程为 1）波动方程）y = A cos( ω t + )Ot = 0Ay ωy = 0, v > 0y = cos( ω t ππ =2x π t x π y = cos[ω(t ) ] = cos[2π ( ) ] u 2 2 2 22 所以波动方程为x t x y = A cos[ ω ( t ) + ] = A cos[ 2π ( ) + ] u T λ)m---------------------------------------------------------------最新资料推荐------------------------------------------------------ 2）求 t = 1 . 0 s 波形图）波形图.波形方程波形图为t x π y = 1.0 cos[ π( ) ] m 2 2.0 2.0 2 π y =1.0cos( π x) m t = 1 .0 s 2= 1.0 sin(π x)my/m1.0o-1.02.0x/mt = 1 . 0 s 时刻波形图17/ 283） x = 0 .5 m 处质点的振动规律并做图 . ）x = 0.5m 处质点的振动方程t x π y =1.0cos[ π( ) ] 2 2.0 2.0 2m注意:旋转矢量转了注意旋转矢量转了π/2 旋转矢量转了y = cos( π t π )y3 4Om3 *y/m1.0 2 0 -1.0*1 2 * 4 *1ω1.02.0**t /sx = 0.5 m 处质点的振动曲线---------------------------------------------------------------最新资料推荐------------------------------------------------------ 沿直线传播,波例4 一平面简谐波以速度u = 20m / s 沿直线传播波线上点 A 的简谐振动方程yA = 3×102 cos4 πt mu8m C B 5m 9m DoA =0x1）以 A 为坐标原点，写出波动方程）为坐标原点，A = 3×10 m设波动方程为: 设波动方程为2T=2πω= 0.5sλ = uT = 10 mt x y = A cos[ 2π ( ) + ] T λ19/ 282）以 B 为坐标原点，写出波动方程）为坐标原点，y A = 3×10 cos 4 π t2mu8m C 5m 9m A DoBBAx=π B A = 2πB =πλ5 = 2π 102A = 0my B = 3 × 10 cos(4 π t + π )---------------------------------------------------------------最新资料推荐------------------------------------------------------ 3）写出传播方向上点C、点D 的简谐振动方程）写出传播方向上点t x 2 以为坐标原点) y = 3×10 cos 2 π( ) m (以A为坐标原点 0.5 10 u8m 5m 9m C B o A D 将点 C 坐标:x=-13m代入波动方程坐标x坐标:x=9m代入波动方程将点 D 坐标21/ 284）分别求出 BC ，CD 两点间的相位差）(以A为坐标原点以为坐标原点)u8m C B 5m 9m Dλ = 10moAx---------------------------------------------------------------最新资料推荐------------------------------------------------------ 总结:求解波动方程方法总结求解波动方程方法1、求出坐标原点 O 振动方程、2、得出波动方程、yO = A cos(ωt + )3、波动方程其它形式、波动方程其它形式x y = A cos[ ω ( t ) + ] 沿 ox 正向传播u x y = A cos[ ω ( t + ) + ] 沿 ox 负向传播 ut x y = Acos[2 π( ) +] T λ23/ 28讨论y1）给出下列波动方程所表示的波的传播方）给出下列波动方程所表示的波的传播方点的初相位. 向和 x = 0 点的初相位变成波动方程的标准形式x t x y = A cos ω ( t ) = A cos 2 π ( )Tt x = Acos[2 π( ) +π ] T λ 向 x 轴正方向传播= πλ2）平面简谐波的波动方程为 y = A cos( Bt Cx ) ）为正常数，求波长、波速、式中 A , B , C 为正常数，求波长、波速、波传播方的两点间的相位差. 向上相距为 d 的两点间的相位差x u = Acosω[(t + ) +π ) u 向x 轴负方向传播= π2π B= T 2π T= By = A cos( Bt Cx )C= 2π对比λt x y = A cos 2 π ( ) T λ 2 πλ= C2π λ= CB d = 2 π = dC u= = λ T Cλ---------------------------------------------------------------最新资料推荐------------------------------------------------------ 思考: 思考:t=T/4时, a,b,c各质点运动方向如何?3 ）如图简谐波以余弦函数表示，以余弦函数表示，求 O、a、b、c 各点振动初相位初相位(t=0). 点振动初相位t =0At =T/4 +tyaub ct=T/4O ( π ~ π )AλxωOAωωOyo = ππ a = 2A b = 0yAOyOAωyπ c = 225/ 28课堂练习: 课堂练习7-1-6, 7-2-3,7-3-2---------------------------------------------------------------最新资料推荐------------------------------------------------------ 作业: 作业: 7-1-5, 7-1-10, 7-3-1 77-27/ 28二、横波和纵波 (波的两种基本类型)横波：质点振动方向与波的传播方向相垂直的波横波：质点振动方向与波的传播方向相垂直的波. 垂直的波（仅在固体中传播）特征：具有交替出现的波峰和波谷特征：具有交替出现的波峰和波谷.。