当前位置：文档之家 › 平面波的波动方程

平面波的波动方程

  • 格式：ppt
  • 大小：216.00 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

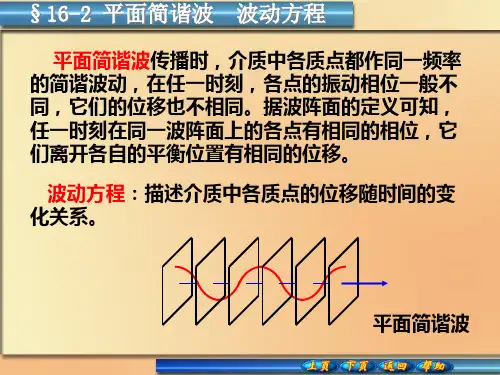
平面简谐波__波动方程

平面简谐波__波动方程
若振动从O 传到P所需的时间为t，在时刻t，P点处质点
的位移就是O 点处质点在t – t 时刻的位移，从相位来说，
P 点将落后于O点，其相位差为 t。
P点处质点在时刻t 的位移为：
yP (t) Acos t t' 0
平面简谐波的波动表式
因 t' x u
yP (t)
A cos
t
x u
的相位落后 。
(7)3T/4时的波形如下图中实线所示，波峰M1和M2已
分别右移3 而4 到达
y /cm
和M1' 处M。2 '
0.5 M1
M1' M2
M2'
0.4
0.2
a
0
b
0.2 10 20 30 40 50 60 70 x /cm
0.4
0.5
t=3T/4
波动方程的推导
(5)质点的最大速率
vm
波动表式的意义：
x 一定。令x=x1，则质点位移y 仅是时间t 的函数。
即
y
A cos
t
2
x1
0
上式代表x1 处质点在其平衡位置附近以角频率
作简谐运动。
y
A
O
t
t 一定。令t=t1，则质点位移y 仅是x 的函数。
平面简谐波的波动表式
即
y
A cos
t1
2
x
0
以y为纵坐标、x 为横坐标，得到一条余弦曲线，
t 2
)
球面波的余弦表式如下：
a r
cos
t
r u
0
a —r —振幅
3. 波动方程的推导
设固体细长棒的截面为S、密度为

波函数的几种不同的形式

波函数的几种不同的形式

r1 ) 2n
n 0,1,2,3,.....
A Amax A1 A2
干涉减弱 的条件：
( 20
10
)
2
(r2 r1 ) (2n 1)
n 0,1,2,3,.....
A Amin | A1 A2 |
当两波源的初相位相同时，相干条件可写为：为波程差
干涉加强 r2 r1 n n 0,1,2,3,...
t
u
显然能流是随时间周期性变化的。但它总为正值。
2)平均能流:在一个周期内能流的平均值称为平均能流。
P u S
3)能流密度:通过垂直于波动传播方向的单位面积的平均能流 称为能流密度或波的强度。
I P u 1 A2 2u
S
2
能流密度是单位时间内通过垂直于波速方向的单位截面的
平均能量。
I
1
A2
注意： 波的叠加原理仅限于线性波动现象， 例如对强冲击波则不成立。
三、弦上横波的反射与透射
定义媒质特征阻抗: Z u 媒质密度，u 波速
1、振幅
振幅反射系数
B Z1 Z2 A Z1 Z2
A 入射波振幅
振幅透射系数
C 2Z1 A Z1 Z2
B 反射波振幅 C 透射波振幅
2、能量＝1 2 A2 , I 1 2 A2u 1 2 A2 Z
3、驻波的特征： y y1 y2 2 Acos kx cost
①波节和波腹： 有些点不动(波节),有些点振动最强(波腹)
波节：振幅为零的点称为波节。
| 2 Acos 2 x | 0 即: 2 x (2n 1) 的各点。
2
波节的位置为： x (2n 1)
4
n 0, 1, 2y...

11-3 波动方程 波速

11-3 波动方程 波速

E 杨氏模量
上页 下页 返回 退出
2.体变
F
V V
压强增量与体积增量成正比
p k V V
k 体积模量
上页 下页 返回 退出
3.切变
F
S
切应力 F S
S
切应变
F G
S
G 切变模量
F
它们成正比：
上页 下页 返回 退出
x2 F t2
波速 u F
l
上页 下页 返回 退出
三、波速
柔软细绳和弦中横波 固体内纵波
u F
l
u E
固体内横波
u G
E固体杨氏模量，G剪切模量， 密度
上页 下页 返回 退出
*四、介质的形变及其模量
1.线变
F
l
F
l l
截面积S 正应力 F 线应变 l
S
l
实验表明，在弹性范围内
F E l Sl
o Fa
x
合力
Fy Fb sinb Fa sina F(sinb sin a )
上页 下页 返回 退出
对于微小扰动 sina tana ，sinb tanb
而且 tan y 可得：
x
Fy
F
y x
b
y x
a
F
2 y x2
x
由牛顿定律，可得
Fy
may
l x
2 y x2
2 y l 2 y
在三维空间中的一切波动过程，只要介质无吸收 且各向同性，都适合下式：
2
x2Biblioteka 2y 22
z 2
1 u2
2
t 2
代表振动位移。
球面波的波动方程：2 (r

平面简谐波概念

平面简谐波概念

解：
•
（1）T 2， 40，u 2０，A 10， 2
T
T
且t 0时：yo 5，vo 0
O

2 3

(2) OB长度
Y(cm)
10 •
u
-5 •
解：O B （O B）2
oB
C
20
-5
x(cm)
•
t 0时：yB 0，vB 0
O
-A
x
P
x
P点比O点超前时间 反向波波函数
y
O
P
x
x
以波线上x0处点为参考点
y
则Q点处质点的振动方程为 A x0 Q
O -A
x
P
x
Q点的任一振动状态传到P点，需要时间
则波动方程：
其中：x xo u
— 表示x处质元的振动落后(或超前）xo处质元
振动的时间
(
x u
xo
)
—
表示x处质元的振动落后(或超前）于xo处质元
(2)同一时刻,沿波线各质元振动状态不同,各质元相位 依次落后
*u
=

T
=
u由介质的性质决定
T T振
振 由振源决定.
得波动方程:
当x确定: y(t)——x处质元的振动方程 当t确定： y(x)——t时刻的波形
二、波的强度
1、能流P : 单位时间通过某一面积的波能 P su
—单位:焦耳/秒米2
波动在无吸收的、均匀无限大介质中传播，
1、平面波：A保持不变。
1
2
2、球面波：A与r成反比。 证明：1、 无吸收， P1 P2

波动光学公式复习

波动光学公式复习

波动光学公式复习波动光学是物理学的一个分支，研究光的传播和相互作用的波动性质。

波动光学的基础是波动理论，利用波动方程和边界条件，可以推导出一系列关于光波的性质，并且与实验结果相符。

在本篇复习中，我将回顾波动光学的一些重要公式。

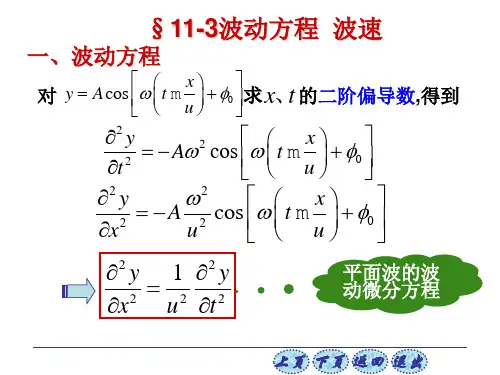
1.波动方程波动方程是描述波的传播的微分方程。

对于光波，我们可以采用波动方程来描述光的传播行为。

波动方程如下：∇^2ψ-1/c^2∂^2ψ/∂t^2=0其中，∇^2是拉普拉斯算子，ψ是波函数，c是光速。

2.平面波的描述平面波是具有相同频率和波矢的波，具有以下形式的解析表达式：ψ(x,t) = A * e^(i(kx - ωt))其中，A是振幅，k是波矢，x是位置，ω是角频率，t是时间。

平面波描述了波的传播过程，并且可以通过叠加多个平面波得到复杂的波形。

3.折射定律折射定律描述了光线从一个介质射入另一个介质时的偏折现象。

根据斯涅耳定律，入射角i和折射角r满足以下关系：n1 * sin(i) = n2 * sin(r)其中，n1和n2分别是两个介质的折射率。

折射定律告诉我们光线由一种介质传输到另一种介质时的偏折角度，进而影响到光的传播方向。

4.衍射公式衍射是光线通过一个较小孔径或障碍物后产生的弯曲现象。

根据菲涅尔衍射公式，衍射极大值的位置可以由以下方程给出：sin(θ) = nλ/a其中，θ是衍射角，λ是光的波长，a是孔径或障碍物的大小。

衍射公式告诉我们衍射现象的出现与波长、孔径或障碍物的大小有关。

5.直线偏振光直线偏振光是在一个平面上振动的光波，具有以下表达式：ψ(x,t) = A * cos(kx - ωt + φ)其中，A是振幅，k是波矢，x是位置，ω是角频率，t是时间，φ是相位差。

直线偏振光是光学中常见的一种偏振光，其振动方向是固定的。

6.光的干涉干涉是当两束或多束光波相遇时，它们会叠加产生明暗相间的条纹。

根据叠加原理，两束光波的干涉可以通过相干光的波函数叠加得出：ψ(x,t)=ψ1(x,t)+ψ2(x,t)其中，ψ1和ψ2是两束光波的波函数。

平面波的波动方程

平面波的波动方程

探究平面波的波动方程
平面波是物理学中一种基本的波动形式，它在自然界中有着广泛的应用。

其中平面波的波动方程是研究平面波特性的重要基础。

本文将详细讲解平面波的波动方程，并深入探讨其物理意义。

平面波是指波的振动方向垂直于波传播方向的波动形式。

在数学上，平面波可以用以下公式表示：
A = A0sin(kx - ωt + φ)
其中A是波的振幅，k是波数，x是波的传播方向，t是时间，ω是角频率，φ是初相位。

根据波的定义，平面波的波动方程可以表示为：
∂2A/∂x2 = (1/v2)∂2A/∂t2
其中v是波的速度。

将平面波的表达式代入波动方程中，可得：
-k2A0sin(kx - ωt + φ) = (1/v2)(ω2A0sin(kx - ωt + φ)/∂t2)
整理后可得到平面波的波动方程：
∂2A/∂x2 + k2A = (ω2/v2)A
通过对波动方程的分析，我们可以得到以下结论：
1. 平面波的波动方程是二阶偏微分方程。

2. 平面波的波数k与角频率ω满足波速公式v = ω/k。

3. 平面波的波动方程可以描述出平面波的传播和振动状态。

通过以上的分析，我们可以进一步探讨平面波的物理意义。

首先，平面波的波动方程告诉我们，平面波的传播速度与波长和频率有关。

其次，平面波的波动方程将平面波的传播和振动状态联系在了一起，
揭示了平面波的本质特性。

总之，平面波的波动方程是研究平面波特性的重要基础。

通过对
波动方程的分析，我们可以深入探讨平面波的物理意义，并为平面波
的应用提供理论基础。

4_2_2波动方程、波的能量、声波

4_2_2波动方程、波的能量、声波
引子： 引子：悬浮的小动物 究竟是什么力量使小 动物悬浮在空中的？ 动物悬浮在空中的？ 答案在本次讲课中。 答案在本次讲课中。
§2.4 波动方程与波速
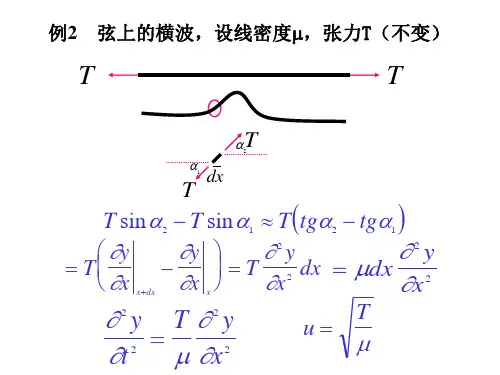
一、波动方程 简谐波的波函数为： 简谐波的波函数为： y(x,t)=Acosk(ut-x) 2 y y = k 2u2 A sin k(ut x) = kuAsin k(ut x) 2 t t y 2 y = kAsin k(ut x) = k 2 A sin k(ut x) x x 2 2 2 y 2 y =u --- 平面波的波动方程 平面波的波动方程 2 2 t x 其通解为 y = f1 ( x + ut ) + f 2 ( x ut ) --- 平面波函数 平面波函数 u 为波速
w = w
k
W V
p
1 y = E 2 x
2
2
+ w
p
1 y 1 y = ρ + E t x 2 2
2
3.能量密度 能量密度 w = w
k
+ w
p
1 y 1 y = ρ + E t 2 2 x
E ρ
2
2
棒中纵波速度 u =
E = ρu 2
1 2 y w p = ρu 2 x
1 y = ρ t 2
2
2.势能密度 势能密度
--- 与弹性（形变）有关 与弹性（形变）
考虑一棒的线变， 考虑一棒的线变， 棒长： 截面： 棒长：l ，截面：S 两端拉力： 两端拉力：由0 → F 相应形变：增至 ， 应变。 相应形变：增至l，应力 ∝ 应变。
F ES l =E F= l = kl S l l 1 2 k (l ) 势能： W p = 势能： 2

物理学14-平面简谐波的波函数与波动方程

物理学14-平面简谐波的波函数与波动方程

若波源（原点）振动初位相不为零 y0 A cos( t 0 )
x y A cos[ (t ) 0 ] u
或
t x y A cos[ 2 ( ) 0 ] T 2x y A cos[ 2t ) 0 ] 2 y A cos[ (ut x) 0 ] A cos[ k (ut x) 0 ]
y
O
u
x
x
p
x O点振动状态传到p点需用 t u t 时刻p处质点的振动状态重复
y
O
u
x
x
p
x t 时刻O处质点的振动状态 u
x p点的振动方程： y A cos ( t ) u 沿x轴正向传播的平面简谐波的波动方程
沿着波传播方向，各质点的振动依次落后于波源振动 x 为p点的振动落后与原点振动的时间 u x 沿x轴负向传播的 y A cos ( t ) 平面简谐波的波动方程 u
在时间t内整个波形沿波的 传播方向平移了一段距离x
y
O
u
t
t t
x x
x
可见，波函数y(x,t)反映了波形的传播。 它描述的是在跑动的波，这种波被称为 行波（travelling wave）
三、平面波的波动微分方程
x y A cos[ ( t ) 0 ] u
求t 的二阶导数
2x0

若x0= 则 x0处质点落后于原点的位相为2
为x0处质点落后于原点的位相
是波在空间上的周期性的标志
同一波线上任意两点的振动位相差 x2 x1 x 2 1 2 2


பைடு நூலகம்
2、如果给定t，即t=t0 则y=y(x) Y x y A cos[ ( t 0 ) 0 ] u 表示给定时刻波线上各质 O 点在同一时刻的位移分布 ，即给定了t0 时刻的波形

波函数几种不同形式

波函数几种不同形式
2、产生干涉的条件：
两波源具有相同的频率。
两波源具有恒定的相位差。 满足上述条件的称为相干波。 两波源的振动方向相同
两波源的波振幅相近或相等时干涉现象明显。
3、干涉加强、减弱条件：
s1
r1
p
设有两个频率相同的波源 S1S2 的振动表达式为：
y10 (s1 , t ) A10 cos(t 10 )
的变化和动能的变化“步调一致”。
3)总机械能:
E
Ek
E p
VA2 2
s in2 [ ( t
x u
)
0
]
4)能量密度:( 单位体积中的能量 )
E
V
A2
2
s in2 [ ( t
x u
)
0
]
5)平均能量密度( 在一个周期内的能量密度的平均值)
1
T
T
dt
0
1 T
T 0
A2
2
s in2 [ ( t
2 y t 2
即y1、y2 分别是它的解，则它们的任一线性组合y=C1 y1+C2 y2
也是方程的解,即上述波动方程遵从叠加原理。
实际表现：
❖ 无论是否相遇, 各列波将保持原有的特性( 频率, 波长和
振动方向等)不变, 按照原来的方向继续前进, 就象没有
遇到其他的波一样。
❖ 在其相遇区域内, 任一点处质点的的振动为各个波单独 存在时所引起的振动的矢量和。
波函数的几种不同的形式：
y( x, t )
A cos[ (t
x u
)
0
]
1 , 2
T
u
T
y( x, t )
Acos[2 ( t

波函数的几种不同的形式

波函数的几种不同的形式

1 2
u 2 A12 S1T
1 2
u 2 A22 S2T
S1 4r12 ; S2 4r22
r2
r1
A1r1 A2r2
所以球面波的振幅与离波源的距离成反比。
如果距波源单位距离的振幅为A则距波源r处的振幅为 A r
由于振动的相位沿波速方向随距离的增加而落后的关系， 与平面波类似，球面简谐波的波函数：
x) u
0
]d t
1 A22
2
A2,2
特点:
A2 2
s in2 [ ( t
x u
)
0
]
x, t
A、Ek Ep 相位,大小均相同；机械能不守恒。
( 注意与振动能量相区别 )
y
•c
y
•c
O
•B
x
• A 波形图
O•
•B
t
• A 振动图形
平衡位置（y = 0） E k 、 E p 最大。 振幅处（y = A） E k 、 E p 为 0。 B、若x 一定, E k 、 E p、E 均随 t 周期性变化。
t
u
显然能流是随时间周期性变化的。但它总为正值。
2)平均能流:在一个周期内能流的平均值称为平均能流。
P u S
3)能流密度:通过垂直于波动传播方向的单位面积的平均能流 称为能流密度或波的强度。
I P u 1 A2 2u
S
2
能流密度是单位时间内通过垂直于波速方向的单位截面的
平均能量。
I
1
A2 2u
1、平面波 在均匀不吸收能量的媒质中传播的平面波 在传播方向上振幅不变。
证明：因为
在一个周期
T内通过
S1和

平面波的波动方程

平面波的波动方程

1
2
2
2k
1
2
n
2k
1
2n，PQ
3 2
R为PQ连线上任一点，求R点振动的振幅
3
2
P
QR
解: kr r
1
2
1
2
3
k 3 减弱
2
A0
三、驻波
当两列振幅相同，频率相同，振动方向相同的 波以相反方向传波时，叠加形成驻波。
1. 演示： Zlcai
频率范围 20 20000Hz
声强级
I L log
I 0
单位：贝尔（bel）
分贝(dB）
I 1012W / m2 0 1
1dB bel 10
声波, 超声波，次声波
§17－8 波的叠加 波的干涉
一、波的叠加原理 １.波的独立性原理 几个波源产生的波，在传播过程相遇时,每个波的 波长，频率，振动方向，传播方向都不因其它波 的存在而改变。即各个波相互间没影响，每个波 的传播就象其单独存在时一样。
n L n 1,2,3 2
u nu
2L
n = 1,2,3 简正频率
对应的驻波称为弦的简正模或固有振动
n1
n2
例、如图所示，在一根线密度μ=10－3kg/m和张力
F=10N的弦线上,沿x轴正方向传播简谐横波,其频率
ν=50Hz,振幅A=0.04m。巳知弦线上离坐标原点 X负1向=0运.5m动处,当的波质传点播在到t=x02=时1刻0m的处位固移定为端+时A2 ,,被且全沿部y轴反 射。试写出:
解满足叠加原理。 •光波在媒质中传播时 弱光 媒质可看作线性媒质 强光 媒质非线性,波的叠加原理不成立
二、波的干涉
１.相干条件 频率相同，振动方向相同，相位差恒定

波传播所满足的波动方程

波传播所满足的波动方程

波传播所满足的波动方程
波传播所满足的波动方程可以根据具体情况而定。

以下是几个常见的波动方程：
1. 一维波动方程：
∂²u/∂t² = c² ∂²u/∂x²
其中，u(x,t)代表波的位移，c为波速，x为空间坐标，t为时间。

2. 二维波动方程（横波）：
∂²u/∂t² = c² (∂²u/∂x² + ∂²u/∂y²)
其中，u(x,y,t)代表波的位移，c为波速，x和y为平面上的空间坐标，t为时间。

3. 三维波动方程（横波）：
∂²u/∂t² = c² (∂²u/∂x² + ∂²u/∂y² + ∂²u/∂z²)
其中，u(x,y,z,t)代表波的位移，c为波速，x、y和z为空间坐标，t为时间。

需要注意的是，不同类型的波（例如横波或纵波）以及不同的介质（例如固体、液体或气体）可能有不同的波动方程。

此外，上述方程还是基于经典的波动理论，实际情况可能需要考虑更复杂的因素。

平面简谐波的波动方程三种形式

平面简谐波的波动方程三种形式

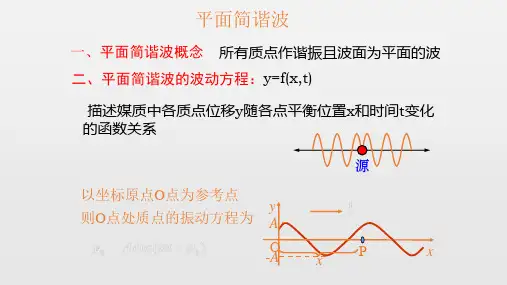
一、平面简谐波的概念平面简谐波是一种特殊的波动现象，它具有特定的波动方程和波动特性。

简谐波的振幅随时间以正弦或余弦函数变化，具有周期性和频率性，是物理学中常见的一种波动形式。

二、平面简谐波的波动方程1. 时间域的波动方程在时间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

2. 空间域的波动方程在空间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

3. 复数形式的波动方程在复数形式下，平面简谐波的波动方程可以表示为：\[y(x,t) = A\cos(kx - \omega t + \phi) = \Re(Ae^{i(kx - \omega t + \phi)})\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。

三、不同形式的波动方程之间的关系1. 时间域的波动方程和空间域的波动方程时间域的波动方程和空间域的波动方程在形式上是相似的，都可以表示为简谐波的位移随时间和空间的变化而发生正弦或余弦函数的周期性振荡。

它们之间通过变量的不同而具有不同的物理意义，但是描述的是同一种波动现象。

2. 复数形式的波动方程和实数形式的波动方程在复数形式下，简谐波的波动方程可以更加简洁地描述，通过复数的指数函数形式可以很方便地进行波动的运算和分析。

复数形式的波动方程和实数形式的波动方程是等价的，可以相互转化，但在不同的数学和物理背景下有着不同的应用优势。

四、平面简谐波的应用领域平面简谐波作为一种特殊的波动形式，广泛应用于物理学、工程学、生物学等领域。

它在声学、光学、电磁学、机械振动、信号传输等方面有着重要的应用价值，可以用来描述和分析各种复杂的波动现象。

关于平面波波动方程的推导

关于平面波波动方程的推导

关于平面波波动方程的推导
一．平面波概念
1、平面波是指在某一领域内，波动运动的模式被限制在一个面上，即只具有一个
指向贯穿全域的波动方向的波动模式的称为平面波。

2、当一种介质中的介质振动，且振动波断面是平面时，就可以称为是平面波。

二．平面波波动方程
1、平面波波动方程即它的物理意义，指的是平面内找到各点上时间波速度的模式，当所有的点满足这个模式时，说明振动波断面是平面波。

2、它是一个非常重要的方程，用来描述特定领域内某种波运动模式的变化情况。

它也是一个包含了有关波速、张力系数等重要参数，受这些参数影响影响其形态及特性变化的方程。

三．平面波波动方程的推导
1、平面波波动方程是基于方程即事实来推导的，其主要思路是：先首先考虑可以
根据实验拟合出的线性模型来简化分析问题，再根据它的有限差值表达式，推导出平面波波动方程，就是Lamb导热方程。

2、根据常见维度理论中对Lamb导热方程的推导，由Lamb导热方程可推导出平
面波波动方程。

推导过程中，首先要分析定义波的空间偏微分方程中的压强U的
变化，其次，考虑在单位时间内产生的波的波动性质。

使用创新的振动模型，把压强U区分为正向和负向波，考虑受拉格朗日中值定理的影响，把正向和负向的压
强U的变化反应在波动方程中，通过不断的积分和相关变换，就可以得到平面波
波动方程。

3、最后，根据经验和实验数据，推导出量化参数，也就可以获得局部地区的平面
波波动方程了。

平面波的波动方程

平面波的波动方程

T
dx
t
2
m x
2
m
§17－6 波的能流密度和强度
一、机械波的能流密度
x
设 y A cos(t kx )
o
1 y 2 E k mx ( ) 2 t
y
1 2
u A
B
x
y x x y x 1 1 x 2 2 2 y 1 y E p T x 1 x Tx x x 2
点位移是各个波单独在该点引起的位移的矢量和。
振动叠加发生在单一质点上
波的叠加发生在波的相叠区域 波动方程的线性决定了波服从叠加原理 波的强度过大非线性波 叠加原理不成立 ★电磁波 麦可斯韦方程组的四个方程都是线性的 , 如果 D E和B mH 也是线性关系 ------
1. 演示： Zlcai
2.表达式 设
y1 A cost kx y2 A cost kx
y y1 y2 2 A cos kx cost
y y1 y2 2 A cos kx cost
３. 振幅
kx n
腹－腹
n 0,1,2
x
波腹

2
kx 2n 1
节－节 腹－节

2
n 0,1,2 波节

2
x
x

4
４.相位 作振幅为
2 A cos kx 的简谐振动
两相邻波节之间的质元相位相同
每一波节两侧各质元相位相反
５.能量 波节只有势能，波腹只有动能 当所有各点达到最大位移，全部能量为势能 当所有各点达到平衡位置，全部能量为动能 经1/4T，波节附近势能转化为波腹附近动能
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§17－5 平面波的波动方程 －
各种平面波都满足下列方程
y y =u t x
2 2 2 2 2
称为平面波的波动方程 平面简谐波波动式是它的解
例2
弦上的横波，设线密度 张力T 不变） 弦上的横波，设线密度，张力T（不变）
T
αT
2
T
α
1
T sinα2 T sinα1 ≈ T(tgα2 tgα1 ) 2 y y y y = T dx = dx 2 =T x x x x 2 2 T y T y u= =
y1 = Acos(ωt kx) y2 = Acos(ωt + kx)
y = y1 + y2 = 2 Acos kx cosωt
y = y1 + y2 = 2 Acos kx cosωt
３. 振幅
kx = ±nπ
腹－腹
n = 012L 波腹 ,,
x =

λ
2
kx = ±( 2n +1)
节－节 腹－节
二、波的干涉 １.相干条件 相干条件 频率相同，振动方向相同， 频率相同，振动方向相同，相位差恒定 两相干波在空间相遇， 两相干波在空间相遇，某些点的振动始终加强另一 些点的振动始终减弱，即出现干涉现象。 些点的振动始终减弱，即出现干涉现象。
设 y1 = A cos(ωt +1 kr ) 1 1
3 λ 2
P
解:
Q
R
= 1 2 k(r1 r2 ) 3 = k λ = 3π 减弱 2
A= 0
三、驻波 当两列振幅相同，频率相同， 当两列振幅相同，频率相同，振动方向相同的 波以相反方向传波时，叠加形成驻波 驻波。 波以相反方向传波时，叠加形成驻波。 1. 演示： Zlcai 演示： 2.表达式 表达式 设
2 1
2 1
λ
2
1
r2 r1 = ±nλ, n = 012L ,,
A = A + A2 1
当
2 1
I = I1 + I2 + 2 I1I2 λ r r = ±( 2n +1) , n = 012L ,, 2
I = I1 + I2 2 I1I2
相长
A = A A2 1
相消
例:
两相干机械波，振源相位差π的奇数倍， 两相干机械波，振源相位差π的奇数倍， 点相遇， 在p点相遇，若波程差为半波长的偶数倍 点是加强还是减弱？ 问p点是加强还是减弱？
见Zlcai
O1 r1 P O2 r2
y2 = A2 cos(ωt +2 kr2 ) y = y1 + y2 = Acos(ωt +)
其中
A = A + A2 + 2 A A2 cos 1 1
2 2 2
设 当
= 1 2 k(r1 r2 ) 2π = = k(r r ) = (r r )
2 2 2
E = xω A sin (ωt kx)
单位体积中的机械能 单位体积中的机械能
E 2 2 2 ε= = ρω A sin (ωt kx) Sx
1T 1 2 2 ε = ∫ εdt = ρω A T0 2
二、波的能流密度 波的强度
单位时间内通过截面的波动能量称为能流 单位时间内通过单位垂直截面的波动能量 称为能流密度 称为能流密度
振动叠加发生在单一质点上 波的叠加发生在波的相叠区域 波动方程的线性决定了波服从叠加原理 波的强度过大→ 波的强度过大→非线性波 →叠加原理不成立 ★电磁波 麦可斯韦方程组的四个方程都是线性的 , 如果 r r r r D = εE和 = H 也是线性关系 -----B 解满足叠加原理。 解满足叠加原理。 光波在媒质中传播时 光波在媒质中传播时 弱光 媒质可看作线性媒质 媒质非线性,波的叠加原理不成立 强光 媒质非线性 波的叠加原理不成立
解:
= 1 2 k(r1 r2 )
= ( 2k +1)π
1 2
r1 r2 = 2n
λ
2
∴ = ( 2k +1)π
振动减弱
2π
λ
nλ = ( 2k +1 2n)π
例:
3 设两相干波源P,Q，相同振幅，PQ = λ 设两相干波源 ， 2
R为PQ连线上任一点，求R点振动的振幅 为PQ连线上任一点， 连线上任一点 点振动的振幅
从参考圆可知:φ1=π/3 从参考圆可知
π
3
y
⑵
10 0.5 +10 x π +π y′ = 0.04cos100πt + 2π 3 2 11 = 0.04cos100πt + πx + 6 因波节间距离为λ/2=1m,又x2是节点，所以节点坐标 ⑶因波节间距离为 又 是节点，所以节点坐标: x=0,1,2, …10m 波腹坐标: 波腹坐标 x=0.5,1.5, …9.5m
12
2
单位： 单位：贝尔（bel） ）
1 1dB = bel 10
声波, 超声波， 声波 超声波，次声波
§17－8 波的叠加 波的干涉 －
一、波的叠加原理 １.波的独立性原理 波的独立性原理 几个波源产生的波，在传播过程相遇时 每个波的 几个波源产生的波，在传播过程相遇时,每个波的 波长，频率，振动方向， 波长，频率，振动方向，传播方向都不因其它波 的存在而改变。即各个波相互间没影响， 的存在而改变。即各个波相互间没影响，每个波 的传播就象其单独存在时一样。 的传播就象其单独存在时一样。 ２.波的叠加原理 波的叠加原理 当几列波在媒质中某点相遇时， 当几列波在媒质中某点相遇时，该点的振动是 各个波单独存在时引起该点振动的合振动即该 点位移是各个波单独在该点引起的位移的矢量和。 点位移是各个波单独在该点引起的位移的矢量和。
[
2
2
]
1 2
2
1 y 2 1 y E = Ek + Ep = x( ) + Tx 2 t 2 x
对于平面简谐波
2
1 2 2 2 Ek = xω A sin (ωt kx) 2 1 Ep = Txk 2 A2 sin2 (ωt kx) 2
Qu =
ω
k
=
T
∴Ek = Ep (同步变化)
⑷I=0
2 2 x+dx x
T
dx
t
2
x
2
§17－6 波的能流密度和强度 －
一、机械波的能流密度
x
设 y = Acos(ωt kx)
o
1 y 2 Ek = x( ) 2 t
y
1 2
u A
B
x
y x → ( x) + ( y) = x1+ 1 x 2 2 2 1 y Ep = Tx1+ x ≈ Tx y x x 2
u
S
r r J = εu
波的强度
1T uT I = J = ∫ Jdt = ∫ εdt = uε T0 T0
对于平面简谐波
1 2 2 I = ρω A u 2
SI : W m
2
球面简谐波的波动式： 球面简谐波的波动式：
1 2 2 I1 = ρA ω u 1 2
r1 r2 o
1 2 2 I2 = ρA2 ω u 2
π
2
n = 012L 波节 ,,
λ
2
x =
x =
λ
4
４.相位 相位 作振幅为
2 A cos kx 的简谐振动
两相邻波节之间的质元相位相同 每一波节两侧各质元相位相反 ５.能量 能量 波节只有势能， 波节只有势能，波腹只有动能 当所有各点达到最大位移， 当所有各点达到最大位移，全部能量为势能 当所有各点达到平衡位置， 当所有各点达到平衡位置，全部能量为动能 经1/4T，波节附近势能转化为波腹附近动能 ，
在无吸收时,通过两球面的能流相等 在无吸收时 通过两球面的能流相等
I14πr1
2=I
24πr2
2
A r 1 = 2 A r 2 1
A y = 0 cos(ωt kr) r
三、声波 频率范围 声强级
声强级
20 20000Hz
I L = log I0
分贝(dB） ） 分贝
I0 = 10 W / m
2
解:⑴波速 ⑴
10 = =100m u= 3 s 10
F
波长
u 100 λ= = = 2m ν 50
π
3
x x1 y = Acos2πν +φ1 2π t λ x 0.5 π = 0.04cos100πt + 2π 3 2 5 = 0.04cos100πt πx + π 6
四、简正模式 两端固定的张紧弦中产生驻波
n
λ
2
=L
n = 12,3 , L
nu υ= = λ 2L
u
n =1,2,3 L 简正频率
对应的驻波称为弦的简正模或 对应的驻波称为弦的简正模或固有振动 简正模
n=1
n=2
例、如图所示，在一根线密度=10－3kg/m和张力 如图所示，在一根线密度 和张力 F=10N的弦线上 沿x轴正方向传播简谐横波 其频率 的弦线上,沿 轴正方向传播简谐横波 轴正方向传播简谐横波,其频率 的弦线上 ν=50Hz,振幅 振幅A=0.04m。巳知弦线上离坐标原点 振幅 。 处的质点在t=0时刻的位移为 且沿y轴 X1=0.5m处的质点在 时刻的位移为 A ,且沿 轴 处的质点在 时刻的位移为+ 且沿 2 负向运动,当波传播到 当波传播到x 处固定端时,被全部反 负向运动 当波传播到 2=10m处固定端时 被全部反 处固定端时 试写出: 射。试写出 入射波的波动方程; ⑴入射波的波动方程 反射波的波动方程; ⑵反射波的波动方程 y ⑶入射波与反射波叠加的 u 合成波在0≤x≤10m区间 合成波在 区间 内各波节和波腹处的坐标; 内各波节和波腹处的坐标 合成波的平均能流密度。 ⑷合成波的平均能流密度。 . x .1 o x x