下载文档原格式
波动方程的简谐平面波解在建立了波动方程之后，我们来讨论其解的形式及其特性。
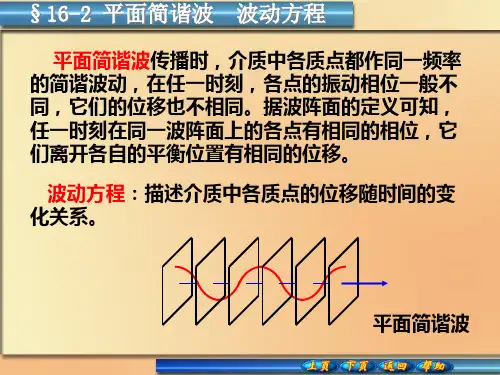
1、 简谐平面波（1）波动方程的简谐平面波解声波在空间中传播，其传播方向和波阵面垂直。
平面波是波阵面是平面的声波，而简谐平面波是波阵面（对简谐波而言，波阵面也是等相位面）是平面的简谐声波。
具有任意波形的声波可以通过付里叶变换分解为多个具有不同频率的简谐平面波的叠加。
因此，简谐波传播是波动传播的基础。
一般简谐平面波的声压幅值在等相面上有一定的分布。
这里只讨论声压幅值在等相面上处处相同（均匀平面波）的简单情况，较为复杂的非等声压幅值平面波（非均匀平面波）在后面的学习中会遇到。
对一维均匀简谐平面波，声压幅值可以只用一个坐标来描述。
若取平面波的传播方向为x 轴正方向，假设波动方程中c 为常数，则波动方程的均匀简谐平面波解可以分离变量有如下形式：(,)()()p x t p x T t =，(2-23) 其中，()p x 和()T t 分别为(,)p x t 的空间坐标相关因子和时间相关因子。
将(2-23)式代入到 (2-15)中，并分离变量，得2222221()()()()d T t c d p x T t dt p x dtω==-， (2-24) 其中，2ω-为分离常数。
由(2-24)式可得两个方程：222()()0d T t T t dtω+=， (2-25) 222()()0d p x k p x dt+=。
(2-26) 其中，222k c ω=，为常数。
(2-25)式的两个特解为j t e ω和()j t e ω-，后者描述具有“负频率”的振动，无实际意义，只保留j t e ω；(2-26) 式的两个特解为jkx e 和jkx e -。
由此得到波动方程的简谐平面波解为j[t-kx]j[t+kx](,)(,)(,) =Aeep x t p x t p x t B ωω+-=++ 。
(2-27)对推导过程中几个量物理意义的讨论：① 由(2-25)的解j t e ω可以看出，ω是简谐波的圆频率，也可以理解为：在简谐波传播的过程中，介质中某一质点经过单位时间变化的相位值(对应着周期数)。
第2章波函数和薛定谔方程既然辐射和粒子都具有波动性和微粒性，那么，如何理解这两属性呢？它们如何统一起来？ 经典物理观点必须被修改。
主要表现：a. 波－粒两象性P （粒子） ν λ （波）ω=ν= h E （Planck 假设）Einstein 关系k P = （P h =λ，λπ=2k ） （de Broglie 假设） de Broglie 关系 ∴ 具有确定动量的自由粒子被一平面波所描述)Et r P (i )t r k (i AAe-⋅ω-⋅==ψb. 物理量取值不一定是连续的辐射体辐射的能量取值 ν=nh E ,2,1,0n = 氢原子的能量202n 8n a eE πε⋅-=cm 10529.0em 4a 82e 200-⋅=πε=由于平常粒子的波长1010-<λÅ，所以观察不到干涉, 衍射现象。
微观粒子，如电子1≈λÅ，因此在原子线度下可能显示出波动性。
而在宏观测量尺度下，几乎也不显示波动性。
将粒子所具有的微粒性和波动性统一起来，这在经典物理学中看来是不可能的，因经典粒子 经典波√原子性（整体性） ⨯实在物理量的空间分布 ⨯轨道 √干涉，衍射这两者是不相容的。
描述微观粒子既不能用经典粒子，也不能用经典波，当然也不能用经典粒子和经典波来描述。
§1 波函数的统计解释一、波函数的引入描述自由粒子可用平面波波函数)(Et r p ipAe -⋅=ψ来描述。
如果粒子处于随时间和位置变化的力场中运动，这样的微观粒子的运动状态也可以用较复杂的波(,)r t ψ完全描述。
二、波函数的解释1、经典物理学中粒子与波的有关概念经典概念中粒子意味着： 1.有一定质量、电荷等“颗粒性”的属性;2．有确定的运动轨道，每一时刻有一定位置和速度。
经典概念中波意味着：1. 某种实在的物理量的空间分布作周期性的变化; 2．干涉、衍射现象，即相干叠加性。
2、对波粒二象性的两种错误的看法 (1). 波由粒子组成波是由粒子组成的，把波看成是由大量粒子相互作用而在空间形成的一种疏密相间的周期分布。
