直线插补

多轴联动常用插补算法
多轴联动是指在数控加工过程中，多个轴同时协同运动以完成复杂零件的加工。

为了实现精确且高效的多轴联动，需要采用合适的插补算法进行控制。

常见的多轴联动插补算法包括以下几种：
1. 直线插补：直线插补是最基本的插补算法，用于控制轴在直线轨迹上运动。

直线插补算法根据预设的轨迹，通过控制电机转速和加速度，使轴按照指定的速度和加速度曲线运动。

2. 圆弧插补：圆弧插补用于控制轴在圆弧轨迹上运动。

与直线插补类似，圆弧插补算法也需要根据预设的轨迹，控制电机转速和加速度，使轴按照指定的速度和加速度曲线运动。

3. 样条插补：样条插补是一种基于多项式的插补方法，可以实现较为复杂的曲线轨迹。

通过拟合多项式曲线，样条插补可以控制轴在不同坐标系下实现平滑过渡，提高加工精度。

4. 电子凸轮插补：电子凸轮插补是一种基于数字信号处理的插补方法，通过预设的数字信号序列来控制轴的运动。

电子凸轮插补可以实现复杂的轨迹和动作，但相对于其他插补算法，其精度较低。

5. 全闭环运动控制插补：全闭环运动控制插补是一种基于反馈控制的插补方法，通过对各轴实际位置与电机实际位置之间的偏差进行实时调整，实现高精度的多轴联动。

全闭环运动控制插补可以保证多轴联动轮廓精度、定位精度及重复定位精度，同时保证伺服电机稳定运行。

在实际应用中，根据不同的加工需求和设备条件，可以选择合适的插补算法来实现多轴联动。

同时，为了提高插补算法的性能和稳定性，还可以采用诸如优化算法、PID控制等方
法进行优化。

数控机床直线插补公式数控机床直线插补是数控机床加工过程中最基本的插补方式之一。

它通过控制机床的各轴运动，使切削工具按照一定的轨迹进行直线运动，实现对工件的加工。

直线插补是数控机床实现高速、高精度加工的关键技术之一。

首先，直线插补的数学模型是线性插补方程。

设机床坐标系为Oxyz，工件坐标系为OXYz，设直线的起点为P1(x1, y1, z1)，终点为P2(x2, y2, z2)。

则直线插补方程可以表示为：x=x1+(x2-x1)*t；y=y1+(y2-y1)*t；z=z1+(z2-z1)*t，其中t为时间参数，取值范围为[0,1]。

通过控制t的变化，可以实现直线插补运动。

其次，直线插补的速度规划是实现高速加工的关键。

直线插补过程中，速度的规划要考虑到工件形状、机床的动态特性和加工精度要求等因素。

一般来说，直线插补速度规划可以分为两个阶段：加速段和匀速段。

加速段的目的是使机床迅速加速到设定的速度，而匀速段则是保持恒定的速度进行加工。

速度规划的目标是使机床在考虑动态特性和加工精度要求的前提下，尽可能地提高加工效率。

同时，直线插补的误差补偿是保证加工精度的关键。

由于机床本身的误差和外部环境的影响，直线插补过程中会产生一定的误差。

为了保证加工精度，需要对误差进行补偿。

误差补偿一般分为两类：静态误差补偿和动态误差补偿。

静态误差补偿是在刀具轨迹上对误差进行修正，常用的方法有坐标误差补偿、用户自定义的曲线修正等；而动态误差补偿是通过改变刀具轨迹，使得误差在加工过程中得以消除，常用的方法有加速度预测和最优轨迹规划等。

最后，直线插补的应用范围非常广泛。

它适用于各种形状的工件加工，如直线、圆弧、椭圆等。

在汽车制造、航空航天、电子设备等行业中，直线插补广泛应用于零件的加工。

直线插补可以实现高速加工和高精度加工，大大提高了生产效率和产品质量。

总结起来，数控机床直线插补是实现高速、高精度加工的重要技术。

它通过控制机床轴的运动，使切削工具按照一定的轨迹进行直线运动，从而实现对工件的加工。

数字积分插补法的直线插补误差数字积分插补法是现代数控技术中的重要方法之一。

具体来说，它是通过对给定的曲线信息进行处理，得到一系列机床控制指令，在保证加工精度和效率的同时，实现曲线的准确加工。

然而，在数字积分插补法中，由于其数值计算的本质和机床的机械特性，直线插补误差是无法避免的。

本文将探讨数字积分插补法的直线插补误差，包括其成因、影响因素、解决方法等内容，旨在为制造业相关从业者提供一定的参考和指导。

1.直线插补误差的成因直线插补误差是数字积分插补法中常见的问题之一，其主要成因包括以下几个方面：1）数值计算误差：数字积分插补法是通过对给定的曲线信息进行插值得到指令进行控制，其中涉及到大量的数值计算。

由于计算机计算精度等方面的局限性，数值计算的精度和误差会影响到插补结果的准确性。

2）机床动态特性：机床本身具有一定的刚度、质量以及振动等动态特性，这些特性会导致机床加工时出现一定的误差。

尤其在高速运动和高精度加工时，机床的动态特性和误差更加明显。

3）刀具和工件特性：刀具和工件的特性直接影响到机床加工的准确性，例如刀具磨损、工件变形等都会导致加工误差的发生。

2.直线插补误差的影响因素直线插补误差的大小与许多因素有关，主要包括以下几点：1）直线段的长度和方向：直线段的长度和方向决定了机床加工时所需的时间和加工路线，从而影响插补的起始和终止点以及运动轨迹。

2）机床加工速度和精度：机床加工速度和精度直接决定了加工的渐进过程和目标精度。

对于运动速度和加工精度要求高的工件，直线插补误差影响更大。

3）刀具磨损和工件变形：刀具磨损和工件变形会导致机床加工的实际轮廓和理论轮廓不一致，从而影响插补结果的准确性。

4）数值计算方法和误差分析：数值计算方法和误差分析技术对插补结果的精度和准确性影响很大。

3.直线插补误差的解决方法针对直线插补误差的影响因素，我们可以采取一些解决方法来尽可能地减小误差，这些方法包括以下几个方面：1）数值计算方法的改进：通过提高计算精度和准确度等方式改进数值计算方法，可以减小误差。

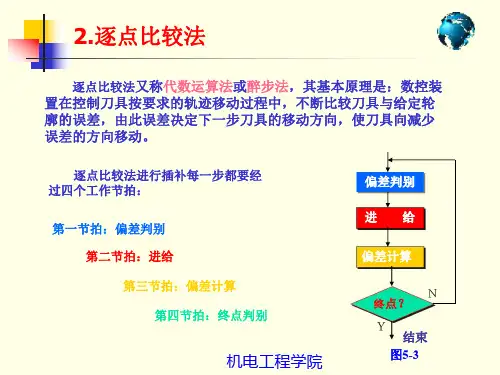
§2—1 逐点比较法逐点比较法是我国数控机床中广泛采用的一种插补方法，它能实现直线、圆弧和非圆二次曲线的插补，插补精度较高。

逐点比较法，顾名思义，就是每走一步都要将加工点的瞬时坐标同规定的图形轨迹相比较，判断其偏差，然后决定下一步的走向，如果加工点走到图形外面去了，那么下一步就要向图形里面走；如果加工点在图形里面，那么下一步就要向图形外面走，以缩小偏差。

这样就能得出一个非常接近规定图形的轨迹，最大偏差不超过一个脉冲当量。

在逐点比较法中，每进给一步都须要进行偏差判别、坐标进给、新偏差计算和终点比较四个节拍。

下面分别介绍逐点比较法直线插补和圆弧插补的原理。

一、 逐点比较法直线插补如上所述，偏差计算是逐点比较法关键的一步。

下面以第Ⅰ象限直线为例导出其偏差计算公式。

图 2-1 直 线 差 补 过 程e )OY图2-1 直线插补过程点击进入动画观看逐点比较法直线插补如图2—1所示，假定直线 OA 的起点为坐标原点，终点A 的坐标为e e i j A(x ,y ),P(x ,y )为加工点，若P 点正好处在直线OA 上，那么下式成立：e j i e x y - x y 0若任意点i j P(x ,y )在直线 OA 的上方（严格地说，在直线OA 与y 轴所成夹角区域内），那么有下述关系成立：jei ey y x x >亦即:e j i e x y - x y 0>由此可以取偏差判别函数ij F 为：ij e j i e F x y - x y ＝由 ij F 的数值（称为“偏差”）就可以判别出P 点与直线的相对位置。

即： 当 ij F =0时，点i j P(x ,y )正好落在直线上；当 ij F >0时，点i j P(x ,y )落在直线的上方；当ij F <0时，点i j P(x ,y )落在直线的下方。

从图2—1看出，对于起点在原点，终点为A （ e e x ,y ）的第Ⅰ象限直线OA 来说，当点P 在直线上方（即ij F >0）时，应该向+x 方向发一个脉冲，使机床刀具向+x 方向前进一步，以接近该直线；当点P 在直线下方（即ij F <0）时，应该向+y 方向发一个脉冲，使机床刀具向+y 方向前进一步，趋向该直线；当点P 正好在直线上（即 ij F =0）时，既可向+x 方向发一脉冲，也可向+y 方向发一脉冲。

直线插补计算过程步骤
一。

直线插补这事儿，简单来说，就是在给定的两点之间，算出中间那些点的坐标，让运动轨迹能连成一条直线。

1.1 首先得明确起点和终点的坐标，这就好比你要知道从哪儿出发，到哪儿结束。

这俩坐标就是整个计算的基础，可马虎不得。

1.2 然后根据起点和终点，算出直线的斜率。

这斜率就像是路的坡度，决定了运动的方向和倾斜程度。

二。

接下来就是关键的计算步骤啦。

2.1 把整个直线分成好多小段，每一小段的长度得根据精度要求来定。

这就像切蛋糕，想切得细点儿，段数就得多。

2.2 按照设定的小段长度，根据斜率和起点坐标，依次算出每个小段终点的坐标。

这就像是一步一个脚印，稳稳地往前走。

2.3 不断重复这个过程，直到接近或者到达终点坐标。

这中间可不能出错，不然这直线就走歪啦。

三。

把算出来的这些点连起来，那就是咱们想要的直线插补轨迹。

3.1 实际应用中，还得考虑速度、加速度这些因素，让运动更平稳、更高效。

3.2 直线插补在数控加工、机器人控制等领域那可是大有用处，能让设备精确地按照咱们的想法工作。

直线插补计算虽然有点复杂，但只要咱理清思路，一步一步来，就能把这事儿搞定，让机器乖乖听话，干出漂亮活儿！。

直线插补两轴速度的算法直线插补是数控系统中常用的一种插补方式，用于控制机床在直线轨迹上运动。

两轴速度算法主要是为了实现机床在直线轨迹上的平滑运动，保证加速度和减速度的均匀分布，从而提高机床的运动性能和加工质量。

下面将介绍一种经典的直线插补两轴速度算法：S型加减速算法。

S型加减速算法主要分为三个阶段：加速阶段、匀速阶段和减速阶段。

其中，加速阶段和减速阶段的运动速度是不断变化的，而匀速阶段的运动速度是恒定的。

1.加速阶段：在此阶段内，机床的速度逐渐增加，加速度保持不变。

加速度的大小可以根据所设定的加速时间和运动距离来计算。

算法的基本思路是通过改变步进值的大小来控制速度的增加。

具体计算方式为：在加速阶段，速度的增加量等于加速度与步进值之间的差值。

2.匀速阶段：当机床的速度达到所设定的匀速值后，进入匀速阶段。

在此阶段内，机床的速度保持不变，即步进值保持不变。

3.减速阶段：当机床接近目标位置时，需要减速停止，进入减速阶段。

在此阶段内，速度逐渐减小，减速度保持不变。

减速阶段的步进值计算方式与加速阶段相同，只是步进值的增加量为减速度与步进值之间的差值。

在整个插补过程中，需要根据机床的运动性能和加工要求来确定加速度、减速度和匀速值的大小。

一般来说，加速度和减速度较大，可以提高机床的加工效率，但是会增加机床的振动和冲击力，影响加工质量；加速度和减速度较小，可以减少机床的振动和冲击力，提高加工质量，但是会降低机床的加工效率。

除了S型加减速算法，还有其他的直线插补两轴速度算法，如梯形加减速算法、指数加减速算法等。

每种算法都有自己的特点和适用范围，可以根据具体的应用需求来选择合适的算法。

总之，直线插补两轴速度算法是数控系统中的重要内容，对于提高机床的运动性能和加工质量具有重要意义。

希望以上内容对您有所帮助。

如有更多疑问，请随时提问。