直线插补与圆弧插补程序设计

实验一工作台直线插补运动1 实验目的1.了解工作台直线插补原理和算法；2.在掌握直线插补原理的基础上实现平面绘图。

2 实验设备1.直线／旋转工作台；2.工作台控制箱一台；3.笔架夹持器、画笔及画板。

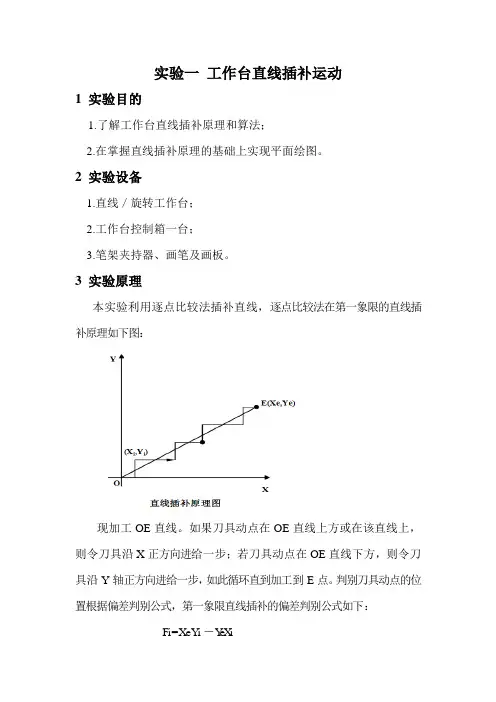
3 实验原理本实验利用逐点比较法插补直线，逐点比较法在第一象限的直线插补原理如下图：现加工OE直线。

如果刀具动点在OE直线上方或在该直线上，则令刀具沿X正方向进给一步；若刀具动点在OE直线下方，则令刀具沿Y轴正方向进给一步，如此循环直到加工到E点。

判别刀具动点的位置根据偏差判别公式，第一象限直线插补的偏差判别公式如下：Fi = Xe Y i －Y e X iFi≥0时，偏差判别公式为F i+1=F i -Ye 向X正方向进给Fi<0时，偏差判别公式为F i+1= F i＋Xe，向Y正方向进给逐点比较法插补节拍：逐点比较法插补需要四个节拍，即偏差判别、进给、偏差计算和终点判别。

4.4 实验步骤1.按使用说明书上将工作台组合成二自由度直线工作台，安装好笔架夹持器，放置好画板，并正确连接电缆。

2.安装上笔架夹持器及画笔，在桌面相应位置放好画板，使笔尖接触到画板；3.接通控制箱电源；4.启动计算机，运行工作台控制软件；5.在“工作台组合方式”界面中选择X直线工作台和Y直线工作台；6.单击主界面“工作台复位”按钮，工作台进行回零运动，运动完成后工作台处于零点位置；7.把画笔安装到笔架夹持器上，使笔尖接触到画板；8.单击“直线插补”按钮；9.加速方式选择“梯形”，插补目标X轴填写0，Y轴填写-30，点击“运动”按钮，画出一条直线，10.插补目标X轴填写30，Y轴填写30，点击“运动”，11.插补目标X轴填写30，Y轴填写0，点击“运动”，12.插补目标X轴填写0， Y轴填写0，点击“运动”，13.几条直线在画板上组成一个梯形，14.单击“工作台复位”按钮，使工作台回到零点位置；15.关闭计算机；16.断开控制箱电源。

直线插补与圆弧插补程序设计一．直线插补1.直线插补程序流程图直线插补程序流程图2.直线插补程序设计#include <stdio.h>#include <graphics.h>#include <stdlib.h>void cb_line(int x1, int y1, int x2, int y2) {int dx, dy, n, k, i, f;int x, y;dx = abs(x2-x1);dy = abs(y2-y1);n = dx + dy;if (x2 >= x1) {k = y2 >= y1 ? 1: 4;x = x1;y = y1;} else {k = y2 >= y1 ? 2: 3;x = x2;y = y2;}putpixel(x, y, 1);for (i = 0, f = 0; i < n; i++)if (f >= 0)switch (k) {case 1:putpixel(x++, y, 1);f -= dy;break;case 2:putpixel(x, y++, 1);f -= dx;break;case 3:putpixel(x--, y, 1);f -= dy;break;case 4:putpixel(x, y--, 1);f -= dx;break;}elseswitch (k) {case 1:putpixel(x, y++, 1);f += dx;break;case 2:putpixel(x--, y, 1);f += dy;break;case 3:putpixel(x, y--, 1);f += dx;break;case 4:putpixel(x++, y, 1);f += dy;break;}}int main(){cb_line(0,0,15,20); /* <--- you forgot ; here */return 0;}二.圆弧插补2.1.四象限圆弧插补程序流程图2.1四象限圆弧插补程序设计#include <stdio.h>#include <math.h>int ArcXY(double dfx0,double dfy0,double dfrx, double dfry,int angle); int symbol(double number);main(){ArcXY(0,0,-3,5,360);getch();}int ArcXY(double dfx0,double dfy0,double dfrx, double dfry,int angle) {FILE *f1;double i,j,dx,dy,dfr,x,y,ang,step,f = 0.01;int flag,tempx,tempy,statex,statey,direction = 1;dfr = sqrt((dfrx - dfx0) * (dfrx - dfx0) + (dfry - dfy0) * (dfry - dfy0));if(dfx0 == 0){dfx0 = 1;dfrx = dfrx + 1;statex =1;}if(dfy0 == 0){dfy0 = 1;dfry = dfry + 1;statey =1;}dfrx = 2 * dfx0 - dfrx;i = dfx0 - dfrx;j = dfy0 - dfry;x = dfx0 ;y = dfy0 ;step = ang = 180 * 2 * asin(f/(2*dfr))/3.1415926;if(((dfx0 > 0) && (dfy0 > 0)) || ((dfx0 < 0) && (dfy0 < 0))){flag = direction;}if(((dfx0 < 0) && (dfy0 > 0)) || ((dfx0 > 0) && (dfy0 < 0))) {flag = -direction;}f1=fopen("c:\\c.txt","w+");if(statex ==1){x = x - 1;}if(statey ==1){y = y - 1;}fprintf(f1,"%f,",x);fprintf(f1,"%f\n",y);while(ang < angle){dx = f * (j + flag*(f * i)/(2 * dfr))/dfr;dy = f * (i - flag*(f * j)/(2 * dfr))/dfr;tempx = symbol(x);tempy = symbol(y);x = x + dx;y = y + dy;fprintf(f1,"%f,",x);fprintf(f1,"%f\n",y);if( (tempx !=symbol(x)) || (tempy != symbol(y)) ){flag = -flag;}i = i - dx;j = j + dy;ang = ang + step;}return 0;}int symbol(double number) {if(number > 0){return 1;}else{return -1;}}。

实验三数控插补原理与实现一、实验目的（1）了解直线插补、圆弧插补原理和实现方法。

（2）利用运动控制器基本控制指令实现直线插补和圆弧插补。

（3）掌握运动控制卡的编程方法。

二、实验设备（1）两维直线运动数控教学实验系统一套。

（2） MPC02运动控制卡一块。

（3）辅助设备：台式计算机一台，安装Windows 98或以上操作系统，安装VC++ 或VB 开发环境。

三、实验内容根据插补计算原理，利用运动控制器基本位臵控制指令，在VC++或VB环境下编写插补程序，并在X-Y平台上进行验证。

四、实验步骤1. 直线插补根据逐点比较法直线插补原理进行编程，然后编译运行，并按图2.6给定坐标进行实验，观察画笔运动轨迹是否如图2.6所示。

图2.6 直线插补运动轨迹设有一工件，其廓形为三角形。

建立工件X-Y坐标系如图2.6所示。

以点A为坐标原点，则点1的坐标为(20, 0)，点2的坐标为(45, 50)，点3的坐标为(70, 0)。

设在X-Y运动平台归零时，画笔在A点。

此时，X-Y运动平台的坐标系与工件坐标系是一致的。

画笔运动轨迹如图2.6所示。

2. 圆弧插补根据逐点比较法圆弧插补原理进行编程，并编译运行。

按图2.7给定坐标进行实验，观察画笔运动轨迹是否如图2.7所示。

图2.7 圆弧插补运动轨迹设有一工件，如图 2.7所示，其廓形曲线由两段圆弧组成，两段圆弧半径分别为40和20。

设在X-Y运动平台归零时，画笔在A点。

在X-Y运动平台坐标系中，坐标原点在A点。

工件上的1、2、3点坐标分别为：点1(0,15)、点2(40,15)、点3(60,15)。

画笔运动轨迹如图2.7所示。

五、实验总结（1）简述常见的插补算法。

（2）根据实验分析逐点插补算法的精度和局限性。

实验五数控代码编程一、实验目的了解从运动控制器的基本控制指令到数控代码库的实现过程。

二、实验设备（1）两维直线运动数控教学实验系统，三维直线运动数控铣教学实验系统各一套。

数控系统中直线与圆弧插补算法的探讨导言数控系统是一种广泛应用于机械加工领域的自动化控制系统。

其中，直线与圆弧插补算法是数控系统中的核心算法之一。

本文将深入探讨直线与圆弧插补算法的原理、方法以及应用。

直线插补算法直线插补是数控系统中最基本的插补运动方式之一。

它的目标是实现两个给定点之间的直线路径。

在直线插补算法中，我们需要考虑以下几个方面：1.起始点和终点的坐标：为了实现直线插补，我们需要明确起始点和终点的空间坐标。

2.运动速度和加速度：直线插补需要考虑加速度和速度的变化，以实现平滑而又快速的运动。

3.插补精度：直线插补的精度决定了运动轨迹的平滑度和误差控制的能力。

直线插补算法的基本思路是将插补路径划分为多个小段，然后通过控制每个小段的加速度和速度，以达到平滑运动的效果。

常用的直线插补算法包括线性插补算法和B样条插补算法。

线性插补算法线性插补算法是最简单和最基础的直线插补算法之一。

它假设插补路径是一条直线，并根据起始点和终点的坐标以及插补周期，计算出每个插补周期点的位置。

线性插补算法的优点是计算简单，实现容易，但缺点是对于曲线路径的插补效果较差。

B样条插补算法B样条插补算法是一种基于样条曲线的插补算法。

在B样条插补算法中，我们将插补路径表示为一条样条曲线，并通过控制样条曲线的控制点来实现运动轨迹的控制。

B样条插补算法的优点是对曲线路径的插补效果较好，但是计算复杂度较高。

圆弧插补算法除了直线插补，圆弧插补算法也是数控系统中常用的插补方式之一。

圆弧插补用于实现两个给定点之间的圆弧路径。

与直线插补类似，圆弧插补算法也需要考虑起始点和终点的坐标、运动速度和加速度等因素。

圆弧插补算法的基本思路是通过指定起始点、终点和圆心，计算出圆弧路径上每个插补点的位置。

常用的圆弧插补算法包括圆心法和半径法。

圆心法圆心法是一种基于圆心坐标的圆弧插补算法。

在圆心法中，我们通过指定起始点、终点和圆心的坐标，计算出圆弧路径上每个插补点的位置。

数控系统中直线与圆弧插补算法的探讨
数控系统中直线与圆弧插补算法的探讨
数控系统是现代制造业中不可或缺的一部分，它的主要功能是将数字
化的指令转化为机器能够理解的运动控制信号，从而实现对机器的精
确控制。

在数控系统中，直线与圆弧插补算法是非常重要的一部分，
它们决定了机器在加工过程中的精度和效率。

直线插补算法是数控系统中最简单的插补算法之一，它的原理是将直
线分割成若干个小段，然后通过控制机器在每个小段上的运动来实现
整条直线的加工。

在实际应用中，直线插补算法的精度和效率都非常高，因此被广泛应用于各种数控加工设备中。

与直线插补算法相比，圆弧插补算法则更加复杂。

圆弧插补算法的原
理是将圆弧分割成若干个小段，然后通过控制机器在每个小段上的运
动来实现整个圆弧的加工。

在实际应用中，圆弧插补算法的精度和效
率都非常高，但是由于其复杂性，需要更高的计算能力和更复杂的控
制算法来实现。

在实际应用中，直线和圆弧插补算法经常会同时使用。

例如，在加工
一个复杂的零件时，可能需要使用直线插补算法来加工一些直线部分，
而使用圆弧插补算法来加工一些曲线部分。

在这种情况下，数控系统需要能够自动切换不同的插补算法，并且保证整个加工过程的精度和效率。

总的来说，直线和圆弧插补算法是数控系统中非常重要的一部分，它们决定了机器在加工过程中的精度和效率。

在实际应用中，直线和圆弧插补算法经常会同时使用，数控系统需要能够自动切换不同的插补算法，并且保证整个加工过程的精度和效率。

逐点比较法第一象限直线，圆弧插补编程逐点比较法是以折线来逼近给定的轨迹，就是每走一步控制系统都要将加工点与给定的图形轨迹相比较，以决定下一步进给的方向，使之逼近加工轨迹。

逐点比较法以折线来逼近直线或圆弧，其最大的偏差不超过一个最小设定单位。

只要将脉冲当量取得足够小，就可以达到精度要求。

逐点比较插补法在脉冲当量为0.01mm，系统进给速度小于3000mm/min时，能很好的满足要求。

一、逐点比较法直线插补如下图所示设直线 oA 为第一象限的直线，起点为坐标原点o (0 ， 0) ，终点坐标为， A( ) ， P() 为加工点。

若 P 点正好处在直线 oA 上，由相似三角形关系则有即点在直线 oA 上方 ( 严格为直线 oA 与 y 轴正向所包围的区域 ) ，则有即若 P 点在直线 oA 下方 ( 严格为直线 oA 与 x 轴正向所包围的区域 ) ，则有图 3 — 1 逐点比较法第一象限直线插补即令则有：①如，则点 P 在直线 oA 上，既可向 +x 方向进给一步，也可向 +y 方向进给一步；②如，则点 P 在直线 oA 上方，应向 +x 方向进给一步，以逼近oA 直线；③如，则点 P 在直线 oA 下方，应向 +y 方向进给一步，以逼近 oA 直线一般将及视为一类情况，即时，都向 +x 方向进给一步。

当两方向所走的步数与终点坐标相等时，停止插补。

这即逐点比较法直线插补的原理。

对第一象限直线 oA 从起点 ( 即坐标原点 ) 出发，当 F 时， +x 向走一步；当 F<0 时，y 向走一步。

特点：每一步都需计算偏差，这样的计算比较麻烦。

递推的方法计算偏差：每走一步后新的加工点的偏差用前一点的加工偏差递推出来。

采用递推方法，必须知道开始加工点的偏差，而开始加工点正是直线的起点，故。

下面推导其递推公式。

设在加工点 P( ) 处，，则应沿 +x 方向进给一步，此时新加工点的坐标值为新加工点的偏差为即若在加工点 P( ) 处，，则应沿 +y 方向进给一步，此时新加工点的坐标值为，新加工点的偏差为即综上所述，逐点比较法直线插补每走一步都要完成四个步骤 ( 节拍 ) ，即：(1) 位置判别根据偏差值大于零、等于零、小于零确定当前加工点的位置。

数控技术第三次作业题目【1】：第一象限的逆圆插补。

1.取该圆弧的圆心坐标为（0，0），起点坐标为（4，0），终点坐标为（0，4），圆弧半径为4.2.采用逐点比较法的C程序如#include <stdio.h>void main(){int n=8,x,y,f,g;scanf("%d,%d",&x,&y);f=x^2+y^2-16;if (f>=0)g=f-2x+1,x--,n--;printf("%d,%d,%d\n",x,y,n);elseg=f+2y+1,y++,n--;printf("%d,%d,%d\n",x,y,n);if (g>=0)g=g-2x+1,x--,n--;printf("%d,%d,%d\n",x,y,n);elseg=g+2y+1,y++,n--;printf("%d,%d,%d\n",x,y,n);while (n==0)printf("it is over");}3.程序流程图如下：4.程序运行后得到一系列插补点，连接插补点得到插补轨迹如下图所示：5.综上，第一象限的逆圆采用逐点插补法的插补过程及其解决算法如上所述。

题目【2】：第一象限的直线插补取第一象限的直线方程为Y=X，起点坐标为原点（0，0），终点坐标为（4，4）。

1．基于MATLAB的插补程序如下：Xe = input('输入终点横坐标X\nXe = ');Ye = input('输入终点纵坐标Y\nYe = ');h = input('输入步长\nh = ');Tstep= (abs(Xe)+abs(Ye))/h;Step=0;F=0;Xi=0;Yi=0;x = 0;y = 0;Xi=Xi+h; x = [x Xi]; y = [y Yi];endStep=1;while (Step<Tstep)F=Xe*Yi-Xi*Ye;if (F>=0)Xi=Xi+h;elseYi=Yi+h;endx = [x Xi];y = [y Yi];Step = Step+1;hold onendplot(x,y)2.MATLAB程序运行得到的插补图形及其轨迹如下图：综上，用逐点比较法完成了第一象限的逆圆插补和直线插补。

C语言模拟直线插补与圆弧插补程序设计(总17页)-本页仅作为预览文档封面，使用时请删除本页-数控技术课程设计说明书设计题目直线插补与圆弧插补程序设计机械设计以及自动化专业机械工程学院机械102班设计者青岛理工大学 2013年6月20日目录1.设计题目 (1)2.目录 (2)3.直线插补流程图 (3)4.直线插补程序 (4)5.程序结果 (8)6.圆弧插补流程图 (9)7.圆弧插补程序 (10)8.程序结果 (21)一．直线插补1.直线插补程序流程图2.直线插补程序设计#include ""int i,X,Y,X0,Y0,Xe,Ye,F,N;int a[30][2];void main(){int m;int menu();void yi();void er();void san();void si();void te();void shuchu();m=menu();a[0][0]=X0;a[0][1]=Y0;switch(m){case 1:yi();shuchu();break;case 2:er();shuchu();break;case 3:san();shuchu();break;case 4:si();shuchu();break;case 5:te();shuchu();break;default:printf("无法插补\n");}}int menu(){int t;printf("输入起点坐标\n");scanf("%d,%d",&X0,&Y0);printf("输入终点坐标\n");scanf("%d,%d",&Xe,&Ye);if (Xe>=X0&&Ye>=Y0)t=1;else if (Xe<=X0&&Ye>=Y0)t=2;else if (Xe<=X0&&Ye<=Y0)t=3;else if (Xe>=X0&&Ye<=Y0)t=4;else if (Xe==X0&&((Ye>Y0&&Y0>=0)||(Ye<Y0&&Y<=0))) t=5;elset=6;return(t); }void yi(){F=0;N=Xe-X0+Ye-Y0; X=X0;Y=Y0;for(i=1;i<=N;i++) { if(F>=0){X++;a[i][0]=X;a[i][1]=Y;F-=Ye-Y0;}else{Y++;a[i][0]=X;a[i][1]=Y;F+=Xe-X0;}}}void er(){F=0;N=X0-Xe+Ye-Y0; X=X0;Y=Y0;for(i=1;i<=N;i++) {if(F>=0){ X--;a[i][0]=X;a[i][1]=Y;F-=Ye-Y0;}else{Y++;a[i][0]=X;a[i][1]=Y;F+=X0-Xe;}}}void san(){F=0;N=X0-Xe+Y0-Ye; X=X0;Y=Y0;for(i=1;i<=N;i++) {if(F>=0){X--;a[i][0]=X;a[i][1]=Y;F-=Y0-Ye;}else{Y--;a[i][0]=X;a[i][1]=Y;F+=X0-Xe;}}}void si(){F=0;N=Xe-X0+Y0-Ye; X=X0;Y=Y0;for(i=1;i<=N;i++) {if(F>=0){X++;a[i][0]=X;a[i][1]=Y;F-=Y0-Ye;}else{ Y--;a[i][0]=X;a[i][1]=Y;F+=Xe-X0;}}}void te(){N=Ye-Y0; for(i=1;i<=N;i++) {if(Ye>0){Y++;a[i][0]=X;a[i][1]=Y;}else if(Ye<0){Y--;a[i][0]=X;a[i][1]=Y;}}}void shuchu(){for(i=0;i<=N;i++){printf("%d ",i);printf("%d,%d\n",a[i][0],a[i][1]);}}3．程序结果例如起点（0,0）终点（6,4）步数坐标1 1,02 1,13 2,14 2,25 3,26 4,27 4,38 5,39 6,310 6,4二.圆弧插补1.圆弧插补程序流程图2.圆弧插补程序#include ""#include ""int X0,Y0,X1,Y1,X2,Y2,X3,Y3,X4,Y4; int i=1,r,f,s;void main(){int m;int menu();void yishun();void yini();void ershun();void erni();void sanshun();void sanni();void sishun();void sini();void shuchu();m=menu();switch(m){case 1:yishun();break;case 2:yini();break;case 3:ershun();break;case 4:yini();break;case 5:sanshun();break;case 6:yini();break;case 7:sishun();break;case 8:yini();break;default:printf("无法插补\n"); }}int menu(){int t;printf("输入原点坐标\n");scanf("%d,%d",&X0,&Y0);printf("输入起点坐标\n");scanf("%d,%d",&X3,&Y3);printf("输入终点坐标\n");scanf("%d,%d",&X4,&Y4);printf("1:顺时针圆弧\n");printf("2:逆时针圆弧\n");scanf("%d",&s);X1=X3-X0;Y1=Y3-Y0;X2=X4-X0;Y2=Y4-Y0;r=X1*X1+Y1*Y1;if (X1>=0&&Y1>0&&s==1)t=1;else if (X1>0&&Y1>=0&&s==2) t=2;else if (X1<0&&Y1>=0&&s==1) t=3;else if (X1<=0&&Y1<0&&s==2) t=4;else if (X1<=0&&Y1<0&&s==1) t=5;else if (X1<0&&Y1<=0&&s==2) t=6;else if (X1>0&&Y1<=0&&s==1)t=7;else if (X1>=0&&Y1<0&&s==2)t=8;elset=9;return(t);}void yishun(){do{f=X1*X1+Y1*Y1-r;if(f>=0){Y1--;f-=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{X1++;f+=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(Y1!=0&&(X1!=X2||Y1!=Y2)); if(Y1==0){void sishun();sishun();}}void yini(){do{f=X1*X1+Y1*Y1-r;if(f>=0){X1--;f-=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{Y1++;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(X1!=0&&(X1!=X2||Y1!=Y2)); if(X1==0){void erni();erni();}}void ershun(){do{f=X1*X1+Y1*Y1-r;if(f>=0){X1++;f+=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{Y1++;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(X1!=0&&(X1!=X2||Y1!=Y2)); if(X1==0){void yishun();yishun();}}void erni(){do{f=X1*X1+Y1*Y1-r;if(f>=0){Y1--;f-=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{X1--;f-=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(Y1!=0&&(X1!=X2||Y1!=Y2)); if(Y1==0){void sanni();sanni();}}void sanshun(){do{f=X1*X1+Y1*Y1-r;if(f>=0){Y1++;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{X1--;f-=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(Y1!=0&&(X1!=X2||Y1!=Y2)); if(Y1==0){void ershun();ershun();}}void sanni(){do{f=X1*X1+Y1*Y1-r;if(f>=0){X1++;f+=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{Y1--;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(X1!=0&&(X1!=X2||Y1!=Y2)); if(X1==0){void sini();sini();}}void sishun(){do{f=X1*X1+Y1*Y1-r;if(f>=0){X1--;f-=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{Y1--;f-=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(X1!=0&&(X1!=X2||Y1!=Y2));if(X1==0){void sanshun();sanshun();}}void sini(){do{f=X1*X1+Y1*Y1-r;if(f>=0){Y1++;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{X1++;f+=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(Y1!=0&&(X1!=X2||Y1!=Y2));if(Y1==0){void yini();yini();}}3.程序结果例如圆心（0,0）起点（4,3）终点（4,3）步数坐标0 4,31 3,32 3,43 2,44 2,55 1,56 0,57 0,48 -1,49 -2,410 -3,411 -3,312 -4,313 -4,214 -5,215 -5,116 -5,017 -4,018 -4,-119 -4,-220 -4,-321 -3,322 -3,-423 -2,-424 -2,-525 -1,-526 0,-527 0,-428 1,-429 2,-430 3,-431 3,-332 4,-333 4,-234 5,-235 5,-136 5,037 4,038 4,139 4,240 4,3。