当前位置：文档之家 › 303-电势、电势叠加原理 (1)

303-电势、电势叠加原理 (1)

  • 格式：doc
  • 大小：628.00 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

电工技术：叠加定理解题步骤ppt课件

电工技术：叠加定理解题步骤ppt课件


I 故，各支路电流也增加到原来的3.63倍，即：
1
I2
k
I
' 1
k
I
' 2
4 .7 6 A 7 .6 2 A
I3
k
I
' 3
3 .9 9 A
I4
k
I
' 4
3 .6 3
A
编辑版pppt
9
二、齐次定理
若给定电压变为80V，这相当于电压增
加到原来的2.42倍 (k 80 2.42) 33.02
故，各支路电流也增加到原来的2.42倍，即 ：
递推法
编辑版pppt
8
二、齐次定理
• 递推法 设I4' 1A
若给定电压为120V，这相 当于电压增加到原来的
UB' D22V I3' 1.1A
3.63倍 (k 120 3.63) 33.02
I2' 2.1A
I k I ' 1 2 .3 8 A
UA' D26.2V
I1' 1.31A I ' 3.41A U ' 33.02V
二齐次定理若给定电压为120v这相当于电压增加到原来的363倍1203633302bd22若给定电压变为80v这相当于电压增加到原来的242倍故各支路电流也增加到原来的242倍即二齐次定理802423302感谢亲观看此幻灯片此课件部分内容来源于网络如有侵权请及时联系我们删除谢谢配合
叠加定理（2）
叠加定理解题步骤；齐次定理
编辑版pppt
1
一、叠加定理的应用
叠加定理
（三步走： 1分，2解，3求和 ）
应用 例1：如图电路，求U 。 解： (1)画出分电路图
归纳电工基础ppt课件叠加定理

归纳电工基础ppt课件叠加定理


回顾
怎样用支路电流法的分析复杂直流 电路？
有没有更容易理解，计算更简单 思考 的分析直流电路的方法呢？
..........
2
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ，并增 补指标 。
..........
I″ I″1 R1
I 2″ R2
Is
I 3″ R3
－＋ U″
R4 I ″4
(c)
7
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ，并增 补指标 。
假设E2单独作用时：
..........
5
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ，并增 补指标 。
讲授新课
叠加定理的内容图示
E1和E2同时作用时
例题分析
(2) 当电流源单独作用时, 电压源短路, 如图（c）
所示, 则各支路电流为
I
" 1
R3 R1 R3
Is
3 1 0.6 A 23
I
" 2
R4 R2 R4
Is
0.5 1 1 0.5
0.333 A
I"
I
" 1
I
" 2
(0.6
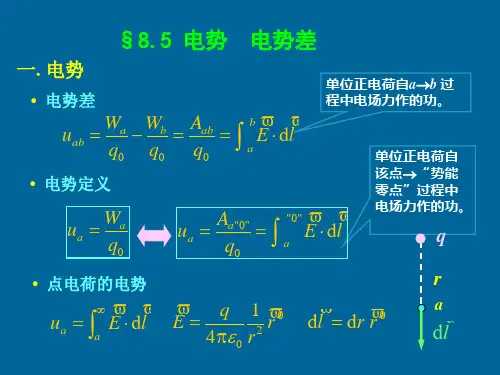
电势电势差

电势电势差


w
W V
1 2
0
E
2
（适用于所有电场）
不均匀电场中 dW wdV
W
dW
V
V
1
2
0
E
2dV
例 已知均匀带电的球体，半径为R，带电量为Q
求 从球心到无穷远处的电场能量
解
E1
Qr
4 0 R3
E2
Q
4 0r 2
Q
R r
取体积元 dV 4r2dr
W1
R
0
1
2
0
E12dV
Q2
40 0R
W2
R12 0 E2 2dV
a
-Q
R2 R1
R2
h R1
l
u R2 Q dr Q ln R2
R1 20lr
20l R1
C Q 20l
u ln(R2 R1)
讨论
R2
h R1
l
若R1>>R2-R1 ,则 C = ?
ln( R2 R1 1) R2 R1
R1
R1
C 0S
d
u
C Q 20l
u ln(R2 R1)
• 电容器的应用：
解
D dS
S
q0i,内
0
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
i
DS 0S D 0
' - - - - - - - - -
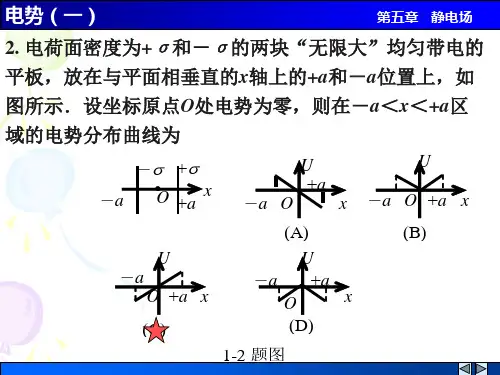
电势一解答

电势一解答


(B) E＝0，U＝
Q
4 0
1 R1
R12．
(C) E＝
Q
4 0r2 ，U＝
Q
4 0 r
Q
R1 r
P
O R2
(D) E＝
Q
4 0r 2 ， U＝
Q
4 0 R1
1-3 题图
电势（一）
解： 由高斯定理可得场强分布为：
E 0(0 r R1)
Q
E 4 0r 2 (R1 r R2 )
U p (r)
P
又因电场线从高电势→低电势，
O
所以UP<UO
2－1题图
电势（一）
第五章 静电场
2. 电荷分别为q1，q2，q3的三个点电荷分别位于同一圆周 的三个点上，如图所示．设无穷远处为电势零点，圆半径
为R，则b点处的电势U＝ 1 8 0 R
2q1 q2 2q3
由电势的叠加原理可得：
U Uq1 Uq2 Uq3
电势（一）
第五章 静电场
5．有N个电量均为q的点电荷，以两种方式分布在相同半
径的圆周上：一种是无规则地分布，另一种是均匀分布．
比较这两种情况下在过圆心O并垂直于圆平面的Z轴上任
z
一点p的场强与电势，则有p（A）场强Fra bibliotek等，电势相等．
（B）场强不等，电势不等．
（C）场强分量Ez相等，电势相等． （D）场强分量Ez相等，电势不等．
定远处Q外1、力Q所3的作情的况功下_，__将8__QQ_22_0从d__Q__1、__Q3连F1线3 中点d 移至Q无2 穷
由题意Q.1所受的合力为零
Q1 F12 o
Q3
Q1
Q2
4 0d 2
第六章(第三讲)电势

第六章(第三讲)电势

§6.4
静电场的环路定理和电势
一、静电场的环路定理 二、电势与电势差 三、电势叠加原理 四、电势的计算
1
§6.4 静电场的环路定理和电势 一 电场力作功的特点 B 1. 点电荷的电场
dA q0 E dl
qq0 r dl 3 rB 4 π 0 r r dl rdl cos rdr qq0 dA dr 2 rA 4 π 0 r q qq0 rB dr A A rA r 2 4 π 0 qq0 1 1 ( ) q 0 E dl 0 L 4 π 0 rA rB
大小
dU E dl n
方向
相反，由高电势处指向低电势处. 与 e n
23
§6.5、等势面 电势的梯度 物理意义 （1）空间某点电场强度的大小取决于该点领 域内电势 U 的空间变化率.
（2）电场强度的方向恒指向电势降落的方向. 直角坐标系中
讨 论
U U U E （ i j k ) gradU x y z
§6.5、等势面 二
电势的梯度
电场线和等势面的关系
1）电场线与等势面处处正交. （等势面上移动电荷，电场力不做功.）
2）等势面密处电场强度大;等势面疏处电梯度 三 电场强度与电势梯度
将单位正电荷由A经 l 移动到B
U U
B
U AB U B U A） E l （ El cos E cos El
q
dl dr E
q
q U 4 π 0 r
q 0,U 0
7
q 0, U 0
r
§6.4
静电场的环路定理和电势
点电荷系 E E i
U A E dl E i dl
电势、电压

电势、电压


四）点电荷系、带电体电场的电势、电势叠加 原理。 + 设一点电荷系：q1、q2----qn qn a 产生电场 E E1 E2 En q1 + q2 + U a E dl ( E1 E2 En ) dl a a q3 +
dr

r
x
2rdr rdr 2 2 2 2 40 r x 2 0 r x
Y
+ + + + +o + + R ++ + ++ Z
dr
p
r
Up
X
R
rdr
2 0 r x
2 2
0
2 2 Up ( R x x) 2 0
2 2 x ( R x x) 2 0
ds
Y
dq
2 2 2 U2 ( R x x) r r xp 2 0
p R 讨论： X 1）x 0 U p x 2 0 2）x R
1 2
dr
2 2 Up ( R x x) 2 0 2
2
1 1 2 (1 Z ) 1 Z Z 2 24
+ d + + + + o+ + R + + + Z ++
ds
Y
dq
p
另解： 分割成点电荷 X
r
x dr
dq
ds rddr dq rddr

R
dU
rddr
电场叠加原理.ppt

电场叠加原理.ppt



p r3
方向如图。

40
(r
ql 2
l2 4
)3
2
思考： 任意点的场 强如何求？

p 40r
3
方向如图。

例7、无限大均匀带电平面中间有一圆孔，求轴上 E =？

R
E
x

两种方法

圆环 R
相减法

例8、均匀带电球面，求轴上 E =？

dl


d R

r
E


dq
dE

dq 40 R 2

Rd 40 R 2
d
R
dE y
y
dEx

dE
Ex


dE x

dE cos
0
2
40
R
cos
d
x
40
E
R
E y
dEy
2
dE sin

sind

0 4 0 R
4 0 R
2、电场有能的性质： 电场力可以移动电场中的带电体。 （电场力对带电体做功）
3、电场
对导体产生静电感应现象。 对绝缘体（介质） 产生极化现象。
二定1、、义电电：场E场强强度度FE
q0
：
电场
(N c
“力的性质”
, V m)
用E
Q

大小:等于单位正电荷受到的力。
描述。
q0
E
F
方向:沿正电荷受力方向。
方向相反。
四 电场强度叠加原理 试验电荷 q0 在点电荷系q1、
大学物理第三章电势

大学物理第三章电势

电势零点
8
P
电荷分布在有限空间， 取无穷远为 U= 0 点。
电位零点的选取： 电荷分布在无限空间， 取有限远点为U= 0 点。 一般工程上， 选大地或设备外壳为U=0点。
9
解题技巧：当场源带电体是球状带电体和柱状带 电体时，无论电势零点取在什么位置， 积分路径都应沿径向向外。此时，
dl dr
19
本题令 U r l 0 电场中任一点的电势 U P P 柱体内 ( r R)
U P1
电势零点 P 1
电势零点
E cosdr
U P E cosdr
电势零点
P
E cosdr E1dr E2 dr R
R r
l
柱外筒内 ( R r R1 )
7
五、电势 (Electric Potential) *场中任一点P的电势
U P E cos dl
P c
当取电场中某一点c为电势零点（即:令Uc = 0）时，

电势零点
P
E cos dl
即：电场中任意一点P的电势等于电场强度从P点 经任一路径到电势零点的积分。
U P E cos dl
qo

5
二、 静电场的保守性（静电场环路定理）

L
E dl 0
a
L2
.
qo
L1
b
.
在静电场中，场强沿任意闭合路径的线积 分等于零。即：对任何静电场，电场强度的 线积分都只取决于起点和终点的位置，而与连 接起点和终点间的路径无关。
6
三、电势能差
Aab Wa Wb qo a 实验电荷qo 在静电场中从a运动到b时，静电场力
电路原理：叠加定理ppt课件

电路原理：叠加定理ppt课件

.
is1单独作用
1
1
+
G1
i2 (2) G2 i3 (2)
+
G3 +
G1
பைடு நூலகம்
i2 (3) G2 i3 (3)
G3
+
us2
us3
–
–
us2单独作用
us3单独作用
待求元件的功率计算不能使用叠加定理 (功率不 是电压或电流的一次函数)。
叠加结果是代数和，要注意电压或电流的参考方向。
.
4. 叠加定理的主要用途
4.1 叠加定理 学习目标
1、理解并准确掌握该定理的内容。 2、明确该定理的适用范围及要点。 3、明确该定理的用途。 4、熟练掌握该定理使用方法。
.
1. 叠加定理的内容
在线性电路中，任一支路的电压或电流等于该电 路中各个独立电源单独作用时在该支路所产生的电压 或电流的代数和。
1
u+1 R1
–
u+s
i2
i3
R2
iS
–
.
2. 叠加定理适用范围及要点说明
叠加定理只适用于线性电路， 不适用于非线性电路。
一个独立电源单独作用，其余 独立电源置零。
电压源置零—短路 电流源置零—开路
1
G1
i2
G2
i3
is1
+
us2
–
G3
= + us3
–
1
G1
i2 (1) G2 i3 (1)
G3
is1
三个电源共同作用
主要用于线性电路分析，有时可以简化计算。
5. 叠加定理的意义
叠加定理反映出线性电路中各独立电源的独立性。
电势讲解

电势讲解


Aab q E dl q( a b )
a
b
二. 电势的计算
1. 点电荷场电势公式
P E dl
P

Q
O

r
P

E dl

r
E dl
r
r

Q 40 r
2 r
e dr
r
Q 4 0 r
Q 4 0 r
2
dr
dl dr
a
b
a、b两点电势差
预选一个参考位置为电势零点
若选 b 点为电势零点( 令 b 0 )则，a 点的 b 电势：
b
a b E dl a
a
零点
b
零点
a
E dl
E
a a
q

a
E d l
讨论
(1) 电势零点的选择(参考点)
E 2 0
选 0，则电场内任一点 P 的电势为
E dl E dl Ε
p p


故，对于这样的电场只能选取空间有限远 处某一定点为电势零点。
一般选在无限长带电直线上、无限长圆柱的面上 或轴线上、无限大带电平面的面上。
(2) 电势的量纲
SI制：单位 V (伏特) (3) 若电势分布已知，一点电荷 q 从 a 点运 动到 b 点，静电力做功
dr
dq 2rdr
r
o
R
x2 r 2
x
d P
P
dq
2
x
2
40 x r
P
1 4 0
电势1

电势1


∴ Aab = q0 ∫ E ⋅ dl = q0ϕ ab
a
bபைடு நூலகம்
Aab = q0ϕab ——电场力的功与电势差的关系 电场力的功与电势差的关系
§11.7 电势的计算 方法一： 方法一：利用电势的定义
注：利用 ϕ a = ∫ E ⋅ dl (ϕ c = 0 ) 求电势时 (1)要求电场分布已知或不难求出； 要求电场分布已知或不难求出； 要求电场分布已知或不难求出 (2)明确电势零点； 明确电势零点； 明确电势零点 (3)积分与路径无关 选最佳路径。 积分与路径无关→选最佳路径 积分与路径无关 选最佳路径。 (4)当积分路径上 E的表达式不同时要分段积分。 当积分路径上 的表达式不同时要分段积分。 例1. 求均匀带电球面的电场中的电势分布。 设球 求均匀带电球面的电场中的电势分布。 面半径为R，总带电量为q. 面半径为 ，总带电量为 解： 对均匀带电球面： 对均匀带电球面：
a c c
W a = q 0 ∫ E ⋅ dl
a
(Wc = 0 )
某点(a)的电势能等于将 参考点c电力所作 某点 的电势能等于将q0由a →参考点 电力所作 的电势能等于将 参考点 的功，它为q0 和产生电场的源电荷系统所共有。 的功，它为 和产生电场的源电荷系统所共有。
▲参考点的选择有任意性。一般情况下： 参考点的选择有任意性 一般情况下： 有限大小的带电体的场，通常选无穷远处为 的带电体的场 无穷远处 对有限大小的带电体的场，通常选无穷远处为 参考点： 参考点：W∞ = 0. 对无限大带电体的场， 对无限大带电体的场，一定不选无穷远处为 参考点，而选有限远处某点为参考点。 参考点，而选有限远处某点为参考点。 电工中：常选大地或机壳、公共线为参考点。 电工中：常选大地或机壳、公共线为参考点。 或机壳 为参考点 2、电势(electric potential) 、电势

第十四章 电势


P E1
R
q
E2
U2

E 2d r

q q dr 2 4 o r 4 o r
静电平衡导体内部和导体表面电势处处相等，整个导 体是个等势体。
例：半径为R的均匀带电球体，带电量为q。 求电势分布。 解：
1 SE d S o q i
3 2
q
1 q 4 r E 1 4 r 3 o 4 R 3 3
一周电场力做的功。 环流定理的物理意义
静电场是一个保守力场,有势场(无旋场)
§14.2 电势差和电势
静电场是保守场 仅与位置有关的函数，电势能
b
(W b W a ) q 0 E d l A
a
W 而 称为电场在该场点的电势,用U来表示 q0
Wb Wa ( ) E dl q0 q0 a
2 2
U2


r
E 2dr


r
q q dr 2 4 o r 4 o r
习题：如图所示，两个同心的均匀带电球面， 内球面半径为R1、带电荷Q1，外球面半径为 R2、带有电荷Q2．设无穷远处为电势零点， 则在内球面之内、距离球心为r处的P点的电 势U为： Q2 (A) Q1 Q2
对连续分布电荷:
dq U 4 0 r
体电荷密度 电荷密度 面电荷密度 线电荷密度
dq dV dq dS
dq dl
习题：在点电荷+q的电场中，若取图中P点处为电势 零点 ， 则M点的电势为
+q P M
q (A) 4 0 a
a
a
(B) (C)
q 8 0 a
UM

势的叠加原理应用

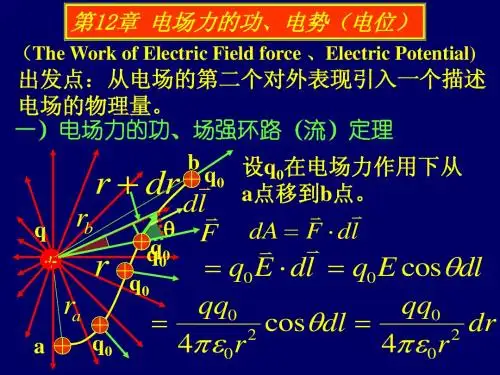
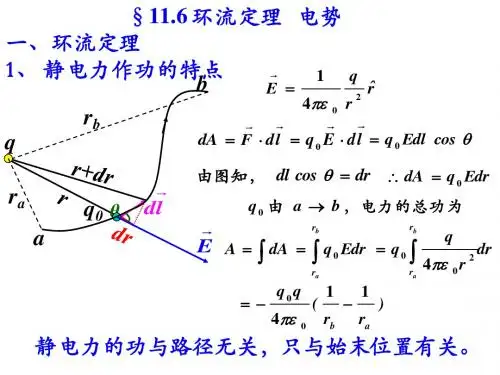
势的叠加原理应用什么是势的叠加原理势的叠加原理是指当多个势函数作用于同一系统时，系统的总势函数可以看作是各个势函数的叠加。

其基本原理是势函数是标量，满足可加性。

这一原理在物理学中有广泛的应用，特别是在电磁学中，可以通过叠加不同电荷的势函数来计算电场。

在应用势的叠加原理时，需要注意势函数之间的线性性和可加性。

此外，还需要确定合适的边界条件和适当的坐标系，以便计算和分析系统的总势函数。

势的叠加原理在电磁学中的应用势的叠加原理在电磁学中有广泛的应用。

我们知道，电场和磁场可以用势函数表示，分别为电势和磁矢势。

根据势的叠加原理，当多个电荷或电流作用于同一点时，可以将它们的电势和磁矢势进行叠加，从而得到总的电势和磁矢势。

具体来说，对于电势的叠加，我们可以通过线性叠加不同电荷的电势函数来求解系统的总电势。

假设有多个电荷分别位于不同的位置，那么对于某个位置的电势，可以通过对每个电荷的电势进行求和得到。

对于磁矢势的叠加，同样可以通过线性叠加不同电流的磁矢势函数来求解系统的总磁矢势。

假设有多个电流分别位于不同的位置，那么对于某个位置的磁矢势，可以通过对每个电流的磁矢势进行求和得到。

势的叠加原理在电场计算中的应用举例为了更好地理解势的叠加原理的应用，我们可以通过一个简单的例子来说明。

假设有两个点电荷+Q和-Q，它们分别位于A点和B点。

现在我们要计算这两个点电荷所产生的电场在点C处的电势。

首先，我们可以根据库仑定律计算出点电荷+Q在点C处的电势为：V1 = k * Q / r1其中，k为库仑常数，r1为AC的距离，即A点到C点的距离。

同样地，我们也可以计算出点电荷-Q在点C处的电势为：V2 = -k * Q / r2其中，r2为BC的距离，即B点到C点的距离。

根据势的叠加原理，点C处的总电势应为这两个电荷产生的电势之和：V = V1 + V2将上述公式代入，可得到点C处的总电势表达式。

在这个例子中，我们可以看到通过势的叠加原理，可以将多个点电荷产生的电势相加，从而得到总的电势。

大学物理学第11章电势

38
例1 求电矩为 p=ql 的电偶极子在均匀外电场 E 中的电势能
l A
-q
B +q
θ
E
讨论:
39
§11.7 静电场的能量 电场能量密度
电场总能量
积分遍及整个空间
注意：电场能量存在于场强所在的全部空间
40
例2 在真空中一个均匀带电球体,半径为R,总电量为q,试利用电 场 能量公式求此带电系统的静电能。 思路分析： （1）确定电场分布；
R
（2）确定能量密度； （3）从电场能量定义出发求电场能量；
41
++
+
+
+R + +
+
+
+ +r
+ +
+ +
+ +
o +
+ dr +
+
+
+ + +
+++ +
42
期末复习.doc
解：思路分析：
+++ +
+R
o
+
（1）确定电势零点——无穷远处；
q+ （2）用高斯定律确定电场分布；
+ +
+
+ ++
+
+ + （3）确定电势分布；
10
++ +
+
+R
+
o
+ +++

电路 叠加原理

电路叠加原理电路叠加原理是电路分析中的基本原理之一。

它指出，在只有源一次被激活的情况下，电路中的各元件的电压或电流是可以分别计算的。

这个原理的应用可以帮助我们更加简单、方便地对电路进行分析和设计。

在本篇文章中，我们将探讨电路的叠加原理及其常见应用。

一、电路叠加原理的定义在理解电路叠加原理之前，我们先来看看什么是电路。

电路是由电阻、电容、电感、电源等元件连接而成的，能够实现特定功能的电子系统。

在电路中，每一个元件都有其自身的电流和电压。

而叠加原理指出，在电路中每个元件所受到的电流和电压可以分别计算。

换句话说，我们可以将不同元件产生的电压和电流分别计算，最后汇总成最终结果，这就是电路叠加原理。

二、叠加原理的原理叠加原理的应用基于超额原理。

所谓超额原理是指，在电路分析时，我们可以分别处理每一个源的影响，再将它们分别计算出来，然后把它们加在一起，不考虑其互相影响的结果。

这是因为，每一个电源的作用可以看做只受其本身电量电势的影响，与其他电源或元件的状态无关。

叠加原理的描述可以用克希荷夫定律来简单表示。

根据克希荷夫定律，一条电路中的电流总和等于电源电势和电路中的所有电阻的电压之和。

利用这个原理，我们可以将每个源的电路分离开来，分别求出它们的电流或电压，最终再将它们加在一起，得到整个电路的输入输出特性。

三、叠加原理的应用叠加原理在电路分析中应用非常广泛，下面我们来看看其常见的应用。

1.电压分压器分析应用在分析电路时，常常需要计算不同元件处的电压。

比如，电压分压器中，我们需要计算两端电阻器上的电压。

假设电压分压器中，有两个电源分别加在两个电阻上。

在计算时，我们可以先将一个电源断开，然后将另一个电源中的电压与电阻上的电压相加，以获得该电源产生的总电压。

然后，将这个计算结果与另一个电源的计算结果相加，就可以得到电压分压器的总输出电压了。

2.电阻网络分析应用在分析复杂的电路中，我们常常需要对电阻网络进行分析。

在这种情况下，我们可以使用叠加原理来降低分析复杂度，简化计算。

静电学中的电场的叠加与相对电势


静电除尘器：利用电场叠加原理，使尘埃颗粒带电并吸附在电极上，实现空气净化。
电子显微镜：通过控制电场和相对电势，实现对样品的精确聚焦和成像。
离子推进器：利用电场叠加原理加速离子流，产生强大推力。
电磁感应：利用磁场变化产生电场，实现电能与磁能的相互转换，应用于发电机和变压器等设 备。
汇报人：XX
XX,a click to unlimited possibilities
汇报人：XX
CONTENTS
ห้องสมุดไป่ตู้
PART ONE
PART TWO
电场叠加定义：多个电场在同一空间内相互作用，形成合电场 电场叠加原理公式：E=E1+E2+…+En 电场叠加原理应用：计算复杂电场分布、预测电荷运动轨迹等 电场叠加原理注意事项：考虑电场矢量合成与标量叠加的区别
相对电势是描述电场中电势差的一 种方式，可以用来描述电场中不同 位置的电势差。
当多个电场共同作用时，相对电势的 大小和方向将影响最终的电场分布， 因此相对电势的变化将导致电场分布 的变化。
添加标题
添加标题
添加标题
添加标题
在静电学中，电场叠加是指多个电 场共同作用的结果，相对电势在电 场叠加中起到重要的作用。
相对电势可以用 于计算电场中电 荷的能量
相对电势的引入有 助于理解电场中的 能量转移和转化
相对电势是描述电场中电势差的一 种方式
相对电势差是电场中两点间电势的 差值
添加标题
添加标题
相对电势差与电场强度成正比
添加标题
添加标题
相对电势差与电场力做功有关
静电屏蔽：利 用相对电势的 概念，可以有 效地屏蔽外部 电场对物体的
电场叠加可以用于 计算电场力、电势 能等物理量
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

电势、电势叠加原理1．选择题1．静电场中某点电势在数值上等于()A 试验电荷0q 置于该点时具有的电势能； ()B 单位试验电荷置于该点时具有的电势能；()C 单位正电荷置于该点时具有的电势能；()D 把单位正电荷从该点移到电势零点外力所作的功。

〔 〕2．边长为0.3m 的正三角形 abc ，顶点a 处有一电量为810C -的正点电荷，顶点b 处有一电量为810C-的负电荷，则顶点c 处的场强E 和电势U 的大小分别为92-201910N m C 4πε⎡⎤=⨯⋅⋅⎢⎥⎣⎦：()A 0E =，0U =； ()B 1000(V/m)E =，600V U =； ()C 1000(V/m)E =，0V U =； ()D 2000(V/m)E =，600V U =。

〔 〕3．如图所示，下面表述中正确的是：()A A B C E E E >> A B CU U E >>； ()B A B C E E E << A B C U U E >>； ()C A B C E E E >> A B CU U E <<； ()D A B C E E E << A B CU U E <<。

〔 〕4．边长为a 的正方形，在其四个顶角上各放一个等量的点电荷，若正方形中心处的场强和电势都为零（设无穷远处电势为零），则：()A 在四个顶角上都应放上正电荷。

()B 在四个顶角上都应放上负电荷。

()C 在两个对顶角上应放上正电荷，而另外两个对顶角上应放上负电荷。

()D 在两个相邻的顶角上应放上正电荷，而另外两个相邻的顶角上应放上负电荷。

〔 〕5．真空中有一点电荷Q ，在与它相距为r 的a 点处有一试验电荷q 。

现使试验电荷q 从a 点沿半圆弧轨道运动到b 点，如图所示。

则电场力对q 作功为()A 22042Qq r r επ⋅π； ()B 2024Qq r r πε； ()C 204Qq r r ππε； ()D 0． 〔 〕6．如图所示，a 、b 、c 是电场中某条电场线上的三个点，由此可知：()A a b c E E E >> ； ()B a b c E E E << ；()C a b c U U E >> ； ()D a b c U U E << 。

〔 〕7．如图所示，直线MN 长为2l ，弧OCD 是以N 点为中心，l 为半径的半圆弧，N 点有正电荷q +，M 点有负电荷q -。

今将一试验电荷0q +从O 点出发沿路径OCDP 移到无穷远处，设无穷远处电势为零，则电场力作功()A A <0， 且为有限常量；()B A>0 ，且为有限常量； ()C A=∞； ()D A =0。

〔 〕8．已知某电场的电场线分布情况如图所示．现观察到一负电荷从M 点移到N 点．有人根据这个图作出下列几点结论，其中哪点是正确的？ ()A 电场强度M N E E <； ()B 电势M N U U <；()C 电势能M N W W < ； ()D 电场力的功0A >。

〔 〕9．点电荷Q -位于圆心O 处，a 是一固定点，b 、c 、d 为同一圆周上的三点，如图所示。

现将一试验电荷从a 点分别移动到b 、c 、d 各点，则()A 从a 到b ，电场力作功最大；()B 从a 到到c ，电场力作功最大；()C 从a 到d ，电场力作功最大；()D 从a 到各点，电场力作功相等。

〔 〕10．已知均匀带正电圆盘的静电场的电力线分布如图所示。

由这电力线分布图可断定圆盘边缘处一点P 的电势与中心O 处的电势的大小关系是： ()A P O U U =； ()B P O U U <；()C P O U U >； ()D 无法确定的(因不知场强公式)。

〔 〕11．在静电场中，电场线为均匀分布的平行直线的区域内，在电场线方向上任意两点的电场强度E 和电势U 相比较：()A E 相同，U 不同； ()B E 不同，U 相同； ()C E 不同，U 不同； ()D E 相同，U 相同。

〔 〕12．有四个等量点电荷在OXY 平面上的四种不同组态，所有点电荷均与原点等距。

设无穷远处电势为零，则原点O 处电场强度和电势均为零的组态是 ：〔 〕13．在点电荷q +的电场中，若取图中P 点处为电势零点，则M 点的电势为：()Aaq 04πε； ()Baq 08πε； ()C aq 04πε-； ()D aq 08πε-。

〔 〕2．判断题1．静电场中某点电势值的正负取决于电势零点的选取。

2．静电场中某点电势值的正负取决于产生电场的电荷的正负。

3．在已知静电场分布的条件下，任意两点1P 和2P 之间的电势差决定于1P 和2P 两点的位置。

4．电荷在电势高的地方静电势能一定大。

5．正电荷在电势高的地方，电势能也一定高。

6．电场强度的方向总是指向电势降落的方向。

7．场强和电势都是矢量。

3．填空题1．可以引入电位（势）来描述静电场的原因是 。

2．如图所示，在静电场中，一电荷0q 沿正三角形的一边从a 点移动到b 点，电场力作功为0A ，则当该电荷0q 沿正三角形的另二条边从b 点经c 点到a 点的过程中，电场力做功A = 。

3．两个点电荷的带电量分别为Q 和q ，它们相距为a 。

当q 由2Q 变到4Q时，在它们的连线中点处的电势变为原来的 倍。

（以无限远处的电势为零）4．一半径为R 的均匀带电球面，带有电荷Q 。

若规定该球面上的电势值为零，则无限远处的电势将等于 。

5．图中所示以O 为圆心的各圆弧为静电场的等势线图， 已知123U U U << ，则a 、b 两点电场强度的大小：a E ________b E （填 ＞、＝、＜）。

6．如图所示，在电荷为q 的点电荷的静电场中，将一电荷为0q 的试验电荷从a 点经任意路径移动到b 点，外力所作的功A ＝___ _______。

a bc7．如图所示，两个点电荷q +和3q -，相距为d ，若选无穷远处电势为零。

则两点电荷之间电势0U =的点与电荷为q +的点电荷相距多远？ 。

8．一个半径为R 的均匀带电球面，带电量为Q 。

若规定该球面上电势为零，则球面外距球心r 处的P 点的电势P U =______________________。

9．一电量为Q 的点电荷固定在空间某点上，将另一电量为q 的点电荷放在与Q 相距r 处。

若设两点电荷相距无限远时电势能为零，则此时的电势能e W =_________________。

10．如图所示，半径为R 的均匀带电球面，总电荷为Q ，设无穷远处的电势为零，则球内距离球心为r 的P 点处的电势为_________________。

11．电量为q 的三个点电荷分别位于同一个圆周的三个点上，如图所示。

设无穷远处为电势零点，圆半径为R ，则b 点处的电势U 是______________。

4．计算题1．（1）（本小题5分）一根长为L 的细棒，弯成半圆形，其上均匀带电，电荷线密度为λ+，试求在圆心O 点的电势。

（2）（本小题5分）如图所示，在A ，B 两点处放有电量分别为q +,q -的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求:移动过程中电场力作的功(无穷远为电势零点)。

2．（1）（本小题5分）两个带等量异号电荷的均匀带电同心球面，半径分别为10.03m R =和20.10m R =。

已知两者的电势差为450V ，求：内球面上所带的电荷。

［92201910N m /C 4πε=⨯⋅］（2）（本小题5分）电荷q 均匀分布在长为2l 的细杆上。

求：在杆外延长线上与杆端距离为a 的P 点的电势（设无穷远处为电势零点）。

3．电荷以相同的面密度σ分布在半径为110cm r =和220cm r =的两个同心球面上。

设无限远处电势为零，球心处的电势为0300V U =。

［92201910N m /C 4πε=⨯⋅］(1) 求电荷面密度σ；(2) 若要使球心处的电势也为零，外球面上应放掉多少电荷？4．如图所示，在电偶极矩为e p的电偶极子的电场中，将一电荷为q 的点电荷从A 点沿半径为R 的圆弧（圆心与电偶极子中心重合，R >>电偶极子正负电荷之间距离）移到B 点，（1）以圆弧的圆心为座标原点，求电偶极子的电势分布；（2）在此过程中电场力所作的功(设无穷远处为电势零点)。

5．如图所示，有三个点电荷1Q ，2Q ，3Q 沿一条直线等间距分布，已知其中任一点电荷所受合力均为零，且13Q Q Q ==。

求在固定1Q ，3Q 的情况下，将2Q 从O 点推到无穷远处外力所作的功。

6．如图所示，AO=OB=R ，OCD 为以B 为中心的半圆弧，A 、B 两点分别放置电荷+q 和-q ，求：(1) O 点与D 点的电势 O U 与 D U （设无穷远处电势为零）；(2) 把正电荷0q 从O 点沿弧OCD 移到D 点，电场力做的功；(3) 把单位正电荷从D 点沿AB 延长线移到无穷远处电场力做的功。