电势叠加原理 文档

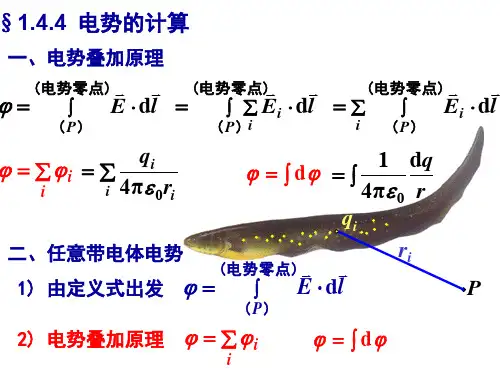
电场的叠加和电势的计算在物理学中，电场是指某个空间内由电荷引起的力场。

当存在多个电荷时，它们的电场可以相互叠加，产生一个合成的电场。

而电势则是描述电荷在电场中的能量状态，计算电势可以帮助我们理解电荷的分布和电场的特性。

一、电场的叠加当存在多个电荷时，它们所产生的电场可以相互叠加。

根据库仑定律，电荷之间的相互作用力与它们之间的距离成反比，与电荷量的乘积成正比。

因此，对于一个点电荷Q1和另一个点电荷Q2之间的作用力可以表示为：F12 = k * (Q1 * Q2) / r12^2其中，F12表示1号电荷作用在2号电荷上的力，Q1和Q2分别为两个电荷的电荷量，r12为它们之间的距离，k为库仑常数。

根据叠加原理，当多个电荷同时存在时，它们所产生的电场可以简单地叠加在一起。

假设有两个电荷Q1和Q2，在某一点P处受到的合成电场E为：E = E1 + E2其中，E1为点电荷Q1在点P处产生的电场强度，E2为点电荷Q2在点P处产生的电场强度。

根据库仑定律，电场强度与电荷量的比值成正比，与距离的平方成反比。

同理，对于更多的电荷，其电场强度的叠加可以通过求和的方式得到：E = E1 + E2 + ... + En其中，En为第n个电荷在点P处产生的电场强度。

二、电势的计算在电场中，电势是描述电荷所具有的能量状态的物理量。

电势可以通过电荷在电场中的位移来计算。

在电场中，单位正电荷从无穷远处移到某一点的过程中，所需做的功数值被定义为该点的电势。

对于一个电荷Q在某一点P处产生的电势V，可以计算为：V = k * (Q / r)其中，Q为电荷量，r为电荷到点P的距离，k为库仑常数。

同样地，对于多个电荷，它们在某一点P处产生的电势的叠加也可以通过求和的方式得到：V = V1 + V2 + ... + Vn其中，Vn为第n个电荷在点P处产生的电势。

需要注意的是，电场和电势是互相关联的物理量。

电场是描述电荷产生的力场，而电势则是描述电荷在电场中的能量状态。

第六讲电势
内容：§9－6
1．电势和电势差
2．电势叠加原理
3．电势的计算
要求：
1．掌握电势叠加原理；
2．掌握电势的两种计算方法。

重点与难点：
3．电势的计算方法。

作业：
习题：P39：21，22
意大利物理学家。

伏打在物理学方面做出了许多重要贡献，他发明过起电盘，发明过验电器、储电器等多种静电实验仪器。

伏打最显赫的功绩是发明了伏打电池。

伏打电池的出现对电学的发展却产生的深远的影响，开创了一个新的广阔天地，成为人类征服自然的最有力的武
伽伐尼在1786年和1792年在实验中观察到用铜钩挂起来的蛙腿在碰到铁架时会发生痉挛。

他认为这是生物电产生的效果。

伏打认为上述现象的产生是由于两种不同金属接触时所产生的电效应。

两种观点曾引起了十年之久的争论。

3．电势差
在静电场中，任意两点-=V U。

静电场中电势叠加看过来1 问题提出 近几年高考物理试题中频繁出现点电荷周围电势叠加的题型，学生感到很困惑．场强叠加比较常见，教材中也有明确要求．与场强不同的是，电势的叠加在教材中不明确，教师重视程度不够，对试题边界模糊不清．电势的叠加是空间某点的电势等于各点电荷或各部分电荷单独存在该点的电势的代数和，而不是矢量和．两个点电荷周围电势的叠加一般用点电荷周围的等势线（或面）或电势φ随x 变化的关系进行判断，在涉及三个或三个以上点电荷周围电势叠加问题时，前面两种方法就不适用了．虽中学阶段不涉及点电荷周围电势的定量计算，但是它确实是有公式的，对于真空中电量为Q 的静止点电荷而言，当选取离点电荷无穷远处的电势为零时，离点电荷距离为r 处电势为rkQ =ϕ（k 为静电力常量）．通过公式分析，我们得出结论：取无穷远处电势为零，正电荷周围电势为正，且离正电荷越近电势越高，离正电荷越远电势越低；负电荷周围电势为负，且离负电荷越近电势越低，负电荷越远电势越高．在涉及多个点电荷周围电势的叠加问题时，我们就用这个结论来定性或半定量分析，比较方便，下面举例说明，以飨读者．2 结论应用【例1】 (多选)如图1所示，处于x 轴上的两个等量异号点电荷＋Q 和－Q ，坐标分别为(L,0)和(3L,0)．以坐标原点O 为圆心，作半径为2L 的圆，圆上有a 、b 、c 、d 四个点，均处于两点电荷形成的电场中．则下列说法正确的是( )A ．O 点电势等于b 点电势B ．b 点和d 点电场强度大小相等，电势相同C ．将一正试探电荷从c 点沿虚线圆周移到O 点电场力不做功D ．将一正试探电荷从b 点沿y 轴移到d 点，电势能先增大后减小【答案】 BD 【解析】 由等量异号点电荷的电场线、等势线分布图，如图2所示，可知φO >φb ，故A 错误；如图2根据对称性，b 、d 两点场强大小相等、电势相同，故B 正确；取无穷远处电势为零，c 点电势也为零，由图2知，沿电场线方向电势逐渐降低，O 点电势大于零，所以将正试探电荷从c 点沿虚线圆周移到O 点电场力做负功，故C 错误；由图2知φb ＝φd ＜φO ，所以将正试探电荷从b 点沿y 轴经O 点移到d 点，电势能先增大后减小，故D 正确．【点评】对等量异（同）号点电荷周围的电势叠加，我们可直接根据电场线、等势线分布图求解，也可根据结论求解，题中O 点距离＋Q 比－Q 近，显然O 点电势为正，虽然b 点距离＋Q 也比－Q 近，但O 点与b 点相比离得更近．显然离得越近的影响越大，所以φO >φb ，作为选择题，很明显O 、b 两点电势不等，A 错误．在实际做题中，我们可以将几种方法结合起来，这样更简便．【例2】两点电荷量分别为q 1和q 2的点电荷放在x 轴上的O 、M 两点，两电荷连线上各点电势φ随x 变化的关系如图3所示，其中A 、N 两点的电势均为零，ND 段中的C 点电势最高，则（ ） 图1图2A ．A 、N 两点电场强度的大小相等B ．将一个正点电荷放在x 轴负半轴时，它将会一直向x 轴负方向做加速运动C ．NC 间场强方向向x 轴正方向D ．将一正点电荷从N 点移到D 点，电场力先做负功后做正功【答案】 BD 【解析】 A 、N 两点电场强度的大小为该点在电势随x 变化的关系曲线的斜率大小，在A 、N 两点的斜率大小明显不为零，故A 项错误．沿着电场线的方向电势降低，根据q 1和q 2之间电势的变化曲线可以得到，q 1带正电荷、q 2带负电荷，根据零电势点的位置（近小远大）可知，q 1所带电荷量的大小大于q 2所带电荷量的大小，然后根据异种电荷所形成的电场规律可知，将一个正点电荷放在x 轴负半轴时，它将会一直向x 轴负方向做加速运动，故B 项正确．电势沿着电场线方向减小，可得NC 间场强方向向x 轴负方向，故C 项错误．根据φ-x 曲线可知，从N 点到D 点电势为正值且先增加后减小，且带电粒子带正电，根据ϕq E W P ∆-=∆-=可知，电场力先做负功后做正功，故D 项正确．【点评】题目已知电势φ随x 变化的函数图像，对电势高低的判断直接由图像读取．进一步可以利用φ-x 图象的斜率判断沿x 方向电场强度E x 随位置变化的规律．斜率的大小表示电场强度的大小，斜率的正负表示电场强度的方向，进而判断电荷的受力．还可根据电势大小关系分析电荷移动时电势能的变化和电场力做功情况．近小远大也体现了点电荷周围电势的大小关系．【例3】 (2015年江苏卷)两个相同的负点电荷和一个正点电荷附近的电场线分布如图4所示．c 是两负电荷连线的中点，d 点在正电荷的正上方，c 、d 到正电荷的距离相等，则( )A ．a 点的电场强度比b 点的大B ．a 点的电势比b 点的高C ．c 点的电场强度比d 点的大D ．c 点的电势比d 点的低 【答案】 ACD 【解析】 由题4图知，a 点处的电场线比b 点处的电场线密集，所以E a ＞E b ，A 项正确；由沿电场线方向电势逐渐降低可知φb ＞φa ，B 项错误；由场强公式E ＝k Q r 2和场强叠加原理可知E c ＞E d ，C 项正确；取无穷远处电势为零，正电荷周围电势为正，且离正电荷越近电势越高；负电荷周围电势为负，且离负电荷越近电势越低．c 、d 距离正电荷相同，c 比d 距离负电荷近，这里不管正电荷的影响，主要看研究的位置离负电荷的远近来分析电势，所以φd ＞φc ，D 项正确．【点评】 本题非常有新意，把考生熟悉的两个点电荷拓展到了三个点电荷，属于进阶式考题，对于三个点电荷的电势叠加情形，教材里没有固有的电场线和等势线分布图可参考，对考生来说是个难点，还好一般这样的考试题都以定性为主，我们用结论来分析，c 、d 两点的电势就迎刃而解了．【例4】如图5所示，现有两个边长不等的正方形ABCD 和abcd ，且Aa 、Bb 、Cc 、Dd 间距相等．在AB 、AC 、CD 、DB 的中点分别放等量的点电荷，其中AB 、AC 的中点放的点电荷带正电，CD 、BD 的中点放的点电荷带负电，取无穷远处电势为零．则下列说法中正确的是（ ）图3 图4A ．O 点的电场强度和电势均为零B ．把一负点电荷沿着b →d →c 的路径移动时，电场力所做总功为零C ．同一点电荷在a 、d 两点所受电场力不同D ．将一负点电荷由a 点移到b 点电势能减小【答案】B 【解析】上下两个正负点电荷在O 点将产生的电场强度向下，左右两个电荷正负点电荷在O 点的电场强度向右，根据矢量合成法则可以知道O 点电场强度不为零，方向沿为AD 方向，O 离四个点电荷距离相同，四个点电荷在O 点处电势为零，故A 错误．据对称性，b 、c 等电势，把一负点电荷沿着b→d→c 的路径移动时，电场力做功为零，所以B 选项正确．按照库仑定律和力的合成，同一点电荷在a 、d 两点所受电场力相同，故C 错误．取无穷远处电势为零，由结论知，在a 点的电势为正，b 、O 、c 三点电势相等均为零，则负点电荷由a 点移到b 点电势能增加，故D 错误．【点评】对于多个（三个以上）点电荷的电势叠加情形，我们以此类推，仍然依据“取无穷远处电势为零，正电荷周围电势为正，且离正电荷越近电势越高，离正电荷越远电势越低；负电荷周围电势为负，且离负电荷越近电势越低，负电荷越远电势越高．”定性分析，再结合场强、电场力、电势能、电势差等知识分析得出正确结论，一般来说，高考命题涉及静电场的题目以选择题为主，且四个选项会涉及从力的、能的角度来描述电场的较多物理量的考察，场强、电势的叠加只是其中一部分，综合理解、运用场强、电场力、电场线、电势、电势能、电势差、等势面等概念及其关系是解题的关键．在研究高考试题过程中我们发现，电势属于Ⅰ级要求，教材上也未涉及电势的叠加，有的人认为超纲了，但在大学物理教材中是必须掌握的知识，同时它也能很好地考察学生的核心素养（物理观念、科学思维）和关键能力，高考的核心功能是“立德树人、服务选才、引导教学”，既然是选拔人才，定性地分析电场叠加那就自然不超纲，既然在2015年的江苏卷中出现了，接下来必将是高考物理试题中的常客． 3 小试牛刀1.（2022河北卷）如图，真空中电荷量为2q 和(0)q q ->的两个点电荷分别位于M 点与N 点，形成一个以MN 延长线上O 点为球心，电势为零的等势面（取无穷处电势为零），P 为MN 连线上的一点，S 为等势面与直线MN 的交点，T 为等势面上的一点，下列说法正确的是（ ）A. P 点电势低于S 点电势B. T 点电场强度方向指向O 点C. 除无穷远处外，MN 直线上还存在两个电场强度为零的点D. 将正试探电荷0q 从T 点移到P 点，静电力做正功【答案】B 【解析】A ．在直线MN 上，左边正电荷在M 右侧电场强度水平向右，右边负电荷在直线MN 上电场强度水平向右，根据电场的叠加可知MN 间的电场强度水平向右，沿着电场线电势逐渐降低，可知P 点电势高于等势面与MN 交点处电势，则P 点电势高于S 点电势，故A 错误；C ．由于正电荷的电荷量大于负电荷电荷量，可知在N 左侧电场强度不可能为零，则N 右侧，设MN 距离为L ，根据222()()k q k q L d d ⋅⋅=+图5可知除无穷远处外，直线MN 电场强度为零的点只有一个，故C 错误；D ．由A 选项分析可知：T 点电势低于P 电势，则正电荷在T 点的电势能低于在P 电势的电势能，将正试探电荷0q 从T 点移到P 点，电势能增大，静电力做负功，故D 错误；B ．设等势圆的半径为R ，AN 距离为x ，MN 距离为L ，如图所示，根据kq x ϕ=，结合电势的叠加原理A 、S 满足2k q kq L x x ⋅=-，222k q kq L R x R x ⋅=+--，解得3L x =，23L R =由于电场强度方向垂直等势面，可知T 点的场强方向必过等势面的圆心，O 点电势23233O k q kq kq L L L L ϕ⋅=-=-+，可知T O ϕϕ>可知T 点电场方向指向O 点，故B 正确．故选B ．2.（2021河北卷）如图，四个电荷量均为()0q q >的点电荷分别放置于菱形的四个顶点，其坐标分别为()4,0l 、()4,0l -、()00,y 和()00,y -，其中x 轴上的两个点电荷位置固定，y 轴上的两个点电荷可沿y 轴对称移动（00y ≠），下列说法正确的是（ ）A. 除无穷远处之外，菱形外部电场强度处处不为零B. 当0y 取某值时，可使得菱形内部只存在两个电场强度为零的点C. 当08y l =时，将一带负电的试探电荷由点()4,5l l 移至点()0,3l -，静电力做正功D. 当04y l =时，将一带负电的试探电荷放置在点(),l l 处，其所受到的静电力方向与x 轴正方向成45︒倾斜向上【答案】ACD 【解析】A ．根据场强叠加原理可知，除无穷远处之外，菱形外部电场强度处处不为零，选项A 正确；B ．因为在x 轴上的两个点电荷在O 点的合场强为零，在y 轴上的两电荷，无论y 0取什么值，因为关于原点对称，则在O 点的合场强也为零，在横轴和纵轴上除原点外，出现合场强为零的点，根据对称性可知，一定是成对出现的，关于原点对称，所以算上原点，合场强为零的点是奇数个，不会是2个，选项B 错误；C ．由几何关系可知，坐标为（4l ，5l ）的A 点在第一象限内所在的虚像的垂直平分线的上方；坐标为（0，-3l ）的B 点在第三象限内所在的虚像的垂直平分线的上方，且到达虚线的距离相等，由电势叠加可知，B 点的电势高于A 点，则带负电的试探电荷在A 点的电势能较大，从A 点到B 点电势能减小，可知电场力做正功，选项C 正确；D ．若y 0=4l ，则四个点构成正方形，由对称可知在点（l ，l ）处的场强一定沿着过该点与原点连线的方向上；在y 轴正向和x正向上的点电荷在（l ，l ）处的合场强1222222222255(9)9kql l kq E ll l l l -=⋅=++，在y轴负向和x 负向上的点电荷在（l ，l）处的合场强21213kq E E ==<，可知（l ，l ）点的场强沿着MN 方向且与x 轴从成45︒角的方向向下，将一带负电的试探电荷放置在点(),l l 处，其所受到的静电力方向与x 轴正方向成45︒倾斜向上，选项D 正确．故选ACD ．。

叠加原理实验数据篇一：叠加原理_实验报告范文(含数据处理)叠加原理实验报告一、实验目的验证线性电路偶合原理的正确性，加深对线性电路的认同叠加性和齐次性的认识和理解。

二、原理说明叠加原理指出：在有多个独立源共同作用下的线性电路中，通过每一个元件的电流或其两端的电压，电流看成是时每一个独立源单独作用由在该元件上所所催生的可以或电压的代数和。

线性电路的齐次性是指当激励信号（某独立源的值）增加或减小K 倍时，电路的响应（即在电路中各电阻元件上所建立的电流和电压值）也将增加或减小K倍。

三、实验设备柔性电工技术实验装置DGJ-01：直流稳压电压、直流数字电压表、直流数字电流表、叠加原理实验电子元件DGJ-03。

四、实验步骤1．用实验装置上的DGJ-03线路,按照实验组织协调书上的图3-1，将两路稳压电源的输出分别调节为12V和6V，接入图中的U1和U2处。

2．通过调节开关K1和K2，分别将电源同时作用和单独作用在电路中会，完成如下表格。

表3-13．将U2的数值调到12V，重复以上测量，并记录在表3-1的最后一行中。

4．将R3(330?)换成二极管IN4007，继续测量并填入表3-2中。

表3-2五、实验数据处理和分析对图3-1的线性电路进行理论分析，利用回路电流数据包法或节点电压法列出电路方程，借助计算机进行方程求解，或直接用EWB硬件对电路分析计算，得出的电压、导体的数据与测量值基本相符。

验证了测量数据的准确性。

电压表和电流表的测量有一定的误差，都在可允许的最小值范围内。

验证叠加定理：以I1为例，U1单独作用时，I1a=8.693mA,，U2单独作用时，I1b=-1.198mA，I1a+I1b=7.495mA，U1和U2共同作用时，测量值为7.556mA，因此叠加性亟需验证。

2U2单独作用时，测量值为-2.395mA，而2*I1b=-2.396mA，因此齐次性得以检验。

其他的支路电流和电压也可类似验证叠加定理的准确性。

电路叠加原理电路叠加原理是电路分析中的基本原理之一。

它指出，在只有源一次被激活的情况下，电路中的各元件的电压或电流是可以分别计算的。

这个原理的应用可以帮助我们更加简单、方便地对电路进行分析和设计。

在本篇文章中，我们将探讨电路的叠加原理及其常见应用。

一、电路叠加原理的定义在理解电路叠加原理之前，我们先来看看什么是电路。

电路是由电阻、电容、电感、电源等元件连接而成的，能够实现特定功能的电子系统。

在电路中，每一个元件都有其自身的电流和电压。

而叠加原理指出，在电路中每个元件所受到的电流和电压可以分别计算。

换句话说，我们可以将不同元件产生的电压和电流分别计算，最后汇总成最终结果，这就是电路叠加原理。

二、叠加原理的原理叠加原理的应用基于超额原理。

所谓超额原理是指，在电路分析时，我们可以分别处理每一个源的影响，再将它们分别计算出来，然后把它们加在一起，不考虑其互相影响的结果。

这是因为，每一个电源的作用可以看做只受其本身电量电势的影响，与其他电源或元件的状态无关。

叠加原理的描述可以用克希荷夫定律来简单表示。

根据克希荷夫定律，一条电路中的电流总和等于电源电势和电路中的所有电阻的电压之和。

利用这个原理，我们可以将每个源的电路分离开来，分别求出它们的电流或电压，最终再将它们加在一起，得到整个电路的输入输出特性。

三、叠加原理的应用叠加原理在电路分析中应用非常广泛，下面我们来看看其常见的应用。

1.电压分压器分析应用在分析电路时，常常需要计算不同元件处的电压。

比如，电压分压器中，我们需要计算两端电阻器上的电压。

假设电压分压器中，有两个电源分别加在两个电阻上。

在计算时，我们可以先将一个电源断开，然后将另一个电源中的电压与电阻上的电压相加，以获得该电源产生的总电压。

然后，将这个计算结果与另一个电源的计算结果相加，就可以得到电压分压器的总输出电压了。

2.电阻网络分析应用在分析复杂的电路中，我们常常需要对电阻网络进行分析。

在这种情况下，我们可以使用叠加原理来降低分析复杂度，简化计算。

电势的叠加原理表达式
嘿，朋友们！今天咱们来聊聊电势的叠加原理表达式。

你知道吗，电势就像是一个电场中的“能量标签”！比如说，我们可以把电场想象成一个大舞台（例子：就像演唱会的舞台），而电势就是每个位置独特的标记。

那电势的叠加原理又是什么呢？哇，这可太重要啦！它说的是，当有多个电荷存在时，总的电势就等于每个电荷单独产生的电势加起来呀！这就好像一个乐队演奏（例子：各种乐器发出的声音加在一起），每个乐器都有自己的声音，加在一起就形成了美妙的音乐。

比如说，在一个地方有两个电荷，一个正电荷和一个负电荷。

正电荷会产生自己的电势，负电荷也会。

然后哇，这两者加起来，就是那个地方总的电势啦！这不是神奇得很嘛！（例子：就跟两个人说话，一个人声音大，一个人声音小，我们听到的就是两者混合后的声音）
所以啊，电势的叠加原理表达式真的超级厉害，它让我们能更好地理解和分析电场中的电势分布！明白不啦？哇塞，还不快去更深入地研究一下！。