中学物理竞赛讲义-11.2电势

《电势》讲义一、什么是电势在物理学中，电势是一个非常重要的概念。

简单来说，电势就像是一个“势能的高度”，用来描述电场中某一点所具有的能量性质。

想象一下，在一个山坡上，位置越高的地方，物体所具有的重力势能就越大。

类似地，在电场中，某一点的电势越高，电荷在这一点所具有的电势能就越大。

为了更形象地理解电势，我们可以把电场比作是一个高低不平的“势能场地”。

电荷在这个场地中移动时，其电势能会发生变化，而电势就是用来衡量这个场地中不同位置的势能高低的。

二、电势的定义电势的定义是：把单位正电荷从电场中的某一点移动到参考点（通常取为无穷远处或者大地）时，电场力所做的功。

这个定义可能听起来有点抽象，我们来举个例子。

假设有一个电场，我们要计算其中某一点 A 的电势。

我们把一个单位正电荷从 A 点移动到无穷远处，如果电场力对这个电荷做了 10 焦耳的功，那么 A 点的电势就是 10 伏特。

需要注意的是，电势是一个相对的概念，就像高度一样。

我们说一个地方的高度是多少，总是相对于某个基准面而言的。

在电势中，参考点就是这个基准。

三、电势的单位电势的国际单位是伏特（V），它是以意大利物理学家亚历山德罗·伏特的名字命名的。

1 伏特等于 1 焦耳/库仑。

这意味着，如果在电场中移动 1 库仑的电荷，电场力做了 1 焦耳的功，那么这个位置的电势就是 1 伏特。

除了伏特，在一些特定的情况下，还可能会用到毫伏（mV）、千伏（kV）等单位。

四、电势差电势差是指电场中两点之间电势的差值。

它也被称为电压。

比如说，A 点的电势是 10 伏特，B 点的电势是 5 伏特，那么 A、B 两点之间的电势差就是 5 伏特。

电势差是非常重要的概念，在电路中，电流的产生就是由于存在电势差，电荷在电势差的作用下定向移动，从而形成电流。

五、等势面在电场中，电势相等的点所组成的面叫做等势面。

等势面有一些重要的性质。

首先，等势面与电场线垂直。

这是因为如果不垂直，电场力就会在等势面上做功，这与等势面的定义矛盾。

第11讲 带电物体在电场中的运动1. 电场中的能量2. 自能，互能，电场能本讲的主要例题只是通过带电粒子运动把整个电场一章的内容做一次复习。

知识点睛一.电势能 1.电势能的差静电力是保守力，可引入电势能的概念。

由保守力作功和势能增量的关系有： ΔEp a →b = -(W b - W a )q 0在电场中a 、b 两点电势能之差等于把q 0自a 点移至b 点过程中电场力所作的功。

电势能应属于q 0和产生电场的源电荷系统共有。

2.电势能选标准点(势能零点)，在电场中某点a 的电势能为即把q 0自a →“标准点”的过程中电场力作的功。

所以电势能的定义为：0q E a a p ϕ=3.连续电荷分布的静电能对于一个有限体积的带电体，我们姑且不考虑其微观结构而只注意其静电性质，那么可以说，这一带电体之所以能够结合在一起，是需要外力维持的。

我们设想下面的过程来说明如何构成一个有限大小的带电体。

开始的时候，所有的电荷都位于无穷远处，我们人为地将一个个电荷从无穷远处极缓慢地移动到指定的位置，那么，在这个极缓慢的过程中我们对电荷所施加的力与电荷所受的的静电力想必是大小相等而方向相反的，我们所作的功就应该等于电荷的电势能的增量。

不断地重复这一过程，直到最终组成我们所要的有限大小的带电体，在整个过程中，我们所作的功就是静电体系的静电能。

这样，从功能原理的角度我们重新解释了静电能。

下面通过一个简单的例子来说明书这一过程。

我们来计算一个半径为R 的均匀带电球体的电势能。

现在让我们从功能原理的角度考虑这个问题。

如图所示，为了构造一个半径为R 的带电球体，我们就要准静态地把电荷从无穷远处搬运到适当的位置，并组成球形。

假设在某个时候我们已经构成了如图所示的情形，即已经有了一个半径为r 的带电球体，接下来我们要继续从无穷远处搬运电荷，并将搬来的电荷均匀地分布在这个球体上。

我们每次搬运的电荷都是很少的，设电荷密度为ρ，那么每次搬运的电荷量可以表示为dr rρπ24，而球本讲提纲表面的电势为rr 23441πρπε⋅，无穷远处的电势为零，故在某一次的搬运过程中我们所作的功即为电量为dr r ρπ24的电荷的电势能的改变，它就是dr r rr 2243441πρπρπε⋅⋅最后我们要组成半径为R 的带电球，于是该球体的电势能就是对上式的积分，即dr r rr W R2243441πρπρπε⋅⋅=⎰=41πε522513)4(R ρπ 可以将电荷密度ρ表示为334R Q π，这里Q 是这个球体的带电量，于是上式化为RQ W 204153πε=这便是半径为R 带电量为Q 的均匀球体的静电能。

竞赛专题---电势【知识要点】－电势反映电场能的性质．电场力做功电势能减小，克服电场力做功电势能增加，电势：电场中某点处电荷的电势能‘与它的电量q 之比值叫做场中该点的电势U . 即电势叠加原理：任意带电体电场中某点的电势，等于带电体上各部分电荷单独存在时，在该点产生电势的代数和．电势差：电场中两点电势的差值．若场中 A , B 两点的电势分为ＵＡ，ＵＢ，则两点的电势差记作ＵＡＢ，ＵＡＢ＝ＵＡ－ＵＢ．几种典型电场的电势( l ）点电荷电势如图所示，空间有一点电荷，电量为Q ，先计算AB两点的电势差．设A ,B 到Q 的距离分别为rA , rB ，把检验电荷q 从 A 移到 B 电场力做功为w ，由于是变力做功，不能直接求w ，现把 A 刀分成n段，当n 足够大时，W 可表示为由电势差定义得若以无穷远处为零电势，即把rＢ→∞，ＵＢ＝０．则由于 A 是任意的，所以点电荷的电势为( 2 ）均匀带电球壳电场的电势与场强公式相类似，根据点电荷的电势，可得半径为Ｒ的均匀带电球壳电场的内、外电势分别为【例题分析】例 1 半径分别为Rl 和R２的两个同心球面均匀带电．电荷面密度分别为δ 1 和δ 2 ．试求：( l ）大球面任一直径AB 上的电势分布？( 2 ）如果过AB 将两球各切掉一半，如图9 一 3 一 2 所示，剩下两半球仍均匀带电，电荷面密度不变．直径AB 上的电势分布又如何？分析与解（ 1 ）由均匀带电球壳的电势分布可知：大球面均匀带电，因此它在球内产生的电势处处相等，有小球面均匀带电，它在其球内和球外的电势由电势叠加原理可得：直径AB 上电势分布为( 2 ）当通过直径AB 将两个球面都切去一半时，因为剩下的半球面和切去的半球面相对AB 是对称的，所以剩下的大（小）半球面对直径 A 刀上的电势的贡献仅为完整球面的一半．即直径AB 上的电势分布为例 2 如图9 一 3 一 3 所示，三根等长的细绝缘棒连接成等边三角形，尸点为三角形的内心，Q 点与三角形共面且与尸关于AC 棒对称，三棒带有均匀分布的电荷，此时，测得Ｐ，Q 两点的电势各为ＵＰ，UＱ，现将BＣ棒取走，而AB , AC 棒的电荷分布不变，求这时Ｐ，Q 两点的电势．分析与解由于三棒带有均匀分布的电荷，所以三根棒对Ｐ点电势的贡献应相同，设为Ｕl ．由对称性可知，AＣ对Q 点电势的贡献与它对Ｐ点电势的贡献应相等；BC 和ＢA 对Q点电势的贡献也应相等，设为U２．则电势叠加原理可得由以上两式解得取走BC 棒后，Ｐ，Q 的电势为【巩固习题】1 ．有两个质量分别为ml 和m２的带电相同小球，每个球的电量为Q ，开始时两个小球相距甚远，一个以初速v 向另一个运动，而另一个初速为O ，假定作用在小球上的惟一的力是小球间的静电斥力，求两个小球能接近的最小距离．2 . N 个相同的球形水银液滴，都带有相同的电量，具有相同的电势U ，如果这些水银聚集在一起成一个大的水银滴，这个大水银滴的电势多大？3 ．如图9 一 3 一4 所示，半径为R２的导电球壳包围半径为Rl 的金属球，金属球原来具有电势Ul ．如果让球壳接地，那么金属球的电势变为多少？4 ．正点电荷Ql 和Q２分别置于 A , B 两点，相距为L ，现以L 为直径作半圆，如图9 一 3 一5 所示，试求在此半圆上电势最低点Ｐ的位置，5 一个半径为 a 的孤立的带电金属丝环，其中心处电势为U０．将此环靠近半径为 b 的接地的球，只有环中心点位于球面上，如图9 一 3 一6 ．试求球上感应电荷的电量．6 ．如图9 一 3 一7 所示，点电荷十Q 位于金属球壳的中心，金属球壳的内、外半径分别为Ｒ1 , R２，球壳所带的净电荷为零．若在无限处电势为零，求 A , B 两点的电场强度和电势的大小．7 ．如图9 一 3 一8 所示，半径分别为Rl 与R２的两个同心半球面相对放置，两个半球均匀带电，电荷面密度分别为δ 1 和δ２，试求大的半球面所对应底面直径AOB 上电势分布．8 ．电荷q 均匀分布在半球面ACB 上，球面的半径为R , CD为通过半球顶点 C 与球心O 的轴线，如图9 一 3 一9 所示．Ｐ、Q 为CD 轴线上在O 点两侧．已知Ｐ点的电势为UＰ，离O 点距离相等的两点．试求Q 点的电势U Q ．9 ．如图9 一 3 一10 所示，在真空中有 4 个半径为 a 的不带电的相同导体球，球心分别位于边长为r ( r 》ａ）的正方形的四个顶点上．首先，让球 1 带电荷Q ( Q > 0 ) ，然后取一细金属丝，其一端固定于球 1 上，另一端分别依次与球 2 、 3 、 4 、大地接触，每次接触时间都足以使它们达到静电平衡．设分布在细金属丝上的电荷可忽略不计．试求流人大地的电量的表达式．10 ．两个互相绝缘的同心导体薄球壳，内球壳半径为r１，外球壳半径为r2 ．开始时内球壳带电量为Q ，外球壳不带电．( l ）试求外球壳内、外两个侧面的电荷及外球壳的电势；( 2 ）将外球壳接地后再与地绝缘，计算此时外球壳内、外两侧面的电荷；( 3 ）再将内球壳接地，求此时内球壳的总电量．11 ．点电荷＋Q 附近有一半径为R 的导体球，球心到点电荷Q 的距离为 d ，如图9 –３－１１所示．求：( 1 ）当导体球接地时，感应电荷Q ' ; ( 2 ）当导体球不接地时它的电势U .12 ．真空中，有五个电量均为q 的均匀带电薄球壳，他们的半径分别为R , R / 2 , R / 4 , R / 8 , R / l6 ，彼此内切于Ｐ点，如图9 一 3 一12 所示．球心分别为Ｏ1 , Ｏ2 , Ｏ3 , Ｏ4 ,Ｏ5 ，求Ｏ1 与Ｏ5 间的电势差．。

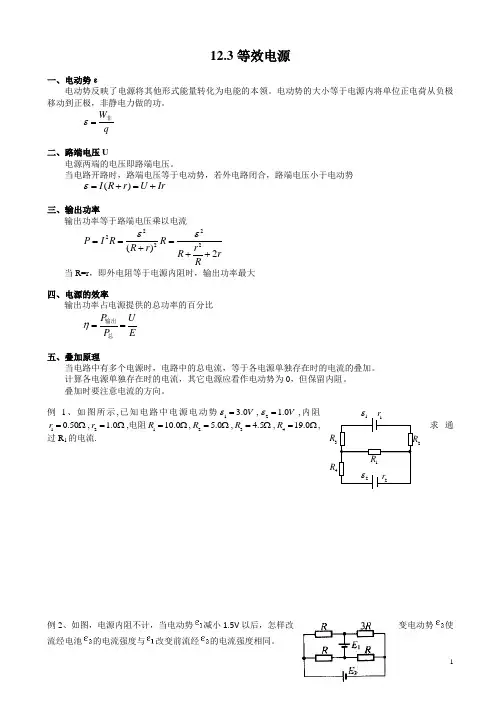
12.3等效电源一、电动势ε电动势反映了电源将其他形式能量转化为电能的本领。

电动势的大小等于电源内将单位正电荷从负极移动到正极，非静电力做的功。

W qε=非二、路端电压U电源两端的电压即路端电压。

当电路开路时，路端电压等于电动势，若外电路闭合，路端电压小于电动势()I R r U Ir ε=+=+三、输出功率输出功率等于路端电压乘以电流22222()2P I R R rR r R r Rεε===+++当R=r ，即外电阻等于电源内阻时，输出功率最大四、电源的效率输出功率占电源提供的总功率的百分比P UP Eη==输出总五、叠加原理当电路中有多个电源时，电路中的总电流，等于各电源单独存在时的电流的叠加。

计算各电源单独存在时的电流，其它电源应看作电动势为0，但保留内阻。

叠加时要注意电流的方向。

例1、如图所示,已知电路中电源电动势1 3.0V ε=,2 1.0V ε=,内阻10.50r =Ω,2 1.0r =Ω,电阻110.0R =Ω,2 5.0R =Ω,3 4.5R =Ω,419.0R =Ω,求通过R 1的电流.例2、如图，电源内阻不计，当电动势减小1.5V 以后，怎样改变电动势使流经电池的电流强度与改变前流经的电流强度相同。

2R R六、等效电源1、等效电压源：两端有源网络可以等效为电压源。

(1)电压源可以看等效电动势和等效内阻串联(2)等效电动势等于网络的开路端电压。

(3)将网络内部电源短路后（保留内阻），两端点之间的等效电阻*2、等效电流源：两端有源网络可以等效为电流源。

(1)电流源可以看等效电动势和等效内阻并联(2)其提供的等效电流等于网络两端短路时的路端电流。

(3)将网络内部电源短路后（保留内阻），两端点之间的等效电阻由于等效电压源和我们通常电源的概念类似，因此常用电压源来解决问题例3、甲乙两个电路中电源电动势ε和内阻r已知，定值电阻R0已知，求电阻R调到多大时，电源输出功率最大？电阻R调到多大时，R上获得的电功率最大？例4、利用等效电压源的方法解决例1如图所示,已知电路中电源电动势13.0Vε=,21.0Vε=,内阻10.50r=Ω,21.0r=Ω,电阻110.0R=Ω,25.0R=Ω,34.5R=Ω,419.0R=Ω,求通过R1的电流.2RR例5、利用等效电压源的方法解决例2如图，电源内阻不计，当电动势减小1.5V以后，怎样改变电动势使流经电池的电流强度与改变前流经的电流强度相同。

《电势》讲义在电学的世界中，电势是一个极其重要的概念。

它就像是一座隐藏在电学现象背后的神秘山峰，等待我们去攀登和探索。

那么，究竟什么是电势呢？简单来说，电势是描述电场中某一点能量性质的物理量。

想象一下，电场就像一个巨大的力场，而电势则告诉我们在这个力场中不同位置所具有的“能量高度”。

为了更形象地理解电势，我们可以把电场比作一个山坡。

在山坡上，位置越高，物体所具有的重力势能就越大。

同样，在电场中，电势越高的地方，电荷所具有的电势能也就越大。

要深入理解电势，我们还需要了解电势差。

电势差，也被称为电压，它是指两点之间电势的差值。

比如，我们常见的电池，其两端就存在电势差，正是这个电势差驱动了电荷的定向移动，从而形成了电流。

那电势是怎么测量的呢？在实际中，我们通常把大地或者无限远处的电势规定为零。

然后，通过测量其他点相对于这个零点的电势差，来确定该点的电势。

让我们来思考一个例子。

假设有一个带正电的点电荷，它周围会产生电场。

离这个点电荷越近的地方，电势就越高；离得越远，电势就越低。

这是因为正电荷会产生向外的电场，把正电荷从近处移动到远处，电场力做正功，电势能减小，电势降低。

再来说说等势面。

等势面是指电场中电势相等的点所组成的面。

等势面与电场线是垂直的。

为什么呢？因为如果不垂直，沿着等势面移动电荷时，电场力就会做功，这与等势面的定义相矛盾。

在实际应用中，电势的概念有着广泛的用途。

比如在电子电路中，我们需要了解不同点的电势，以确保电路的正常工作。

在静电学中，通过分析电势分布，可以计算出电场的强度和方向。

电势的概念还与电容器密切相关。

电容器是储存电荷和电能的器件，电容器两极板之间存在电势差。

当电容器充电时，两极板上的电荷逐渐增加，电势差也随之增大；当电容器放电时，电荷减少，电势差减小。

总之，电势是电学中一个非常基础且重要的概念。

它不仅帮助我们理解电荷在电场中的能量状态，还为我们分析和解决各种电学问题提供了有力的工具。

《电势》讲义在物理学中，电势是一个非常重要的概念。

它就像是一个隐藏在电学世界背后的神秘力量，虽然看不见摸不着，但却对电荷的运动和电现象起着至关重要的作用。

接下来，让我们一起揭开电势的神秘面纱，深入了解它的本质和特性。

一、什么是电势简单来说，电势就是描述电场中某一点能量性质的物理量。

想象一下，电场就像是一个有高低起伏的“能量场”，而电势就好比是这个场中各个点的“高度”。

电荷在电场中会受到力的作用而移动，而电势的差异决定了电荷移动的方向和趋势。

更具体地讲，如果把一个正电荷从电场中的一点移动到另一点，电场力对它做了功，那么这两点之间就存在电势差。

电势差的大小等于单位正电荷从一点移动到另一点时电场力所做的功。

为了更形象地理解电势，我们可以打个比方。

把电场比作一个山坡，电势高的地方就像是山顶，电势低的地方就像是山脚。

正电荷就像一个小球，它总是会从山顶（电势高的地方）滚向山脚（电势低的地方）。

二、电势的单位在国际单位制中，电势的单位是伏特（V）。

1 伏特的定义是：将 1 库仑的正电荷从一点移动到另一点，如果电场力做了 1 焦耳的功，那么这两点之间的电势差就是 1 伏特。

伏特这个单位是为了纪念意大利物理学家亚历山德罗·伏特而命名的。

三、电势的计算计算电势需要用到一些特定的公式和方法。

对于一个点电荷产生的电场，在距离点电荷 r 处的电势可以用公式V ＝ kQ/r 来计算，其中 k 是库仑常量，Q 是点电荷的电荷量。

如果是多个点电荷组成的电场，或者是一个连续分布的电荷所产生的电场，计算电势就需要用到积分的方法。

这可能会涉及到比较复杂的数学运算，但基本的原理仍然是根据电场力做功来确定电势差。

四、等势面等势面是电势相等的点所组成的面。

等势面有以下几个重要的性质：1、等势面与电场线垂直。

这是因为电场线的方向表示电场强度的方向，而电场强度总是沿着电势降低最快的方向。

2、相邻等势面之间的电势差相等。

3、不同的等势面不会相交。

电势能和电势一、静电力做功与电势能的变化 1．静电力做功和特点：静电力对电荷做的功只与电荷的起始位置和终止位置有关，而与电荷经过的路径无关。

这一点跟重力做功很相似．说明：这一结论在匀强电场中适用，在非匀强电场中也适用。

2．电势能：定义：电荷在电场中具有的能叫做电势能，用Ep 表示． 单位：焦耳， 是标量． 3．静电力做功与电势能变化的关系：静电力对电荷做了功，电势能就发生了变化，静电力对电荷做了多少功，就有多少电势能转化为其他形式的能，电荷克服静电力做了多少功，就有多少其他形式的能转化为电势能．也就是说，静电力做功是电势能转化为其他形式的能的度量，所以： 静电力做功等于电势能的减少量，即pB pA AB E E W -=静电力做正功，电势能一定减少，静电力做负功，电势能一定增加． 4．电势能的大小．电势能是标量，电势能的大小是相对于参考位置来说的，（所谓参考位置就是电势能为零的位置）参考位置的选取是任意的，通常取无限远处或大地为参考点，即电势能零点，设电荷在电场中某点A 的电势能为E p A ，移动到参考点O 时电场力做功W AO ，则W AO ＝E p A －E p O ，若规定O 点为参考点就有E p O ＝0，则：E p A ＝W AO所以：电荷在某点的电势能等于把它从这点移动到零势能点位置时电场力做的功。

5．重力势能与电势能的比较．例1：右图中MN 为电场中某一条电场线方向向右，在线取两点a 、b 今将一电荷＋q 从a 移到b 则（ ）重力势能电势能重力做功与路径无关，只与始末位置有关静电力做功与路径无关，只与始末位置有关重力做正功，重力势能减小．重力做负功，重力势能增加静电力做正功，电势能减小．静电力做负功，电势能增加重力势能的数值具有相对性，可以为正值，可以为负值，也可以为零 电势能的数值具有相对性，可以为正，可以为负，也可以是零 重力势能是标量电势能是标量A.电场力做正功，＋q的电势能增加；B.电场力做负功，＋q的电势能增加；C.电场力做正功，＋q的电势能减少；D.电场力做负功，＋q的电势能减少。

11.2电势一、电势叠加原理某点的总电势等于各场源电荷在该点产生的电势的标量和。

二、几种常见电场的电势1、距离点电荷 r 处的电势（微元法证明）rkQ =ϕ2、半径为R 的均匀带电薄球壳 壳外：rkQ =ϕ 壳内：R kQ =ϕ例1、（1）解释：接触起电中电量均分定理的适用条件为两个小球完全相同。

（2）解释：不规则导体，尖的部位电荷面密度较大。

例2、求带电量为Q ，半径为R 的均匀带电细环在圆心处的电势例3、半径为R 2的不带电导体球壳包围半径为R 1的带电金属球，金属球具有电势U 1。

如果让球壳接地。

那么金属球的电势变为多少？例4、一个半径为a 的孤立带电金属丝环，其中心处电势为U 0，将此球靠近圆心为O 1、半径为b 的接地的导体球，只有环中心O 位于球面上，如图所示，试求球上感应电荷的电量。

例5、如图所示，两个同心导体球，内球半径为R 1，外球是个球壳，内半径为R 2，外半径R 3.在下列各种情况下求内外球壳的电势差以及壳内空腔和壳外空间的电势分布规律.（1）内球带q +，外球壳带Q +.（2）内球带q +，外球壳不带电.（3）内球带q +，外球壳不带电且接地.（4）内球通过外壳小孔接地，外球壳带Q +.b a O O 1例6、如图所示，O 为半径等于R 的原来不带电的导体球的球心，O 1、O 2、O 3为位于球内的三个半径皆为r 的球形空腔的球心，它们与O 共面，已知2321R OO OO OO ===．在OO 1、OO 2的连线上距O 1、O 2为2r 的P 1、P 2点处分别放置带电量为q 1和q 2的线度很小的导体（视为点电荷），在O 3处放置一带电量为q 3的点电荷，设法使q 1、q 2和q 3固定不动．在导体球外的P 点放一个电量为Q 的点电荷，P 点与O 1、O 2、O 3共面，位于O O 3的延长线上，到O 的距离R OP 2=．1．求q 3的电势能． 2．将带有电量q 1、q 2的小导体释放，当重新达到静电平衡时，各表面上的电荷分布有何变化？ 此时q 3的电势能为多少？二、电像法比较等量异种点电荷周围的电场和点电荷与接地导体板周围的电场。