棱柱和棱锥(中职数学)

棱柱棱台棱锥知识点总结一、棱柱的定义和性质1. 棱柱的定义：棱柱是一个多边形和一个平行于它的平面所围成的几何图形。

2. 棱柱的特征：（1）棱柱的底面是一个多边形，顶面与底面平行，并且顶面的每个点和底面的对应点之间的连线都垂直于底面。

（2）如果底面是正多边形，棱柱就称为正棱柱；如果底面是不规则多边形，棱柱就称为斜棱柱。

（3）棱柱的高等于顶面到底面的距离，底面的面积乘以高就是棱柱的体积。

二、棱台的定义和性质1. 棱台的定义：棱台是由平行多边形和连通它们的矩形棱所围成的空间图形。

2. 棱台的特征：（1）如果底面和顶面都是正多边形，且它们的对边平行，那么这个棱台称为正棱台；如果底面和顶面是正多边形，但它们不一定平行，那么这个棱台称为斜棱台。

（2）棱台的体积等于底面积与高的乘积，而斜棱台的体积还需要乘以一个高与底面中较大边的比值。

三、棱锥的定义和性质1. 棱锥的定义：棱锥是由一个多边形和以它为底的三棱锥棱所围成的几何图形。

2. 棱锥的特征：（1）如果底面是正多边形，棱锥称为正棱锥；如果底面不是正多边形，那么棱锥就称为斜棱锥。

（2）棱锥的体积等于底面积与高的乘积，并除以3。

（3）棱锥的侧棱的延长线与底面平面的交点称为顶点。

四、棱柱、棱台、棱锥的计算公式1. 棱柱的体积公式：V=Sh，其中V表示棱柱的体积，S表示底面的面积，h表示高。

2. 棱台的体积公式：V=(S1+S2+√S1S2)h/3，其中V表示棱台的体积，S1和S2表示底面和顶面的面积，h表示高。

3. 棱锥的体积公式：V=Sh/3，其中V表示棱锥的体积，S表示底面的面积，h表示高。

以上就是关于棱柱、棱台、棱锥的知识点总结，希望对你有所帮助。

如果还有其他问题，欢迎继续提问。

数学中的棱柱与棱锥的性质数学中，棱柱与棱锥是常见的立体几何形体。

它们具有一些独特的性质和特点，对于理解和运用立体几何知识都至关重要。

本文将会介绍棱柱和棱锥的定义、性质以及相关的应用。

一、棱柱的定义和性质1. 定义：棱柱是由两个平行且相等的底面，以及连接底面上对应顶点的若干条棱所组成的立体形体。

2. 性质：（1）棱柱的侧面是由若干条相互平行的线段所组成，这些线段被称为棱。

（2）棱柱的底面是多边形，其边数与侧面棱数相同，并相互平行。

（3）棱柱的高是两个底面之间的垂直距离。

（4）棱柱的体积可以通过底面积和高的乘积计算得到。

二、棱锥的定义和性质1. 定义：棱锥是由一个多边形底面和连接底面顶点与一个非在同一平面上的点的棱所组成的立体形体。

2. 性质：（1）棱锥的侧面是由底面的边和连接底面顶点与顶点的棱组成。

（2）棱锥的底面是一个多边形。

（3）棱锥的高是从顶点到底面的垂直距离。

（4）棱锥的体积可以通过底面积和高的乘积再除以3计算得到。

三、棱柱和棱锥的应用1. 棱柱的应用：（1）柱体的形状多用于建筑设计，比如柱子、烟囱等。

（2）在计算几何中，柱体的体积计算可以应用到计算物体的容积、质量等问题中。

2. 棱锥的应用：（1）锥体的形状常见于圆锥、塔尖等建筑物的设计。

（2）在几何学和几何光学中，锥体的性质和转光性质有着重要的应用。

总结：通过对数学中棱柱和棱锥的定义、性质以及应用进行了介绍，我们可以更好地理解和运用立体几何知识。

棱柱和棱锥的独特性质和计算方法有助于解决实际问题，并在建筑设计、几何学、几何光学等领域得到广泛应用。

掌握和理解棱柱和棱锥的概念，对于数学学习和应用具有重要意义。

认识数学中的棱柱与棱锥体积数学是一门抽象而又实用的学科，它贯穿于我们日常生活的方方面面。

在数学的世界中，有许多有趣的几何概念，其中包括棱柱和棱锥体积。

本文将详细介绍这两个概念，让我们一起来认识数学中的棱柱与棱锥体积。

一、棱柱的概念与性质棱柱是由两个平行且相等的多边形底面以及连接底面对应顶点的直线段组成的几何体。

棱柱的体积可以通过以下公式来计算：V = 底面积 ×高其中，底面积是指底面的面积，高是指连接底面的直线段的长度。

棱柱的底面可以是任意多边形，例如三角形、四边形或者正多边形。

棱柱的侧面可以看作是底面上的边与连接底面顶点的直线段所围成的区域。

棱柱的体积计算方法可以通过一个简单的例子来理解。

假设有一个底面积为10平方厘米，高为5厘米的三角形棱柱，那么它的体积可以计算如下：V = 10平方厘米 × 5厘米 = 50立方厘米从上述例子可以看出，棱柱的体积与底面积以及高密切相关。

当底面积或高增加时，棱柱的体积也会相应增加。

二、棱锥的概念与性质棱锥是由一个多边形底面和连接底面顶点与一个点的直线段组成的几何体。

棱锥的体积可以通过以下公式来计算：V = 1/3 ×底面积 ×高其中，底面积指的是底面的面积，高是指连接底面顶点与顶点的直线段的长度。

棱锥的底面可以是任意多边形，例如三角形、四边形或者正多边形。

棱锥的侧面可以看作是底面上的边与连接底面顶点与顶点的直线段所围成的区域。

为了更好地理解棱锥的体积计算方法，我们可以举一个实际的例子。

假设有一个底面积为8平方厘米，高为6厘米的三角形棱锥，那么它的体积可以计算如下：V = 1/3 × 8平方厘米 × 6厘米 = 16立方厘米从上述例子可以看出，棱锥的体积与底面积以及高的关系也是密切相关的。

当底面积或高增加时，棱锥的体积也会相应增加。

三、棱柱与棱锥体积的比较通过对棱柱和棱锥体积的计算公式进行比较，我们可以发现它们之间存在着明显的差异。

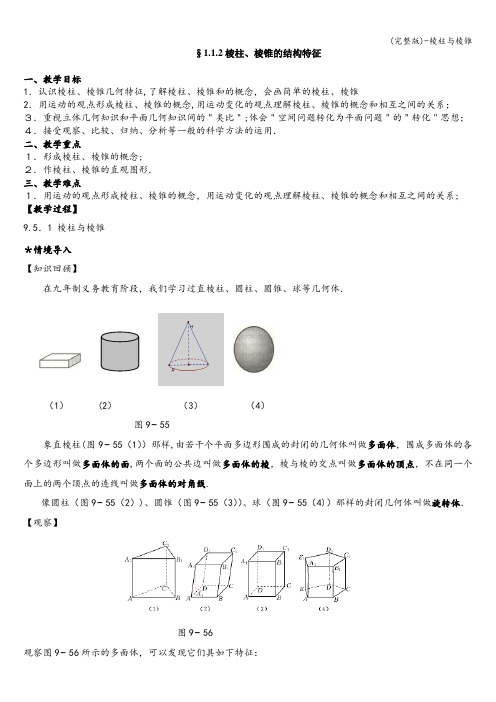
§1.1.2棱柱、棱锥的结构特征一、教学目标1．认识棱柱、棱锥几何特征,了解棱柱、棱锥和的概念，会画简单的棱柱、棱锥2．用运动的观点形成棱柱、棱锥的概念,用运动变化的观点理解棱柱、棱锥的概念和相互之间的关系；３．重视立体几何知识和平面几何知识间的＂类比＂;体会＂空间问题转化为平面问题＂的＂转化＂思想；４．接受观察、比较、归纳、分析等一般的科学方法的运用．二、教学重点１．形成棱柱、棱锥的概念;２．作棱柱、棱锥的直观图形．三、教学难点１．用运动的观点形成棱柱、棱锥的概念，用运动变化的观点理解棱柱、棱锥的概念和相互之间的关系;【教学过程】9.5．1 棱柱与棱锥＊情境导入【知识回顾】在九年制义务教育阶段，我们学习过直棱柱、圆柱、圆锥、球等几何体．（1） (2）（3）（4）图9−55象直棱柱(图9−55（1））那样,由若干个平面多边形围成的封闭的几何体叫做多面体，围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱，棱与棱的交点叫做多面体的顶点，不在同一个面上的两个顶点的连线叫做多面体的对角线.像圆柱（图9−55（2）)、圆锥（图9−55（3））、球（图9−55（4)）那样的封闭几何体叫做旋转体．【观察】图9−56观察图9−56所示的多面体，可以发现它们具如下特征：(1）有两个面互相平行，其余各面都是四边形；（2）每相邻两个四边形的公共边互相平行．＊引入新知有两个面互相平行，其余每相邻两个面的交线都互相平行的多面体叫做棱柱，互相平行的两个面，叫做棱柱的底面,其余各面叫做棱柱的侧面．相邻两个侧面的公共边叫做棱柱的侧棱．两个底面间的距离，叫做棱柱的高．根据棱柱的底面可以是三角形、四边形、五边形等这样的棱柱叫做三棱柱、四棱柱、五棱柱等图9−56所示的四个多面体都是棱柱．表示棱柱时，通常分别顺次写出两个底面各个顶点的字母，中间用一条短横线隔开，例如，图9−56（2）所示的棱柱，可以记作棱柱1111ABCD A B C D -，或简记作棱柱1AC ．经常以棱柱底面多边形的边数来命名棱柱,如图9−56所示的棱柱依次为三棱柱、四棱柱、五棱柱． 侧棱与底面斜交的棱柱叫做斜棱柱，如图9−56（2);侧棱与底面垂直的棱柱叫做直棱柱，如图9−56（1）；底面是正多边形的直棱柱叫做正棱柱，如图9−56(3)和（4），分别为正四棱柱和正五棱柱．正棱柱有下列性质：（１)侧棱垂直于底面，各侧棱长都相等，并且等于正棱柱的高；（２）两个底面中心的连线是正棱柱的高．例1。

棱柱与棱锥的概念与计算在几何学中，棱柱和棱锥是两个常见的三维几何体。

它们具有不同的形状和特点，并且在计算其面积和体积时需要使用不同的公式。

一、棱柱的概念与计算棱柱是一种具有两个相等且平行的底面的几何体。

其侧面由若干个矩形组成，而底面则是由相等的多边形构成。

棱柱的名字通常根据底面的形状来命名，例如正方形棱柱、长方形棱柱等。

棱柱的计算主要涉及到面积和体积的计算。

下面将介绍一些常用的计算公式。

1. 底面积（B）：棱柱的底面积可以根据底面的形状来计算。

例如，正方形底面的棱柱的底面积可以用公式B = 边长^2来计算。

2. 侧面积（S）：棱柱的侧面积是指所有侧面的总和。

对于矩形侧面，可以用长乘以宽来计算。

因此，棱柱的侧面积可以用公式S = 周长 ×高来计算。

3. 总面积（A）：棱柱的总面积是指所有面积的总和。

可以用底面积加上两倍的侧面积来计算。

公式为A = 2B + S。

4. 体积（V）：棱柱的体积可以通过将底面积乘以高来计算。

因此，公式为V = B ×高。

二、棱锥的概念与计算棱锥是一种具有一个底面和一个顶点的几何体。

棱锥的侧面由多个三角形组成，而底面则可以是不规则的多边形。

和棱柱一样，棱锥的名字也通常根据底面的形状来命名，例如正三角锥、正四边锥等。

棱锥的计算也涉及到面积和体积的计算。

下面介绍一些常用的计算公式。

1. 底面积（B）：棱锥的底面积可以根据底面的形状来计算。

例如，正三角形底面的棱锥的底面积可以使用公式B = (边长 ×高) / 2来计算。

2. 侧面积（S）：棱锥的侧面积是指所有侧面的总和。

对于三角形侧面，可以使用海伦公式来计算面积，然后将其累加。

因此，棱锥的侧面积可以用公式S = ∑(边长 ×半周长)来计算。

3. 总面积（A）：棱锥的总面积是指底面积加上所有侧面积的总和。

公式为A = B + S。

4. 体积（V）：棱锥的体积可以通过将底面积乘以高再除以3来计算。

(完整版)棱柱和棱锥的知识点整理棱柱和棱锥的知识点整理
棱柱和棱锥是几何学中常见的几何体，它们具有一些独特的特
性和属性。

以下是对棱柱和棱锥的知识点的整理：
棱柱
- 棱柱是由两个平行的底面和连接底面的若干个直线段（棱）
所构成的几何体。

- 底面是具有相同形状和大小的平面，棱连接底面上对应点的
直线段。

- 棱柱的侧面是由棱和底面组成的平面形成的。

- 棱柱的顶面是连接棱的顶点的平面。

- 棱柱有一个轴线，通过底面中心和顶面中心的直线叫做轴线。

棱锥
- 棱锥是由一个底面和连接底面到一个顶点的直线段（棱）所
构成的几何体。

- 底面是一个平面形状，棱连接底面上点到顶点的直线段。

- 棱锥的侧面是由棱和底面组成的平面形成的。

- 棱锥的顶面是连接棱的顶点的平面。

相似性质
- 棱柱和棱锥都是由底面和侧面组成的几何体。

- 棱柱和棱锥的侧面都是由棱和底面组成的平面形成的。

- 棱柱和棱锥都有一个顶点，并且顶点连接底面上对应点的直
线段。

- 棱柱和棱锥都有轴线，轴线通过底面中心和顶面中心的直线。

以上是对棱柱和棱锥的基本知识点的整理。

它们是几何学中重
要的几何体，应用广泛，在日常生活和工作中都可以看到它们的存在。

参考资料：
- 《高中几何与初等数学教材》
- 《几何与拓扑》。

棱柱与棱锥的认识与分类棱柱和棱锥是几何图形中的重要概念。

它们是立体几何中常见的形状，具有不同的特征和属性。

本文将对棱柱和棱锥进行认识与分类的介绍，帮助读者更好地理解这两种几何形状。

一、棱柱的认识与分类棱柱是由两个相似的多边形底面和连接这两个底面的矩形侧面组成的立体。

它的特点是侧面是平行于底面的矩形，并且棱柱的顶点到底面的距离都相等。

我们可以根据棱柱底面的形状来对棱柱进行分类。

1. 正棱柱：当底面为正多边形（如正三角形、正方形等）时，棱柱称为正棱柱。

正棱柱的特点是底面的边和侧面的高线垂直，并且侧面也是正多边形。

2. 直棱柱：当底面为任意多边形时，棱柱称为直棱柱。

直棱柱的特点是底面的边和侧面的高线不一定垂直，而是可以偏离垂直方向。

3. 斜棱柱：如果棱柱的侧面倾斜，则称为斜棱柱。

斜棱柱的特点是底面的边和侧面的高线不垂直，而是有倾斜的角度。

二、棱锥的认识与分类棱锥是由一个多边形底面和连接底面每个顶点至一个共同点（顶点）的三角形侧面组成的立体。

棱锥的特点是它只有一个顶点，而其它顶点都在该顶点到底面的连线上。

我们可以根据底面的形状来对棱锥进行分类。

1. 正棱锥：当底面为正多边形时，棱锥称为正棱锥。

正棱锥的特点是底面的边和侧面的斜高线垂直，并且侧面也是正多边形。

2. 直棱锥：当底面为任意多边形时，棱锥称为直棱锥。

直棱锥的特点是底面的边和侧面的斜高线不一定垂直，而是可以偏离垂直方向。

3. 斜棱锥：如果棱锥的侧面倾斜，则称为斜棱锥。

斜棱锥的特点是底面的边和侧面的斜高线不垂直，而是有倾斜的角度。

三、棱柱与棱锥的区别与联系棱柱和棱锥在形状上有一定的类似之处，都是由底面和侧面组成的立体。

但是它们的区别主要体现在以下几个方面：1. 顶点数量：棱柱有两个底面，而棱锥只有一个底面，顶点是唯一的。

2. 侧面形状：棱柱的侧面是矩形，而棱锥的侧面是三角形。

棱柱的侧面可以是正多边形或任意多边形，而棱锥的侧面也可以是正多边形或任意多边形。