棱柱+棱锥-高中数学专题复习
- 格式:doc
- 大小:2.03 MB
- 文档页数:13
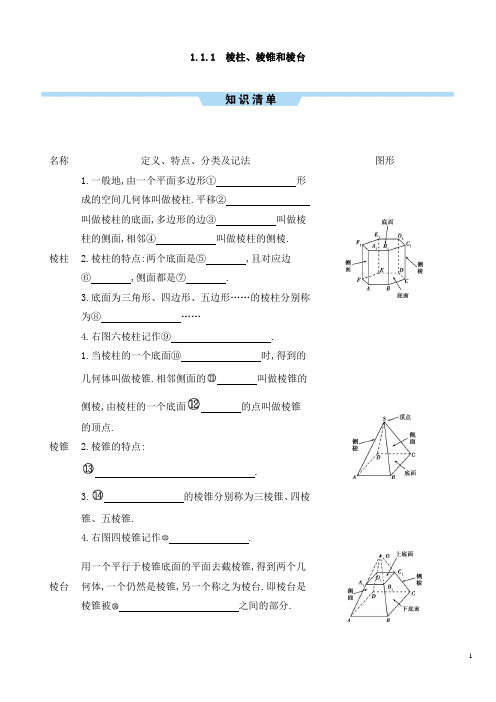
1.1.1 棱柱、棱锥和棱台名称定义、特点、分类及记法图形棱柱 1.一般地,由一个平面多边形① 形成的空间几何体叫做棱柱.平移② 叫做棱柱的底面,多边形的边③ 叫做棱柱的侧面,相邻④ 叫做棱柱的侧棱.2.棱柱的特点:两个底面是⑤ ,且对应边⑥ ,侧面都是⑦ .3.底面为三角形、四边形、五边形……的棱柱分别称为⑧ ……4.右图六棱柱记作⑨ .棱锥 1.当棱柱的一个底面⑩ 时,得到的几何体叫做棱锥.相邻侧面的 叫做棱锥的侧棱,由棱柱的一个底面 的点叫做棱锥的顶点.2.棱锥的特点:. 3.的棱锥分别称为三棱锥、四棱锥、五棱锥.4.右图四棱锥记作 .棱台 用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个仍然是棱锥,另一个称之为棱台.即棱台是棱锥被 之间的部分.多面体1.棱柱、棱锥和棱台都是由围成的几何体.2.叫做多面体.3.多面体有几个面就称为几面体,如三棱锥是.一、填空题1.下列几何体中, 是棱柱, 是棱锥, 是棱台.2.下列命题中正确的序号是.①棱柱的底面一定是平行四边形;②棱柱的底面一定是三角形;③棱锥被截面分成的两部分不可能都是棱锥;④棱柱被平面分成的两部分可以都是棱柱.3.一个棱柱至少有个面.4.将梯形沿某一方向平移形成的几何体是.5.一个棱锥被平行于底面的平面所截,若截面面积与底面面积之比为4∶9,则此棱锥的侧棱被分成上、下两部分之比为.6.不在同一个面上的两个顶点的连线叫做棱柱的体对角线,则六棱柱有条体对角线.7.如图,三棱台ABC A'B'C',沿A'BC截去三棱锥A'ABC,则剩余部分是.①四棱锥;②四棱台;③三棱柱;④三棱锥.8.将图中所给出的平面图形,按虚线折痕折起并黏合,制作成几何体.你能说出得到的几何体的名称吗?请填在对应的横线上.二、解答题9.画一个三棱台,再把它分成:(1)一个三棱柱和另一个多面体;(2)三个三棱锥,并用字母表示.10.甲乙两足球队决赛互罚点球时,罚球点离球门约10米,乙队守门员违例向前冲出3米,因而扑住了点球,不光彩地赢得了比赛.事实上,乙队守门员违例向前冲出了3米后,其要封堵的区域面积变小了.问此时乙队守门员需封堵的区域面积与原来球门的面积的比是多少?11.如图,在正方体ABCD A1B1C1D1各顶点处割去一个三棱锥,使三棱锥的底面三角形的顶点为正方体各棱的中点(例如顶点A1处割去了三棱锥A1EFG,E、F、G分别为A1A、A1B1、A1D1的中点),试问所得到的几何体有多少个面?多少个顶点?多少条棱?知识清单①沿某一方向平移②起止位置的两个面③平移所形成的面④侧面的公共边⑤全等的多边形⑥互相平行⑦平行四边形⑧三棱柱、四棱柱、五棱柱⑨六棱柱ABCDEF-A1B1C1D1E1F1⑩收缩为一个点公共边收缩而成底面是多边形,侧面是有一个公共顶点的三角形底面为三角形、四边形、五边形四棱锥S-ABCD平行于底面的一个平面所截后,截面和底面一些平面多边形由若干个平面多边形围成的几何体四面体基础过关一、填空题1.答案①③④;⑥;⑤解析由棱柱、棱锥和棱台的定义知,①③④符合棱柱的定义;②是一个三棱柱被截去了一部分;⑤符合棱台的定义;⑥符合棱锥的定义.故①③④是棱柱,⑥是棱锥,⑤是棱台.2.答案④解析根据棱柱、棱锥的几何特征作图判断可得答案.3.答案 5解析根据定义知底面边数最少的棱柱是三棱柱,有5个面.4.答案四棱柱解析多边形平移形成的几何体是棱柱,梯形是四边形.故填四棱柱.5.答案2∶1解析截得的小棱锥与原棱锥的侧棱之比为2∶3,故此棱锥的侧棱被分成上、下两部分之比为2∶1.6.答案18解析画出六棱柱,按照顺序找出体对角线,共18条.7.答案①解析在题图中,截去三棱锥A'-ABC后,剩余的是以四边形BCC'B'为底面,A'为顶点的四棱锥.8.答案(1)四棱柱(2)三棱柱(3)六棱柱(4)四棱柱(5)三棱锥(6)四棱锥(7)正方体(8)八面体(9)四棱台解析求解此类题目的关键是要熟悉各种几何体的结构特征.有条件的可以用硬纸卡片进行折叠操作.二、解答题9.解析(1)如图①所示,三棱柱AB2C2A1B1C1与另一个多面体.(2)如图②所示,三个三棱锥分别是A1ABC,B1A1BC,C1A1B1C.图①图②10.解析从罚球点S向球门ABCD四个角引线,构成四棱锥S ABCD(如图),守门员从平面ABCD向前移动3米至平面A'B'C'D',只需封堵A'B'C'D'即可,故S A'B'C'D'S ABCD =(710)2=49100.11.解析正方体原来有6个面,现在8个顶点都被割去,因此增加了8个面,这样所得到的几何体一共有14个面;它的棱数正好是8个三角形边数之和,所以一共有24条棱;每个顶点引出了4条棱,但一条棱连着两个顶点,设顶点数为V,则有4V2=24,即V=12.故所得到的几何体一共有14个面,12个顶点,24条棱.。


高二数学棱柱、棱锥和棱台【本讲主要内容】棱柱、棱锥和棱台棱柱的概念及性质、棱锥的概念及性质和棱台的概念及性质【知识掌握】 【知识点精析】1. 棱柱的有关概念和性质。
(1)棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫做棱柱。
(2)棱柱的几个概念。
这里,两个互相平行的面叫做棱柱的底面,其余各面叫做棱柱的侧面;两个面的公共边叫做棱柱的棱,其中两个侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点,不在同一个面内的两个顶点的连线叫做棱柱的对角线,两个底面的距离叫做棱柱的高。
(3)棱柱的表示方法:棱柱用表示底面各顶点的字母来表示,如三棱柱ABC A B C -111(4)棱柱的分类。
棱柱按底面边数可以分为三棱柱、四棱柱、五棱柱…… 按侧面与地面是否垂直,棱柱又可以分为直棱柱和斜棱柱。
底面是正多边形的直棱柱叫做正棱柱。
正棱柱是特殊的直棱柱。
(5)棱柱的性质: ①侧棱都相等;②侧面都是平行四边形;③两个底面与平行于底面的截面是全等的多边形;④过不相邻的两条侧棱的截面是平行四边形。
平行六面体:底面是平行四边形的四棱柱; 直平行六面体:侧棱与底面垂直的平行六面体; 长方体:底面是矩形的直平行六面体; 正方体:棱长都相等的长方体叫做正方体。
四棱柱与特殊的平行六面体有如下关系:{正方体}⊂{正四棱柱}⊂{长方体}⊂{直平行六面体}⊂{平行六面体}⊂{四棱柱} 长方体的性质:长方体的一条对角线的长的平方等于一个顶点上三条棱长的平方和。
2. 棱锥的有关概念。
(1)棱锥的定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,这些面围成的几何体叫做棱锥。
(2)棱锥的几个概念。
这个多边形叫做棱锥的底面,其余各面叫做棱锥的侧面,相邻侧面的公共边叫做棱锥的侧棱,各侧面的公共顶点叫做棱锥的顶点,顶点到底面的距离叫做棱锥的高。
(3)棱锥的表示方法:棱锥用表示顶点和底面各顶点,或者底面一条对角线端点的字母来表示,如棱锥S -ABCDE ,或者棱锥S -AC 。


棱柱和棱锥一、选择题1.若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是 ( ) (A )三棱锥 (B )四棱锥 (C )五棱锥 (D )六棱锥 [答案]D[解析]提示:正六边型对角线为边长的两倍2.A 1B 1C 1-ABC 是直三棱柱,∠BCA=900,点D 1,F 1分别是A 1B 1,A 1C 1的中点.若BC=CA=CC 1,则BD 1与AF 1所成角的余弦值是 ( )(A )1030(B )21 (C )1530 (D )1015[答案]A[解析]取BC 中点G ,连结G F 1结, 则G F 1与BD 1平行,再连结AG ,在三角形AG F 1中计算即得. 3.在正三棱柱ABC —A 1B 1C 1中,若AB =2BB 1,则AB 1与C 1B 所成的角的大小为A 、60°B 、90°C 、105°D 、75° [答案]B[解析]取AB ,BB 1,B 1C 1中点EFG ,计算可得边长分别为2,2,2, 4.已知三棱锥D-ABC 的三个侧面与底面全等,且AB=AC=3,BC=2,则以BC 为棱,以面BCD 与面BCA为面的二面角的大小是( ) (A )33arccos (B )31arccos (C )2π (D )32π[答案]C[解析]取BC 中点E .连结AE ,DE ,三角形ADE 中计算即得. 5.将边长为a 的正方形ABCD 沿对角线AC 折起,使得BD=a ,则三棱锥D-ABC 的体积为( )(A )63a (B )123a (C )3123a (D )3122a[答案]D[解析]取AC 中点E ,则三角形BDE 面积为24a ,AC 与三角形BDE 面积得乘积得三分之一即为三棱锥D-ABC 的体积.6.在三棱锥A —BCD 中,P 、Q 分别是棱AC 、BD 上的点,连AQ 、CQ 、BP 、DP 、PQ ,若三棱锥A —BPQ 、B —CPQ 、C —DPQ 的体积分别为6、2、8,则三棱锥A —BCD 的 体积是 ( )A .20B .28C .40D .88[答案]C[解析] 三棱锥A —BPQ 的体积为6*4=24,所以三棱锥A —BCD 的体积为6+24+2+8=407.正三棱锥底面边长为a ,侧棱与底面所成角为60°,过底面一边作一截面使其与底面成30°的二面角,则此截面面积为 ( )A .243a B .231a C .283a D .以上答案都不对[答案]C[解析]取此边的中点,则截面的高与此边的所对的底面顶点成一角为30°的直角三角形,故截面的高长34a ,故截面面积为283a 8.已知三棱锥ABC P -中,顶点P 在底面的射影O 是三角形ABC 的内心,关于这个三棱锥有三个命题:①侧棱PC PB PA ==;②侧棱PC PB PA 、、两两垂直;③各侧面与底面所成的二面角相等.其中错误的是 ( )(A )①② (B )①③ (C )②③ (D )①②③ [答案]A[解析]内心到三边的距离相等,故③正确9.如果三棱锥S-ABC 的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点S 在底面的射影O 在△ABC 内,那么O 是△ABC 的 ( ) (A )垂心 (B )重心 (C )外心 (D )内心 [答案]D[解析]提示: 内心到三边的距离相等10.如图,A 1B 1C 1-ABC 是直三棱柱,∠BCA=90°,点D 1,F 1分别是A 1B 1,A 1C 1的中点,若BC=CA=CC 1,则BD 1与AF 1所成的角的余弦值是[答案]C[解析]取AC 中点E ,连接F 1E ,BE ,三角形F 1EB 中计算即得 二、填空题11.三棱锥ABC P -中,侧棱PC PB PA 、、两两垂直,底面ABC 内一点S 到三个侧面的距离分别是632、、,那么=PS ________. [答案]7[解析]因为侧棱PC PB PA 、、两两垂直,故可以补成一个长方体,以P 点为原点,所以由距离公式即得12.正四棱柱的底面边长为a ,高为)(b a b<,一蚂蚁从顶点A 出发,沿正四棱柱的表面爬到顶点1C ,那么这只蚂蚁所走过的最短路程为_________.[答案 [解析]提示:将正四棱柱的四个侧面展开 13.正三棱锥ABC P -的底面边长为a 2,侧棱a PA =,则二面角C AB P --的大小是______.[答案] 33arccos[解析]取AB 中点E ,连结PE ,CE ,用余弦定理即可14.一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:(1)三角形;(2)菱形;(3)矩形;(4)正方形;(5)正六边形.其中正确的结论是___________________.(把你认为正确的序号都填上) [答案]2,3,4[解析]六边形与六个面均有交线,不可能,三角形则体积不够一半,故均不可以 三、解答题15.如图1,设ABC-A 1B 1C 1是直三棱柱,F 是A 1B 1的中点,且(1)求证:AF ⊥A 1C ; (2)求二面角C-AF-B 的大小.[解析] 先来看第1问,我们“倒过来”分析.如果已经证得AF ⊥A 1C ,则注意到因为AB=2AA 1=2a ,ABC-A 1B 1C 1是直三棱柱,从而若设E 是AB 的中点,就有A 1E ⊥AF ,即AF ⊥平面A 1CE .那么,如果我们能够先证明AF ⊥平面A 1CE ,则就可以证得AF ⊥A 1C ,而这由CE ⊥平面AA 1B 1B 立得.再来看第2问.为计算二面角C-AF-B 的大小,我们需要找到二面角C-AF-B 的平面角.由前面的分析知,CE ⊥平面AA 1B 1B ,而AF ⊥A 1E ,所以,若设G 是AF 与A 1E 的中点,则∠CGE 即为二面角C-AF-B 的平面角,再计算△CGE 各边的长度即可求出所求二面角的大小.解:(1)如图2,设E 是AB 的中点,连接CE ,EA 1.由ABC-A 1B 1C 1是直三棱柱,知AA 1⊥平面ABC ,而CE 平面ABC ,所以CE ⊥AA 1,∵AB=2AA 1=2a ,∴AA 1=a ,AA 1⊥AE ,知AA 1FE 是正方形,从而AF ⊥A 1E .而A 1E 是A 1C 在平面AA 1FE 上的射影,故AF ⊥A 1C ;(2)设G 是AB 1与A1E 的中点,连接CG .因为CE ⊥平面AA 1B 1B ,AF ⊥A 1E ,由三垂线定理,CG ⊥AF ,所以∠CGE 就是二面角C-AF-B 的平面角.∵AA 1FE 是正方形,AA 1=a ,∴1122EGEA a ==,∴CG ==, ∴tan ∠CGE=CG EG ===CGE =60,从而二面角C-AF-B 的大小为60.16.如图,直三棱柱ABC-A 1B 1C 1的底面ABC 为等腰直角三角形,∠ACB=900,AC=1,C 点到AB 1的距离为CE=23,D 为AB 的中点. (1)求证:AB 1⊥平面CED ;(2)求异面直线AB 1与CD 之间的距离; (3)求二面角B 1—AC —B 的平面角.[解析] (1)∵D 是AB 中点,△ABC 为等腰直角三角形,∠ABC=900,∴CD ⊥AB 又AA 1⊥平面ABC ,∴CD ⊥AA 1. ∴CD ⊥平面A 1B 1BA ∴CD ⊥AB 1,又CE ⊥AB 1, ∴AB 1⊥平面CDE ;(2)由CD ⊥平面A 1B 1BA ∴CD ⊥DE ∵AB 1⊥平面CDE ∴DE ⊥AB 1,∴DE 是异面直线AB 1与CD 的公垂线段∵CE=23,AC=1 , ∴CD=.22∴21)()(22=-=CD CE DE ; (3)连结B 1C ,易证B 1C ⊥AC ,又BC ⊥AC , ∴∠B 1CB 是二面角B 1—AC —B 的平面角. 在Rt △CEA 中,CE=23,BC=AC=1,∴∠B 1AC=600 17.如图,在三棱锥ABC —S 中,⊥SA 平面ABC ,1==AC AB ,2=SA ,D 为BC 的中点.(1)判断AD 与SB 能否垂直,并说明理由; (2)若三棱锥ABC —S 的体积为63,且BAC ∠为 钝角,求二面角A BC ——S 的平面角的正切值; (3)在(Ⅱ)的条件下,求点A 到平面SBC 的距离.[解析] (1)因为SB 在底面ABC 上的射影AB 与AD 不垂直,否则与AB =AC 且D 为BC 的中点矛盾,所以AD 与SB 不垂直; (2)设θ=∠BAC ,则632121312=θ⨯⨯⨯⨯=sin VABC DA1E B1C1解得 23=θsin ,所以060=θ(舍),0120=θ. ⊥SA 平面ABC ,AB =AC ,D 为BC 的中点 ∴BC SD BC AD ⊥⊥,,则SDA ∠是二面角S —BC —A 的平面角.在SDA Rt ∆中,4==∠ADSASDA tan , 故二面角的正切值为4;(3)由(2)知,⊥BC 平面SDA ,所以平面SBC ⊥平面SDA ,过点A 作AE ⊥SD ,则AE ⊥平面SBC ,于是点A 到平面SBC 的距离为AE, 从而17172=∠=SDA AD AE sin 即A 到平面SBC 的距离为17172. 18.在边长为a 的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的,并且这三个四边形也全等,如图①.若用剩下的部分折成一个无盖的正三棱柱形容器,如图②.则当容器的高为多少时,可使这个容器的容积最大,并求出容积的最大值.[解析] 设容器的高为x .则容器底面正三角形的边长为x a 32-,)32)(32(3434143)320()32(43)(2x a x a x a x x a x x V --⋅⋅⋅=<<-⋅⋅=∴54)3323234(16133a x a x a x =-+-+≤. 当且仅当 .54,183,32343max a V a x x a x ==-=时即.故当容器的高为a 183时,容器的容积最大,其最大容积为.543a。

棱柱、棱锥、棱台的结构特征【知识梳理】1.空间几何体题型一、棱柱的结构特征【例1】下列关于棱柱的说法:(1)所有的面都是平行四边形;(2)每一个面都不会是三角形;(3)两底面平行,并且各侧棱也平行;(4)被平面截成的两部分可以都是棱柱.其中正确说法的序号是________.[解析](1)错误,棱柱的底面不一定是平行四边形;(2)错误,棱柱的底面可以是三角形;(3)正确,由棱柱的定义易知;(4)正确,棱柱可以被平行于底面的平面截成两个棱柱,所以说法正确的序号是(3)(4).[答案](3)(4)【类题通法】有关棱柱的结构特征问题的解题策略(1)紧扣棱柱的结构特征进行有关概念辨析①两个面互相平行;②其余各面是四边形;③相邻两个四边形的公共边互相平行.求解时,首先看是否有两个平行的面作为底面,再看是否满足其他特征.(2)多注意观察一些实物模型和图片便于反例排除.【对点训练】1.下列四个命题中,假命题为()A.棱柱中两个互相平行的平面一定是棱柱的底面B.棱柱的各个侧面都是平行四边形C.棱柱的两底面是全等的多边形D.棱柱的面中,至少有两个面互相平行解析:选A A错,正六棱柱的两个相对的侧面互相平行,但不是棱柱的底面,B、C、D 是正确的.题型二、棱锥、棱台的结构特征【例2】下列关于棱锥、棱台的说法:(1)用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;(2)棱台的侧面一定不会是平行四边形;(3)棱锥的侧面只能是三角形;(4)由四个面围成的封闭图形只能是三棱锥;(5)棱锥被平面截成的两部分不可能都是棱锥,其中正确说法的序号是________.[解析](1)错误,若平面不与棱锥底面平行,用这个平面去截棱锥,棱锥底面和截面之间的部分不是棱台;(2)正确,棱台的侧面一定是梯形,而不是平行四边形;(3)正确,由棱锥的定义知棱锥的侧面只能是三角形;(4)正确,由四个面围成的封闭图形只能是三棱锥;(5)错误,如图所示四棱锥被平面截成的两部分都是棱锥.[答案](2)(3)(4)【类题通法】判断棱锥、棱台形状的两个方法(1)举反例法:结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.(2)直接法:2.试判断下列说法正确与否:①由六个面围成的封闭图形只能是五棱锥;②两个底面平行且相似,其余各面都是梯形的多面体是棱台.解:①不正确,由六个面围成的封闭图形有可能是四棱柱;②不正确,两个底面平行且相似,其余各面都是梯形的多面体.侧棱不一定相交于一点,所以不一定是棱台.题型三、多面体的平面展开图【例3】如图是三个几何体的侧面展开图,请问各是什么几何体?[解]由几何体的侧面展开图的特点,结合棱柱,棱锥,棱台的定义,可把侧面展开图还原为原几何体,如图所示:所以①为五棱柱,②为五棱锥,③为三棱台.【类题通法】1.解答此类问题要结合多面体的结构特征发挥空间想象能力和动手能力.2.若给出多面体画其展开图时,常常给多面体的顶点标上字母,先把多面体的底面画出来,然后依次画出各侧面.3.若是给出表面展开图,则可把上述程序逆推.【对点训练】3.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图(图中数字写在正方体的外表面上),若图中“0”上方的“2”在正方体的上面,则这个正方体的下面是()A.1B.2C.快D.乐解析:选B由题意,将正方体的展开图还原成正方体,1与乐相对,2与2相对,0与快相对,所以下面是2.【练习反馈】1.下列几何体中棱柱有()A.5个B.4个C.3个D.2个解析:选D由棱柱定义知,①③为棱柱.2.下列图形经过折叠可以围成一个棱柱的是()解析:选D A、B、C中底面边数与侧面个数不一致,故不能围成棱柱.3.棱锥最少有________个面.答案:44.下列几何体中,________是棱柱,________是棱锥,________是棱台(仅填相应序号).答案:①③④⑥⑤5.(1)三棱锥、四棱锥、十五棱锥分别有多少条棱?多少个面?(2)有没有一个多棱锥,其棱数是2 012?若有,求出有多少个面;若没有,说明理由.解:(1)三棱锥有6条棱、4个面;四棱锥有8条棱、5个面;十五棱锥有30条棱、16个面.(2)设n棱锥的棱数是2 012,则2n=2012,所以n=1 006,1 006棱锥的棱数是2 012,它有1 007个面.。
五、 棱锥、棱柱.1. 棱柱.⑴①直棱柱侧面积: (为底面周长, 是高)该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积: (是斜棱柱直截面周长, 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.⑵{四棱柱}{平行六面体}{直平行六面体}{长方体}{正四棱柱}{正方体}. {直四棱柱}{平行六面体}= {直平行六面体}.⑶棱柱具有的性质:①棱柱的各个侧面都是平行四边形, 所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全等的矩形...... ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.注: ①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×)(直棱柱不能保证底面是钜形可如图)②(直棱柱定义)棱柱有一条侧棱和底面垂直.⑷平行六面体:定理一: 平行六面体的对角线交于一点............., 并且在交点处互相平分. [注]: 四棱柱的对角线不一定相交于一点.定理二: 长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.推论一: 长方体一条对角线与同一个顶点的三条棱所成的角为, 则.推论二: 长方体一条对角线与同一个顶点的三各侧面所成的角为, 则.[注]: ①有两个侧面是矩形的棱柱是直棱柱. (×)(斜四面体的两个平行的平面可以为矩形)②各侧面都是正方形的棱柱一定是正棱柱. (×)(应是各侧面都是正方形的直.棱柱才行) ③对角面都是全等的矩形的直四棱柱一定是长方体. (×)(只能推出对角线相等, 推不出底面为矩形)④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交, 可能不相交, 若两条边相交, 则应是充要条件)2. 棱锥: 棱锥是一个面为多边形, 其余各面是有一个公共顶点的三角形.[注]: ①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以.⑴①正棱锥定义: 底面是正多边形;顶点在底面的射影为底面的中心.[注]: i. 正四棱锥的各个侧面都是全等的等腰三角形. (不是等边三角形)ii. 正四面体是各棱相等, 而正三棱锥是底面为正△侧棱与底棱不一定相等Ch S =C h l C S 1=1C l ⊃⊃⊃⊃⊃⋂γβα,,1cos cos cos 222=++γβαγβα,,2cos cos cos 222=++γβα棱柱棱柱3V S h V ==iii. 正棱锥定义的推论: 若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形.②正棱锥的侧面积: (底面周长为, 斜高为) ③棱锥的侧面积与底面积的射影公式: (侧面与底面成的二面角为) 附: 以知⊥, , 为二面角.则①, ②, ③ ①②③得.注: S 为任意多边形的面积(可分别多个三角形的方法).⑵棱锥具有的性质:①正棱锥各侧棱相等, 各侧面都是全等的等腰三角形, 各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形, 正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置: ①棱锥的侧棱长均相等, 则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等, 则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等, 则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等, 则顶点在底面上的射影为底面多边形内心. ⑤三棱锥有两组对棱垂直, 则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直, 则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球, 球心0是各条棱的中垂面的交点, 此点到各顶点的距离等于球半径;⑧每个四面体都有内切球, 球心是四面体各个二面角的平分面的交点, 到各面的距离等于半径.[注]: i. 各个侧面都是等腰三角形, 且底面是正方形的棱锥是正四棱锥. (×)(各个侧面的等腰三角形不知是否全等) ii. 若一个三角锥, 两条对角线互相垂直, 简证: A B ⊥CD , AC ⊥BD BC ⊥AD. 令得, 已知则. iii. 空间四边形OABC 且四边长相等, 则顺次连结各边的中点的四边形一定是矩形.iv. 若是四边长与对角线分别相等, 则顺次连结各边的中点的四边是一定是正方形. 简证: 取AC 中点, 则平面90°'Ch 21S =C 'h αcos 底侧S S =αc l b a =⋅αcos αb l a --l a S ⋅=211b l S ⋅=212b a =⋅αcos ⇒αcos 底侧S S =I ⇒===,,-=⋅⇒=-=-=,()(0,0=-⋅=-⋅c a b b c a 0=-⇒c b c a 0=⋅AD BC 'O ⊥⇒⊥'⊥'AC AC O B AC o o ,=∠⇒⊥⇒'FGH BO AC B O O l ab c B C F E HG B C D A O'易知EFGH 为平行四边形EFGH 为长方形. 若对角线等, 则为正方形.3. 球: ⑴球的截面是一个圆面.①球的表面积公式: .②球的体积公式: . ⑵纬度、经度:①纬度: 地球上一点的纬度是指经过点的球半径与赤道面所成的角的度数.②经度: 地球上两点的经度差, 是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数, 特别地, 当经过点的经线是本初子午线时, 这个二面角的度数就是点的经度.附: ①圆柱体积: (为半径, 为高)②圆锥体积: (为半径, 为高) ③锥形体积: (为底面积, 为高)4. ①内切球: 当四面体为正四面体时, 设边长为a , , , 得. 注: 球内切于四面体: ②外接球: 球外接于正四面体, 可如图建立关系式.⇒EFGH FG EF ⇒=24R S π=334R V π=P P B A ,A B h r V 2π=r h h r V 231π=r h Sh V 31=S h a h 36=243a S =底243a S =侧a a a R R a R a a a 46342334/424331433643222=⋅==⇒⋅⋅+⋅=⋅h S R S 313R S 31V 底底侧ACD B ⋅=⋅+⋅⋅⋅=-O r OR。
棱柱 棱锥知识精要1.多面体的概念:由若干个多边形围成的空间图形叫多面体;每个多边形叫多面体的面,两个面的公共边叫多面体的棱,棱和棱的公共点叫多面体的顶点,连结不在同一面上的两个顶点的线段叫多面体的对角线.2.凸多面体:把多面体的任一个面展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫凸多面体.如图的多面体则不是凸多面体.3.凸多面体的分类:多面体至少有四个面,按照它的面数分别叫四面体、五面体、六面体等4.棱柱的概念:有两个面互相平行,其余每相邻两个面的交线互相平行,这样的多面体叫棱柱底面(简称底);其余各面叫棱柱的侧面;两侧面的公共边叫棱柱的侧棱;两底面所在平面的公垂线段叫棱柱的高(公垂线段长也简称高)5.棱柱的分类:侧棱不垂直于底面的棱柱叫斜棱柱侧棱垂直于底面的棱柱叫直棱柱 底面的是正多边形的直棱柱叫正棱柱棱柱的底面可以是三角形、四边形、五边形……这样的棱柱分别叫三棱柱、四棱柱、五棱柱…… 6.棱柱的性质:(1)棱柱的侧棱相等,侧面都是平行四边形;直棱柱侧面都是矩形;正棱柱侧面都是全等的矩形;(2)棱柱的两个底面与平行于底面的截面是对应边互相平行的全等的多边形; (3)过棱柱不相邻的两条侧棱的截面都是平行四边形7.平行六面体、长方体、正方体:底面是平行四边形的四棱柱是平行六面体.侧棱与底面垂直的平行六面体叫直平行六面体,底面是矩形的直平行六面体长方体,棱长都相等的长方体叫正方体.8.平行六面体、长方体的性质:(1)平行六面体的对角线交于一点,对角线,,,AC BD CA DB ''''相交于一点,且在点O 处互相平分.(2)长方体的一条对角线长的平方等于一个顶点上的三条棱长的平方和9.棱锥的概念:有一个面是多边形,其余各面是有一个公共顶点的三角形,这样的多面体叫棱锥其中有公共顶点的三角形叫棱锥的侧面;多边形叫棱锥的底面或底;各侧面的公共顶点()S ,叫棱锥的顶点,顶点到底面所在平面的垂线段()SO ,叫棱锥的高(垂线段的长也简称高).10.棱锥的表示:棱锥用顶点和底面各顶点的字母,或用顶点和 底面一条对角线端点的字母来表示如图棱锥可表示为S ABCDE -,或S AC -. 11.棱锥的分类:(按底面多边形的边数)分别称底面是三角形,四边形,五边形……的棱锥为三棱锥,四棱锥, 五棱锥……(如图)12.棱锥的性质:如果棱锥被平行于底面的平面所截,那么所得的截面与 底面相似,截面面积与底面面积比等于顶点到截面的距离与棱锥高的 平方比.中截面:经过棱锥高的中点且平行于底面的截面,叫棱锥的中截面13.正棱锥:底面是正多边形,顶点在底面上的射影是底面的中心的棱锥叫正棱锥.(1)正棱锥的各侧棱相等,各侧面是全等的等腰三角形,各等腰三角形底边上的高相等(叫正棱锥的斜高).(2)正棱锥的高、斜高、斜高在底面上的射影组成一个直角三角形;正棱锥的高、侧棱、侧棱在底面上的射影也组成一个直角三角形14.正多面体:每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体. 15.正多面体是一种特殊的凸多面体,它有两个特点:①每个面都是有相同边数的正多边形;②每个顶点处都有相同数目的棱.正多面体的各个面是全等的正多边形,各条棱是相等的线段.16.正多面体共有五种:正四面体、正六面体、正八面体、正十二面体、正二十面体.以上五种正多面体的表面展开图如下:17.棱柱的侧面积是指所有侧面面积之和:S c h =⋅直棱柱(c 为底面周长,h 是高,即直棱柱的侧棱长)S =⨯斜棱柱侧棱长直截面的周长18.棱柱的体积: V S h =⋅热身练习:1. 设M ={正四棱柱},N ={直四棱柱},P ={长方体},Q ={直平行六面体},则四个集合的关系为 ( ). A.MPNQB.MPQNC.PMNQD.PMQN解析:理清各概念的内涵及包含关系. 答案:B2. 如图,在斜三棱柱ABC —A 1B 1C 1中,∠BAC =90°,BC 1⊥AC ,则C 1在底面ABC 上的射影H 必在 ( ).A ABC 11A.直线AB 上B.直线BC 上C.直线AC 上D.△ABC 内部 解析:由AC ⊥AB ,AC ⊥BC 1,知AC ⊥面ABC 1,从而面ABC 1⊥面ABC ,因此,C 1在底面ABC 上的射影H 必在两面的交线AB 上. 答案:A3. 棱柱成为直棱柱的一个必要而不充分条件是 ( ).(A )它的一条侧棱垂直于底面 (B )它的一条侧棱与底面两条边垂直 (C )它的一个侧面与底面都是矩形 (D )它的一个侧面与底面的一条边垂直 4. 一个长方体的全面积是22,体积为8,则这样的长方体 ( ). (A )有一个 (B )有两个 (C )有无数多个 (D )不存在5. 已知正四面体ABCD 的表面积为S ,其四个面的中心分别为E 、F 、G 、H .设四面体EFGH 的表面积为T ,则ST等于 ( ). A.91 B. 94 C. 41 D. 31 解析:如图所示,正四面体ABCD 四个面的中心分别为E 、F 、G 、H ,∴四面体EFGH 也是正四面体. 连结AE 并延长与CD 交于点M , 连结AG 并延长与BC 交于点N . ∵E 、G 分别为面的中心,∴AM AE =AN AG =32.∴MN GE =32. 又∵MN =21BD ,∴BD GE =31.∵面积比是相似比的平方,∴S T =91.答案:A 6.已知长方体ABCD A B C D ''''-中,棱5AA '=,12AB =,那么直线B C ''和平面A BCD ''的距离是 .13607.三棱柱111ABC A B C -,侧棱1BB 在下底面上的射影平行于AC ,如果侧棱1BB 与底面所成的角为030,160B BC ∠=,则ACB ∠的余弦为 .33 8. 将边长为a 的正方形ABCD 沿对角线AC 折起,使BD =a ,则三棱锥D —ABC 的体积为_______122 a3 9. 在三棱锥S —ABC 中,∠ASB =∠ASC =∠BSC =60°,则侧棱SA 与侧面SBC 所成的角的大小是_____________.答案:arccos33 10. 若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的大小等于_______.(结果用反三角函数值表示)解析:取BC 的中点D ,连结SD 、AD ,则SD ⊥BC ,AD ⊥B C.∴∠SDA 为侧面与底面所成二面角的平面角,设为α.在平面SAD 中,作SO ⊥AD 与AD 交于O ,则SO 为棱锥的高. AO =2DO ,∴OD =323.又V S —ABC =31·21AB ·BC ·sin60°·h =1, ∴h =43.∴tan α=DO SO =33243=83.∴α=arctan 83.答案:arctan 8311. 过棱锥高的三等分点作两个平行于底面的截面,它们将棱锥的侧面分成三部分的面积的比(自上而下)为__________.解析:由锥体平行于底面的截面性质知,自上而下三锥体的侧面积之比,S 侧1∶S 侧2∶S 侧3=1∶4∶9,所以锥体被分成三部分的侧面积之比为1∶3∶5.12. 在正四棱柱ABCD —A 1B 1C 1D 1中,E 、F 、G 、H 分别是棱CC 1、C 1D 1、D 1D 、DC 的中点,N 是BC 的中点,点M 在四边形EFGH 的边及其内部运动,则M 只需满足条件__________时,就有MN ⊥AC . 答案:点M 与F 重合说明:本题答案不唯一,当点M 在线段FH 上时均有MN ⊥AC .精解名题例1.已知E 、F 分别是棱长为a 的正方体ABCD —A 1B 1C 1D 1的棱A 1A 、CC 1的中点,求四棱锥C 1—B 1EDF 的体积.AA DBC BCD11111O EH F解法一:连结A 1C 1、B 1D 1交于O 1,过O 1作O 1H ⊥B 1D 于H , ∵EF ∥A 1C 1,∴A 1C 1∥平面B 1EDF .∴C 1到平面B 1EDF 的距离就是A 1C 1到平面B 1EDF 的距离. ∵平面B 1D 1D ⊥平面B 1EDF ,∴O 1H ⊥平面B 1EDF ,即O 1H 为棱锥的高. ∵△B 1O 1H ∽△B 1DD 1, ∴O 1H =D B DD O B 1111⋅=66a ,V EDF B C 11-=31S EDF B 1·O 1H =31·21·EF ·B 1D ·O 1H =31·21·2a ·3a ·66a =61a 3.解法二:连结EF ,设B 1到平面C 1EF 的距离为h 1,D 到平面C 1EF 的距离为h 2,则h 1+h 2=B 1D 1=2a ,∴V EDF B C 11-=V EF C B 11-+V EF C D 1-=31·S EF C 1∆·(h 1+h 2)=61a 3.解法三:V EDF B C 11-=V FD C D E B A 1111-多面体-V 1111D C B A E --V D D C E 11-=61a 3.求体积常见方法有:①直接法(公式法);②分割法;③补形法.例2 如图,正四棱柱1111-D C B A ABCD 中,对角线81=BD ,1BD 与侧面C C BB 11所成角为30,求:(1)1BD 与底面ABCD 所成角;(2)异面直线1BD 与AD 所成角;(3)正四棱柱的全面积.分析:正四棱柱是一种特殊的长方体,它的两底面 ABCD 、1111D C B A 是正方形,长方体中有比较多的线面垂直关系,而线面垂直关系往往是解决立体几何问题的关键条件.题中无论是已知线面成角,还是求线面成角,都要把它们转化为具体的角,落实线面成角,先要找线面垂直关系.异面直线1BD 与AD 所成角通过11//D A AD ,落实为具体的B D A 11∠.正四棱柱各个面都是矩形,求面积只要用矩形面积公式. 解:(1)在正四棱柱C A 1中,∵⊥11C D 面C C BB 11,∴11BC D ∠是B D 1与侧面C C BB 11所成角,即3011=∠BC D . ∵ 81=BD ,∴ 411=C D ,341=BC , ∵ 1111D C B A 是正方形,∴41111==C D C B ,⊥D D 1平面ABCD ,∴ BD D 1∠是B D 1与底面ABCD 所成角,在Rt △DB D 1中,2411==D B BD ,81=BD , ∴22cos 11==∠BD BD BD D ,∴451=∠BD D , 即1BD 与底面ABCD 所成角为45. (2)∵11//D A AD ,∴B D A 11∠是1BD 与AD 所成角(或补角). ∵⊥11A D 平面B B AA 11,∴ B A A D 111⊥,Rt △B D A 11中,411=D A ,81=BD ,∴21cos 11=∠B D A ,∴6011=∠B D A , 即异面直线AD 与1BD 所成角为60.(3)Rt △11C BB 中,411=C B ,341=BC . ∴ 241=BB ,∴ ()()12232244244442+=⨯+⨯+⨯=全S .说明:长方体是一种特殊的棱柱,充分感受其中丰富的线面垂直、线线垂直关系是灵活解题的关键,各种垂直关系是解决立体几何中证明和计算的重要条件.例 3.在三棱锥P ABC -中,ABC ∆为正三角形,90PCA ∠=,D 为PA 中点,二面角P AC B --为120,2,PC AB ==(1)求证:AC BD ⊥;(2)求BD 与底面ABC 所成的角, (3)求三棱锥P ABC -的体积.解:(1)取AC 的E ,连结,BE DE ,则//DE PC ,GE P DCBACBOC 1B 1A 1A由PC AC ⊥,知DE AC ⊥,由ABC ∆为正三角形,得BE AC ⊥, 又DE BE E =,∵AC ⊥平面DEB ,BD ⊂平面DEB ,∴AC BD ⊥. (2)作DG BE ⊥,垂足为G ,∵AC ⊥平面DEB ,DG ⊂平面DEB ,DG AC ⊥,DG ⊥平面ABC ,BD 与底面ABC 所成的角DBG ∠, 由DE AC ⊥,BE AC ⊥知DEB ∠是二面角P AC B --的平面角,120DEB ∠=,∵112DE PC ==,∴2DG =,又∵32BE AB ==, ∴22213213cos12013BD =+-⨯⨯⨯=∴sin 26DG DBE DB ∠==, ∴BD 与底面ABC所成的角为arcsin. (3)∵D 为PA 中点,∴P 到平面ABC的距离2h DG ==,211333P ABC ABC V S h -∆===.例4. 斜三棱柱的底面的边长是4cm 的正三角形,侧棱长为3cm,侧棱1AA 与底面相邻两边都成060角.(1)求证:侧面11CC B B 是矩形; (2)求这个棱柱的侧面积;(3)求棱柱的体积.证明(1):∵1AA 与,AB AC 所成的角都为060,∴A 在面ABC 上的射影O 在CAB ∠的平分线上. 又∵ABC ∆是正三角形 ∴AO BC ⊥ ∴1AA BC ⊥. 又∵11AA BB , ∴1BB BC ⊥, ∴四边形11CC B B 是矩形.(2)解:11021sin 60432AA B B S AB AA =⋅⋅=⨯⨯=,∴112AA C C S =又11214312BB C C S BC CC cm =⋅=⨯=,∴1111112(12AA B B BB C C AA C C S S S S cm =++=+侧. 另法:可以作出直截面11B C H .(3)解:作11OE A B ⊥,垂足为E,连结AE,则11AE A B ⊥. 在1Rt AA E ∆中,0113cos602A E AA =⋅= 在1Rt AOE ∆中,110cos30A EAO == 在1Rt AAO ∆中,AO ==∴11124A B C V S AO ∆=⋅==备选例题例1.(1)多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A 在平面α内,其余顶点在α的同侧,正方体上与顶点A 相邻的三个顶点到α的距离分别为1,2和4,P 是正方体的其余四个顶点中的一个,则P 到平面α的距离可能是:______(写出所有正确结论的编号..) ①3; ②4; ③5; ④6; ⑤7(2)平行四边形的一个顶点A 在平面α内,其余顶点在α的同侧,已知其中有两个顶点到α的距离分别为1和2 ,那么剩下的一个顶点到平面α的距离可能是:①1; ②2; ③3; ④4;以上结论正确的为______________。