关于两类拉伸杆的斜截面应力分布的探究
- 格式:pdf
- 大小:1.75 MB
- 文档页数:2

工程力学第21讲应力状态分析:求斜截面应力在工程力学中,应力状态分析是研究物体受到外力作用后内部应力分布的一门学科。
在实际工程中,经常需要求解物体内部某一点的应力值。
在本文中,我们将着重介绍如何求解斜截面上的应力值。
斜截面应力状态的分析是典型的三维问题,但在一些实际应用中,我们只需要在某一平面上求解应力分量。
为了方便分析,我们通常假设物体是等截面的,其剖面可以看成一个平面截形,如下图所示。
假设物体受到一个外作用力F,我们需要分析该力作用在斜截面xy上,求解点P处的应力状态(包括法向应力σn和切应力τxy)。
点P的坐标可以表示为(x,y,z)。
截面上的任一元素dA的面积可以表示为dA=dxdy,其对应的法向为b。
为了求解点P处的应力状态,我们可以采用以下的步骤:### 第一步:求解对x分量的力和对y分量的力为了便于分析,我们可以将作用力F分解成两个分量F_x和F_y,如下图所示。
在这里,我们需要注意F_x和F_y的方向。
如图所示,F_x沿x轴正方向,F_y沿y轴正方向,因为较难确定夹角a和b的正负号,所以F_x和F_y以及后面的应力分量都是以箭头的方向表示。
同时我们还需要注意到式中的F_z。
如下图所示,我们可以建立一个平面一对应着力分解后的F_x,F_y和截面。
然后我们可以求解在x和y方向上的应力分量。
对应的应力分量为:$$\sigma_x=\frac{F_x}{A_x}$$$$\sigma_y=\frac{F_y}{A_y}$$其中,Ax和Ay分别是上图中标注的x和y方向上的面积。
由于F_x和F_y都垂直于z 轴,所以在z方向上不存在应力分量。
### 第三步:求解点P处的应力状态现在我们已经求解了对x分量的力和对y分量的力在x和y方向上的应力分量,接下来我们需要求解点P处的应力状态。
如下图所示,我们需要确定切线方向上的应力σ_t和法线方向上的应力σ_n。


斜拉实验报告引言:斜拉实验是一种常见的力学实验,用于研究杆件或桥梁的力学性质。
通过施加不同角度的拉力并测量相应的变形,我们可以了解杆件或桥梁在斜拉状态下的强度和稳定性。
本实验旨在通过斜拉实验研究一种新型结构材料的力学性能,并对实验结果进行分析和讨论。
实验方法:首先,我们根据实验要求制备了一根长度为1米、直径为10毫米的实验杆。
然后,我们在实验室灵活调整的支点上悬挂该实验杆,并使用称重仪器施加垂直于实验杆的拉力。
为了保证实验准确性,我们使用多次试验并取平均值。
实验过程:我们首先施加了一个与实验杆呈30度角的斜向拉力,并记录了实验杆的变形情况。
随后,我们逐渐增大拉力,并测量相应的变形。
当拉力达到一定程度时,我们观察到实验杆出现明显的塑性变形,这时我们停止拉力的增加并记录相关数据。
整个实验过程中,我们还注意到了实验室环境因素,如温度和湿度的变化,以排除其对实验结果的影响。
实验结果:通过实验获得的数据,我们制作了一条拉力-位移曲线,并通过曲线上的数据点进行分析。
首先,我们观察到在拉力增加的初期,实验杆的变形较小,与预期一致。
然而,当拉力逐渐增大时,实验杆的变形也随之增加,并且变形速度呈现出逐渐加快的趋势。
最终,当拉力达到杆件的强度极限时,我们观察到杆件出现塑性变形,丧失了原有的结构稳定性。
实验讨论:通过斜拉实验,我们对这种新型结构材料的力学性能有了初步的了解。
首先,我们观察到杆件在不同角度的拉力下会产生不同的变形情况,这说明力的方向对杆件的力学性质有重要影响。
其次,我们观察到杆件在拉力逐渐增大时呈现出塑性变形的特点,这提醒我们在实际工程中选择合适的材料和结构以确保结构的稳定性。
此外,我们还发现在实验过程中环境因素对实验结果有一定影响。
例如,温度的变化可能导致材料的热胀冷缩,从而改变了杆件的刚度和变形特性。
因此,在实际应用中,我们需要考虑环境因素的影响,并进行相应的修正和调整。
结论:通过斜拉实验,我们对一种新型结构材料的力学性能进行了初步研究,并获得了实验结果。



拉压杆横截面上的应力应变及胡克定律机械工业出版社/doc/be3628979.html,用同一材料制成而横截面积不同的两杆,在相同拉力的作用下,随着拉力的增大,横截面小的杆件必然先被拉断。
这说明,杆的强度不仅与轴力的大小有关,而且还与横截面的大小有关,即杆的强度取决于内力在横截面上分布的密集程度。
分布内力在某点处的集度,即为该点处的应力。
第二节拉、压杆横截面上的应力、应变及胡克定理一、杆件在一般情况下应力的概念m F 2F 1O 点F 微内力A 微面积AF p ??=m研究图示杆件。
在截面m-m 上任一点O 的周围取一微小面积?A ,设在?A 上分布内力的合力为?F ,?F 与?A 的比值称为?A 上的平均应力,用p m 表示,即m F 2F 1m F 2F 1O 点?F 微内力A 微面积p m AF p ??=m全应力一般情况下,内力在截面上的分布并非均匀,为了更真实的描述内力的实际分布情况,应使?A 面积缩小并趋近于零,则平均应力p m 的极限值称为m-m 截面上O 点处的全应力,并用p 表示,即OAFA F p A d d lim 0==→?m F P2F P1mF P2F P1K 点F 微内力A 微面积p 全应力K全应力p m 的方向即?F 的方向。
通常将应力分解成垂直于截面的法向分量σ和相切于截面的切向分量τ。
σ称正应力,τ称为切应力。
στ正应力切应力m F P2F P1F P2F P1K 点F 微内力A 微面积p 全应力K在我国的法定计量单位中,应力的单位为Pa(帕),1Pa=1N/m 2。
在工程实际中,这一单位太小,常用兆帕(MPa )和吉帕(GPa ),其关系为1MPa=106Pa ,1GPa=109Pa 。
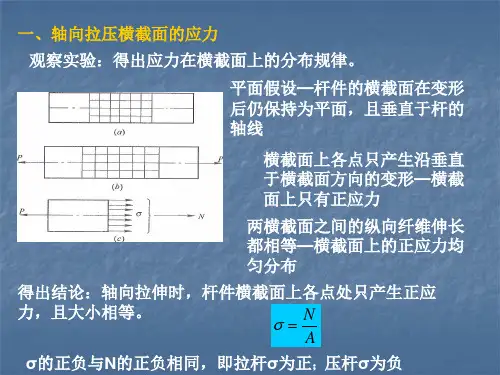
στ正应力切应力/doc/be3628979.html,1.实验观察取一等截面直杆,在杆上画出与杆轴线垂直的横向线1-1和2-2 ,再画上与杆轴向平行的纵向线,然后沿杆的轴线作用拉(压)力F ,使杆件产生拉伸变形。


工程力学中的杆件受力分析和应力分布的分析在工程力学的领域中,杆件受力分析和应力分布的研究是至关重要的。
这不仅关乎到结构的稳定性和安全性,也对工程设计的合理性和经济性有着深远的影响。
杆件,作为常见的工程构件,在各种结构中都发挥着重要作用。
要理解杆件的行为,首先得从受力分析开始。
当杆件受到外力作用时,我们需要明确这些力的大小、方向和作用点。
比如,一个简单的悬臂梁,可能在端部受到垂直向下的集中力,或者在梁的长度方向上受到均匀分布的力。
在进行受力分析时,我们通常会运用力的平衡原理。
这意味着,对于一个处于静止状态的杆件,所有作用在其上的力的合力必须为零,并且对于任何一点,力矩的总和也必须为零。
通过这种方式,我们可以确定未知的力的大小和方向。
以一个水平放置的简支梁为例,假设在梁的中间有一个集中力作用。
我们可以将梁两端的支撑反力分别设为 R1 和 R2 。
根据力的平衡,R1 + R2 等于集中力的大小。
同时,考虑到力矩平衡,以梁的一端为支点,可以得出 R1 和 R2 与集中力和梁的长度之间的关系,从而准确求解出R1 和 R2 的值。
受力分析只是第一步,接下来更关键的是研究应力在杆件中的分布情况。
应力,简单来说,是单位面积上所承受的内力。
它反映了材料内部的受力状态。
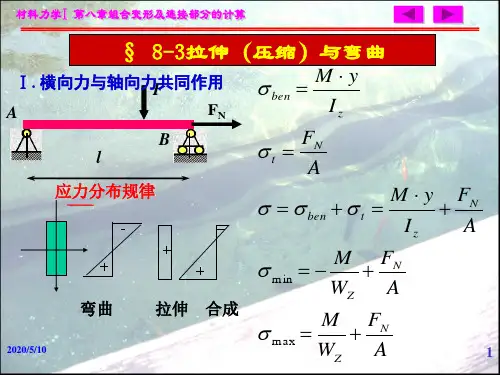
对于拉伸或压缩的杆件,应力在横截面上是均匀分布的。
假设杆件受到一个轴向拉力 F ,横截面积为 A ,那么应力σ 就等于 F / A 。
这种均匀分布的应力对于设计简单的拉杆或压杆非常重要,我们可以根据材料的许用应力来确定杆件所需的横截面积,以保证杆件在工作过程中不会发生破坏。
然而,在实际情况中,杆件的受力往往更加复杂。
比如弯曲的杆件,其应力分布就不再是均匀的。
在弯曲时,杆件的一侧受到拉伸,另一侧受到压缩,而在中性层处应力为零。
应力的大小与到中性层的距离成正比。
为了更准确地描述弯曲应力,我们引入了弯矩的概念。
弯矩越大,弯曲应力也就越大。
而且,杆件的截面形状和尺寸也会影响应力的分布。

斜杆的受力分析
计算斜杆截面内力的基本方法仍然是截面法。
由于斜杆的杆轴与横截面方向都是倾斜的,
因而截面的轴力与剪力方向也是倾斜的.这是斜杆计算中的特点。
直杆内力的微分、增量、积分关系也适用于斜杆,但其中的x 、y 方向过分别换成斜杆轴线的切线、法线方向。
为了说明简支斜杆在竖向荷载作用下的受力特点,比较图2-9a 、b 所示的简支水平梁和指支斜架.二者水平跨度相同,承受的竖向荷载也相同。
由两根梁的整体平行条件可分别计算其支座反力.不难知道,两根梁的支座反力完全相同。
即:
⎪⎭
⎪⎬⎫
====Y Y Y Y X X B 0
B A 0
A A 0
A 0 取隔离体入图2-10a 、b 所示。
若斜梁C 截面上的三个内力分量分别表示为:力偶M C 、水平力X C 和竖向
力Y C ,则可知水平粱内与谢粱内力之间有以下关系:
⎪⎭
⎪
⎬⎫
===M M Q Y X 0
C C 0C C C 0
若将斜粱截面上的竖向力分解为斜粱的剪力Q C 和轴力N C ,便可得到(图2—10c )
⎪⎭
⎪
⎬⎫ϕ-ϕ=SIN COS Q N Q Q 0
C C 0
C C 由此可知,两梁的弯矩彼此相等,斜梁的剪力和轴力分别等于水平梁剪力沿斜梁轴线法向和切向的投影。
例2-2 图2-11a 所示的简支斜梁沿水平线每单位长度内作用竖向荷载q ,求作内力图。
本题,如果将B 支座方向改为与斜杆垂直,那么其弯矩M 图,剪力Q 图都不变,只有轴力N 突发生改变,(B 端为零,A 端为ϕsin ql —-即为一三角形)。
1拉压杆横截面上的应力6.1.1 应力的概念同一种材料制成横截面积不同的两根直杆,在相同轴向拉力的作用下,其杆内的轴力相同。
但随拉力的增大,横截面小的杆必定先被拉断。
这说明单凭轴力F N 并不能判断拉(压)杆的强度,即杆件的强度不仅与内力的大小有关, 图6-1而且还与截面面积有关,即与内力在横截面上分布的密集程度(简称集度)有关,为此引入应力的概念。
要了解受力杆件在截面m-m 上的任意一点C 处的分布内力集度,可假想将杆件在m-m 处截开,在截面上围绕C 点取微小面积ΔA ,ΔA 上分布内力的合力为Δp (图6-1a),将Δp 除以面积ΔA ,即Ap p ∆∆=m (6-1) p m 称为在面积ΔA 上的平均应力,它尚不能精确表示C 点处内力的分布状况。
当面积无限趋近于零时比值Ap ∆∆的极限,才真实地反映任意一点C 处内力的分布状况,即 lim 0dAdp A p p A =∆∆=→∆ (6-2) 上式p 定义为C 点处内力的分布集度,称为该点处的总应力。
其方向一般既不与截面垂直,也不与截面相切。
通常,将它分解成与截面垂直的法向分量和与截面相切的切向分量(图6-1b ),法向分量称为正应力,用σ 表示;切向分量称为切应力,用τ表示。
将总应力用正应力和切应力这两个分量来表达具有明确的物理意义,因为它们和材料的两类破坏现象——拉断和剪切错动——相对应。
因此,今后在强度计算中一般只计算正应力和切应力而不计算总应力。
应力的单位为“帕”,用Pa 表示。
1Pa=1N/m 2, 常用单位为兆帕MPa ,1MPa=106Pa=1MN/mm 2=1N/mm 2,1GPa=109Pa 。
6.1.2 轴向拉伸和压缩时横截面上的正应力取一等截面直杆,在其侧面作两条垂直于杆轴的直线ab 和 cd ,然后在杆两端施加一对轴向拉力F 使杆发生变形,此时直线ab 、 cd分别平移至a 'b '、 c 'd '且仍保持为直线(图6-2a )。