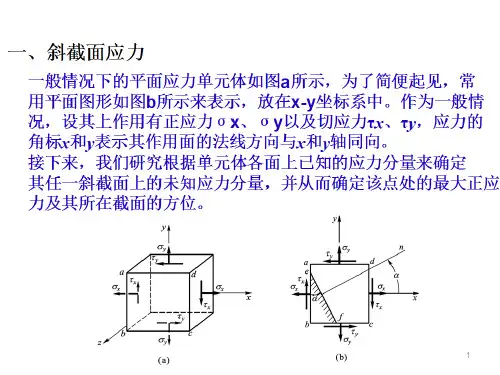
斜截面上的应力

轴向拉伸和压缩时,斜截面上正应力和切应力的公式
轴向拉伸和压缩时，斜截面上正应力和切应力的公式如下：
1. 斜截面上的正应力公式：
σ = σx cos2θ + σy sin2θ
其中，σx 和σy 分别为轴向拉伸和压缩时的正应力，θ为斜截面与轴线的夹角。

2. 斜截面上的切应力公式：
τ = (σx - σy) sin2θ cos2θ
其中，τ为斜截面上的切应力。

需要注意的是，斜截面上的应力分量是相互作用的，也就是说，斜截面上的正应力和切应力是不可分离的。

同时，当θ = 45°时，斜截面上的切应力为零，也就是说，在这种情况下，斜截面上只有正应力。

- 1 -。

材料力学基本知识复习要点1.材料力学的任务材料力学的主要任务就是在满足刚度、强度和稳定性的基础上，以最经济的代价，为构件确定合理的截面形状和尺寸，选择合适的材料，为合理设计构件提供必要的理论基础和计算方法。

2.变形固体及其基本假设连续性假设：认为组成物体的物质密实地充满物体所在的空间，毫无空隙。

均匀性假设：认为物体内各处的力学性能完全相同。

各向同性假设：认为组成物体的材料沿各方向的力学性质完全相同。

小变形假设：认为构件在荷载作用下的变形与构件原始尺寸相比非常小。

3.外力与内力的概念外力：施加在结构上的外部荷载及支座反力。

内力：在外力作用下，构件内部各质点间相互作用力的改变量，即附加相互作用力。

内力成对出现，等值、反向，分别作用在构件的两部分上。

4.应力、正应力与切应力应力：截面上任一点内力的集度。

正应力：垂直于截面的应力分量。

切应力：和截面相切的应力分量。

5.截面法分二留一，内力代替。

可概括为四个字：截、弃、代、平。

即：欲求某点处内力，假想用截面把构件截开为两部分，保留其中一部分，舍弃另一部分，用内力代替弃去部分对保留部分的作用力，并进行受力平衡分析，求出内力。

6.变形与线应变切应变变形：变形固体形状的改变。

线应变：单位长度的伸缩量。

练习题一.单选题1、工程构件要正常安全的工作，必须满足一定的条件。

下列除（）项，其他各项是必须满足的条件。

A、强度条件B、刚度条件C、稳定性条件D、硬度条件2、物体受力作用而发生变形，当外力去掉后又能恢复原来形状和尺寸的性质称为（）A．弹性B．塑性C．刚性D．稳定性3、结构的超静定次数等于（）。

A．未知力的数目B．未知力数目与独立平衡方程数目的差数C．支座反力的数目D．支座反力数目与独立平衡方程数目的差数4、各向同性假设认为，材料内部各点的（）是相同的。

A.力学性质B.外力C.变形D.位移5、根据小变形条件，可以认为（）A.构件不变形B.结构不变形C.构件仅发生弹性变形D.构件变形远小于其原始尺寸6、构件的强度、刚度和稳定性（）A.只与材料的力学性质有关B.只与构件的形状尺寸有关C.与二者都有关D.与二者都无关7、在下列各工程材料中，（）不可应用各向同性假设。

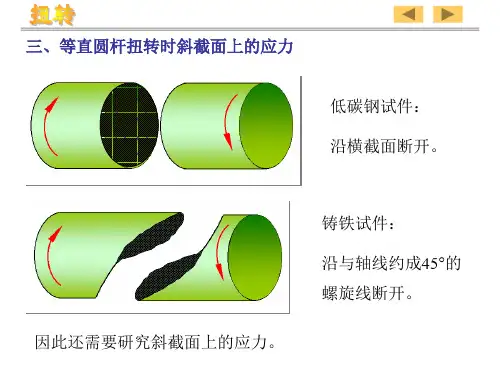
注册土木工程师（港口与航道工程）执业资格考试培训讲稿基础考试：上午4小时120道题每题1分其中材料力学15道题平均每道题用时2分钟。

01年结构考题：拉压2 剪切1 扭转2 截面性质3 弯曲内力2 弯曲正应力3 弯曲变形（含超）2 应力状态强度理论 1 组合变形 2 稳定 102年岩土考题：拉压3 剪切1 扭转2 截面性质2 弯曲内力2 弯曲正应力1 弯曲变形（含超）1 应力状态强度理论 2 组合变形 1 稳定 102年结构考题：拉压3 剪切1 扭转1 截面性质2 弯曲内力2 弯曲正应力2 弯曲变形（含超）1 应力状态强度理论 2 组合变形 1 稳定 2全部是选择题，计算量小根据考试特点复习时应：基本概念要清楚，基本公式和定义要记牢，解题方法要熟练，要培养快速反应能力一、基本概念内力：构件在外力作用下发生变形，引起构件内部各质点之间产生的附加内力（简称内力）。

应力：截面内一点处内力的分布集度。

单位是：N/m2（Pa）、N/mm2（MPa）等。

应力可分为正应力σ和剪应力τ（剪应力）。

位移：构件内任一点由其原来位置到其新位置的连线称为该点的线位移。

构件内某一线段（或平面）由原始位置所转过的角度称为该线段（或平面）的角位移。

变形：构件形状的改变。

应变：构件内任一点处的变形程度。

应变又可分为线应变ε和剪应变γ，均为无量纲量。

线应变ε表示变形前构件内任一点处的一条微线段,变形后的长度改变量与其原始长度之比。

剪应变γ表示过构件内任一点的两个互相垂直的微线段，变形后两个微线段的角度改变量。

例题0 单元体变形后的形状如图中虚线所示，则A点的剪应变是( )。

(A) O，2γ，２γ (B) γ，γ，２γ(C) γ，２γ，２γ (D) O，γ，２γ例题0图答案：D二、四种基本变形的内力、应力及强度、变形1、内力拉压内力：轴力N扭转内力M T弯曲内力Q、M关键点内力的正负号，内力图的画法重点弯曲内力（因拉压、扭转内力较简单）熟练利用剪力、弯矩与分布力的微分关系及其图形的规律判断内力图的正确性。

应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。

绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。

b = 60 mm ，h = 100 mm 。

解题分析：从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。

则各点处的应力状态如图示。

2、梁截面惯性矩为点微体上既有正应力又有切应力。

解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z 1点处弯曲正应力（压应力）MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态，所以021==σσ，MPa 1003−=σ2点为纯剪切应力状态，MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。

平面应力状态公式推导一、平面应力状态的概念。

在物体内一点处的应力状态，如果所有应力作用面都平行于某一平面（设为xy平面），则称该点处于平面应力状态。

此时，在该点处垂直于xy平面方向（设为z方向）上的正应力σ_z和剪应力τ_zx、τ_zy都为零。

（一）单元体表示。

在平面应力状态下，通常取一个微小的正六面体（单元体）来研究该点的应力情况。

单元体的六个面中，有一对面垂直于z轴，由于σ_z = 0，τ_zx=τ_zy = 0，我们主要关注平行于xy平面的四个面上的应力。

设单元体上作用有σ_x、σ_y和τ_xy（τ_yx与τ_xy大小相等），其中σ_x是x面上（外法线沿x轴方向的面）的正应力，σ_y是y面上（外法线沿y轴方向的面）的正应力，τ_xy是x面上沿y方向的剪应力。

二、斜截面应力公式推导。

设斜截面外法线n与x轴正向夹角为α（逆时针方向为正）。

（一）利用平衡条件推导。

1. 建立坐标系和力的分解。

- 取斜截面面积为dA，则x面的面积为dAcosα，y面的面积为dAsinα。

- 根据应力的定义，作用在x面上的力为σ_xdAcosα和τ_xydAcosα（沿x、y 方向分解）；作用在y面上的力为σ_ydAsinα和τ_yxdAsinα（沿x、y方向分解）。

2. 沿斜截面外法线n方向的力平衡。

- 斜截面上的正应力σ_α，根据力的平衡条件∑ F_n=0，有：- σ_αdA=σ_xdAcos^2α+σ_ydAsin^2α + 2τ_xydAsinαcosα- 两边同时除以dA，得到σ_α=σ_xcos^2α+σ_ysin^2α+ 2τ_xysinαcosα- 利用三角函数的二倍角公式cos^2α=(1 +cos2α)/(2)，sin^2α=(1-co s2α)/(2)以及sin2α = 2sinαcosα，可将上式化为：- σ_α=frac{σ_x+σ_y}{2}+frac{σ_x-σ_y}{2}cos2α+τ_xysin2α3. 沿斜截面切线方向的力平衡。