小升初数学课程：第一讲 数与式的认识

第一章 数与数字数学是一门使人精确的学问，而我们从接触数学的第一天起就是“认识数字”，接着就是学习“数与数的关系”。

在我们不断的学习过程中，“数”的范围也在不断的扩大。

我们已经学习了自然数、整数、小数、分数，今后我们还会学习更为复杂的“数”，下面就我们学习的数进行复习。

第一节 数的认识1．请你回忆一下，我们已经学习了哪些“数的概念”？ 1）整数、分数、小数……2）加数、减数、乘数、除数、积、商、余数…… 3）整除、约分、通分…… 4）除法、加法、乘法……2．请你回忆一下，我们知道哪些“运算规则”？1）先乘除，后加减； 2）结合率； 3）交换率； 4）分配率 3．你知道哪些特别数字，它们的特点是什么？ 0： 1： 2：第二节 数的简单运算一、口算下列各题：12+21= 95－59= 45+54= 65－56= 4×6= 2×9= 81÷9= 5×4= 9.3+1.7= 0.56+4.64= 8÷0.08= 100×0.007=5131+= 6141+= =÷15103 =÷683B 71－17= 7×6= 21÷7= 7.33+2.77= 4.24+2.76= 0.4÷200= 3.2×0.125= 7.4－4.7=41－81= 8381+= =⨯8383 912921÷=二、竖式计算并验算：A43+57－12= 61－49－32= 94－66+32=4.53+2.79= 34.5-2.76=5.64+2.6=1.11+9.99=2.53+2.57= 7.84+4.29=B104×16= 124×28= 222×107=30.132÷2.79= 34.5×2.76= 106.652÷2.6=742÷14= 39×275= 1.11×9.99= 三、脱式计算：A5.43+（5.77+0.49）－6.51 （3.48+5.77－7. 43）+6.5+0.243.54+7.61+0.98－（6.22－3.7） 5.98－0.33+4.56－（9.37+0.46）4.76+[0.637－(2.326－2.227)] 7.35－（4.21+0.33）－2.444.25+0.354+4.436－7.475 0.346+[7.56－（6.53－1.344）]B5.43×（5.77+0.49）－6.51 （3.48+5.77×7. 43）×6+0.244.6×[0.637－（2.326－2.227）] 7.35－（4.21+0.33）×2.448.293－（29.221－2.432）÷6.23 8.92÷0.4－3.323－8.7454.25+0.354×4.436－3.475 0.346+7. 6×（6.53－4.344）C6.15115-- %2577.0383-++ 2574722.6-++43)32511(34+-- %)75653(413-+ 2.1)5434(2.3++-)4332511(5.1+-- %)3575.0(54271--+ )]5645(34[2.3---D43)32511(5.1⨯-- %)3575.0(54271-÷+)]5645(2134[212.3-⨯-⨯-%)]302.1(41[259-÷⨯-%)]451(6.1[5124311-÷⨯- )]411%451(6.1[81718-÷⨯÷-第三节 巧算之凑整法一、典型例题1、125×4×25 25×8×125×7×4 123456×52、 56×32＋28×38 84×12＋84×883、11.8×43-860×0.09 34×56＋17×32＋34×284、9999×2222＋3333×3334 1999×1998－1997×19965、9＋99＋999＋9999＋99999 9-0.9-0.09-0.009-0.0009二、巩固练习1、计算下面各题：1994+997×997 10476＋748＋524＋2527.5×27＋19×2.5 1995＋199.5+19.95+1.99576×125×68 1999＋999×9992、计算41.2×8.1＋11×1.25＋537×0.193、计算19971997×1996－19961996×19974、计算3×999＋3＋99×8＋8＋2×9＋2＋95、计算1988×198219821982－1982×198819881988第四节巧算之循环法一、典型例题1、计算1+2+3+……+100 1+3+5+……+992、计算(2008＋2006＋…＋6＋4＋2)－(1＋3＋5＋…＋2005＋2007)3、计算：1000＋999－998－997＋996＋995－994＋993＋…＋104＋103－102－101二、巩固练习1、计算2+4+6+……+100 1+4+7+……+1002、计算（1＋3＋5＋...＋2007）－（2＋4＋6＋ (2006)3、计算（30+28+26+……+4+2）－（29+27+25……＋3+1）4、计算1－2＋3－4＋5－6＋…＋1991－1992＋19935、计算（2003+2001+1999+……+3+1）-（2004＋2002+2000+……+4+2）第五节 巧算之裂项法一、典型例题1、计算4213012011216121+++++ 2、计算：200620051198819871198719861198619851⨯++⨯+⨯+⨯3、计算：100 (3211).....321121111+++++++++++4、计算76516541543143213211⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯二、巩固练习1、计算801631481351241++++2、计算：3、计算：9117816615514513612812111511016131+++++++++++4、计算：90197218561742163015201412136121++++++++ 5、计算2019181715432143211⨯⨯⨯++⨯⨯⨯+⨯⨯⨯第二章 定义新运算一、例题解析1.定义新运算“*”，对于任何数a 和b ，a*b=a b a +；当a=2，b=3时，2*3=232+=2.5 （1）计算1996*1998，1998*1996； （2）计算1997*7*1，1997*（7*1）；2.定义一种运算“∧”，对于任何两个正数a 和b ，a ∧b=ba ab+；计算，2∧4∧8∧16∧16，计算，16∧2∧8∧16∧4。

数与式知识点归纳总结小学数与式是小学数学的重要内容，它涉及到数的认识、运算和运算法则等方面。

下面是对数与式知识点的归纳总结。

一、数的认识与运算1. 自然数：自然数是人们最早认识到的数，包括0和比0大的正整数。

在学习自然数时，需要掌握自然数的读法、书写等基本知识。

2. 整数：整数包括自然数、0和负整数。

在学习整数时，需要掌握整数的顺序关系、相反数等基本概念，以及整数的加减运算法则。

3. 分数：分数是整数的扩展，它表示一个数被等分成若干份中的一份。

在学习分数时，需要理解分数的基本概念，掌握分数的读法、书写和比较大小等方法。

4. 小数：小数是分数的另一种表示形式，它把一个数分成若干部分，其中一部分是整数，另一部分是小数部分。

在学习小数时，需要了解小数的基本概念，掌握小数的读法、书写和四则运算等方法。

5. 有理数：有理数包括整数、分数和小数。

在学习有理数时，需要掌握有理数的基本概念，理解有理数的大小关系，以及有理数的加减乘除运算等规则。

6. 数的运算：数的运算包括加法、减法、乘法和除法。

在进行数的运算时，需要熟练掌握运算法则，理解运算的意义，培养灵活运算的能力。

二、式的认识与运算1. 式的概念：式是由数和运算符号组成的，它表示数与数之间的关系。

在学习式时，需要了解式的构成要素和基本性质，掌握式的读法和书写格式。

2. 代数式：代数式是含有字母的式子，它表示数与未知数之间的关系。

在学习代数式时，需要理解字母的含义，掌握代数式的展开和化简等基本方法。

3. 算式：算式是由数和运算符号组成的式子，它表示数的运算。

在学习算式时，需要掌握算式的读法和书写格式，理解算式的运算过程和结果。

4. 等式：等式是指相等关系的式子，它由等号连接两个算式或代数式。

在学习等式时，需要理解等式的基本性质，熟练掌握等式的变形和解方程的方法。

5. 不等式：不等式是指不相等关系的式子，它由大于号或小于号连接两个算式或代数式。

在学习不等式时，需要掌握不等式的读法和书写格式，理解不等式的基本性质，解不等式的方法。

第一部分：数的认识考点透视：一、整数：整数的计数单位、整数的数位和位数、整数的读法和写法、整数的改写和近似数、 整数的大小比较、整除、公因数和公倍数、质数和合数、奇数和偶数、负数的读写法等。

二、小数：小数的意义、小数的数位和计数单位、小数的读法和写法、小数的性质、小数点移 动引起小数大小的变化、小数的分类、循环小数和不循环小数。

三、分数：分数的意义、分数的分类、分数的读法和写法、分数与除法的关系、分数的基本性 质、分数的大小比较等。

四、百分数：百分数的意义、百分数的读法和写法、成数、折扣、税率、利率等。

典型例题例1：根据信息产业部资料，截止2008年1月，我国手机用户总数达555769000户，横线上的 数读作（ ），它是一个（ ）位数,把它改写成用“万”作单 位的数是（ ），若以“亿”为单位，把它保留两位小数是（ ）。

例2：一个三位数保留一位小数后是3.8，这个三位小数最大的是（ ），最小是（ ）。

例3：填空。

（1）把一条长3米的绳子平均分成5份，每份占这条绳子的（ ），每份是（ ）米。

（2）531的分数单位是（ ），它再增加（ ）个这样的单位就等于最小的质数。

（3）分数单位是81的所有最简真分数的和是（ ）。

例4：把74，57.1%，∙157.0，∙∙175.0四个数按从小到大的顺序排列。

例5：()()8.0%25:)(12====÷）（）（例6：有一个分数，分子加上1可约简为41，分母减去1可以约简为51，则这个分数是 几分之几？基础达标一、填空。

1、2008年北京奥运会我国总计收入人民币12187500000元，这个数读作 （ ）元，把它改写成用“万元”作单位的数是（ ）万元，省略亿后面的尾数约是 （ ）亿元。

2、一个数由五个亿，三十九个万，七十四个百组成，这个数写作（ ），省略万后 面的尾数约是（ ）。

3、一个三位数是由最小的自然数、最小的质数和最小的合数组成的，这个三位数 最小是 （ ），最大是（ ）。

数与式知识点总结一、基本概念1. 数的分类数的分类主要包括自然数、整数、有理数、无理数和实数等。

自然数是最简单的数，包括0、1、2、3……即正整数和零。

整数包括正整数、负整数和零。

有理数是可以写成分数形式的数，无理数则不能用分数形式表示。

实数包括有理数和无理数。

2. 数轴及数的比较数轴是用来表示数的一条直线，通过数轴可以方便地对数进行比较。

在数轴上，数越往右越大，越往左越小，可以通过数轴方便地表示数的大小关系。

3. 数的运算数的运算包括加法、减法、乘法和除法。

加法和乘法满足交换律和结合律，减法和除法则不满足。

另外，零是加法和乘法的零元素，1是乘法的幺元素。

二、式的概念1. 代数式代数式是由常数、变量、运算符号和括号等符号组成的表达式，可以表示数或者表示一种计算关系。

代数式由于有变量的存在，所以具有一定的未知数的性质。

2. 方程与不等式方程是含有未知数的等式，可以通过求解来得到未知数的值。

不等式则是关于未知数的大小关系的式子，可以表示一种范围。

三、数与式的运算1. 加减法数的加减法是最基本的运算，可以通过列竖式进行计算。

代数式的加减法也是基本的运算操作，需要根据运算法则进行化简和计算。

2. 乘除法乘法和除法是数学中重要的运算，也是代数式合并、化简的重要手段。

3. 括号运算括号运算是代数式中优先级最高的运算，可以通过括号对式子进行分解、合并和化简。

4. 有理数的加减乘除运算有理数的加减乘除运算是数学中的重要内容，需要注意正负号的运算规则，以及除法中的零的性质等。

五、方程与不等式1. 一元一次方程一元一次方程是代数中的基础内容，通过解一元一次方程可以得到未知数的值，方程的解就是方程的根。

2. 一元一次不等式一元一次不等式是关于未知数的大小关系的式子，可以通过求解得到不等式的解集。

3. 二元一次方程二元一次方程是含有两个未知数的一次方程，通过解二元一次方程可以得到未知数的值。

4. 二元一次不等式二元一次不等式是含有两个未知数的不等式，通过求解可以得到不等式的解集。

第一章数与式知识点归纳第一章数与式一、数的分类数可以分为正整数、负整数、零、正分数、负分数、正有理数、负有理数、正无理数、负无理数和实数。

其中有理数是可以比较大小的数，可以是有限小数或无限循环小数，而无理数是无限不循环小数。

二、数轴数轴有三个要素：原点、正方向和单位长度。

数轴上的点与实数是一一对应的，利用数轴可以比较数的大小，理解实数的相反数和绝对值等概念。

三、绝对值数a的绝对值表示数轴上表示a的点与原点的距离，可以用几何定义或代数定义来表示。

四、相反数和倒数两个数互为相反数当且仅当它们的和为0，互为倒数当且仅当它们的积为1.在非负数的情况下，平方根和立方根的概念也很重要。

五、非负数的性质几个非负数之和为0时，这几个数也必须为0.同时，非负数的平方大于等于0，非负数的倒数也必须是非负数。

六、幂和算术平方根an表示a的n次幂，其中a为底数，n为指数。

算术平方根和立方根的概念也很重要。

七、运算顺序和律运算顺序包括同级从左到右和不同级从高到低，有括号时要从里到外计算。

运算律包括交换律、结合律和分配律。

八、运算法则加法法则包括两数相加和相减，乘法法则包括两数相乘和相除。

减法可以转化为加法，除法可以转化为乘法。

九、a＞０的性质当a＞0时，(-a)的偶次幂为正，奇次幂为负。

十、有理式有理式是由有理数和变量构成的式子，可以进行加减乘除等运算。

单项式是只有一个变量的代数式，它有一个次数和一个系数。

整式是由多个单项式相加或相减而成的代数式，它有一个最高次数和一个项数。

有理式是整式的分式形式，分式有分子和分母，分母不为零。

多项式是整式的一种，它只有加减运算，没有乘除运算。

乘法公式是代数中常用的公式，包括平方差公式和完全平方公式。

平方差公式是指两个数的平方差等于它们的积，即（a＋b）（a—b）＝a2－b2.完全平方公式是指一个二次多项式可以写成两个一次多项式的平方和，即（a±b）2＝a2±２a b＋b2.分式是有理式的一种，它由分子和分母组成，分母不为零。

数与式知识点总结数与式是数学中重要的基础知识点，它们是关于数字和代数表达式的概念、性质和运算规则。

本文将从数与式的定义、分类、性质和运算规则等方面进行总结，以帮助读者理解和掌握这一知识点。

一、数的概念和性质1.数的定义：数是用来计数或度量的基本概念。

数可以分为自然数、整数、有理数和实数等几类。

2.自然数：自然数是用来计数的数，包括0和正整数，用符号N表示。

3.整数：整数是正整数、0和负整数组成的集合，用符号Z表示。

4.有理数：有理数是可以表示为两个整数之比的数，包括整数和分数，用符号Q表示。

5.实数：实数是可以用小数或无理数表示的数，包括有理数和无理数。

6.数的性质：数具有封闭性、比较性、传递性和稀疏性等性质。

二、式的概念和性质1.式的定义：式是由数和运算符号组成的代数表达式。

式可以分为算术式、代数式和方程等类型。

2.算术式：算术式是由数和四则运算符号组成的表达式，如2+3-4*5/63.代数式：代数式是由数、字母和运算符号组成的表达式，如2x+y-3z。

4.方程：方程是由等号连接的两个代数式构成的等式，如2x+y-3z=7三、数的运算规则1.加法和减法：加法具有交换律和结合律，减法是加法的逆运算。

2.乘法和除法：乘法具有交换律和结合律，除法是乘法的逆运算。

3.混合运算：混合运算时，先乘除后加减，可以使用分配律和结合律。

4.乘方和开方：乘方是数的自乘运算，开方是乘方的逆运算。

5.有理数的运算：有理数的运算可以转化为分数的运算，使用通分、约分和换位律等方法。

四、式的运算规则1.同类项的合并：同类项是指含有相同的字母和相同的次数的项，可以合并为一个项。

2.移项和整理：在代数式中，将含有未知数的项移到等式的同一边，并整理为一般形式。

3.因式分解：将代数式表示为不可再分解为更简单的乘积的形式，称为因式分解。

4.公因式提取：将代数式中的公因式提取出来，有利于后续的因式分解和计算。

5.计算器法则：使用计算器可以进行表达式的计算，包括代数式的运算、方程的求解等。

小学数学重点认识简单的数学代数和方程式数学代数和方程式是小学数学的重点内容之一，它们是数学思维发展的基础，对于培养学生的逻辑思维和解决问题的能力起着至关重要的作用。

本文将从认识数学代数和方程式的基本概念，介绍它们的应用方法以及解决实际问题的实例三个方面进行探讨。

一、数学代数和方程式的基本概念数学代数是研究数学结构和运算规律的分支学科，它通过将数学问题抽象化，用字母来表示数，推导出数学公式和规律，从而解决实际问题。

在小学阶段，学生开始接触代数，理解和掌握数学表达式、变量、常数和运算符等基本概念是非常重要的。

1.1 数学表达式数学表达式是用数、字母、运算符和括号等符号表示的数学语句，它可以进行各种数学运算。

例如，2+3、4x-1、a+b等都是数学表达式。

学生需要学会识别和阅读数学表达式，并理解其含义。

1.2 变量和常数在数学代数中，字母通常表示未知数，称为变量。

变量可以代表任何数。

而数字中已知的数称为常数。

例如，在表达式2x+3中，x是变量，2和3都是常数。

理解并正确使用变量和常数是解决代数问题的关键。

1.3 运算符运算符用于表示数学运算的符号，例如加减乘除等。

学生需要掌握各种运算符的表示方法，并理解其运算规则。

例如，在数学表达式3x+2中，+表示加法运算。

二、数学代数和方程式的应用方法了解数学代数和方程式的基本概念后，学生可以通过应用方法来解决各种数学问题。

下面介绍一些常见的应用方法。

2.1 代数式的化简化简代数式是代数运算的基本要求，它可以使代数式更加简洁。

通过运用运算性质，例如结合律、分配律和交换律等，将代数式中的相同项合并、括号展开和合并同类项等，使表达式更加简洁明了。

2.2 代数方程的解方程是代数中的重要概念，它通过等号将两个代数式连接起来，要求求出未知数的值。

解方程过程中，可以通过移项、合并同类项、消去和分配律等运算方法，逐步推导求解出未知数的值，从而得到方程的解。

2.3 代数式的应用代数式的应用是将代数式与实际问题相结合，通过数学模型解决实际问题。

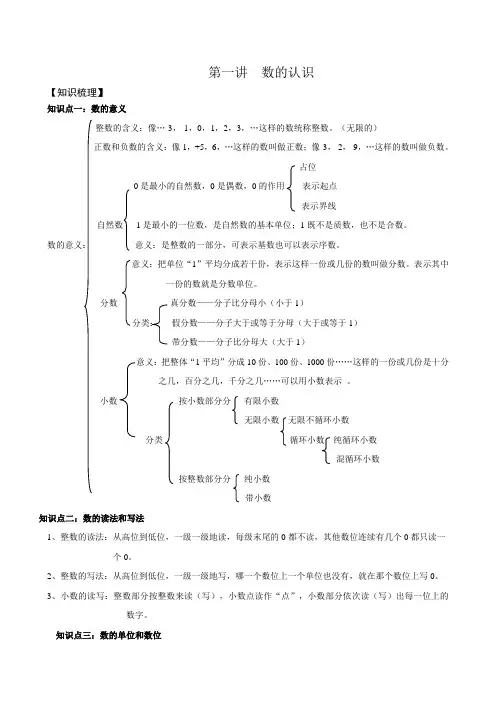
第一讲数的认识【知识梳理】知识点一：数的意义整数的含义：像…-3，-1，0，1，2，3，…这样的数统称整数。

（无限的）正数和负数的含义：像1，+5，6，…这样的数叫做正数；像-3，-2，-9，…这样的数叫做负数。

占位0是最小的自然数，0是偶数，0的作用表示起点表示界线自然数1是最小的一位数，是自然数的基本单位；1既不是质数，也不是合数。

数的意义：意义：是整数的一部分，可表示基数也可以表示序数。

意义：把单位“1”平均分成若干份，表示这样一份或几份的数叫做分数。

表示其中一份的数就是分数单位。

分数真分数——分子比分母小（小于1）分类：假分数——分子大于或等于分母（大于或等于1）带分数——分子比分母大（大于1）意义：把整体“1平均”分成10份、100份、1000份……这样的一份或几份是十分之几，百分之几，千分之几……可以用小数表示。

小数按小数部分分有限小数无限小数无限不循环小数分类循环小数纯循环小数混循环小数按整数部分分纯小数带小数知识点二：数的读法和写法1、整数的读法：从高位到低位，一级一级地读，每级末尾的0都不读，其他数位连续有几个0都只读一个0。

2、整数的写法：从高位到低位，一级一级地写，哪一个数位上一个单位也没有，就在那个数位上写0。

3、小数的读写：整数部分按整数来读（写），小数点读作“点”，小数部分依次读（写）出每一位上的数字。

知识点三：数的单位和数位数位顺序表。

知识点四：数的改写（要注意以“一”为单位）1、多位数的改写和省略：写成用“万”或“亿”作单位的数省略“万”或“亿”位后面的尾数2、分数、小数、百分数的互化改写成分母是10、100、1000…的分数再约分小数分数用分子除以分母小数点向右移动两位，同时添上%小数百分数去掉%，小数点向左移动两位写成分数形式并约分百分数分数先写成小数，再写成百分数3、近似数：四舍五入法（近似数，精确到，保留到）、进一法（坐车）、去尾法（切正方形）。

知识点五：比较大小1、整数的大小比较：先看位数，位数多的数大；位数相同，从高位看起相同数位上的数大的那个数就大。

2016-2017学年高中语文单元综合测评3 新人教版必修1新人教版单元综合测评(三) 第三单元(时间：120分钟，分值：120分)一、根底稳固(12分，每题3分)1．依次填入下面语段横线处的词语，最恰当的一组是( )【：91110110】散文能够真正地见出一位作家的个性和______。

阅读散文，我们能体味到鲁迅的________，冰心的________，梁实秋的幽默机智，丰子恺的清雅淡泊。

“情〞是散文的命脉和灵魂，对于散文的“情〞来说，真挚________。

A．情趣冷峻深沉温和娴雅至关重要B．情趣冷峭阴沉冲淡平和至关重要C．情调冷峭阴沉温和娴雅举足轻重D．情调冷峻深沉冲淡平和举足轻重【解析】此题考查近义词的辨析。

“情趣〞的意思是“性情志趣，情调趣味〞；“情调〞的意思是“思想感情所表现出来的风格，事物所具有的能引起人的各种不同情感的性质〞。

此处的主体是人，应选“情趣〞。

“冷峻深沉〞的意思是“冷酷严峻，沉着而严肃〞；“冷峭阴沉〞形容寒气逼人或态度严峻，话语尖刻。

“温和娴雅〞指态度温和，文雅(多形容女子)；“冲淡平和〞的意思是谦虚、淡泊，心态平和。

“阴沉〞带有贬义色彩，此处应选“冷峻深沉〞，再根据冰心的人品和文品，选择“温和娴雅〞。

“至关重要〞指相当重要，是解决问题时的关键点；“举足轻重〞指处于重要地位，一举一动都足以关系到全局。

前者的语义比后者重，与题干中“命脉和灵魂〞地位相符的只能是“至关重要〞。

【答案】 A2．以下各句中，没有语病的一句是( )【：91110111】A．一切儿童文学作品都应该永远持着守护童年的立场，遵循儿童思维开展规律，富有丰富的想象力，充满爱与希望，传递古老传统中的善与美。

B．在深化改革的关键阶段，我们是否能够保持积极的精神状态，关系到我省经济的长远开展，关系到全省人民的福祉，就必须防止“精神懈怠〞。

C．自从实施飞行员培训方案后，学员报名十分踊跃，有航空爱好者，有想开飞机节省时间的企业家，还有一些家长想给孩子增加一项实用技能。

六年级（下）数学讲义：第1讲总复习：数的认识✍一、考点分析本节我们主要复习数的认识部分。

数的认识：亿以内的数的读、写，负数的意义，十进制计数法；小数、分数、百分数之间的转化及大小的比较；被2、3、5整除的数的特征，求最大公因数和最小公倍数；奇数、偶数、质数、合数的意义和性质。

此专项考点分布广泛，需考生对各类数的知识有全面了解和把握，从十六校联考的历年试题来看，是养生考查基础知识和能力。

二、知识要点 知识结构()()()()()()()()()()()11.212.23123.3,,4514.⎧⎨⎩⎧⎪⎨⎪⎩⎧⎪⎪⎪⎨⎪⎪⎪⎩整数，自然数，小数，分数和百分数的意义数的意义小数，分数的基本性质数位的顺序：整数的数位顺序，小数的数位顺序数的读法和写法数的读法：包括整数，小数，分数和百分数数的写法：包括整数，小数，分数和百分数整除和除尽的意义数的认识因数和倍数数的整除能被235整除的数的特征质数，合数，分解质因数最大公因数与最小公倍数整数的改数的改写()()23⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧⎪⎪⎨⎪⎪⎪⎩⎩写求整数，小数的近似数整数，小数，分数和百分数的互化1、整数、自然数、小数、分数和百分数的意义与性质1）分数和除法的关系：被除数÷除数=被除数除数 (除数不为0)，用字母表示：（ ）。

2）比较分数的大小：当分母相同的两个分数相比，分子大的分数就大。

当分子相同（0除外）的两个分数相比，分母小的分数就大。

3）真分数：分子比分母小的分数。

真分数<1假分数：分子比分母大或者分子和分母相等的分数。

假分数≥1 带分数：整数和真分数合成的分数。

4）百分数的意义：表示一个数是另一个数的百分之几的数，叫做百分数，又叫百分率或百分比。

5）小数、分数的基本性质：小数的基本性质：在小数末尾添上零或去掉零，小数的大小不变。

分数的基本性质：分数的分子和分母都乘以或者除以相同的数（零除外），分数的大小不变。

数与式知识点数学是一门充满魅力和智慧的学科，而数与式则是数学的基础。

数与式的知识贯穿了从小学到高中乃至大学的数学学习过程。

接下来，让我们一起深入了解数与式的重要知识点。

一、数的概念1、自然数自然数是指用以计量事物的件数或表示事物次序的数，即用数码0，1，2，3，4……所表示的数。

自然数由 0 开始，一个接一个，组成一个无穷集体。

2、整数整数包括正整数、零和负整数。

正整数和 0 统称为自然数。

整数的全体构成整数集，整数集是一个数环。

3、分数把单位“1”平均分成若干份，表示这样的一份或几份的数叫分数。

表示其中一份的数，叫作分数单位。

4、小数小数由整数部分、小数部分和小数点组成。

当测量物体时往往会得到的不是整数的数，古人就发明了小数来补充整数。

小数是十进制分数的一种特殊表现形式。

5、有理数有理数为整数（正整数、0、负整数）和分数的统称。

6、无理数无理数，也称为无限不循环小数，不能写作两整数之比。

若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环。

二、数的运算1、加法把两个（或几个）数合并成一个数的运算，叫做加法。

相加的两个数叫做加数，加得的数叫做和。

2、减法已知两个加数的和与其中一个加数，求另一个加数的运算，叫做减法。

在减法中，已知的和叫做被减数，减去的已知加数叫做减数，求出的未知加数叫做差。

3、乘法求几个相同加数的和的简便运算，叫做乘法。

相乘的两个数叫做因数，乘得的数叫做积。

已知两个因数的积与其中一个因数，求另一个因数的运算，叫做除法。

在除法中，已知的积叫做被除数，已知的因数叫做除数，求出的未知因数叫做商。

5、四则混合运算加法、减法、乘法和除法统称四则运算。

在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

在没有括号的算式里，既有乘、除法又有加、减法的，要先算乘除法，再算加减法。

算式有括号，要先算括号里面的，再算括号外面的；大、中、小括号的计算顺序为小→中→大。

明灯教育·小升初数学教案第一章：数的认识1.1 整数的认识学习整数的定义及性质，理解整数的分类（正整数、负整数、零）掌握整数的计数单位，如个、十、百、千等进行整数的加减乘除运算，理解运算规律和运算性质1.2 分数的认识学习分数的定义及性质，理解分数的分类（正分数、负分数）掌握分数的计数单位，如分之一、之二、之分三等进行分数的加减乘除运算，理解运算规律和运算性质第二章：代数式的认识2.1 代数式的基本概念学习代数式的定义及组成，理解代数式的表示方法掌握代数式的运算规则，如加减乘除、乘方等2.2 方程的解法学习方程的定义及解法，理解方程的解的概念掌握一元一次方程、一元二次方程的解法第三章：几何图形的认识3.1 平面图形的认识学习平面图形的定义及性质，理解不同平面图形的特点掌握平面图形的计算方法，如三角形、矩形、圆形等3.2 立体图形的认识学习立体图形的定义及性质，理解不同立体图形的特点掌握立体图形的计算方法，如立方体、圆柱体、球体等第四章：统计与概率4.1 统计的基本概念学习统计的定义及方法，理解数据的收集、整理和表示掌握统计图表的绘制，如条形图、折线图、饼图等4.2 概率的基本概念学习概率的定义及计算方法，理解事件的可能性和必然性掌握简单概率的计算，如抛硬币、抽签等第五章：解决问题的方法5.1 问题解决的基本步骤学习问题解决的方法和步骤，理解分析问题、制定计划、执行计划、检查结果的过程5.2 典型问题类型及解法学习不同类型的问题及解法，如应用题、几何题、概率题等掌握解题技巧和策略，如画图、列方程、列举法等明灯教育·小升初数学教案第六章：数的运算6.1 整数的加减乘除复习整数的加减乘除运算规则，通过具体例子讲解运算顺序和运算性质练习不同难度的整数运算题目，提高运算速度和准确性6.2 分数的加减乘除复习分数的加减乘除运算规则，通过具体例子讲解运算顺序和运算性质练习不同难度的分数运算题目，提高运算速度和准确性第七章：代数式的运用7.1 代数式的四则运算学习代数式的四则运算规则，通过具体例子讲解运算顺序和运算性质练习不同难度的代数式运算题目，提高运算速度和准确性7.2 代数式的应用通过实际问题，学会运用代数式解决问题，培养学生的应用能力练习不同难度的代数式应用题目，提高解决问题的能力第八章：几何图形的运算8.1 平面图形的面积计算复习平面图形的面积计算方法，如三角形、矩形、圆形等练习不同难度的平面图形面积计算题目，提高计算准确性和速度8.2 立体图形的体积计算复习立体图形的体积计算方法，如立方体、圆柱体、球体等练习不同难度的立体图形体积计算题目，提高计算准确性和速度第九章：统计与概率的应用9.1 统计的方法与应用学习统计的方法和步骤，通过实际数据进行数据的收集、整理和表示练习不同难度的统计题目，提高数据分析能力9.2 概率的计算与应用学习概率的计算方法，通过实际问题进行事件的可能性和必然性的分析练习不同难度的概率题目，提高概率计算能力第十章：总复习与测试10.1 复习重点知识点复习整个小升初数学阶段的重要知识点，巩固学生的学习成果通过复习，帮助学生建立知识体系，提高综合运用能力10.2 进行阶段测试安排一次全面的阶段测试，检验学生的学习效果根据测试结果，为学生提供个性化的辅导和建议，帮助其提高学习成绩。

初中数学是每个学生必须学习的重要学科之一。

在初中数学中，数与式是一项基础而又重要的知识点。

本文将通过逐步思考的方式介绍数与式的相关知识点。

1. 数的基本概念在数学中，我们首先要了解数的概念。

数是用来计算和表示数量的工具。

数可以分为自然数、整数、有理数和实数等不同的类型。

自然数指的是从1开始的正整数，例如1、2、3等。

整数包括正整数、负整数和零，例如-3、0、5等。

有理数是可以表示为两个整数的比值，例如1/2、2/3等。

实数则包括有理数和无理数，例如根号2、π等。

2. 数的运算了解了数的概念后，我们需要学习数的运算。

数的运算包括加法、减法、乘法和除法。

加法是将两个数相加的操作，例如 2 + 3 = 5。

减法是将一个数减去另一个数的操作，例如 5 - 3 = 2。

乘法是将两个数相乘的操作，例如 2 × 3 = 6。

除法是将一个数除以另一个数的操作，例如 6 ÷ 2 = 3。

3. 式的概念在数与式的学习中，我们需要了解式的概念。

式是由数和运算符号组成的代数表达式。

在式中，我们可以使用字母来代表未知数，例如 x、y等。

通过代入具体数值，我们可以求解未知数的值。

4. 简单的代数式学习了式的概念后，我们可以开始学习一些简单的代数式。

例如，3x表示3乘以未知数x，2y表示2乘以未知数y。

我们可以对这些代数式进行加法、减法、乘法和除法运算。

例如，3x + 2y表示3x和2y的和。

5. 一元一次方程在代数式的基础上，我们可以进一步学习一元一次方程。

一元一次方程是指只含有一个未知数的一次方程。

例如，2x + 3 = 7就是一个一元一次方程。

我们可以通过移项和合并同类项的方式解方程，求出未知数的值。

6. 二元一次方程除了一元一次方程，我们还可以学习二元一次方程。

二元一次方程是指含有两个未知数的一次方程。

例如，2x + 3y = 7就是一个二元一次方程。

解二元一次方程需要使用联立方程的方法，通过消元或代入的方式求解出两个未知数的值。

小升初数学基本知识基本概念(1) 第一章数和数的运算一概念(一)整数1整数的意义自然数和0都是整数。

2自然数我们在数物体的时候，用来表示物体个数的1，2，3……叫做自然数。

一个物体也没有，用0表示。

0也是自然数。

3计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。

每相邻两个计数单位之间的进率都是10。

这样的计数法叫做十进制计数法。

4数位计数单位按照一定的顺序排列起来，它们所占的位置叫做数位。

5数的整除整数a除以整数b(b≠0)，除得的商是整数而没有余数，我们就说a能被b整除，或者说b能整除a。

如果数a能被数b(b≠0)整除，a就叫做b的倍数，b就叫做a的约数(或a的因数)。

倍数和约数是相互依存的。

因为35能被7整除，所以35是7的倍数，7是35的约数。

一个数的约数的个数是有限的，其中最小的约数是1，最大的约数是它本身。

例如：10的约数有1、2、5、10，其中最小的约数是1，最大的约数是10。

一个数的倍数的个数是无限的，其中最小的倍数是它本身。

3的倍数有：3、6、9、12……其中最小的倍数是3，没有最大的倍数。

个位上是0、2、4、6、8的数，都能被2整除，例如：202、480、304，都能被2整除。

个位上是0或5的数，都能被5整除，例如：5、30、405都能被5整除。

一个数的各位上的数的和能被3整除，这个数就能被3整除，例如：12、108、204都能被3整除。

一个数各位数上的和能被9整除，这个数就能被9整除。

能被3整除的数不一定能被9整除，但是能被9整除的数一定能被3整除。

一个数的末两位数能被4(或25)整除，这个数就能被4(或25)整除。

例如：16、404、1256都能被4整除，50、325、500、1675都能被25整除。

一个数的末三位数能被8(或125)整除，这个数就能被8(或125)整除。

例如：1168、4600、5000、12344都能被8整除，1125、13375、5000都能被125整除。