06曲线测设

7.1.8曲线测设本工程由于功能上的需要，在建筑结构设计上，设计了10条圆弧曲线，圆弧曲线的半径17.400m～59.195m，同时由于本工程为多功能的比赛场馆，在各比赛场馆中，需要在场地上划分出各种半径的圆弧比赛标志线。

曲线测设时首先测设欲设曲线的控制线（设计曲线的等距线），然后依据控制线沿法线方向用小盒尺定出施工所需的墙、柱位置（轴线的等距曲线）。

控制线到设计曲线的距离控制在1m 以内。

曲线上各测点的密度，即相邻两测点的间距应根据施工精度的要求进行确定，相邻两点的矢高要求小于8mm，弹线时将墨线中间向外捻至矢高点，再分两段弹线，将曲线的实际矢高控制在2mm 以内。

圆曲线测设主要采用极坐标法测设，辅以长弦纵距法、四分高法和全站仪坐标放样法，施测时视具体情况采用相应的测法，对于半径小于15m 的圆曲线采用钢尺直接量设的方法。

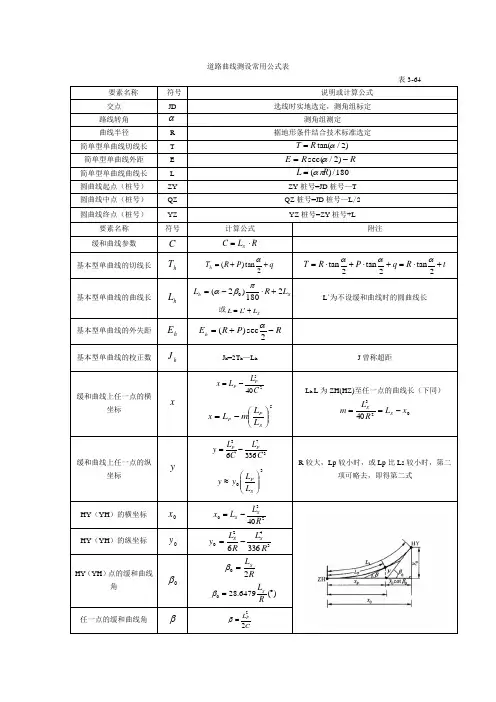
7.1.8.1极坐标法a.特点：极坐标法是建筑施工中圆曲线测设中最常用的方法，它计算简便，所测设的各辅点的误差分配均匀，受系统误差影响小，对施工流水段的适应性强，测设速度快，易于掌握，便于提高工效。

b.适用范围：它适用于R≥15.000m的圆曲线测设，施测面要求基本上水平，具有良好的丈量和通视条件。

适合于在曲线的内侧进行测设。

c.施测原理如上图：极坐标法是根据曲线起点M和曲线上任意点P的弦长和过M点的弦切点来确定P点的位置，通过不断变化弦切角定出曲线上任意点的位置。

d.施测流程：确定曲线的起点M和切线方向T→根据控制条件计算放样数据→向施测面投测控制线→测设圆曲线上各辅助点的位置→将各辅点连接成近似的圆曲线7.1.8.2角度交会法a.特点和适用范围：该方法在测设过程中不用量边，适用于通视条件较好，但施测面地形复杂，量距不便的情况。

b.测设原理根据几何原理，在圆上弦所对应的任意圆周角Ψ相等，其两底角之和等于180º-Ψ，当圆周角已知后，用两台经纬仪同时依次设出两底角，则两条方向线的交点为曲线线辅点的位置。

•线路的空间位置是由它的平面和纵断面决定的•线路平面：线路中心线在水平面上的投影，表示线路平面状况。

•线路纵断面：是沿线路中心线所作的铅垂剖面展直后、线路中心线的立面图，表示线路起伏情况，其高程为路肩高程。

•曲线的测设线形组成•道路由于受自然条件的限制，在平面上有转折，纵面上有起伏。

在转折点和起伏变化点处为满足车辆行驶的顺适、安全和一定速度的要求，必须用一定半径的曲线连结。

•故路线在平面和纵面上都是由直线和曲线两大部分组成。

平面上的曲线称为平曲线，而纵断面则是道路中线在立面上的投影，起伏是指竖向标高的变化，故纵面上的曲线称为竖曲线。

•线路平纵面设计满足三个基本要求：•平竖曲线计算式示意图•一、线路平面组成和平面位置的标志•§4 圆曲线的测设（circular curve location）–铁路线路平面曲线部分为两种类型：一种是圆曲线，主要用于专用线和行车速度不高的线路上；另一钟是带有缓和曲线的圆曲线，铁路干线上均用此种曲线。

•曲线测设一般分两步进行，先测设曲线主点，然后依据主点详细测设曲线。

•曲线测设常用方法：偏角法、切线支距法和极坐标法。

•一、圆曲线要素计算与主点测设•为了测设圆曲线的主点，要先计算出圆曲线的要素。

•（一）圆曲线的主点如图所示：•JD——交点，即两直线相交的点；•ZY——直圆点，按线路前进方向由直线进入曲线的分界点；•QZ——曲中点，为圆曲线的中点；•YZ——圆直点，按线路前进方向由圆曲线进入直线的分界点。

•ZY、QZ、YZ三点称为圆曲线的主点。

•（二）圆曲线要素及其计算•T——切线长，为交点至直圆点或圆直点的长度；•L——曲线长，即圆曲线的长度（自ZY经QZ至YZ的弧线长度）；•E0——外矢距，为JD至QZ的距离。

•T、L、E0称为圆曲线要素。

•——转向角。

沿线路前进方向，下一条直线段向左转则为；向右转则为。

•R——圆曲线的半径。

•、R为计算曲线要素的必要资料，是已知值。

单圆曲线详细测设曲线详细测设是指为满足施工要求，利用主点桩放样曲线上中线桩的工作。

中桩间距的要求：平曲线上中桩间距宜为20 m；当地势平坦且曲线半径大于800 m时，其中桩间距可为40 m；一般公路的曲线半径较小，应按测规要求钉设，中桩间距一般为5 m或10 m。

圆曲线要求设桩位置为从曲线起点（终点）算起，第一点的里程应凑成整数桩号，并为中桩间距的整倍数，然后按整桩号设桩。

例如：ZY里程为K18＋197.36，中桩间距为20 m，第1点里程为K18＋200，第2点为K18＋220，…以此类推。

（里程符号铁路为定线里程冠以DK、公路冠以K。

）一、切线支距法切线支距法（直角坐标法）是以ZY或YZ为坐标原点，以切线为x轴，且指向交点为x轴正向，过原点的半径方向为y轴，建立切线坐标系。

利用在这一坐标系内曲线上各点的直角坐标值测设点的平面位置的方法称切线支距法。

1.坐标计算公式如图4.4.1所示，各点的坐标（xi ，yi）按下式计算：式中 li——待测点里程桩号；φi ——li所对圆心角；lA——ZY或YZ里程桩号。

【例4.4.1】按例4.3.1计算成果，圆曲线要求每20 m测设1点，且桩号为整桩号，现以DK18＋200、DK18＋220为例说明计算方法。

【解】（1）根据式（4.4.2）计算各弧长il所对圆心角：（2）根据式（4.4.1）计算各点的直角坐标：2.测设方法（1）置镜于ZY或YZ照准切线，沿切线方向测设横坐标xi，得待测点垂足。

（2）在各垂足点上用量角器，分别定出垂足方向，量取纵坐标yi即可定出各待测点的位置。

（3）测量相邻各桩之间的距离，并与相应桩号间的距离进行比较，其精度应满足规范要求。

这种方法适用于平坦地区，优点是积累误差小。

二、偏角法1.偏角法测设圆曲线的基本原理偏角法是传统曲线详细测设的方法之一。

偏角是指过置镜点的切线与置镜点到测设点的弦长之间的夹角，几何学中称为弦切角。

如图4.4.2所示，偏角法测设曲线的基本原理是根据偏角δ和弦长C交会出曲线点。

曲线测设实验报告曲线测设实验报告一、引言曲线测设是土木工程中常用的一种测量方法，用于确定地面或建筑物的曲线形状和位置。

通过测量曲线的各个要素，可以为工程设计和施工提供准确的数据和参考依据。

本实验旨在通过实际操作，掌握曲线测设的基本原理和方法。

二、实验目的1. 了解曲线测设的基本概念和测量要素；2. 掌握使用测量仪器进行曲线测设的方法；3. 学会处理和分析曲线测设的测量数据；4. 提高实际操作和团队协作能力。

三、实验仪器和材料1. 全站仪：用于测量角度和距离的仪器；2. 三脚架：用于支撑全站仪的支架；3. 测量杆：用于测量高差和距离的标尺；4. 曲线测设示意图：用于实际操作的参考图。

四、实验步骤1. 设置全站仪首先，将全站仪放置在三脚架上，并调整水平。

接下来，使用全站仪的调节装置，使望远镜准确对准基准点，并记录基准点的坐标。

2. 测量曲线要素根据曲线测设示意图，确定需要测量的曲线要素，如切线点、曲线半径、曲线长度等。

使用全站仪测量仪器，测量各个要素的角度和距离，并记录下来。

3. 计算和分析数据根据测量数据，使用相关公式和计算方法，计算出曲线要素的具体数值。

例如，可以使用三角函数计算出切线点的坐标，使用勾股定理计算出曲线长度等。

4. 绘制曲线图根据计算结果，使用绘图工具绘制曲线图。

可以使用计算机辅助设计软件，也可以手工绘制。

曲线图应准确反映实际测量结果，并标注各个要素的数值。

五、实验结果与分析根据实际操作和数据处理的结果，我们成功测量了给定曲线的各个要素，并绘制了相应的曲线图。

通过分析数据，我们可以得出以下结论：1. 曲线的半径对于曲线的形状和曲率起着重要的影响。

较小的曲线半径意味着更弯曲的曲线，而较大的曲线半径则意味着较为平缓的曲线。

2. 曲线的长度是曲线测设中的一个重要参数。

在设计和施工过程中，需要准确测量曲线的长度，以确定所需的材料和工作量。

3. 切线点是曲线上一个重要的控制点，用于确定曲线的起点和终点。

第三节圆曲线的详细测设§11—3 圆曲线的详细测设一、偏角法测设圆曲线圆曲线的主点ZY、QZ、YZ定出后,为在地面上标定出圆曲线的形状,还必须进行曲线的加密工作。

曲线点：对圆曲线进行加密，详细测设定出的曲线上的加密点。

曲线点的间距：一般规定,R≥150m时曲线点的间距为2Om，50m≤R<150m时曲线点的间距为10m 。

R<50m时曲线上每隔5m测设一个细部点；在点上要钉设木桩,在地形变化处还要钉加桩。

曲线测设：设置曲线点的工作，常用的方法有:偏角法和切线支距法。

1. 偏角法的测设原理：1）偏角：即弦切角2）原理：根据偏角（δ1）及弦长（c）测设曲线点。

如图11-4：从ZY点出发,根据偏角δ1及弦长C（ZY-1）测设曲线点1;根据偏角δ2及弦长C（1一2）测设曲线点2… 等。

2．偏角及弦长的计算：（1）偏角计算：原理：偏角(弦切角)等于弦所对应的圆心角的一半。

如图11-4，ZY-1曲线长为K,所对圆心角：则相应的偏角：当所测曲线各点间的距离相等时,以后各点的偏角则为第一个偏角δ1的累计倍数。

即：（2）弦长计算(如图11-4)严密计算公式：※弦弧差（弦长与其相对应的曲线长之差）:弦弧差=K i– C i = L i3/ (24R2)当R=450m时，20m的弦弧差为2mm，∴当R>400m时，不考虑弦弧差的影响。

由于铁路曲线半径一般很大, 20m的弦长与其相对应的曲线长之差很小,就用弦长代替相应的曲线长进行圆曲线测设。

近似计算：整弦：里程为20m倍数的两相邻曲线点间的弦长（曲线点间距20m对应的弦长）。

分弦：有一端里程不为20m倍数的两相邻曲线点间的弦长。

（通常要求曲线点设置在整数里程上（如20m的倍数）,即里程尾数为00, 20, 40, 60, 80m等点上，但曲线的ZY点、QZ 点、YZ点常不是整数里程,因此在曲线两端及中间出现分弦）。

例如：在前面例题中，ZY的里程为37+553.24；QZ的里程为37+796.38;YZ的里程为38+039.52,因而曲线两端及中间出现四段分弦。

简述单圆曲线主点测设方法(一)简述单圆曲线主点测设引言在道路建设和测量工程中，测量曲线是非常重要的一环。

而其中的主点测设，更是曲线测量的核心部分。

本文将详细介绍单圆曲线主点测设的各种方法。

目录•直角坐标法•反射投影法•柱面曲线法直角坐标法直角坐标法是主要应用于平面曲线的测设方法之一。

该方法的主要步骤包括： 1. 在合适的比例尺下，绘制曲线外观图。

2. 根据设计要求，确定曲线的起点与终点坐标。

3. 确定曲线的中点坐标。

4. 根据曲线的半径和角度，计算各个主点的坐标。

5. 将计算得到的坐标标注在曲线外观图上，以便后续施工。

反射投影法反射投影法适用于在地面上进行曲线测设的情况。

具体步骤如下：1. 在合适的地方，建立起始点与终止点的测量基线。

2. 使用测距仪等测量设备，测量起始点与终止点到基线的距离，得到X与Y坐标。

3. 绘制基线上的等距线段，并在等距线段上确定主点位置。

4. 使用反射仪将主点的位置反射到地面上，形成一个可见的标记。

5. 使用测量设备测量反射点与基线之间的距离，得到曲线点的坐标值。

柱面曲线法柱面曲线法适用于在实际建设中需要考虑地形高差的情况。

具体步骤如下： 1. 在曲线外观图上，确定起点、终点和中点的坐标。

2. 确定曲线的设计半径和设计点的升高。

3. 根据设计点的升高和曲线半径，计算每个主点的升高。

4. 将每个主点升高后的坐标标注在曲线外观图上。

5. 使用测高仪等设备，分别测量每个主点的实际高差，并进行修正。

结论单圆曲线主点测设是进行道路测量和建设的关键步骤之一。

通过直角坐标法、反射投影法和柱面曲线法等不同的测设方法，可以准确确定曲线的主点坐标，为后续的施工与设计提供准确的数据支持。

每种方法都有其适用的情况，测量人员应根据具体情况选择最合适的方法进行测量。

直角坐标法详解直角坐标法是主要针对平面曲线测设的一种方法。

其具体步骤如下：1.曲线外观图绘制：在合适的比例尺下，绘制曲线的外观图，包括起点、终点和中点。

圆曲线的测设步骤
圆曲线的测设步骤一般包括以下几个步骤：
1. 准备工作：确定测设区域，安全标识设置，仪器检查和校准等准备工作。

2. 建立基线：根据需要选择起点和终点，建立一条基线作为测设的起点。

3. 设置测设仪器：根据测设的需求，选择合适的测量仪器，并进行仪器的设置，包括放置测量仪器的位置和高度等。

4. 量测点的布置：在测设区域内按照一定的间距设置测量点，可以使用测量杆或其他标志物进行标记。

5. 进行测量：使用测量仪器进行测量，可以采用全站仪或其他适用的测量工具。

根据测量仪器的说明和操作步骤，进行相应的测量。

6. 数据处理与计算：将测得的数据导入计算机进行数据处理和计算，得到所需的测量结果，包括曲线半径、切线长、圆曲线长度等。

7. 绘制测量图：将测设结果绘制成测量图，包括圆曲线曲线图、水平曲线图和纵断面图等。

8. 检查和验收：对测设结果进行检查和验收，确保测量结果的
准确性和可靠性。

需要注意的是，在进行圆曲线测设时，需要遵循相关的测量规范和标准，保证测量的精度和准确性。

同时，在测设过程中要注意安全，遵守相关的安全操作规范，确保测量人员和周围环境的安全。