03-画法几何及工程制图-第3章-投影变换

《画法几何与工程制图》课程教学大纲课程名称：画法几何与工程制图课程代码：课程类型:专业必修课学分：3 总学时：64 理论学时：32 实验学时：32 先修课程：无适用专业:工程管理一、课程性质、目的和任务画法几何与工程制图是工程管理专业的必修课程。

学习画法几何与工程制图课程的目的是培养学生绘制和阅读建筑工程图的基本能力，是通过画法几何及制图理论的学习和建筑工程制图实训的实践，培养正确使用绘图仪器和徒手作图能力，熟悉建筑制图国家标准的规定，掌握并应用各种图示方法来表达和阅读建筑工程图，本课程的主要任务是：通过让学生掌握制图及投影的基本知识，掌握建筑图样的画法，培养专业识图的基本能力，培养空间想象能力和空间表达能力，培养学生认真负责的工作态度和严谨细致的工作作风，为学习计算机绘图及后续专业课程打下良好的基础。

二、教学基本要求1、知识、能力、素质的基本要求：（1）明确本课程的地位、性质、任务和学习方法。

（2）培养用仪器绘图、徒手绘图的基本技能。

（3）学习用正投影法表达空间几何形体的基本原理和方法。

（4）培养绘制与阅读投影图的能力。

（5）培养适度与绘制建筑施工图、结构施工图、钢筋混凝土构件图等施工图的基本能力。

2、教学模式基本要求本课程采用理论教学和实验教学交叉进行的教学方式，授课方式为多媒体教学，精心设计课堂教学环节，如讲授、练习、制图、讨论等多种实践活动。

实践课以学生动手画图、识图为主，在掌握基本理论基础上增加制图、识图的能力，注意教与学之间的信息沟通与反馈。

三、教学内容及要求1 绪论教学内容：1.1 画法几何及土木工程制图课程概述1.2 投影的基本知识1.3 画法几何及土木工程制图的发展史和发展方向教学要求：（1）了解画法几何与土木工程制图的课程性质及画法几何及土木工程制图的发展史和发展方向；（2）掌握投影的基本知识。

2 画法几何教学内容：2.1 点2.1.1 点在三面体系第一角中的投影与该点的直角坐标关系2.1.2 点在两面体系第一角中的投影2.1.3 两点的相对位置2.2 直线2.2.1 直线的投影以及直线对投影面的各种相对位置2.2.2 直线上的点的投影特性2.2.3 求直线的真长及其对投影面的倾角2.2.4 两直线的相对位置2.2.5 两直线垂直2.3 平面2.3.1 平面的表示法2.3.2 平面对投影面的各种相对位置2.3.3 平面上的点、直线和图形2.4 直线与平面以及两平面的相对位置2.4.1 直线与平面以及两平面平行2.4.2 直线与平面以及两平面相交2.4.3 直线与平面以及两平面垂直2.4.4 点、直线、平面的综合作图题示例2.5 投影变换2.5.1 投影变换的目的和方法2.5.2 换面法以及用换面法解定位及度量问题示例2.5.3 以投影面垂直线为轴的旋转法简介2.6 曲线、曲面和立体2.6.1 平面立体及其表面上的线和点2.6.2 平面曲线和空间曲线2.6.3 曲面、曲面立体及其表面上的线和点2.6.4 圆柱螺旋线和平螺旋面2.7 平面、直线与立体相交2.7.1 平面与平面立体相交2.7.2 直线与平面立体相交2.7.3 平面与曲面立体相交2.7.4 直线与曲面立体相交2.8 两立体相交2.8.1 两平面立体相交2.8.2 平面立体与曲面立体相交2.8.3 两曲面立体相交2.9 轴测投影2.9.1 轴测投影的基本知识2.9.2 正等测的画法2.9.3 斜等测和斜二测的画法2.9.4 轴测投影的选择2.10 标高投影2.10.1 点和直线2.10.2 平面2.10.3 曲线、曲面和地面2.10.4 应用示例教学要求：（1）掌握点、直线、平面、曲面、立体等的投影的基本原理及其作图方法。

画法⼏何及⼯程制图教案《画法⼏何及⼯程制图》讲稿与教案数理与软件⼯程学院绪论课程名称：画法⼏何及⼯程制图。

课程性质：是⼯科专业的⼀门技术基础课。

画法⼏何是研究在平⾯上⽤图形表⽰形体和解决空间⼏何问题的理论和⽅法的学科。

画法⼏何是机械制图的投影理论基础，它应⽤投影的⽅法研究多⾯正投影图、轴测图、透视图和标⾼投影图的绘制原理，其中多⾯正投影图是主要研究内容。

画法⼏何的内容还包含投影变换、截交线、相贯线和展开图等。

1103年，在中国宋代李诫所著的《营造法式》⼀书中的建筑图基本上符合⼏何规则，但在当时尚未形成画法的理论。

1799年，法国数学家蒙⽇发表了《画法⼏何》⼀书，提出⽤多⾯正投影图表达空间形体。

这为画法⼏何奠定了理论基础。

以后的各国学者⼜在投影变换、轴测图，以及其他⽅⾯不断提出新的理论和⽅法，使这门学科⽇趋完善。

我们知道，任何建筑物及其构件的形状、⼤⼩和做法，都不是⽤普通语⾔或⽂字能表达清楚的。

必须按照⼀个统⼀的规定画出它们的图样，作为施⼯、交流的依据，作为表达设计师构思的⼿段。

因此，⼯程图样被喻为⼯程界的语⾔，是⼯程技术部门的⼀项重要的技术⽂件。

本门课程和⼯程测量被认为是⼯程技术⼈员的两⼤技能。

主要任务：1.学习投影法的基本理论和应⽤；2.培养学⽣空间⼏何问题的图解能⼒；3.培养学⽣的空间想象能⼒和空间思维能⼒；4.认识国标，应⽤国标；5.培养学⽣阅读、绘制⼯程图样的技能；6.培养学⽣的⼯程意识，养成认真负责的⼯作态度和⼀丝不苟的⼯作作风。

学习⽅法：⾸先要多看、多想、多⽐划，尽快建⽴空间概念；其次要知道本门课程就是从点、到线、到⾯、再到体，⼀环扣⼀环，逐步深⼊。

因此，每⼀节课、每⼀章节内容都应该很好地掌握，否则后续章节就⽆法学习。

再者，就是要勤做练习、快做练习。

课后如果不及时完成作业，将会⼤⼤降低学习效率。

另外，要⽤好⽹络课程。

需要说明的是，学好任何⼀门课程，都没有捷径可⾛，都要付出艰⾟的努⼒。

《画法几何及工程制图》作业参考答案（一）第一章1-1.练习长仿宋字。

[p78](自行完成)1-2.数字和字母练习（临摹“画法几何及工程制图”第十一章中的相关字体）。

[p81](自行完成)1-3.在A3幅面的图纸上，用1：1的比例按下列图形练习图线（不注尺寸），图名为“图线练习”。

[p83](自行完成)1-4.按给出的图样画徒手图。

[p85]（自行完成）第二章点、线、面投影2-1.根据点的空间位置，画出点的投影图。

[p1]（答案略）2-2.根据点到投影面的距离，画出点的三面投影图。

（答案略）ab”A AA BBB c ׳2-3.根据点的坐标，画出点的投影图和空间位置。

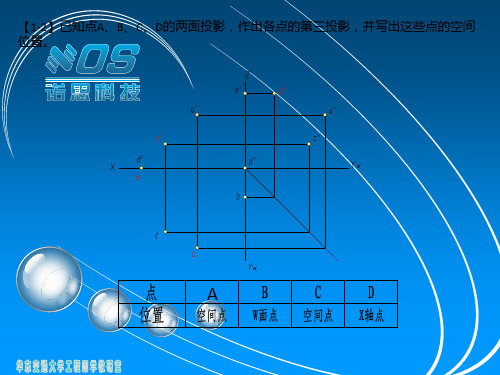
[p2]（答案略）2-4.根据点的两面投影求第三投影，并判定其相对位置。

[p3]b' bb”c' c” c ( a” ) ( )2-5.已知点B 在点A 的正上方10，点C 在点B 的正左方10，求A 、B 、C 的三面投影，并标明其可见性。

[p4]2-6.已知长方体的投影图，试判定棱线AB 、AC 、CD 与投影面的相对位置，并标明其侧面投影。

[p4]（答案见复习题）2-7.注出三棱锥SABC各棱线的水平和正面投影，并判定它们属于哪类直线。

[p5]（答案见复习题）2-8.求直线AB、CD和EF的第三投影。

[p6]2-9.分别求出直线CD和EF的实长及其倾角α和β。

[p7]2-10.已知直线AB与V面的倾角β=300，求其水平投影ab。

[p7]2-11.判定点K是否在直线AB上。

[p7] 提示：用点分线段成定比的方法判定b2-12.判定下列直线的相对位置（平行、相交、交叉）。

[p7]（答案见复习题）2-13.求点M到直线AB的距离。

[p8]2-14.求一距H面为20的水平线，与两交叉直线AB、CD相交。

[p8]2-15.判定两条交叉直线AB、CD对V、W面重影点的可见性。

[p8]2-16.试求两条直线AB、CD之间的距离。

土木类《画法几何与工程制图》课程教学大纲Descriptive Geometry and Engineering Drawing课程编号：适用专业：土木、路桥、给排水、建筑设备、土地资源管理等专业学时数：72-80学时（含上机14~20学时）学分数： 5～6分散实验学时：36～40学时（约为总学时的一半）执笔者：罗康贤，左宗义编写日期：2004年3月一、课程的性质和目的：1、本课程的性质：《画法几何与工程制图》研究绘制和阅读工程图样以及解决空间几何问题的理论和方法。

所谓工程图样，是工程与产品信息的载体，是工程界表达、交流的语言。

本课程理论严谨，实践性强，与工程实践有密切的联系，对培养学生掌握科学思维方法，增强工程意识和锻炼独立工作能力有重要作用，是普通高等院校本科土木类或近土木类专业必修的技术基础课程。

2、本课程的目的：1、培养使用投影的方法用二维平面图形表达三维空间形状的能力。

2、培养对空间形体的形象思维能力。

3、培养创造性构型设计能力。

4、培养仪器绘制、徒手绘画和阅读专业图样的能力。

5、培养贯彻、执行国家标准的意识。

6、培养使用绘图软件绘制与本专业相关的工程图样的能力。

此外，在教学过程中还要注重培养学生的自学能力、科学作风，分析问题和解决问题能力以及创新意识，提高学生的全面素质。

二、课程教学内容：本课程的内容结构分为三部分：工程图学基础（包括投影理论等画法几何部分）、工程制图（主要包括表达方法和专业工程图样的绘制与阅读）与计算机绘图，后两部分因专业类别不同而稍有不同侧重。

（一）第一部分：工程图学基础（44～54学时）第一章制图基本知识和技能（2～4学时）本章基本要求：1、了解现行国家标准《技术制图》和《建筑制图》中有关基本规定。

2、掌握手工绘图工具及其使用方法。

3、掌握几何图形的画法。

4、掌握平面图形的尺寸分析及画法。

本章知识点为：国标的基本规定第二章投影的基本知识（6～8学时）本章基本要求：1、了解投影法的基本概念、投影法的分类。

3.1 点3.2 直线3.3 平面3.4 直线与平面、平面与平面的相对位置任何物体的表面都可以看成是由点、线和面所组成，任何复杂的空间几何问题都可以抽象成点、线、面的相互关系问题。

因此，要正确、迅速地画出物体的投影和分析空间几何问题,须掌握点、线、面的表示方法和投影性质。

过空间点A的投射线与投影面P的交点a称为点A在投影面P上的投影。

仅有点的一个投影不能确定点的空间位置。

点的投影a可以是过a的投射线上任一点（如A、A1、A2等）的投影。

正投影法采用多面正投影来确定点的空间位置。

点A在V/H两投影面体系中的投影:根据正投影的原理，已知点A的水平投影及正面投影则可确定点A的空间位置。

因此，点的两面投影即可完全确定点的空间位置。

1.点的三面投影2.点的投影规律投射线Aa和Aa′构成平面Aaa x a′，因Aa⊥H面，Aa′⊥V面则Aaa x a′⊥H面，又⊥V面因三平面互相垂直，其交线必互相垂直，故a′a x⊥OX，aa x⊥OX投影面展开后，得a′a⊥OX，又因Aaa x a′是一矩形，故aax=Aa′=点A至V面的距离a′a x=Aa=点A至H面的距离同理可得：a′a″⊥OZa′az=Aa″=点A至W面的距离a″a z=Aa′=点A至V面的距离2.点的投影规律综上所述，点的三面投影规律是：(1)点的正面投影与水平投影的连线垂直于OX轴；点的正面投影与侧面投影的连线垂直于OZ轴；点的水平投影到OX轴的距离等于点的侧面投影到OZ轴的距离。

即：a′a⊥OX；a′a″⊥OZ；aa x= a″a z(2)点的投影到投影轴的距离，等于该点到另一投影面的距离。

即：a′a x= a″a y W= Aa (点A至H面的距离)；aa x= a″a z= Aa′(点A至V面的距离)；a′a z= aa y H= Aa″(点A至W面的距离)。

2.点的投影规律3.点的投影与直角坐标的关系互相垂直的三个投影轴构成一个空间直角坐标系，空间点A的位置可以用坐标值A（x,y,z）表示。