当前位置：文档之家 › 立体上点的三面投影

立体上点的三面投影

  • 格式：ppt
  • 大小：1.11 MB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

2-2 点、线、面的投影特性

2-2 点、线、面的投影特性

2-2 点、线、面的投影特性一、点的投影1、点的三面投影点是组成物体最基本的几何元素。

如图2-9所示，在三投影面体系中，由空间点A（x，y，z）分别向三投影面作正投影，得其三面投影a（x，y）、a′(x，z）、a″（y，z），即过点A分别作三投影面的垂线，其垂足即为点A的三面投影；展开H面和W面，得到点A的三视图：a 、a′长对正，a′、a″高平齐，a 、a″宽相等，如图2-10所示。

图2-9 点的三面投影图2-10 点的三视图例1 ：已知空间点B的两面投影b ，b′，如图2-11所示，求其第三面投影b″。

分析：空间点B的三面投影b 、b′、b″符合“长对正，高平齐，宽相等”的投影规律。

作图： b′与b″高平齐，b与b″宽相等，则其交点即为b″。

图2-11 求点的第三面投影图2-12 求点的三面投影例2 ：已知空间点D(5,4,3)，如图2-12所示,求其三面投影。

分析：空间点D的三面投影分别为d（x，y）、d′（x，z）、d″（y，z），且符合“长对正，高平齐，宽相等”的投影规律。

作图：分别在三投影轴上取x1=5，y1=4，z1=3，按“长对正，高平齐，宽相等”的投影规律分别作直线段，交点即为空间点D的三面投影（d 、d′、d″）。

2、两点的相对位置空间两点的相对位置是指空间两点间前后、左右、上下的位置关系。

两点在空间的相对位置可以根据两点的坐标值来判定，如图2-13所示。

X坐标确定两点的左右位置关系。

X坐标值大的点在左；Y坐标确定两点的前后位置关系。

Y坐标值大的点在前；Z坐标确定两点的上下位置关系。

Z坐标值大的点在上。

图2-13 两点的相对位置故A点在B点的右，后，上方，即B点在A点的左，前，下方。

3、重影点及其可见性判断若空间两点在某一投影面上的投影重合，则称这两点为该投影面的重影点。

此时，这两点位于同一投射线上，且有两个坐标的值分别相等，不等值的坐标之大小可以确定重影点的可见性，即X、Y、Z坐标值大的点分别位于左方、前方、上方，为可见点，如图2-14所示。

第二章 投影的基本知识3

第二章 投影的基本知识3

空间点到W面的距离为x坐标； 空间点到W面的距离为x坐标；即：Aa〞=a′az=aaYH=x坐标 空间点到V面的距离为y坐标； 空间点到V面的距离为y坐标；即：Aa′=aax=a〞az=y坐标 空间点到H面的距离为Z坐标； 空间点到H面的距离为Z坐标；即：Aa=a′ax=a〞aYW=Z坐标
• 空间点及投影位置即可用坐标方法表示，如点A的空 空间点及投影位置即可用坐标方法表示， 间位置是： ）；点 间位置是：A（x，y，z）；点A的H面投影是a（x，y， ），点 ，），点 0），点A的V面投影a′（x，0，z，），点A的W面投 ，）。应用坐标能较容易地求作点 影a〞（0，y，z，）。应用坐标能较容易地求作点 的投影和指出点的空间位置。 的投影和指出点的空间位置。
（ b）过b作OX轴的 ） 作 轴的 垂线 bbx并延长之 并延长之
（c）过b〞作OZ轴的垂 ） 〞 轴的垂 并延长之， 线b〞bz并延长之，与bbx 〞 并延长之 延长线相交于b′点即为所求 延长线相交于 点即为所求
例【1-2-2】：已知空间点C的H面投影c和V面投影c′， 已知空间点C 面投影c 面投影c′， c′ 求作点C 面投影c 求作点C的W面投影c〞。 • 【解】：如图1-2-22所示， 如图1 22所示 所示，
(a)画出投影轴； 画出投影轴； 画出投影轴
轴上量取Obx=x=20 （b） 在OX轴上量取 ） 轴上量取 轴上量取ObYH=y=0 在OYH轴上量取 轴上量取 轴上量取Obz=z=10 在OZ轴上量取 轴上量取
（d）因 ） obYH=obY W=0，所b〞 〞 重合。 与bz重合。 重合
轴的垂线， （c）过bx作ox轴的垂线， ） 作 轴的垂线 轴的垂线， 过bz作oz轴的垂线， 作 轴的垂线 得交点b和 得交点 和b′ 从上例B点的投影图中反映了一个规律 见图1-2-26 点的投影图中反映了一个规律： 从上例 点的投影图中反映了一个规律：见图 如空间点位于投影面上（ 如空间点位于投影面上（即点的三个坐标中有一个 坐标等于零）， ），它的三个投影中必有两个投影位于 坐标等于零），它的三个投影中必有两个投影位于 投影轴上，反之，空间一个点的三个投影中， 投影轴上，反之，空间一个点的三个投影中，如果 有两个投影位于投影轴上， 有两个投影位于投影轴上，该空间点必定位于某一 投影面上。 投影面上。 图1-2-26

天大《工程制图基础》学习笔记二

天大《工程制图基础》学习笔记二

主 题：《工程制图基础》学习笔记内 容：《工程制图基础》学习笔记二第二章正投影法基础2.1正投影法2.1.1投影法和投影投射线通过物体，向选定的平面投射，并在该面上得到图形的方法 ，称为投影法。

根据投影法所得到的图形，称为投影。

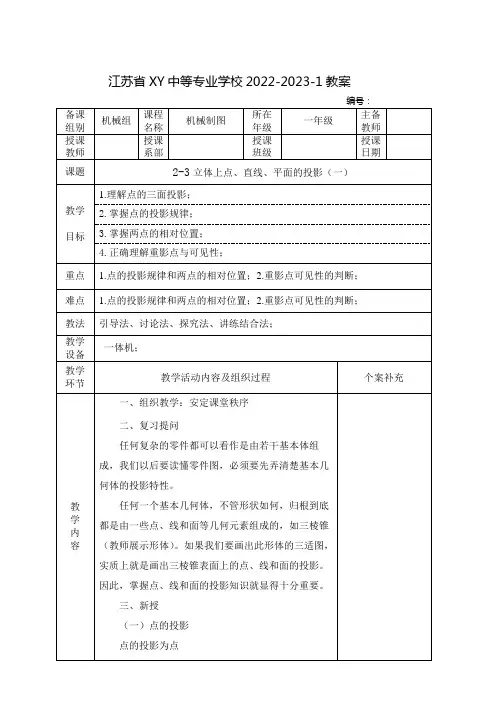
2.1.2投影法分类⑴中心投影法投射线汇交一点的投影法称为中心投影法。

图2-1中心投影法⑵行投影法投射线相互平行的投影法称为平行投影法。

斜投影法：S倾斜于P正投影法：S⊥P（a）斜投影法 （b）正投影法图2-2平行投影法2.1.3正投影法的投影特点（1）平面图形或线段平行于投影面时，其投影反映实形或实长。

如图2-3（a）所示。

（2）当平面图形或线段垂直于投影面时，其投影为一直线或一点。

（积聚性）如图2-3（b）所示。

（3）平面图形或线段倾斜于投影面时，其投影为类似形。

如图2-3（c）所示。

图2-3正投影法的投影特点2.1.4物体的三面投影图物体的单面投影不能完全表达其形状，工程图样用多面正投影表达物体，最常见的是三面投影。

（1）三面体系的形成三个两两互相垂直的投影面组成三面体系（2）物体在三面体系中的放置使物体上尽可能多的表面平行或垂直于投影面（3）体在三面体系中的投影：正面投影、侧面投影、水平投影。

如图2-4所示。

图2-4物体的三面投影（4）三面体系的展平—三面投影图。

如图2-5所示。

（5）三面投影的投影规律。

如图2-5所示。

正面投影和水平投影 长对正正面投影和侧面投影 高平齐水平投影和侧面投影 宽相等图2-5三面投影的形成和投影规律2.2立体上点的投影2.2.1立体上点的三面投影。

如图2-6所示。

点的三面投影就是从点分别向三个投影面所作垂线的垂足。

点的三面投影同样遵守“长对正、高平齐、宽相等”的投影规律。

图2-6立体上点的投影2.2.2立体上两点的相对位置立体上两点的相对位置是指这两点在空间的左右（X）、前后（Y）、上下（Z）三个方向上的相对位置。

如图2-7所示。

图2-7立体上两点的相对位置2.3立体上直线的投影2.3.1直线的投影 如图2-8所示。

中职机械制图教案：立体上点、线、面的投影(全3课时)

中职机械制图教案：立体上点、线、面的投影(全3课时)

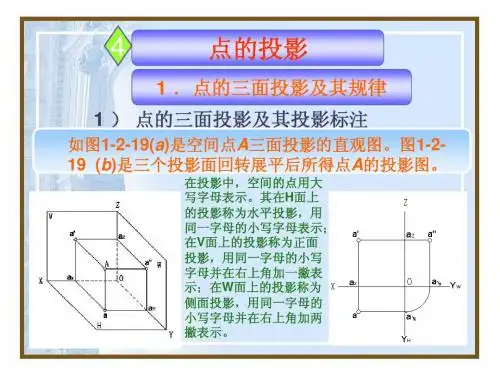
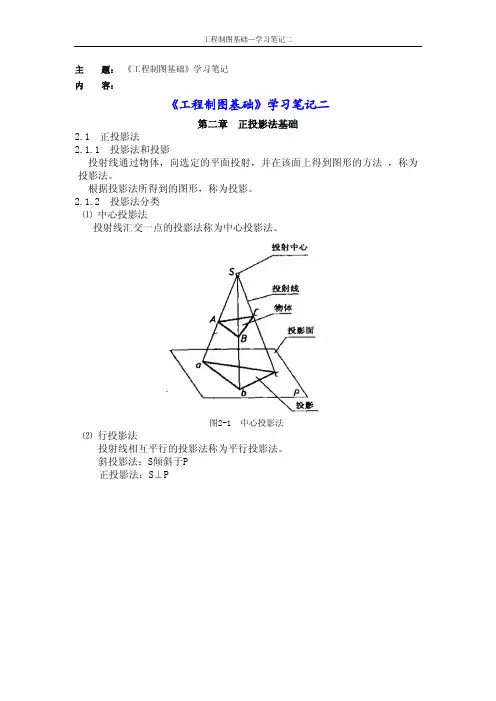
江苏省XY中等专业学校2022-2023-1教案教学内容1.点的三面投影习惯上我们将空间点用大写的字母表示，其投影用相应的小写字母表示。

空间点A的位置确定后，那么它的三面投影（a、a′、a″）投影就确定了，反之如果空间一点的三面投影确定，则空间点的位置也就确定。

2.点的三面投影规律（教师要注意解释）aa′⊥OX；a′a″⊥OZ；a′a yH= a″a yE点的投影规律与“长对正、宽相等和高平齐”是一致的。

3.点的投影和直角坐标系的关系A（x、y、z）空间A点到W面的距离为坐标X，即A→W=x；空间A点到V面的距离为坐标X，即A→V=y；空间A点到H面的距离为坐标X，即A→H=z。

空间点A与其坐标（x、y、z）式一一对应的关系，同样空间点A与其三面投影（a、a′、a″）也是一一对应的关系，从而我们可以得出点的投影与点的坐标也存在着一定的联系。

即水平投影a→(x、y)；正面投影a→(x、z)；侧面投影a→(y、z)教学内容教师提问：点的三个坐标值与点的位置有什么样的关系？即坐标值为多少时，点在空间？点在投影面上？点在投影轴上？点在原点？例题1：已知点A的V面投影a'和W面投影a X，求作H面投影a。

分析：根据点的投影规律可知：aa′⊥OX，过a′点作OX轴的垂线a′a X,所求a必定在a'a X的延长线上。

由aa X= a″a z，可确定a在a′a X延长线上的位置。

作图：（1）过a′作a′a X⊥OX并延长，如图2-14b所示。

（2）量取aa X= a″a z，可求得a。

也可如图2-14c 所示，利用45。

线作图。

4.两点的相对位置前面我们已经知道点在空间里的位置可由其坐标值来确定，假如空间里有两点A和B，那么它们之间的位置关系又如何确定？空间两点的位置关系可由两点的同名坐标值的差来确定。

如xA>xB、yB>yA、zA>zB，则点A在点B的左边、后面和上面。

例题2：已知空间点C（16，5，6），点D在点C 之右10mm、之前7mm、之上8mm，求作C、D两点的三面投影，如图2-16所示。

第三章-点、线、面的投影

第三章-点、线、面的投影

1、水平投影积聚为一直线，并
（1）铅垂面
反映对V、W面的倾角β、γ的实
为一条直线并平行于相应的投 影轴。
Z
r'
r"
Q
r" W X
X
O
r
r
H Y
O
YW
YH
（3）迹线平面
1、无侧面迹线； 2、RH//OYH轴，RV//OZ 轴，有积聚性。
总结
投影面平行面的投影特性可概括如下： （1）平面在它所平行的投影面上的投影反映实形； （2）平面在另外两个投影面上的投影积聚成直线， 且分别平行于相应的投影轴。
（5）平面图形[△ABC]
不但能确平面的 位置，而且能表 示平面的形状和
大小。
2、用迹线表示平面 迹线：平面与投影面的交线。 迹线平面：用迹线来表示的平面。
水平迹线：P平面与H面的交线，用PH表示 正面迹线：P平面与V面的交线，用PV表示 侧面迹线：P平面与W面的交线，用PW表示
用迹线表示平面
YH
可得出点的投影特性如下：
（1）点的投影的连线垂直于相应的投影轴。 （2）点的投影到投影轴的距离，反映该点到相应的投影面 的距离。
一般只画出投影轴，不画 投影面的边框
【例3-1】 已知点A的水平投影a和正面投影a′，求其 侧面投影a″
解: 作图步骤如下
二、点的投影与坐标
1、投影与坐标
引入直角坐标系的概念，点A的空间位置可用直角坐标表 示为A（x，y，z），其中x表示A点到W面的距离，y表示 A点到V面的距离，z表示A点到H面的距离。
直线与投影面垂直 直线与投影面平行 直线与投影面倾斜
一、投影面平行线
定义：平行于一个投影面，同时倾斜于其它两个投影 面的直线。

机械制图-点、直线、平面的投影

机械制图-点、直线、平面的投影
特殊位置点的应用
在机械制图中，特殊位置点常用于 确定物体的形状和大小，如交点、 切点等。
03 直线投影
直线在三投影面体系中的投影
正投影
直线在正投影面上的投影 与原直线平行或重合，且 长度不变。
侧投影
直线在侧投影面上的投影 与原直线垂直，且高度不 变。
水平投影
直线在水平投影面上的投 影与原直线平行，且长度 不变。
直线上的点的投影特性
点在直线上
点的投影在直线的投影上，且与 原点在同一平面内。
点在直线外
点的投影在直线的投影外，且与 原点不在同一平面内。Leabharlann 两直线的相对位置与投影特性
平行线
两直线在正投影面上的投影平行， 且高度相等。
交叉线
两直线在正投影面上的投影相交， 且高度相等。
垂直线
两直线在正投影面上的投影垂直， 且高度相等。
机械制图-点、直线、平面的投影
目 录
• 引言 • 点投影 • 直线投影 • 平面投影 • 实际应用与案例分析 • 总结与展望
01 引言
主题简介
01
机械制图是工程领域中用于表达 和交流设计思想的一种语言，而 点、直线和平面的投影是机械制 图的基础。
02
本主题将介绍点、直线和平面在 机械制图中的投影原理和方法， 帮助读者更好地理解和应用机械 制图。
投影法概述
投影法是将三维物体转换为二维图形 的方法，是机械制图中的基本技术。
投影法分为中心投影法和平行投影法 ，其中平行投影法又分为正投影法和 斜投影法。
02 点投影
点在三投影面体系中的投影
点的三面投影
一个点在三投影面体系中分别在H面、 V面和W面上投下影子，形成三个投 影点。

点的三面投影规律

点的三面投影规律

二、点的三面投影与直角坐标的关系
为了研究问题方便，可将三投影面体系视为一空间直角坐标 系。这样就可将 H 、 V、 W 三投影面视为坐标平面， X 、 Y、 Z 三 投影轴视为坐标轴，投影原点O视为坐标原点。
引入坐标系的概念后，就可用坐标说明点的位置。
三个有序的坐标即X、Y、Z可确定惟一一个点的位置 点的坐标表示方法：A（X，Y，Z）例如：A（15，20，8）、B（5，30，25）
根据给出的两点的坐标判断相对位置。 两点中，X坐标大的点在左；Y坐标大的点 在前；Z坐标大的点在上。
试判别图中A、B两点的相对位置。
A点在B点之上方 、 后方、 右方 点的坐标是作点的投影图和判断两点间 位置关系的基础，也是分析和解决空间问题 的关键。 应充分理解点的投影与其坐标的关系， 尤其要熟悉三投影面的转换规律。
例3.已知B点的两面投影，补出B点的第三投影。 作图分析：由于点的任两投影都能反映 该点的三个坐标，因此便可按点的投影 规律作出点的第三投影。
作图步骤：
1.按点的投影规律作点的投影连线 2.投影连线的交点即为B点的水平投影
四、两点的相对位置
两点间的相对位置是指空间两点之间的上下、左右和前后的位置 关系。 判断方法：
2.过ax、ay和az点作相 应坐标轴的平行线，各线 的交点为点的投影
3.分别过a、a'、a''作 三坐标轴的平行线，三 条线的交点为空间A点
例2: 已知B（40、30、0）作出B点的三面投影。 问题：根据B点的坐标分析B点的位置。 因B点的坐标（40、30、0）中Z坐标为0，故B点位于H面上。
点的位置有如下说法：
1.空间的点，如图中的A点 2.投影面上的点，即位于V、H 或W投影面上，如B点 投影面上的点的三个坐标中有一个为0

点的三面投影及其投影特性-教学设计

点的三面投影及其投影特性-教学设计

课题1：点的三面投影及其投影特性教学设计方案一、教学思想根据目前教育“以就业为指导、以能力为本位、以技能为核心”的教学原则，将培养学生关键能力（即自我或个人能力、社会能力、方法能力以及专业能力）作为重点的指导思想，结合学生认知事物的规律，将教学目标确定如下：二、教学目标与要求1、知识与能力知识目标：通过学习，理解三视图的形成过程，熟练掌握点的投影规律。

能力目标：1、培养学生理论结合实际的学习方法，初步建立平面图形和空间立体图形的转换关系。

2、引导学生培养做事要从基础开始的踏踏实实的良好习惯。

2、过程与方法使学生理解点的投影规律，理解点的坐标与三投影面的关系，能熟练运用“三等关系”绘制点的三面投影。

3、情感与态度让学生通过亲自动手作图，体验成功，在不断尝试中激发求知欲，在不断摸索中陶冶情操。

三、教学重、难点1、教学重点正投影法中点的投影规律处理措施：系统串讲知识点，使学生建立易于理解、便于记忆的知识框架，从生活中接触到的影子为切入点，引入本章该节内容。

2、教学难点根据点的投影规律画点的三面投影处理措施：根据本节课的特点和学生的认知水平，我主要采用讲授法来使学生获取新知识并且在课堂上让学生通过练习来深化对知识的理解。

在总结的时候尝试让学生先讨论再请学生代表进行总结，更好地提高课堂效率。

四、教学策略、教学方法与手段创设任务情境─引导自主探究─进行归纳总结采用任务驱动法，精讲多练，充分将课堂交给学生，以完成一个具体的任务为线索，把教学内容有机贯穿在任务之中，让学生在任务的引领下，经过思考和教师的点拨，积极主动地参与学习，达成教学目标。

（1）任务驱动法：采用任务驱动，带动每位学生参与活动，有利于学生掌握制图过程中的各个环节。

（2）要求学生自己练习，自己分析讲解，让他们在实践的过程中去发现问题，解决问题。

教师在学生练习过程和最后讲评中适当引导。

五、教学过程（含提问、讨论、布置与检查学习任务等）阶段任务教师活动学生活动预期效果奠定基础复习回顾正投影法【复习】上节课，我们主要介绍了正投影法，大家还记得上节课的内容吗？我们先来回忆下：投射线互相平行且垂直于投影面的投影方法，称为正投影法。

建筑制图与识图3立体的投影

建筑制图与识图3立体的投影
3
3.3 切割体的投影
3.3.1 平面切割体的投影
（2）棱面法——面面交线法
将平面立体上参与相交的各棱面， 与截平面求交线，这些交线即围成所 求的平面立体截交线。
3.3 切割体的投影
3.3.1 平面切割体的投影
作图步骤：
1）空间分析及投影分析 a、截平面与立体的相对位置——确定截交线的形状 b、截平面，立体表面与投影面的相对位置——确定截交线的投影特性
PV2
6′ (7′) 7 ′′
例3-8：求作被截五棱柱的三面投影图
4′ (5′) 2′ ( 3′)
PV1
1′
5′′ 3 ′′
6′′
4′′ 2′′ 1′′
3 7(5)
1
2
6(4)
3.3 切割体的投影
3.3.2 曲面切割体的投影
截交线：一般为封闭的平面曲线，特殊情况为直线。 其形状取决于曲面立体的几何特征，以及截平面与曲面立体的相对位置。
c’ （2）绘出圆柱的顶面和底面。
（3）画出正面转向轮廓线和侧面转向轮廓线。
Z
a1’ c1’(d1’) d(d1)
a(a1) c(c1)
d1’
b1’
a1”(b1”) c1’’
c’d’ b’
V a’
D
A
d” B
a”b”
c”W
C
b(b1)
圆柱的投影
正面转向轮廓线 a1’
X
c1’d1’ A1 d(d1)
da11””(b1)”c1” C1b(b1)
曲面上可见与不可见的分界线称为回转面对该投影面的转向轮 廓线，在其他投影面不应画出。
圆柱体的投影
圆柱表面由圆柱面和上下两底面所组成。圆柱面是由一直母线绕与之 平行的轴线回转而成。圆柱上任意一条平行于轴线的直母线称之为素线。

《画法几何及土木工程制图》习题解答

《画法几何及土木工程制图》习题解答
PPT
【11-7】已知由圆锥和圆柱所构成的组合回转体，完成它的正面 投影，并补全其表面上的线段SABCDEFGS的三面投影。
PPT
【11-8】已知由圆柱的左端面和同轴的圆柱面、内环面、球面所 围成的组合回转体，求作它的水平投影，并补全其表面 上的线段ABCDEFGA的三面投影。
PPT
【13-3】作正五棱柱与正垂面P的截交线，补全截断体的三面投影。
PPT
【9-3】已知点D与△ABC平面的距离为12mm，BC为水平线，补全 △ABC的正面投影。
PPT
【9-4】已知点A与直线BC的距离为10mm，求作点A的水平投影。
PPT
【9-5】作两交叉线AB、CD的公垂线，并注明它们之间的最短距离。
PPT
【9-6】已知两交叉直线AB、CD的距离为10mm，补全CD的正面投影。
PPT
【2-3】已知直线AD和点C、B的两面投影，判别C、B是否在 AD上，已知点E在AD上，AE:ED为3：5，作出AD的侧面投影 和点E的三面投影。
PPT
【2-4】作直线AB的真长及其对投影面H、V的倾角α、β，在AB 上作与点A相距25mm的点C的两面投影。
PPT
【2-5】求作直线CD的真长及与投影面V、W的倾角α、β。
【1-1】按照立 体图作诸点的三 面投影。
PPT
A
A
【1-2】已知点A、B、 C、D的两面投影，作出 各点的第三投影，并写 出这些点的空间位置。
B
单击此处输入你的正文， 文字是您思想的提炼， 为了最终演示发布的良 好效果，请尽量言简意 赅的阐述观点。
PPT
【1-3】作出诸点的三面投影：点A(25,15,20)；点B距离投影 面W、V、H分别为20mm、10mm、15mm；点C位于点A之 左10mm、之前15mm、之上10mm；点D在点A之下8mm、 与投影面V、H等距，与投影面W的距离是与H面距离的2.5倍。

机械制造与自动化《点的三面投影》

机械制造与自动化《点的三面投影》

点的三面投影尽管点的两个投影已能确定该点的空间位置，但为了清楚地表达某些几何形体，常需采用三面投影图。

图2-9 三投影面体系图2-10 三投影面体系中点的投影1 三投影面体系三投影面体系是在两投影面体系的根底上，加上一个与H面、V面都垂直的侧立投影面W〔简称侧面〕所组成。

三个投影面互相垂直相交，它们的交线称为投影轴。

V面和H面的交线称为OX轴，H面和W面的交线称为OY轴，V面和W面的交线称为OZ轴。

三个投影轴互相垂直相交于一点O，称为原点，如图2-9所示。

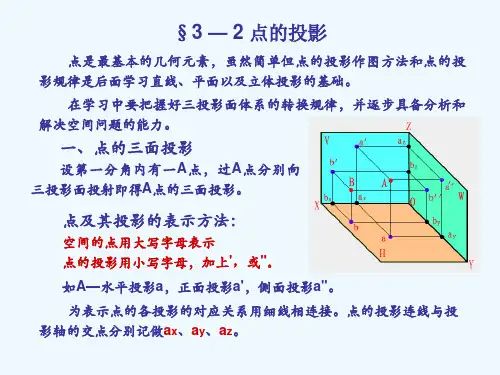
2 点的三面投影设A是三投影面体系中的一点，它在H面和V面上的投影分别为a 和a’。

自点A向W面作垂线，其垂足a〞即为点A在W面上的投影，a〞称为点A的侧面投影，如图2-10所示。

规定点的侧面投影用小写字母加两撇“"〞表示。

绘图时，仍需把三个投影面摊平在一个平面上，为此，规定V面不动，将H面绕OX轴向下旋转90°，将W面绕OZ轴向右旋转90°与V面重合〔随H面旋转的OY轴用OY H表示，随W面旋转的OY轴用OY W表示〕，如图2-11a所示。

然后去掉投影面的边框，即得点A的三面投影图，如图2-11b所示。

a 三个投影面摊平在一个平面上b 点A的三面投影图图2-11 点的三面投影3 点的三面投影规律和分析点的两面投影的投影规律一样，在三投影面体系中点的投影规律是：1〕点的正面投影和水平投影的连线垂直于OX轴，即aa’⊥OX。

2〕点的正面投影和侧面投影的连线垂直于OZ轴，即a’a〞⊥OZ。

3〕点的正面投影到OX轴的距离与点的侧面投影到OY W轴的距离相等，都反映点A到H面的距离，即a’a=a"a yw= Aa 。

4〕点的正面投影到OZ轴的距离与点的水平投影到OY H轴的距离相等，都反映点A到W面的距离，即a’a=aa yh= Aa〞。

5〕点的水平投影到OX轴的距离与点的侧面投影到OZ轴的距相等，都反映点A到V面的距离，即aa=a〞a=Aa’。

3 三面投影体系

3 三面投影体系

a
A
X
O
点A的水平投影
H
a
点的二面投影图是将空间点向二个投影面作正投影 后，将二个投影面展开在同一个面后得到的。
两面投影图的画法 V a A V a
X
ax a
O
X
ax
O
H H
a
H
展开时，规定V面不动，H面向下旋转90。用投影图 来表示空间点，其实质是在同一平面上用点在二个不同 投影面上的投影来表示点的空间位置。
1、位置关系
• 以主视图为准，俯视 图在它的正下方，左 视图在它的正右侧，
位置固定，不必标注。
2、三视图之间的“三等”关 系
• 主、俯视图长对正。
• 主、左视图高平齐。
• 俯、左视图宽相等。
2.1.3 两点的相对位置和重影 点
1.两点的相对位置
2.重影点
两点的相对位置
两点的相对位置指两 点在空间的上下、前后、 左右位置关系。
Y
① aa ⊥OX轴 aaz = aaY = XA（A到W面的距离） ② aa⊥OZ轴 aax =aa Y = ZA （ A到H面的距离）
③aax= aaz= YA
（A到V面的距离）
??已知点的两个投影，求第三投影。
解法一:
a● ax az
●
a
通过作45°线 使aaz=aax
a● 解法二:
Bb
O
a
b
Cc c
Aa
例题3：根据投影图判断点在空间的位置
b'
V
B
X a' b c' c O C
a A
例题4：画出点（15，5，10）的三面投影及空间位置
a'

点、线、面的三面投影

点、线、面的三面投影

0 2 （3）直角投影定理
两直线在空间上垂直（垂直相交或垂直交叉），当其中一条直 线平行于某一投影面时，则两直线在该投影面上的投影垂直。 利用直角投影原理，可完成过点作投影面平行的垂线，或与其 相关的求点到直线距离，求直角三角形、等腰三角形等平面图形投 影的作图问题。
0 2
0 4）曲线投影 2 （1）曲线的形成和分类
②三个投影的长度都小于实长。
事实上，只要空间直线的任意两个投影都呈倾斜状态，则该直线
一定是一条一般位置直线。
0 2）直线上点的投影特性 2
（1）从属性 （2）定比性 点在直线上，点的投影在直线的同面投影上。 点分线段之比等于点的投影分线段的投影之比。
0 2
例 题：
0 3）空间两直线的相对位置 2
0 2 （ 3）常见曲线的投影
·当圆所在的平面为投影面垂直面时， 圆在所垂直的投影面的投影为直线，线 段的长度等于其直径。在另一投影面上 的投影则为椭圆。
·当圆所在平面为一般位置平面时，
圆的两个投影均为椭圆。
0 2
②圆柱螺旋线的投影 一动点在正圆柱表面上绕其轴线作等速回转运动，同时沿 圆柱的轴线方向作等速直线运动，则动点在圆柱表面上的轨迹 称为圆柱螺旋线。常见实例为螺旋楼梯、弧形楼梯
正面投影反映实长及倾角，水平投影及侧面投影垂直于OY轴
0 2
侧平线——平行于W面，同时倾斜于H、V面的直线。
侧面投影反映实长及倾角，水平投影及正面投影垂直于OX轴
0 投影面平行线的投影特性可概括如下： 2
面的倾角。
①直线在它所平行的投影面上的投影反映实长，且倾斜于投
影轴，该投影与相应投影轴之间的夹角，反映直线与另两个投影 ②该直线在其他两个投影面上的投影分别平行于相应的投影 轴，且小于实长。 事实上，在直线的三面投影中，若有两面投影垂直于同一投 影轴，而另一投影处于倾斜状态，则该直线必平行于倾斜投影所 在的投影面，且反映与其他两投影面夹角的实形。

画法几何与机械制图立体的投影21立体及其表面上的点与线立体的三面投影三视图

画法几何与机械制图立体的投影21立体及其表面上的点与线立体的三面投影三视图

S
⑴ 棱锥的组成
由一个底面和若干
侧棱面组成。侧棱线交 于有限远的一点——锥
A
C
s
顶。
B
s
⑵ 棱锥的三视图
⑶时，在棱其锥棱底处锥面于面AB图上C是示取水位点平置
面，同在样俯采视用图平上面反上映取实 点形法。。侧棱面SAC为侧垂
a a
k n
b s kn
k (n) c a(c) b c
面，另两个侧棱面为一
1(2)
a3(4)
O A
O1 A1 1″ 3″ a
2″ 4″
利用投影 的积聚性
2.圆锥体
⑴ 圆锥体的组成
由圆锥面和底面组成。
⑵ 圆圆锥锥体面的是三由视直线图SA ⑶绕转而与轮在成它廓图。相线示交素位的置线轴，的线俯投OO视1影旋图与
s
●
为 腰称三一为曲角圆母S面称形。线的为，另。锥可三两圆顶角个见锥，形视性面直的图上的线底为过判S边等锥A断
CDE的正面投影，求作侧面和水平投影。
分析：
a' b'
AB是圆柱体上的素线 （直线）；
(e')c'
e"
c" BC一部分是前半圆柱
d'
d"
面上的曲线，另一部分
是前半圆弧回转面上的
曲线；
水平和正面投 CDE是圆弧回转面上纬
影是全等的图 圆的一段。
形。
曲面立体
相切处无线
作业： P9 : 1~5 P10：1、3、4、6、7
影，四点在这个纬圆上，其 投影必定在纬圆的投影上。
1）正面投影中过 e' 作一 个纬圆投影（积聚为一过 e' 的水平直线）。

立体上点的三面投影

立体上点的三面投影
线面分析法
对于难以用形体分析法简化的复杂立体图形，可以采用线面 分析法。即根据立体图形上的线、面的性质，分析它们在三 面投影中的形状和位置关系，从而画出立体图形的三面投影 。
2023
PART 04
三面投影在工程设计中的 应用
REPORTING
机械零件图表示方法
正投影法
将物体放在三个投影面之间，通过正投影的方式得到物体的三面视图，即主视图 、俯视图和左视图。这种方法能够准确地表达物体的形状和大小，适用于复杂的 机械零件。
环境因素
如温度、湿度、光照条件 等。
人为因素
操作不规范、观测不准确 等。
提高精度和降低误差策略探讨
选用高精度仪器
采用更高精度的投影仪和 测量设备。
严格控制环境因素
保持恒定的室内温度和湿 度，提供稳定的光照条件。
规范操作流程
制定详细的操作规范，确 保每一步操作的准确性和 可重复性。
优化设计思路和方法分享
正方体在三个投影面 上的投影形状均为正 方形。
典型案例分析讨论
案例二：圆柱体投影分析 圆柱体在水平投影面上的投影为圆形，而在正面和侧面投影面上的投影为矩形。
通过测量圆形和矩形的尺寸，可以推算出圆柱体的实际尺寸和形状。
典型案例分析讨论
01
案例三：球体投影分析
02
球体在三个投影面上的投影均为圆形。
通过测量三个圆形的大小和位置关系，可以推算出球体的实际
2023
PART 03
立体图形三面投影方法
REPORTING
基本立体图形三面投影
棱柱的三面投影
棱柱的顶面和底面平行于投影面 时，其投影为矩形或正方形；侧
面投影为平行线或斜线。
棱锥的三面投影

三视图投影性质及画法

三视图投影性质及画法

(一) 回转体的形成方法
名称 圆 锥 体
圆柱体
圆球体
圆环体
回 转 面 形 成
直母线绕和 它相交的轴线回 转而成圆锥面
O S
直母线绕和 它平行的轴线回 转而成圆柱面
O
A
圆母线绕以 它的直径为轴线 回转而成圆球面
O
圆母线绕和 它的共面但不过 圆心的轴线回转 而成圆环面
O
方
法
和
简
图
A
O
A1 O
O
O
形体 由圆锥面和一个圆 由圆柱面和两个圆 由圆球面围成的 由圆环面围成的
o'
o”
o
以底面对称中心作为坐标原点
二、平面立体及其表面上的点和线
(三) 平面立体的画法
棱线的可见投影画成粗实线，棱线的不可见投影画成细虚线。
注意：
s'
s”
1.所有投影的边缘轮 廓线都是可见的，要用粗 实线画出。
a'
1' c' 2'
2.边缘轮廓线内直线
c
b' s
的可见性，要利用交叉两
1(2)
直线上的重影点来判断。 a
各点投影符合 三面投影特性
俯视图：从上向下做正投射得到的图形。 左视图：从左向右做正投射得到的图形。
§7-1 立体及其表面上的点和线
一、立体的三视图及其投影规律
(一) 三棱锥的三视图
Z
V
s'
s”
a' b'
c'
a”
X
O (c”)
a
sc
b
b” Y
投影过程： (1)建立坐标系; (2)作正投影; (3)投影面展开;

4-1完成下列立体及其表面上的各点三面投影.ppt

4-1完成下列立体及其表面上的各点三面投影.ppt

I淮海工学院
1. 补全水平投影，求作侧面投影。
1.补全水平投影，求作侧面投影
I淮海工学院
I淮海工学院
2.作第三投影
2. 求作第三投影。
I淮海工学院
I淮海工学院
4-3平面立体的截交线（二）
11..作 作出出正正五棱五柱楞截柱切后截的切侧面后投的影侧。 面投影
I淮海工学院
2.2.作作出出带有带矩有形矩穿形孔的穿三孔棱的柱的三侧楞面柱投影的。侧面投影
I淮海工学院
4.求作水平投影。 4. 求作水平投影。
I淮海工学院
4. 求作水平投影。
I淮海工学院
4-7立体的相贯线（一）
1.1补.全补侧全面投侧影。面投影。
I淮海工学院
2.补全水平投影
2. 补全水平投影。
I淮海工学院
3.补全正面投影
3. 补全正面投影。
I淮海工学院
4.补全水平投影
补全水平投影。
I淮海工学院
I淮海工学院
2. 求作立体的侧面投影。
2.求作立体的侧面投影。
I淮海工学院
I淮海工学院
4-5曲面立体截交线（二）
1.完成圆柱被截后的水平投影。
1. 完成圆柱被截后的水平投影。
I淮海工学院
1. 完成圆柱被截后的水平投影。
I淮海工学院
2.完成2. 圆完柱成被圆截柱被后截的后水的平水投平影投。影。
I淮海工学院
2. 完成圆柱被截后的水平投影。
I淮海工学院
3. 求作截交线的水平投影。
3.求作截交线的水平投影。
I淮海工学院
3. 求作截交线的水平投影。
I淮海工学院
4.求作侧4.面求投作影侧。面投影。
I淮海工学院

点的三面投影规律

点的三面投影规律

为表示点的各投影的对应关系用细线相连接。点的投影连线与投影轴的交点分别记做ax、ay、az。
05
如A—水平投影a，正面投影a'，侧面投影a''。
一、点的三面投影
设第一分角内有一A点，过A点分别向三投影面投射即得A点的三面投影。 将三投影面展开便得到 点的三面投影图点的三面投影图如下图所示。
二、点的三面投影与直角坐标的关系 为了研究问题方便，可将三投影面体系视为一空间直角坐标系。这样就可将H、V、W三投影面视为坐标平面，X、Y、Z三投影轴视为坐标轴，投影原点O视为坐标原点。
三、点的三面投影规律 例1.已知点A（30、15、25）求作A点的三面投影。
1.分别在X、Y、Z轴上量取 A点的坐标30、15和25， 得ax、ayh、ayw和az点
2.过ax、ayh、ayw和az 点作A点投影的连线
3.各连线的交点即为所求
作图步骤：
三、点的三面投影规律 例2: 已知B（40、30、0）作出B点的三面投影。 问题：根据B点的坐标分析B点的位置。 因B点的坐标（40、30、0）中Z坐标为0，故B点位于H面上。
引入坐标系的概念后，就可用坐标说明点的位置。
三个有序的坐标即X、Y、Z可确定惟一一个点的位置 点的坐标表示方法：A（X，Y，Z）例如：A（15，20，8）、B（5，30，25）
二、点的三面投影与直角坐标的关系
二、点的三面投影与直角坐标的关系
点的坐标还表示了点到投影面的距离。
XA=a ayh=a ' az=A 点到W面的距离
作图步骤：
1.按点的投影规律作点的投影连线
2.投影连线的交点即为B点的水平投影
判断方法：
四、两点的相对位置
1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(2)判 别: 投影在 H 面上重合时，上者可见(Z 坐标大的可见)； 投影在 W 面上重合时，左者可见(X 坐标大的可见)。
(3)标 注：将在某投影面上 不可见的点 加 括 号 标 注 以 示区别。
请点击鼠标左键显示后面内容
例3. 已知C点距W面5、距V面10、距H面10 mm,
D点距W面15、距V面10、距H面5 mm，求
立体上点的投影 PROJECTION OF PINTS
非机类
一、立体上点的三面投影 二、空间二点的相对位置 三、重影点的判别与标注 四、练习题
深圳大学工程
V
a 点在水平面 H 上的投影；x
a' 点在正平面 V 上的投影；
a " 点 在 侧 平 面 W 上 的 投 影 。
YH
X = a’az = aaYh → A 点 到 侧 平 面 W 的 距 离 ；
Y = aax = a”az → A 点到正平面 V 的 距 离 ；
Z = a’ax = a”aYw → A 点 到 水 平 面 H 的 距 离 。
请点击鼠标左键显示后面内容
例1.已知A点的坐标为（5，10，15）,求其三面投影。
Z
前，后 (在 H，W 面上看坐标差 Y)；
左，右 (在 V，H 面上看坐标差 X)。
V a’ A
Z b’
X
a’’ W
Z
B b’’ Y
x
Y a
H
b
X
Y
请点击鼠标左键显示后面内容
例2.已知B点在A下10,A后5,A左10 mm处,求B点的三投影。
z
a’
a”
下 10
b’
b”
x
左 10
0
A B
Yw
b 后5
请点击鼠标左键显示后面内容
z
A
a’
a’’
15
5
x
0
Yw
10
45
a
作图步骤：
（1）画出坐标原点及各轴;
Yh
请点击鼠标左键显示后面内容
（2）根据A点的坐标求其V、H面的投影 a’,a;
（3）根据点的投影规律求出第三投影 a”。
二.空间二点的相对位置
A与B二点的相对位置: 上 ， 下 (在 V， W 面 上 看 坐 标 差 Z)；
Z
a' A a" W
0
a
Y
H
请点击鼠标左键显示后面内容
一．点的三面投影 Z
2. 点的三面投影规律
V a’
a.a’ 0X (即长对正, X 相等);
az a”
W
Z
a’.a” 0Z (即高平齐, Z 相等); X a.a” 0Y (即宽相等, Y 相等)。
ax
X
0 Y aYw
Y
Y
a
aYh
H
3. 点的坐标与投影的关系
a
作图步骤：
（1）根据B的相对位置求 其V.H面的投影 b’,b;
Y h （2）根据点的投影规律 求其第三投影 b”。
请点击鼠标左键显示后面内容
三．重影点的判别与标注
(1)定义: 当 空 间 二 点 在 某 一 投 影 面 上 的 投 影
重合时，称为该投影面的重影点。
投影在 V 面上重合时，前者可见(Y 坐标大的可见)；
(2)
a’ b’
a’’ b’’
c’
c’’
a’ b’ c’
a’’ b’’(c’’)
b a(c )
abc
请点击解答显示其内容
C、D二点的三面投影,并判别其可见性。
z
A
a’
a”
c’
c”
( b ’)d’
10
b” d”
x
5
50
B
C
D Yw
15
10
10
b
d
a（C）
作图步骤：
1.求C点的三投影 c,c’,c”;
Y h 2.求D点的三投影 d,d ’,d ”
请点击鼠标左键显示后面内容
练习题：已知各点的两个投影，求其第三投影。
(1)