第三章-点、线、面的投影(1)知识讲解
- 格式:ppt
- 大小:1.24 MB
- 文档页数:61





Fundamentals of Engineering Graphics第三章点、线、面、体的投影(1)第三章点、线、面、体的投影(1)§3.1 点的投影规律P3~22Projection of Points§3.2 线的投影规律P23~72Projection of lines§3.3 面的投影规律P73~128Projection of Planes3a-A 点的水平投影(H 面投影)a’-A 点的正面投影(V 面投影)HVOXA WY Za”-A 点的侧面投影(W 面投影)二、点A 在三投影体系中的投影注:在标记时,空间点用大写字母表示,点的投影用小写字母表示。
a a’a”一、三投影面体系中的点A 点为三面投影体系中的点§3.1点的投影规律过空间A 点分别向三个投影面作射线,得交点分别为a 、a’、a”。
W VH●●●●XYZOVHWAaa "a 'xa a za y向右翻向下翻不动三、A 点三面投影的展开a a Za a 'ya ya XYY O"●●a z●x●●●●XYZOVHWAaa "a '①a 'a ⊥OX 轴②aa x = a "a z =y=A 到V 面的距离a 'a x = a "a y =z=A 到H 面的距离aa y = a 'a z =x=A 到W 面的距离xa a za y●●YZa za "XYa yOaa xa ya '●a 'a "⊥OZ 轴四、点在三投影面体系中的投影规律五、点的三面投影和坐标的关系yxzOA VHWa'a a"XZ Y水平投影a 反映了A 点的X 、Y 坐标;(x, y )(x, z )(y, z )正面投影a’反映了A 点的X 、Z 坐标;侧面投影a”反映了A 点的Y 、Z 坐标。



点线面的投影投影是几何学中一个重要的概念,用来描述物体在不同维度中的影子或映像。
在三维空间中,投影通常分为点投影、线投影和面投影三种形式。
本文将对点线面的投影进行讨论,并探索其在现实生活中的应用。
一、点的投影点的投影是指当一个点在一个平面上投影时,与该点连线垂直于平面的投影点。
这个投影点可以将原始点的位置在平面上进行准确表示,而不会改变该点的其他性质,如颜色、大小等。
在现实生活中,点的投影有着广泛的应用。
例如,在建筑设计中,建筑师需要通过对建筑物顶部的点进行投影来确定其在平面图上的位置。
同样,在地图制作中,将地球上各个城市的经纬度进行投影来绘制平面地图也是常见的应用。
二、线的投影线的投影是指当一条线在三维空间中投影到一个平面上时,将线段两个端点对应连接起来的线段。
线的投影可以更直观地展示出线在平面上的位置和方向。
线的投影在工程和制图中有着广泛的应用。
例如,在建筑设计中,工程师可以通过将建筑物的立面进行投影,来更好地展示建筑物的外观和形状。
此外,在工程测量中,通过线的投影可以准确地测量出建筑物内部的各种线段长度和角度,为工程施工提供了重要的参考。
三、面的投影面的投影是指当一个平面在三维空间中投影到另一个平面上时,将原始平面的各个顶点在投影平面上对应连接起来的多边形。
面的投影能够完整地展示出原始平面的形状和大小。
面的投影在几何学和地理学中都有着广泛的应用。
例如,在地图投影中,通过将地球表面的多个面投影到一个平面上,可以制作出我们常见的地图样式。
此外,在几何学研究中,通过面的投影可以确定不同形状的二维图形,为解决问题提供了重要的思路。
总结起来,点线面的投影是几何学中重要的概念,用来描述物体在不同维度下的影子或映像。
它们在建筑设计、地图制作、工程测量等领域都有着重要的应用。
通过理解和应用投影,我们可以更好地理解和展示物体的形状、位置和方向,为解决实际问题提供了有力的工具。
以上是对点线面的投影的简要介绍,希望能够帮助您更好地理解和应用投影的概念。
投影中心【组织教学】清点人数,填写教学日志 【复习导入】1、平面图形的尺寸及形状分析的步骤。
2、平面图形的画图方法及作图步骤。
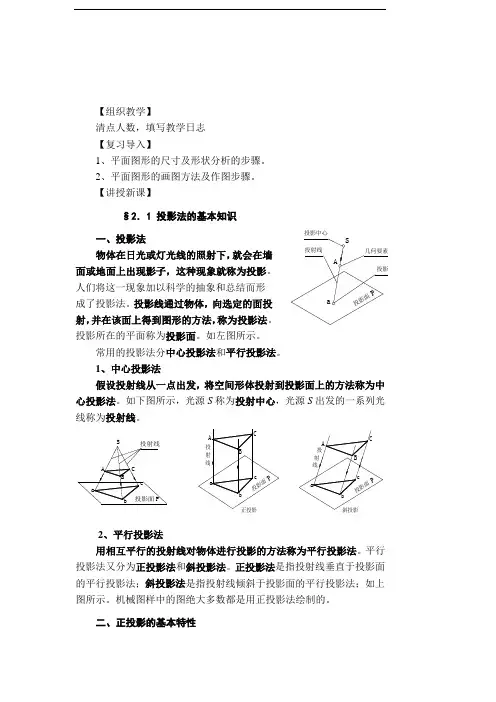
【讲授新课】§2.1 投影法的基本知识 一、投影法物体在日光或灯光线的照射下,就会在墙面或地面上出现影子,这种现象就称为投影。
人们将这一现象加以科学的抽象和总结而形成了投影法。
投影线通过物体,向选定的面投射,并在该面上得到图形的方法,称为投影法。
投影所在的平面称为投影面。
如左图所示。
常用的投影法分中心投影法和平行投影法。
1、中心投影法 假设投射线从一点出发,将空间形体投射到投影面上的方法称为中心投影法。
如下图所示,光源S 称为投射中心,光源S 出发的一系列光线称为投射线。
2、平行投影法用相互平行的投射线对物体进行投影的方法称为平行投影法。
平行投影法又分为正投影法和斜投影法。
正投影法是指投射线垂直于投影面的平行投影法;斜投影法是指投射线倾斜于投影面的平行投影法;如上图所示。
机械图样中的图绝大多数都是用正投影法绘制的。
二、正投影的基本特性1、类似性(又称为收缩性)当直线、曲线或平面倾斜于投影面时,直线或曲线的投影仍为直线或曲线,但小于实长,平面的投影仍为平面,与真实图形类似,但小于真实图形的大小。
2、真实性当直线、曲线或平面平行于投影面时,其投影反映原线段的实长或平面图形的真实形状。
3、积聚性当直线、平面或曲面垂直于投影面时,直线的投影积聚成点,平面的投影积聚成直线,曲面的投影积聚成曲线。
§2.2三视图一、三视图的形成1、三面投影体系的建立根据物体的一个投影图是不能全面地表达出其空间形状和大小的。
因此我们建立一个由三个互相垂直的平面组成的投影体系来表达物体的形状,这个投影体系称三面投影体系,如下图所示,其中水平放置的平面称为水平投影面用H 表示,简称为H 面;正对着观察者的平面称为正立投影面用V 示,简称为V 面;在观察者右侧的平面称为侧立投影面用W 表示,简称为W 面。

点线面的投影在几何学中,点线面是我们经常遇到的三个基本几何概念。
而投影,则是描述物体在投影面上的呈现方式。
本文将介绍点线面的投影及其相关概念和应用。
一、点的投影点是最基本的几何元素,其在投影面上的投影通常是一个点。
在投影过程中,我们需要考虑点与投影面的垂直关系。
根据垂直关系的不同,点的投影可以分为垂直投影和斜投影两种情况。
1. 垂直投影垂直投影是指点在投影面上的投影与点所在位置之间存在垂直关系。
在垂直投影中,投影点与原点的连线垂直于投影面。
这种情况下,投影点的坐标与原点的坐标在投影面上是一致的。
2. 斜投影斜投影是指点在投影面上的投影与点所在位置之间不存在垂直关系。
在斜投影中,投影点的坐标与原点的坐标在投影面上不一致。
具体来说,斜投影是点与投影面之间的投影线与垂直于投影面的引线所形成的夹角所决定的。
二、线的投影线是由无数个点组成的,其投影与点的投影有所不同。
线在投影面上的投影通常是一条直线,它与原线有着一定的几何关系。
1. 平行投影平行投影是指线在投影面上的投影与原线平行。
在平行投影中,线的投影长度与原线长度相等,而投影点之间的距离也与原线上的点之间的距离相等。
这种投影方式常用于工程制图中,如建筑设计。
2. 失真投影失真投影是指线在投影过程中,投影点之间的距离不等于原线上的点之间的距离。
这种投影方式常见于透视画法中,利用透视原理可以将三维物体在二维平面上进行投影。
三、面的投影面是由无数个点和线组成的,其投影与点和线的投影也有所不同。
面在投影面上的投影通常是一个面,其形状与原面保持一致,但大小和位置可能发生变化。
1. 正投影正投影是指面在投影面上的投影与原面相似。
投影面与原面平行时,正投影的投影面积与原面积相等。
这种投影方式常用于平面图形的绘制中。
2. 斜投影斜投影是指面在投影面上的投影与原面不相似。
投影面与原面不平行时,斜投影的投影面积与原面积不相等。
这种投影方式常用于建筑学和工程学中,用于描述三维物体在二维平面上的投影效果。

中考重点点线面的投影中考重点:点线面的投影1. 点的投影在几何学中,点的投影是指将一个点在平面上投影到另一个平面上形成的图形。
点的投影一般分为垂直投影和斜投影。
垂直投影:当一个点在平面上投影到垂直平面上时,投影点位于垂直平面上的垂直线上,且与原点距离相等。
例如,当一个点A位于平面上,投影面为垂直平面BCD时,投影点B位于垂直线AE上,并且线段AB与点A的距离相等。
斜投影:当一个点在平面上投影到斜面上时,投影点位于斜面上的投影线上,且投影线段的长度与点A到斜面的距离成比例。
例如,当一个点A位于平面上,投影面为斜面BCD时,投影点B位于线段AE 上,并且线段AB与线段AE的长度比等于AB与点A的距离与两个平行面的距离之比。
2. 线的投影线的投影是指将一个线段在一个平面上投影到另一个平面上形成的图形。
线的投影一般分为垂直投影和斜投影。
垂直投影:当一个线段在平面上投影到垂直平面上时,投影线段与原线段平行,并且长度相等。
例如,当线段AB在平面上投影到垂直平面BCD上时,投影线段A'B'与线段AB平行且长度相等。
斜投影:当一个线段在平面上投影到斜面上时,投影线段位于斜面上的投影面上,并且投影线段的长度与原线段长度成比例。
例如,当线段AB在平面上投影到斜面BCD上时,投影线段A'B'位于斜面上的投影面上,并且线段A'B'的长度与线段AB的长度成比例。
3. 面的投影面的投影是指将一个面在一个平面上投影到另一个平面上形成的图形。
面的投影一般分为垂直投影和斜投影。
垂直投影:当一个面在平面上垂直投影时,投影面与原面平行,并且形状相同。
例如,当一个正方体面在平面上垂直投影时,投影形状为相同的正方形。
斜投影:当一个面在平面上斜投影时,投影面与原面不平行,并且形状不同。
例如,当一个正方体面在平面上斜投影时,投影形状为一个菱形。
总结:点线面的投影在几何学中是一个非常重要的概念,它们在平面几何和空间几何中有着广泛的应用。
投影是几何学中一个重要的概念,用于描述一个物体在一个平面上的影子或视图。
在几何学中,我们经常遇到三种常见的几何体:点、线、面。
那么,点、线、面在不同的投影方式下会有怎么样的变化呢?让我们一起来探索一下。
首先,我们来看点的投影。
点是没有维度的几何体,它被认为是零维的,因此点的投影是一个非常简单的概念。
当我们将一个点投影到一个平面上时,投影点的位置与原点重合,这是因为点没有长度、宽度和高度,所以它的影子也只是一个简单的点。
例如,当太阳光照射在地面上时,太阳光的每个光点会在地面上形成一个点的投影。
接下来,我们来看线的投影。
线是一个一维的几何体,它具有长度但没有宽度和高度。
当我们将一条线投影到一个平面上时,投影线是线在平面上的投影,它的长度与线的长度相同,但没有宽度。
换句话说,投影线是线的延长在平面上的一部分。
例如,当我们在地面上放置一根杆子,它的投影线将呈现为一条直线。
最后,我们来看面的投影。
面是一个二维的几何体,具有长度和宽度,但没有厚度。
当我们将一个面投影到一个平面上时,投影是面在平面上的二维投影。
这意味着投影保留了原来面的形状和尺寸,但没有了厚度。
例如,当我们将一个正方形铝箔放在地面上,它的投影将是一个正方形。
投影还可以是其他多边形,如三角形或长方形,取决于面的形状。
综上所述,点、线、面的投影在几何学中有不同的定义和特征。
点的投影只是一个简单的点,线的投影是线在平面上的延长,面的投影保留了面的形状和尺寸。
这些概念在实际生活中有许多应用,如建筑设计、地图制作、艺术绘画等。
因此,理解点、线、面的投影对于我们理解几何学和空间关系有着重要的意义。
在几何学中,投影是一个令人着迷的概念,它能够帮助我们更好地理解物体的形状和位置。
通过研究点、线、面的投影,我们可以更深入地了解它们的特性和变化,并将这些知识应用到实际问题中。
无论是在数学、物理、工程还是艺术领域,点、线、面的投影都是一个不可或缺的概念,它给我们的世界带来了更多的可能性和创造力。