当前位置：文档之家 › 3-3：直线上点的投影规律.

3-3：直线上点的投影规律.

  • 格式：ppt
  • 大小：1.16 MB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

简述直线上点的投影规律

简述直线上点的投影规律

简述直线上点的投影规律
直线上点的投影规律是指当一个点沿着一条直线移动时，它在垂直于该直线的平面上的投影的变化规律。

这里以一条水平直线作为例子进行说明。

1. 初始位置：当点位于直线上时，它的投影重合于直线上的相应位置。

2. 向上移动：当点沿直线向上移动时，其投影在直线上向上移动，但保持与初始位置的水平距离不变。

3. 向下移动：当点沿直线向下移动时，其投影在直线上向下移动，但同样保持与初始位置的水平距离不变。

4. 垂直投影：无论点在直线上的位置如何变化，其投影始终垂直于直线。

5. 投影长度变化：当点距离直线越远时，其投影在直线上的长度也相应增加。

通过以上规律，我们可以观察到点在直线上的投影变化是与该直线垂
直的平面上的投影。

这种规律在几何学、物理学等领域中都有广泛的应用，例如在光学中的成像原理、建筑设计中的阴影效果等。

直线上点的投影规律为我们理解和应用相关领域提供了基础。

点线面的投影分析

点线面的投影分析
一、点的投影分析
点的投影规律： (1)点的正面投影和水平投影的连线
垂直于OX 轴。即ss’⊥ OX
(2)点的正面投影和侧面投影的连线
垂直于OZ 轴。即s’s” ⊥ OZ (3)点的水平投影到OX轴的距离等于
侧面投影到OZ 的距离。
退出 节目录
§2－3 立体表面上点、线、面的投影分析
一、点的投影分析
影面。
退出 节目录
§2－3 立体表面上点、线、面的投影分析
三、平面的投影分析
1.一般位置平面 投影特性：
(1)三个投影都不 反映平面实形。 (2)三个投影均对 投影轴倾斜。
退出 节目录
§2－3 立体表面上点、线、面的投影分析 三、平面的投影分析
2.投影面平行面 投影特性：
（1）在所平行 的投影面上投 影反映实形。 （2）其他两个 投影面上的投 影积聚为直线， 且分别平行于 相应的投影轴。
2.投影面平行面 投影特性：
（1）在所平行 的投影面上投 影反映实形。 （2）其他两个 投影面上的投 影积聚为直线， 且分别平行于 相应的投影轴。
平行于侧面的平面称为侧平面
退出 节目录
§2－3 立体表面上点、线、面的投影分析 三、平面的投影分析
3.投影面垂直面 投影特性：
(1)在所垂直的投 影面内投影积聚 为一段斜线。 (2)其他两个投影 面上的投影均为 缩小的类似形。
平行于侧面的直线称为侧平线
退出 节目录
§2－3 立体表面上点、线、面的投影分析
二、直线的投影分析
3.投影面垂直线 投影特性：
（1）在所垂直的 投影面上投影积 聚为一点。
（2）其他两个投 影面上的投影反 映实长，且分别 垂直于相应的投 影轴。
垂直于水平面的直线称为铅垂线

机械制图-点、直线、平面的投影

机械制图-点、直线、平面的投影
特殊位置点的应用
在机械制图中，特殊位置点常用于 确定物体的形状和大小，如交点、 切点等。
03 直线投影
直线在三投影面体系中的投影
正投影
直线在正投影面上的投影 与原直线平行或重合，且 长度不变。
侧投影
直线在侧投影面上的投影 与原直线垂直，且高度不 变。
水平投影
直线在水平投影面上的投 影与原直线平行，且长度 不变。
直线上的点的投影特性
点在直线上
点的投影在直线的投影上，且与 原点在同一平面内。
点在直线外
点的投影在直线的投影外，且与 原点不在同一平面内。Leabharlann 两直线的相对位置与投影特性
平行线
两直线在正投影面上的投影平行， 且高度相等。
交叉线
两直线在正投影面上的投影相交， 且高度相等。
垂直线
两直线在正投影面上的投影垂直， 且高度相等。
机械制图-点、直线、平面的投影
目 录
• 引言 • 点投影 • 直线投影 • 平面投影 • 实际应用与案例分析 • 总结与展望
01 引言
主题简介
01
机械制图是工程领域中用于表达 和交流设计思想的一种语言，而 点、直线和平面的投影是机械制 图的基础。
02
本主题将介绍点、直线和平面在 机械制图中的投影原理和方法， 帮助读者更好地理解和应用机械 制图。
投影法概述
投影法是将三维物体转换为二维图形 的方法，是机械制图中的基本技术。
投影法分为中心投影法和平行投影法 ，其中平行投影法又分为正投影法和 斜投影法。
02 点投影
点在三投影面体系中的投影
点的三面投影
一个点在三投影面体系中分别在H面、 V面和W面上投下影子，形成三个投 影点。

直线的投影知识

直线的投影知识
图4-28 一般位置直线
1.2 直线上点的投影特性
1. 从属性
直线上点的投影必在该直线的同面投影上，该特性称为点的从 属性。如图4-29所示，C点在直线AB上，根据点在直线上投影的从 属性和点的三面投影规律，可知C点的三面投影c、c′、c″分别在直线 的同面投影ab、a′b′、a″b″上，并且三面投影符合点的投影规律。
1.1 空间各种位置直线的投影特性
1.1 空间各种位置直线的投影特性
投影面垂直线的投影共性为： 直线在所垂直的投影面上的投影积 聚为一点，其他两投影反映实长， 且垂直于相应的两投影轴。
1.1 空间各种位置直线的投影特性
3. 一般位置直线
一般位置直线与三个投影面都倾斜，因此在三个投影 面上的投影都不反映实长，投影与投影轴之间的夹角也不 反映直线与投影面之间的夹角，如图4-28所示。
图4-31 两直线平行
1.3 两直线的相对位置
2. 两直线相交
空间中的两条直线如果相交，则它们的同面投影都相交， 并且交点符合点的投影规律。如果两直线有一个投影面的投影 不相交，则空间的两直线不是相交关系，如图4-32所示。
图4-32 两直线相交
1.3 两直线的相对位置
3. 两直线交叉
空间中两条直线如果交叉，则它们的同面投影既不相交 又不平行，如图4-33所示。
1.1 空间各种位置直线的投影特性
1. 投影面平行线
平行一个投影面，倾斜于另外两个投影面的直线称为投影面平行 线。与H面平行的直线称为水平线，与V面平行的直线称为正平线，与 W面平行的直线称为侧平线。它们的投影特性如表4-1所示。规定直 线与H、V、W面的夹角分别用α、β、γ表示。
1.1 空间各种位置直线的投影特性
1.1 空间各种位置直线的投影特性

点的三面投影规律

点的三面投影规律

为表示点的各投影的对应关系用细线相连接。点的投影连线与投影轴的交点分别记做ax、ay、az。
05
如A—水平投影a，正面投影a'，侧面投影a''。
一、点的三面投影
设第一分角内有一A点，过A点分别向三投影面投射即得A点的三面投影。 将三投影面展开便得到 点的三面投影图点的三面投影图如下图所示。
二、点的三面投影与直角坐标的关系 为了研究问题方便，可将三投影面体系视为一空间直角坐标系。这样就可将H、V、W三投影面视为坐标平面，X、Y、Z三投影轴视为坐标轴，投影原点O视为坐标原点。
三、点的三面投影规律 例1.已知点A（30、15、25）求作A点的三面投影。
1.分别在X、Y、Z轴上量取 A点的坐标30、15和25， 得ax、ayh、ayw和az点
2.过ax、ayh、ayw和az 点作A点投影的连线
3.各连线的交点即为所求
作图步骤：
三、点的三面投影规律 例2: 已知B（40、30、0）作出B点的三面投影。 问题：根据B点的坐标分析B点的位置。 因B点的坐标（40、30、0）中Z坐标为0，故B点位于H面上。
引入坐标系的概念后，就可用坐标说明点的位置。
三个有序的坐标即X、Y、Z可确定惟一一个点的位置 点的坐标表示方法：A（X，Y，Z）例如：A（15，20，8）、B（5，30，25）
二、点的三面投影与直角坐标的关系
二、点的三面投影与直角坐标的关系
点的坐标还表示了点到投影面的距离。
XA=a ayh=a ' az=A 点到W面的距离
作图步骤：
1.按点的投影规律作点的投影连线
2.投影连线的交点即为B点的水平投影
判断方法：
四、两点的相对位置
1

第三章点、直线及平面的投影详解

第三章点、直线及平面的投影详解
第三章 点、直线及平面投影
§3－1 点的投影 §3－2 直线的投影 §3－3 平面的投影
点线面的投影规律
通过上一节的学习及画图实践，可以体会到 画一个物体的三视图，实质上是画出组成物体的 各个面的投影，而各个面是由棱线围成的，各棱 线是由两个端点决定的。
因此，为了迅速而正确地画出物体的视图， 还需研究构成物体的基本几何元素点、线、面的 投影。
Y
H
向下翻
●a
O
W
ay
Y
a ●
X ax
a●
点的投影规律
Z az
a
●
Z
V a
●
az
O
Y
ay
A
X ax
●
●a
O
W
ay
Y
a●
ay
H
Y
① aa⊥OX轴
aa⊥OZ轴
连影垂轴
② aax= aaz= y = A 到 V 面的距离 aax= aay= z = A 到 H 面的距离 aay= aaz= x = A 到 W 面的距离
Z
X
V a′ A
a″ W
a b
a
Z a
b
O
YW
b′
B b″
b
判断方法：
YH
x
ab
H
Y
x 坐标大的在左 y 坐标大的在前
z 坐标大的在上
例2.已知B点在A下10，A后5，A左10 mm处，求B点的三投影。 作图步骤：（1）根据B的相对位置求 其V.H面的投影 b’,b;
（2）根据点的投影规律,求其第三投影 b”。
§3－1 点的投影
一、点在一个投影面上的投影
P

直线上的点与线投影

直线上的点与线投影

真长（TL)
坐标差 △Z、△Y、△X
α、β、γ
H、V、W投影长
直角三角形法
B
α A
b a
ZA
ZB-ZA
ZB
b'
ZB-ZA
a'
X
o
b
a
α
ZB-ZA
1、求直线的实长及对水平投影面的夹角角
|zA-zB|
AB
ab
|zA-zB|
AB
|zA-zB|
ab O
|zA-zB |
AB
2、求直线的实长及对正面投影面的夹角
c
zA-zB
ab
c
§3.5 两直线的相对位置
两直线平行
空间两直线的相对位置
两直线相交
两直线交错（相交、交叉）
空间两直线平行
两直线在空间互相平行，则它们的同面投影也相互 平行。反之，若两直线的各个同面投影均相互平行，则 该两直线在空间也一定相互平行。
b' B d'
a'
D
a'
c'
X
A
C
OX
bd
acaຫໍສະໝຸດ b'影引垂线，较高的一点看得
n'
见，较低的一点则看不见。 c'
O
（2）判别V面重影点的可见
性，必须从V面投影向H面投
m(n)
e
b
影引垂线，较前的一点看得
c a
见，较后的一点则看不见。
f
d
直角的投影
两条互相垂直的直线，若其中有一条 是某一投影面的平行线，则它们在该投影 面的投影必互相垂直。
直角的投影
b' d'

工程制图与识图3-3：直线上点的投影规律

工程制图与识图3-3：直线上点的投影规律
一直线上的两线段之比，等于其同面投影之比。这一 性质称之点的定比性。
特性1.从属性
• 点在直线（或平面）上，则该点的投影一定在直线（或平面）的同面投影
上
K在DE上
N在∆ABC上
投影后，k 在ed上
投影后，n在∆ abc上
特性2.定比性
点分线段之比，投影后该比值保持不变； 空间平行的两线段长度之比，投影后该比值不变
根据2：点的投影必在该直线
的同名投影上.
b'
b"
c’
c’’
a'
a"
X
YW
O
经典例题
a
cb
【例3-4】已知直线AB的两面投影，C点在AB上，且已知正面投影点c′,完成直线 和点的三面投影。
作图步骤：求出点A、B的侧面投影a″、b″并连线完成直线的三面投影。 因为C点投影应该符合点的投影规律，故过c′作横线和竖线辅助线； 因为从属性，点C的投影必在直线AB的同名投影上，故所作辅助线与ab、 a″b″的交点即为c、c″。
例 已知直线EF的两面投影及EF上一点C的正面 投影，求点C的水平投影。• 可利用定比性求
e'e' c'c' f'f'
ff
f0
ee
c0
e' c' f'
f
c
f0
c0
小结与作业
• 可选作业： • 《工程制图与识图习题集》 • P20：3-3
点、直线是作图基础
第第3章几何要素投影33直线上点的投影规律及作图方法点直线的投影是制图基础如果点在直线上则点的三面投影就必定在直线的三面投影之上
第3章 几何要素投影

1、投影法

1、投影法
W
定物体的空间形状。
V
Y
需要用平面图形表达
X H
图2
物体空间结构形状
对于复杂物体必须采用多面正投影图才能表达物体的空
间形状，工程上普遍采用三面正投影图，简称三视图。
物体空间投影情况
物体的三视图
2、直角三面投影体系的建立
直角三面投影体系由三个相互垂直的投影面组成 正立的投影面称为正面，用V表示 水平的投影面称为水平面，用H表示 侧立的投影面称为侧面，用W表示
X
b c a
四、两直线的相对位置
1、两直线平行
空间中平行两直线，其同面投影 亦相互平行；
若两直线同面投影相互平行，则 空间中两直线平行
2、两直线相交
空间中相交两直线，其同面投影亦
若两直线同面投影相交，且交点满 足点的投影规律【三等关系】，则
相交；且投影交点是空间交点的投
影（即满足点的投影规律【三等关 系】）。
投影中的几个术语
投影的分类
中心投影法
平行投影法——
投影线相互平行
斜投影
投影方向与投影面倾斜
正投影
投影方向与投影面垂直
二、正投影的基本特征
1、点的正投影特征
在投影面和空间点确定的情况下，点的投影唯一。 然而，在投影面和点的投影确定的情况下，空间点的 位置不唯一
2、直线的正投影特征
积聚性
真实性


(4) 铅垂线
(5) 正平线
(6) 倾斜线
例2 判断左图所示三棱锥中AC、SC、SA直线相对于投影面的位置，
并完成该三棱锥的侧面投影
倾斜线 倾斜线
侧垂线
如何求一般位置直 线的空间实长和对 投影面的倾角？
AB实长

直线投影基本知识

直线投影基本知识

Z
b
Z
b
a
B b
a
b
a
X
O
YW
X
O
b
b A
a
a
Ya
投影特性：1.a b、 a b 、a b 均小于实长 YH
2 、a b、a b 、a b 均倾斜于投影轴 3 、不直接反映直线对投影面的倾角
（2）投影面平行线
水平线—
平行于水平投影面的直线
z
Z
a b
a
b
a
b
A
a
X
O
YW
XB Oba Nhomakorabeaa
b
Y
投影特性: 1． a b =AB
b'
O b
求一般位置直线的实长及其与W面的夹角γ
Z V
b'
B b"
a'
γ
W
X
X O
A
b
a
H
a" Y
X
Z b' b"
实长 γ
a' X
X
a"
O
YW
b
a YH
实长 β
Y a' X
X Z b' b"
γ
实长
a"
O
YW
αb
a
实长 YH
Z
[例] 如图所示, 求直线AB的真长及其对投影面H、V 的倾角α、β。
行，空间两直线就平行。
（2）对于投影面平行线，可采用以下两种方法:
1）若用两个投影判断，其中应包括反映实长的投影。
2）作出投影面平行线的三面投影。
（2）两直线相交

简述直线上的点的投影规律

简述直线上的点的投影规律

简述直线上的点的投影规律
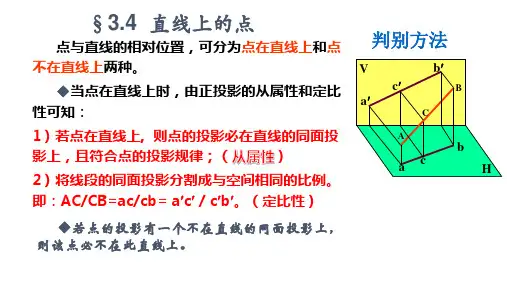
一、点的投影规律：直线上的点在投影过程中遵循以下规律：
1. 点到直线的投影距离是最短的：对于直线上的任意一点P，它到直线上的投影点P'的距离是P到直线距离的最短值。

这是因为直线上的两点之间的距离是最短的。

2. 投影点在直线上：点P'是点P在直线上的投影点，因此它必然在直线上。

这是由于投影是点到直线的垂直距离，而垂直距离只能在直线上得到。

3. 投影点在垂直于直线的线上：直线上的任意一点P'都在直线垂直于直线的线上。

这是由于投影是垂直距离，而垂直距离只能在垂直线上得到。

二、点的投影规律的应用：
1. 几何测量：点的投影规律在几何测量中被广泛应用。

例如，在建筑设计中，可以通过点的投影确定建筑物的阴影位置和大小。

2. 图像处理：点的投影规律在图像处理中也有重要应用。

例如，在
三维渲染中，可以通过点的投影将三维场景投影到二维平面上，以显示给用户。

总结：点的投影规律是直线上的点在投影过程中遵循的规律。

它不仅是几何测量和图像处理中的重要概念，也是理解投影变换的基础。

第3章 直线的投影【画法几何】.

第3章 直线的投影【画法几何】.
1、水平投影ab反映实长， 并反映倾角β 、γ
a


b
2、正面投影a´b´//OX轴， 侧面投影a˝b˝//OYw轴
正平线的投影
c´d´反映CD实长
d′ c′ C


D
d˝ c˝
c˝d˝//OZ轴


c
d
cd //OX轴
d´
d˝ c˝
c´


正平线的投影特 性
1、正面投影c´d´反映实 长，并反映倾角α ,γ
二、 投影面平行线
( 一 ) 含义：仅平行于某一个投影面 的直线，称为投影面平行线。
平行于H面的直线称为水平线 平行于V面的直线称为正平线 平行于W面的直线称为侧平线
水平线的投影
a´b´ //OX轴
a´ A
β
b´ a˝
γ
a˝b˝//OY轴
B
b˝
a
β
γ
b
ab 反映AB的实长
a´
b´
a˝
b˝
(二) 投影面平行线 的投影特性： 水平线
e
f
投影面垂直线的投影特性
1 、 直 线 在 所 垂 直 的 投 影 面 上 积 聚为 一 点 （即有积聚性）
2 、其它两个投影垂直于相应的投影轴，并
且反映实长（即有显实性）。
例3－2：判断AB、CD、DE直线的空间位置，并找出其第三投影
d’ e’
a’ b’ c’
e”
d”
a” c”
b”
正垂线
e
a´
α
b´
B
b´ a´
m
C
b
X
A
O b
α α
a

工程制图 点、直线及平面的投影

工程制图 点、直线及平面的投影

工程制图
B b b
A a
a
a
b
Z
b
a
a
X a
b
O
YW
b
YH
27
工学院 机械系 张文斌
红河学院
从属于V 投影面的铅垂线
工程制图
Z
a
a
b
b
X
O
YW
a(b)
YH
28
工学院 机械系 张文斌
红河学院
从属于OX轴的直线
工程制图
Z
X a
b O
YW
(b)
a
b a(b)
YH
29
工学院 机械系 张文斌
红河学院
二、一般位置直线
(2) 正垂线
(3) 侧垂线
3.从属于投影面的直线
从属于投影面的直线
从属于投影面的铅垂线
从属于投影轴的直线 二、一般位置直线
20
工学院 机械系 张文斌
红河学院 (1) 水平线 — 只平行于水平投影面的直线 工程制图
z
a b
a
b
a
b
A
a
X
O
YW
B
b a
a
b
b YH
投影特性：1．ab OX ; ab OYW
O
YW
b
a(b)
YH
投影特性：1． a b 积聚 成一点
2． a bOX ; a b OYW 3． a b = a b = AB
24
工学院 机械系 张文斌
红河学院 （2）正垂线— 垂直于正面投影面的直线 工程制图
(a)b
(a)b
z a
b
A

现代工程制图总复习

现代工程制图总复习
空间及投影分析： 小圆柱轴线垂直于H面，水平投影积聚为圆，根据相贯线的共有性，相贯线的水平投影积聚在该圆上。大圆柱轴线垂直于W面，侧面投影积聚为圆，相贯线的侧面投影应积聚在该圆上，为两圆柱面共有的一段圆弧。
找特殊点 补充中间点 光滑连接
[例11]补画视图中所缺少的图线。
01
添加标题
[例11]补画视图中所缺少的图线。
的投影面上，集聚为一直线
其他两个面上的投影均为类似形。
投影面平行面
平行于一个投影面，必垂直于另外两个投影面的平面。
投 影 特 性
在它所平行的投影面上的投影反映实形。
另两个投影面上的投影分别积聚成与相应的 投影轴平行的直线。
5、平面上的点和直线
一直线通过平面内的两个点，则此直线必定 在该平面内。
平面立体的截切
求截交线的步骤
☆ 截平面与体的相对位置 截平面与体的几个表面相交
☆ 截平面与投影面的相对位置
确定截交线 的投影特性
确定截交 线的形状
★ 空间及投影分析
★ 画出截交线的投影
分别求出截平面与棱面的交线(或截平面与棱线的交点)的各面投影，并连接成多边形。
注意： 要逐个截平面分析和绘制截交线。当平面体只有局部被截切时，先假想为整体被截切，求出截交线后再取局部。
棱柱的三视图
2.平面基本体
棱柱面上取点
a
a
a
(b)
b
b
棱锥处于图示位置时，其底面ABC是水平面，在俯视图上反映实形。侧棱面SAC为侧垂面，另两个侧棱面为一般位置平面。
s
s
棱锥
棱锥的三视图
b
a
b
c
a(c)
b
s
A
B

工程制图3-3

工程制图3-3

[2] ab∥OYH ；a〞b〞∥OYw ,反映室长
铅垂线
立体三图视
a′
直线投影图
a〞
z a′
C′
a〞 c〞 yw
C′
c〞
A
o
x
b
a[c]
C
a[c] yH
特性：[1]
ac 线积聚成一点
[2] a′c′∥OZ；a〞c〞∥OZ，反映实长
侧垂线
立体三图视
a′ d′
a〞[d〞]
直线投影图
a′ x
d′
z
a〞 [d〞]
S P
主视图投影方向
正垂面的投影特性
z γ α x o YH
主视图投影方向
投影特性：1、正面投影积聚成直线。
2、水平投影和侧面投影为类似性。 3、α、γ为实角。
YW
铅垂面的投影特性
z x β o γ YH
主视图投影方向
投影特性：1、水平投影积聚成直线。
2、正面投影和侧面投影为类似性。 3、β、γ为实角。
A R Q P S P
{
V-----正垂面 H-----铅垂面 W----侧垂面
Q
P
Q
S S
P
A R B
B
主视图投影方向
投影面垂直面的举例
投影面垂直面 : 只垂直于投影面的平面
平面只垂直于 V-----正垂面 H-----铅垂面 W-----侧垂面 蓝色的平面 粉色的平面 黄色的平面 S P Q
{
o a″ b Y
a b =ABcosα a′b′=ABcosβ a″b″=ABcosγ
X
A a H
α
一般位置的直线，对 三个投影面都是倾 斜的。所以一般位 置直线的投影特性 是： 三个投影都是倾斜 直线，并且都小于 实长。

机械制图3直线的投影

机械制图3直线的投影

a
V
＝
A
a'1 V1
＝
＝
V X
ax
H
＝
. ax1
a'1
X
a
H V1 X1
旧投影体系 X —VH
ax
＝
ax1
a
H
X1
新投影体系 X1 —HV1
A点的两个投影：a， a
A点的两个投影：a 1，a
★新投影体系仍然遵守投影的 一般规律：
24
aa 1 X1
a'1ax1 = aax
Gong Zhuorong, Beijing Jiaotong University
“交点”是两直线上的一对重影点，可用于判别其空间位置。
16
Gong Zhuorong, Beijing Jiaotong University
交叉二直线的空间位置的判别
利用前面讲述的重影点进行判别， 到另外两个投 影上去找遮挡关系
1′
c
′
3′(4′)
●
● ●
2′
a′
X a
●4
● ●
c 3 1(2)
换H面行吗？
旧投影到旧轴的距离。
同时求出直线AB的实长及与H面的夹角α。
Of course！
27
Gong Zhuorong, Beijing Jiaotong University
2. 将投影面平行线变换成投影面垂直线
a
XV H
a
b
b
.
H X1 V1
(b'1) a●'1
V1
V
b′
a
B ●(b'1) a′1
投影的长度均比空间线段短，即都 不反映空间线段的实长。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
点、直线的投影是制图基础
工程图是工程语言,是工程技术人员必备技能
《工程制图与识图》（李奉香主编）电子课件 机械工业出版社
3.3 直线上点的投影规律
两个性质
如果点在直线上，则点的三面投影就必定在直线的三 面投影之上。这一性质称之点的从属性。
一直线上的两线段之比，等于其同面投影之比。这一 性质称之点的定比性。
工程图是工程语言,是工程技术人员必备技能
《工程制图与识图》（李奉香主编）电子课件 机械工业出版社
特性1.从属性
• 点在直线（或平面）上，则该点的投影一定在直线（或平面）的同面投影 上
K在DE上
N在∆ABC上
投影后，n在∆ abc上
投影后，k 在ed上
工程图是工程语言,是工程技术人员必备技能
《工程制图与识图》（李奉香主编）电子课件 机械工业出版社
特性2.定比性
点分线段之比，投影后该比值保持不变； 空间平行的两线段长度之比，投影后该比值不变
K在CD上则 CK：KD=ck：kd
工程图是工程语言,是工程技术人员必备技能
《工程制图与识图》（李奉香主编）电子课件 机械工业出版社
• 2)定比性：点的投影将线段的同名投影分割
成相同的定比。
Z
b'
a' c' X
根据1 ：点投影符合点的投影规律；
根据2：点的投影必在该直线
的同名投影上.
b'
b"
c’
c’’
a'
a"
X
YW
O
经典例题
a
c b 工程图是工程语言,是工程技术人员必备技能
《工程制图与识图》（李奉香主编）电子课件 机械工业出版社 【例3-4】已知直线AB的两面投影，C点在AB上，且已知正面投影点c′,完成直线 和点的三面投影。
ac
b
b"
c" a"
点 C 将 线 段 AB 分 割成AC，CBຫໍສະໝຸດ YW 则：AC∶CBO
=ac∶cb
=a’c’∶c’b’
=a’’c’’∶c’’b’’
Y 工程图H是工程语言,是工程技术人员必备技能
直线上点的《投工程影制图作与识图图方》（法李奉香主编）电子课件 机械工业出版社
已知 ：空间点C在直线AB上及C点正面投影，求点C另两面投影。
例 已知直线EF的两面投影及EF上一点C的正面 投影，求点C的水平投影。• 可利用定比性求
e'e' c'c' f'f'
ff
f0
ee
c0
e' c' f'
f
c
f0
c0
工程图是工程语言,是工程技术人员必备技能
设计、制作:李奉香
小结与作业
• 可选作业： • 《工程制图与识图习题集》 • P20：3-3
点、直线是作图基础
《计工算程机制系图统与识应图用》课件
主 编：李奉香 副主编：马爱兵 范忠和 易 敏 参 编：张荣 刘文霞 程志铭 吉丽 宋小军 张海霞
万志华 季学毅 毛兰霞 张南 徐晓玲 主 审：黄向裕
（本章课件由李奉香和吉丽制作）
《工程制图与识图》（李奉香主编）电子课件 机械工业出版社
第3章 几何要素投影
3.3 直线上点的投影规律及作图方法
下一张 返回 退出
作图步骤：求出点A、B的侧面投影a″、b″并连线完成直线的三面投影。 因为C点投影应该符合点的投影规律，故过c′作横线和竖线辅助线； 因为从属性，点C的投影必在直线AB的同名投影上，故所作辅助线与ab、 a″b″的交点即为c、c″。
工程图是工程语言,是工程技术人员必备技能
《工程制图与识图》（李奉香主编）电子课件 机械工业出版社