课时5 平移专题

《平移》教案一、教学目标1.经历观察、分析、操作、欣赏以及抽象、归纳等过程，以及与他人合作交流探索的过程，进一步发展空间观念，增强审美意识，学会用运动的观点分析问题.2.通过实例，认识图形平移，了解平移的特征，理解平移的含义，会进行点的平移.3.理解平移前后两个图形对应点连线平行且相等的性质，能解决简单的平移问题.二、教学重点与难点重点：图形平移的特征和作平移图形.难点：平移的性质探索和理解.三、教学过程（一）创设情境，引入新课1.感受平移，体验新知你坐过公车和搭过电梯吗？它是一种什么样的运动？这样的运动在生活中还有哪些现象？（活动1：学生讨论）2.观察图形，形成印象生活中有许多美丽的图案，他们都有着共同的特点，请同学们欣赏下面图案.观察上面图形，我们发现他们都有一个局部和其他部分重复，如果给你一个局部，你能复制他们吗？学生思考讨论，并回答问题.(1)它们有什么共同的特点？(2)能否根据其中的一部分绘制出整个图案？（活动2：师生交流.）这些美丽的图案是由若干个相同的图案组合而成的，每个图形都有“基本图形”，而“基本图形”是什么？如第一个图形是中间一个正方形，上、下有正立与倒立的正三角形，下排的左图中的“基本图形”是鸽子与橄榄枝；下排右图中的“基本图形”是上、下一对面朝右与面朝左的人头像组成的图案.3.实践探索，得出新知探究：设计一个简单的图案，利用一张半透明的纸附在上面，绘制一排形状，大小完全一样的图案如：引导学生找规律，发现平移特征，回答下面问题：1、图形经过平移后，_______图形的位置，________图形的形状，________图形的大小.(填“改变”或“不改变”)2、经过平移，每一组对应点所连成的线段________.归纳 (活动3：分组讨论)平移：(1)把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同. (2)新图形中的每一点，都是由原图形中的某一个点移动后得到的，这两个点是对应点. (3)连接各组对应的线段平行且相等.图形的这种变换，叫做平移变换，简称平移简单归纳为两点：1.平移的方向. 2.平移的距离四、典例剖析，深化巩固1. 把鱼往左平移8cm.(假设每小格是1cm2)五、小结(学生回答)：这节课你学了什么？知道了什么？学会了什么？六、课后作业必做题：教科书习题：3.6题《平移》习题1、决定平移的基本要素是＿＿＿＿和＿＿＿＿。

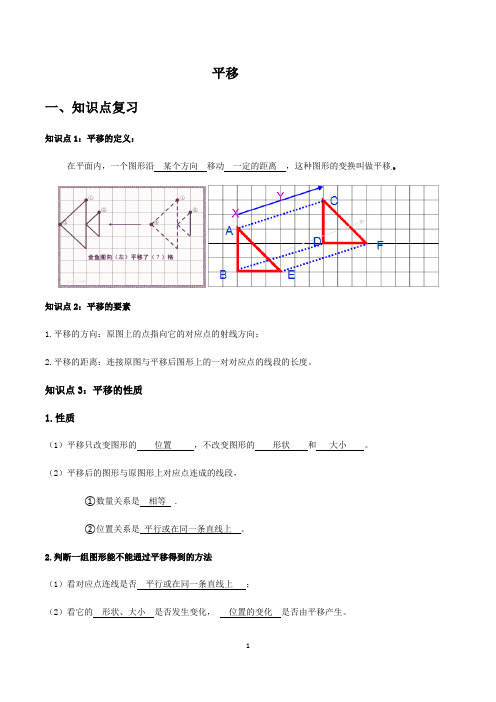
平移一、知识点复习知识点1：平移的定义：在平面内，一个图形沿某个方向移动一定的距离，这种图形的变换叫做平移。

知识点2：平移的要素1.平移的方向：原图上的点指向它的对应点的射线方向；2.平移的距离：连接原图与平移后图形上的一对对应点的线段的长度。

知识点3：平移的性质1.性质（1）平移只改变图形的位置，不改变图形的形状和大小。

（2）平移后的图形与原图形上对应点连成的线段，①数量关系是相等 .②位置关系是平行或在同一条直线上。

2.判断一组图形能不能通过平移得到的方法（1）看对应点连线是否平行或在同一条直线上；（2）看它的形状、大小是否发生变化，位置的变化是否由平移产生。

★★★特别注意：平移是由平移的方向和距离决定的，平移必须指明平移的方向和距离；平移是在平面内，整个图形沿着某一直线平行移动的过程，原图上的每个点都沿同一方向移动相同的距离；平移的距离不能为0；平移的方向是任意的，但就一次平移而言，只能有一个方向，一次平移完成后可以改变方向进行下一次平移。

二、典型例题题型1：生活中平移现象【例题1】（2017春•乌海期末）下列运动属于平移的是（）A．荡秋千 B．推开教室的门 C．风筝在空中随风飘动 D．急刹车时，汽车在地面上的滑动【例题2】：（2016春•淮安期中）下列现象：①电梯的升降运动，②飞机在地面上沿直线滑行，③风车的转动，④冷水加热过程中气泡的上升．其中属于平移的是（）A．①② B．①③ C．②③ D．③④题型2：平移的性质【例题4】：（2016春•沧州期末）在下列说法中：①△ABC在平移过程中，对应线段一定相等；②△ABC 在平移过程中，对应线段一定平行；③△ABC在平移过程中，周长保持不变；④△ABC在平移过程中，对应边中点所连线段的长等于平移的距离；⑤△ABC在平移过程中，面积不变，其中正确的有（）A．①②③④ B．①②③④⑤ C．①②③⑤ D．①③④⑤题型3：与平移有关的计算【例题5】：（2015春•石家庄期末）如图，将△ABC沿射线BC方向移动，使点B移动到点C，得到△DCE，连接AE，若△ABC的面积为2，则△ACE的面积为（）A ．2B ．4C ．8D ．16【例题6】：（2017秋•兴化市期末）如图，将△ABE 向右平移2cm 得到△DCF ，AE 、DC 交于点G ．如果△ABE 的周长是16cm ，那么△ADG 与△CEG 的周长之和是 cm 。

人教版七年级下册数学5.4平移 专题练习一.单选题（共 10 小题）1、如图，△ABC 中，∠ABC=90°沿BC 所在的直线向右平移得到△DEF ，下列结论中不一定成立的是（ ）A ．EC=CFB ．∠DEF=90°C ．AC ＝DFD ．AC ∥DF2、如图是一个基本图形，将其平移四次，把得到的新图形结合起来，能得到的图案是（ ）A ．B ．C ．D ．3、如图，在三角形ABC 中，90,3cm,4cm BAC AB AC ∠=︒==，把三角形ABC 沿着直线BC 向右平移2.5cm 后得到三角形DEF ，连接,AE AD ，有以下结论：①AC DF ∥；②AD CF ∥；③ 2.5cm CF =；④DE AC ⊥．其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个4、如果存在一条线把一个图形分割成两个部分，使其中一个部分沿某个方向平移后能与另一个部分重合，那么我们把这个图形叫做平移重合图形．下列图形中，平移重合图形是( )A ．平行四边形B ．等腰梯形C ．正六边形D ．圆5、如图，将边长为5cm 的等边三角形ABC 沿边BC 向右平移3cm ，得到△DEF ，则四边形ADFB 的周长为（ ）cm ．A ．20B ．21C ．22D ．23 6、如图，面积为12cm 2的△ABC 沿BC 方向平移到△DEF 的位置，平移的距离是边BC 长的2倍，则图中四边形ACED 的面积为（ ）A ．24cm 2B ．36cm 2C ．48cm 2D ．无法确定7、如图，面积为2cm 2的△ABC ，沿BC 方向平移至△DEF 的位置，平移的距离是边BC 长的2倍，则图中的四边形ACED 的面积为（ ）A ．4cm 2B ．6cm 2C ．8cm 2D ．10cm 28、如图所示，三张正方形纸片①，②，③分别放置于长()a b +，宽()a c +的长方形中，正方形①，②，③的边长分别为a ，b ，c ，且a b c >>，则阴影部分周长为（ ）A ．42a c +B ．42a b +C ．4aD ．422a b c ++9、经过平移，ABC ∆移到DEF ∆的位置，如图，下列结论：①AD BE CF ==，且////AD BE CF ；②//AB DE ，//BC EF ，BC EF =；③AB DE =，BC EF =，AC DF =．正确的有( )A ．0个B ．1个C ．2个D ．3个10、如图，将△ABC 沿直线AB 向右平移后到达△BDE 的位置，连接CD 、CE ，若△ACD 的面积为6，则△BCE 的面积为（ ）A ．5B ．6C ．10D ．3二.填空题（共 8 小题）1、在平面直角坐标系中，将点（3，﹣2）先向右平移2个单位长度，再向上平移3个单位长度，则所得点的坐标是_____．2、如图，△ABC 的面积为10，BC ＝4，现将△ABC 沿着射线BC 平移a 个单位（a ＞0），得到新的△A'B'C'，则△ABC 所扫过的面积为_____．3、如图，将直角△ABC 沿斜边AC 的方向平移到△DEF 的位置，DE 交BC 于点G ，BG=4，EF=10，则线段GC 的长 ______________．4、如图，若DEF ∆是由ABC ∆平移后得到的，已知点A 、D 之间的距离为1，2CE =，则BC =_______．5、如图，O 是正六边形ABCDEF 的中心，下列图形：△OCD ，△ODE ，△OEF ，△OAF ，△OAB ，其中可由△OBC 平移得到的有_________个．6、如图所示是一座楼房的楼梯，高1 m ，水平距离是2.8 m ．如果要在台阶上铺一种地毯，那么至少要买这种地毯________7、如图，在长为50米，宽为30米的长方形地块上，有纵横交错的几条小路，宽均为1米，其它部分均种植花草．则种植花草的面积______．8、如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C 的方向平移到△DEF的位置，AB ＝10，DO ＝4，平移距离为6，则阴影部分面积为__三.解答题（共 6 小题）1、如图，平面内点A ，B 沿同一方向，平移相同距离分别得到点C ，D ，连接AB ，BC ，延长AC 到点E ，连接BE ，DE ，BC 恰好平分∠ABE ．(1)若∠ACB ＝100°，∠CBE ＝40°，求∠EBD 的度数；(2)若∠AED ＝∠ABC+∠EBD ，求证：BC//DE ．2、（1）动手操作如图1，在55⨯的网格中，将线段AB 向右平移，得到线段A B ''，连接AA '，BB '． ①线段AB 平移的距离是_________；②四边形ABB A ''的面积_________；（2）如图2，在55⨯的网格中，将折线ACB 向右平移3个单位长度，得到折线AC B '''．①画出平移后的折线AC B '''；②连接AA '，BB '，多边形ACBB C A '''的面积_________；（3）拓展延伸如图3，在一块长为a 米，宽为b 米的长方形草坪上，修建一条宽为m 米的小路（小路宽度处处相同），直接写出剩下的草坪面积_________．3、如图，在方格纸内将三角形ABC 经过平移后得到三角形111A B C ，图中标出了点A 的对应点1A ，解答下列问题．(1)在网格中画出三角形.111A B C .；(2)连接，1AA ，1BB ，则所得正方形.11AA B B .的面积是______，它的边长AB 是______．4、如图，在66⨯的正方形网格中，每个小正方形的边长为1，点A ，B ，C ，D ，E ，F ，P 均为格点（格点是指每个小正方形的顶点），请完成下列问题：(1)利用直尺画图：在图1中，过P 点画直线AB 的平行线和垂线；(2)平移图2中的三条线段AB 、CD 、EF 中的两条，使平移后三条线段首尾顺次相接组成一个三角形；（只画出一个三角形即可）(3)图2中所组成的三角形的面积为______．5、画图并填空：如图，在12⨯8 的方格纸中，每个小正方形的边长都为1 ，△ABC 的顶点都在方格纸的格点上，将△ABC 按照某方向经过一次平移后得到△A' B'C ' ，图中标出了点C 的对应点C ' ．（1）请画出△A' B'C ' ；（2）利用方格纸，在△ABC 中画出AC 边上的中线BD 和BC 边上的高AE ；（3）点F 为方格纸上的格点（异于点B ），若S ∆ACB = S ∆ACF ，则图中格点F 共有 个．（请在方格纸中标出点F ）6、平移和轴对称是数学中两种重要的图形运动．(1)平移①把笔尖放在数轴的原点处，先向负方向移动5个单位长度，再向正方向移动2个单位长度，这时笔尖的位置表示什么数？用算式表示以上过程及结果是（ ）．A ．(5)(2)7+++=+B ．(5)(2)3++-=+C ．(5)(2)3-++=-D ．(5)(2)7-+-=-②一机器人从原点O 开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳，当它跳2022次时，落在数轴上的点表示的数是________．(2)轴对称若对折纸条，表示-1的点与表示3的点重合，则表示2022的点与表示________的点重合．(3)若数轴上M ，N 两点对应的数分别表示为m ，n ，将点M 向正方向平移5个单位得到1M ，将点N 向负方向平移3个单位长度得到1N ，且1M ，1N 两点经对折后重合，对折的中间点表示的数为多少？（用含有m ，n 的式子表示）。

5.4平移数学教案
标题：五年级数学课——平面图形的平移
一、教学目标：
1. 学生能理解并描述什么是平移。

2. 学生能运用平移知识解决实际问题。

3. 学生能通过实践操作，提高空间想象能力。

二、教学重点和难点：
重点：理解和掌握平移的概念及性质。

难点：应用平移知识解决实际问题。

三、教学过程：
（一）导入新课
利用多媒体展示生活中的平移现象，如电梯的上下移动，汽车的前进等，引导学生观察并提问：“这些物体是如何运动的？”，引出“平移”概念。

（二）讲授新课
1. 定义平移：平移是物体或图形沿着直线方向移动，不改变形状和大小。

2. 平移的要素：方向和平移距离。

3. 平移的特点：形状、大小不变，位置改变。

4. 实践操作：让学生用纸片制作简单的图形，然后进行平移操作，体验平移的过程。

（三）课堂练习
设计一系列与平移相关的习题，包括判断哪些是平移现象，计算平移的距离，以及在方格纸上画出平移后的图形等。

（四）总结提升
回顾本节课的主要内容，强调平移的特点和应用，并鼓励学生在生活中寻找平移的现象。

四、课后作业
设计一些开放性的问题，如：“你能找到生活中有哪些平移的例子？”、“如果你是一个建筑师，你会如何运用平移的知识来设计建筑？”等，以培养学生的创新思维和解决问题的能力。

五、教学反思
记录教学过程中的成功和不足之处，以便于下次教学时改进。

《平移》教学案例教学内容：平移的概念和基本操作教学目标：1.理解平移的概念和基本操作；2.掌握平移的技巧和方法；3.运用平移概念解决实际问题；教学重点：1.平移的定义和基本操作；2.平移与图像的关系；教学难点：1.运用平移解决实际问题；2.平移与图像的理解；教学方法：1.演示法；2.讨论法；3.实践操作；教学准备：1.平移相关的教学素材；2.用于实践操作的物体；教学步骤：第一步：导入新知（10分钟）介绍平移的概念，引出平移的基本操作。

通过实物和图片的对比，让学生理解平移是指在给定条件下保持形状不变的情况下，将一个图形整体沿着指定方向移动一定距离。

第二步：介绍平移的基本操作（10分钟）1.教师示范平移的基本操作。

教师拿一张纸板或者一本书，先在黑板上绘制一个图形作为初始位置，然后将纸板或书整体向左或向右移动一定距离，再绘制新位置的图形。

学生根据演示理解平移的基本操作。

2.请学生讲述他们对平移的操作的理解，并与教师进行讨论。

第三步：练习平移的方法及技巧（15分钟）1.教师介绍平移的技巧和方法。

平移可以通过多种方式实现，如使用平行尺、量角器等工具，也可以通过观察规律推断出图形的新位置。

2.提供练习题，让学生尝试使用不同的方法进行平移练习，如平行尺实测法、规律推断法等。

鼓励学生多角度思考和实践，培养灵活运用平移方法的能力。

第四步：解决实际问题（15分钟）1.实际问题的引入。

例如，一些城市规划部门需要将公园的位置从A 点平移到B点，请学生根据给定条件进行平移定位。

2.学生小组合作，讨论和解决实际问题。

引导学生使用平移的方法和技巧，解决给定的实际问题。

鼓励学生在解决问题的过程中思考和讨论，提供互动交流的机会。

第五步：总结与拓展（10分钟）1.教师对平移的概念、基本操作、方法和技巧进行总结。

2.引导学生思考平移的应用领域，如建筑设计、工程规划等，并展示相关领域的实例。

鼓励学生拓展思维，思考平移在其他领域的可能性和应用。

《平移》教案五篇第一篇：《平移》教案《平移》教案教学目标：知识与技能：能在方格纸上按水平或垂直方向将简单图形平移。

过程与方法：通过观察、操作等活动，在方格纸上进一步认识图形的平移，并体会平移运动的特点。

情感与态度：在画图活动中，培养学生的合作意识，发展空间观念，并感受图形的美。

教学重点：能按要求画出简单的平面图形平移后的图形；会根据平移前后的图形判断平移方向和距离。

教学难点：认识图形的平移变换，探索它的基本性质，建立直观的空间观念。

教学方法：讲授法、谈话法课前准备：课件课时安排：1课时教学过程：创设情境，揭示课题1．播放“五星红旗升起”的视频。

在2008年北京奥运会乒乓球男子单打项目中，冠军是马琳，亚军是王皓，季军是王励勤，为中国一起得了三块奖牌，让我们一起来看视频，感受五星红旗冉冉升起的场面。

2．感知平移运动的方式。

五星红旗是怎么运动的？请大家用手势模仿它们的运动方式。

这种运动方式就是我们三年级学过的平移，你能举几个生活中平移的例子吗？3．揭示课题。

这节课我们将继续学习习近平移。

（板书课题：平移）设计意图：创设情境，把鲜活的生活情境引入课堂，让学生置身其中，唤醒学生的生活经验，激发学生学习数学的欲望。

探究新知，建构模型1.探究画水平方向平移后的图形的方法。

（1）出示教材25页的第一个问题。

题中给我们提出了什么要求？在画小旗向左平移4格后的图形时，先考虑哪个条件？如何画小旗向左平移4格后的图形？(引导学生讨论、汇报自己的想法)我们画出平移后的图形，所有的对应点都应满足向左平移4格的要求。

（2）学生试着画出小旗向左平移4格后的图形。

（3）教师巡视，找出学生的典型错例，学生可能会出现的错误：①平移的方向不对。

②平移后的图形形状或大小与原图形不符。

（4）引导学生讨论发现：把小旗向左平移4格，先要确定平移的方向，可以画个小箭头代表向左平移，再找到图形中的关键点(小旗四个顶点和旗杆下方的点)，然后把关键点先平移相应的格数，最后连点成线，画出与原图形相同的图形。

人教版数学七年级下册《5-4平移》教案一. 教材分析《5-4平移》是人教版数学七年级下册的一章内容，主要向学生介绍平移的性质和应用。

本节课的内容是学生学习几何图形变换的重要基础，也是进一步学习旋转、对称等变换内容的前提。

通过学习平移，学生能够理解图形的平移规律，掌握平移的性质，并能运用平移解决实际问题。

二. 学情分析七年级的学生已经具备了一定的几何图形知识，但对平移的概念和性质可能还比较陌生。

学生在学习本节课时，需要通过实例观察和操作实践，来理解和掌握平移的性质。

此外，学生可能对平移在实际问题中的应用还不够了解，需要通过具体的案例和练习来培养运用能力。

三. 教学目标1.了解平移的概念，掌握平移的性质。

2.能够运用平移的性质解决实际问题。

3.培养学生的观察能力、操作能力和运用能力。

四. 教学重难点1.平移的概念和性质。

2.运用平移解决实际问题。

五. 教学方法1.实例观察：通过具体的图形实例，让学生观察和分析平移的性质。

2.操作实践：让学生亲自动手进行图形平移的操作，加深对平移的理解。

3.问题解决：引导学生运用平移的性质解决实际问题，培养学生的运用能力。

六. 教学准备1.教学课件：准备相关的教学课件，用于展示图形实例和问题解决。

2.练习题：准备一些练习题，用于巩固学生的学习效果。

七. 教学过程1.导入（5分钟）通过一个简单的图形平移实例，引导学生思考平移的性质，激发学生的学习兴趣。

2.呈现（10分钟）展示一些图形平移的实例，让学生观察和分析平移的性质，引导学生进行思考和讨论。

3.操练（10分钟）让学生亲自动手进行图形平移的操作，加深对平移的理解。

教师可以给予适当的指导和建议。

4.巩固（10分钟）给出一些练习题，让学生运用平移的性质进行解答。

教师可以给予学生适当的帮助和指导。

5.拓展（10分钟）给出一些实际问题，引导学生运用平移的性质进行解决。

教师可以给予学生适当的提示和指导。

6.小结（5分钟）对本节课的内容进行简要回顾和总结，强调平移的概念和性质，以及运用平移解决实际问题的重要性。

平移问题平移性质——平移前后图形全等，对应点连线平行且相等。

一、直线的平移1、(2009武汉)如图，直线43y x =与双曲线k y x =（0x >）交于点A ．将直线43y x =向右平移92个单位后，与双曲线k y x =（0x >）交于点B ，与x 轴交于点C ，若2=BC AO ，则k = ．2、（09年四川南充市）如图已知正比例函数和反比例函数的图象都经过点(33)A ，．（1）求正比例函数和反比例函数的解析式；（2）把直线O A 向下平移后与反比例函数的图象交于点(6)B m ，，求m 的值和这个一次函数的解析式；（3）第（2）问中的一次函数的图象与x 轴、y 轴分别交于C 、D ，求过A 、B 、D 三点的二次函数的解析式；（4）在第（3）问的条件下，二次函数的图象上是否存在点E ，使四边形O ECD 的面积1S 与四边形O ABD 的面积S 满足：123S S =？若存在，求点E 的坐标；若不存在，请说明理由．提示:第（2）问，直线平行时，解析式中k 值相等。

3、（2009年日照）某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD 是矩形，其中AB =2米，BC =1米；上部CDG 是等边三角形，固定点E 为AB 的中点．△EMN 是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN 是可以沿设施边框上下滑动且始终保持和AB 平行的伸缩横杆．（1）当MN 和AB 之间的距离为0.5米时，求此时△EMN 的面积；（2）设MN 与AB 之间的距离为x 米，试将△EMN 的面积S （平方米）表示成关于x 的函数；FA D EB F C图4（备） A D E B F C 图5（备） A D E B F C 图1 图2 A D E B F C P N M 图3 A D EB FC P N M （第25题）提示：第（2）问，按MN 分别在三角形、矩形区域内滑动分类讨论；第（3）问，对（2）问中两种情况分别求最值，再比较得最值。